基于相电流重构的永磁同步电动机直接转矩控制
胡云飞,黄守道,刘 坚,徐振宇
(湖南大学,湖南长沙410082)
0 引 言
三相电压型PWM逆变器广泛应用于工业领域,如交流电机驱动系统和不间断电源等,在这些应用中都需要相电流控制。在变频器高性能控制方案中,电流采样性能是其中一个关键环节,往往直接影响到整个控制方案性能的好坏。目前较常采用的电流采样方法有:使用两个电流霍尔传感器采样电机两相相电流[1];采用单个霍尔传感器采样正、负直流母线电流的方法进行电流重构[2]。上述两种方法虽具有使用简单、电气隔离的显著优点,但价格高昂、体积庞大。
在本文中,对基于相电流重构的永磁同步电动机直接转矩空间矢量控制进行了描述,定子磁通矢量和电磁转矩直接从α和β的电压和电流瞬时空间矢量计算得到。相电流重构分两个过程:基于动态电机模型的相电流预测过程和基于逆变器开关状态的相电流调整过程,且直接依赖直流电流测量值。
1 相电流重构基本原理
在逆变器三个桥臂运行期间,有六个有效矢量和两个零矢量,当任何一个有效电压矢量运行时,三个相电流中的一相就会出现在直流侧,当开关状态为Sabc=100(Sabc为上桥臂的开关状态,1为开,0为关,上下桥臂不能同时为开)时,如图1所示,相电流和母线电流的关系为ia=idc,其他矢量作用时,相电流和母线电流之间的一一对应关系如表1 所示[3]。

图1 Sabc=100时的电流流向图

表1 相电流和直流侧电流的关系
由以上理论可以得出,在逆变器开关状态改变时只需采样母线电流,就可以重构出相电流。
2 基于动态电机模型的相电流重构
基于动态电机模型相电流重构分两部分:首先,从动态电机模型中提取电流模型,将值作为相电流预测值;然后,利用测量得到的直流电流值来调整其他两相的相电流预测值。
永磁同步电动机电压方程如下:

式中:Eα、Eβ是电机的反电势,由电机转速ωr和位置角θ计算得来,如下:
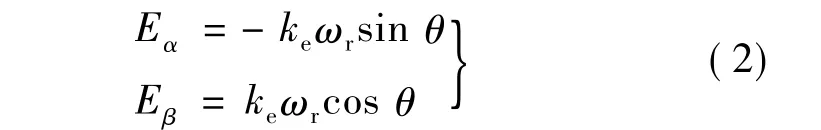
ke为反电势常数,也可实验得到。
求解式(1)可得到电流iα和iβ的值:

对上式进行离散化,结果如下:

式中:Ts表示采样时间,k-1表示前一次采样值,iα(k)、iβ(k)表示现在估计的电流值。从上式可以看出,相电流的重构与不仅与前一次采样得到的相电流有关,还与前次采样的相电压、反电势有关。相电压采样由电压传感器完成,反电势采样由式(2)得到。
由式(4)得到的αβ轴相电流经Clarke反变换,变换到abc三相静止坐标系。将测量值与预测值相比较得到差值,用差值的一半来补偿其他两相预测电流值。以a相为例,如果某一时刻根据开头状态,从直流侧得到的是a相电流测量值,设为iam,由式(4)得到a相电流预测值,设为iap,ia为a相重构值[4-5],此时令:

测量电流与预测电流的差值:

另两相电流:

当从直流侧得到的是其他相电流时重构补偿,依此类推,由此便得到完整的三相重构电流。
3 直接转矩控制
本文采用空间矢量调制(SVM)的直接转矩控制。采用SVM的目标是利用逆变器固有的基本空间电压矢量合成所需的参考电压空间矢量。传统的直接转矩控制中,只有6个有效的电压矢量和两个零矢量。这8个矢量称为基本空间矢量,它们把复平面分成6个扇区。SVM技术就是将根据磁链和转矩误差得到的目标电压矢量,用这6个基本电压矢量和两个零电压矢量中相应的矢量电压来合成。
永磁同步电动机转矩的产生受定子磁场的φs和永磁磁场φf之间相互作用,这两个磁场在αβ轴上的关系如图2所示。两磁场向量之间的夹角为δ,又叫负载角。在稳态时,永磁磁场同步旋转且δ为常数。对于瞬态工况如起动、突加载或给定速度突然发生变化的情况,磁链旋转速度将会发生变化,负载角也会发生改变,相应地转矩发生改变[6]。
定子磁链空间矢量的瞬时值可直接从定子反电势计算出来,如下:

图2 磁链矢量图

或者用它们的α和β分量:

忽略定子电阻压降,并转换成增量模式,我们可以得到:

方程显示,任何磁通矢量的变化都正比于定子电压矢量的幅值和方向。另外,任何定子磁通矢量角速度的变化都将影响到电磁转矩。例如,如果φs逆时针旋转且位于第二扇区,我们可以利用电压矢量V3和V4的作用时间长短来相应地增加和降低φs的大小,同时转矩会相应发生变化。一般来说,当φs在第k个扇区,我们可以用有效电压矢量k+1,k+2,k-1,k-2来控制磁链和转矩的大小,如图3所示。

图3 有效电压矢量分布
从α和β定子磁链和定子的电流分量可以计算出电磁转矩:

式中:p为电机的极对数。
将相电流模块加入直接转矩控制模型中,即可实现永磁同步电动机直接转矩相电流重构。图4为基于相电流重构的永磁同步电动机直接转矩控制的控制框图。
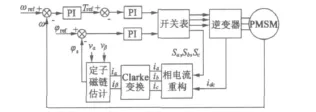
图4 基于电流重构的PMSM直接转矩控制框图
4 仿真分析
利用MATLAB/Simulink搭建图4的仿真模型,所选电机参数如表2所示。

表2 仿真所用电机参数
其中,仿真时间为0.5 s。转速给定为分别2 000 rad/s和1 000 rad/s时,空载起动,且在转速达到给定值稳定之后,分别在0.15 s和0.3 s时加载3 N·m和7 N·m,得到的仿真图形如图5、图6、图7、图8所示。



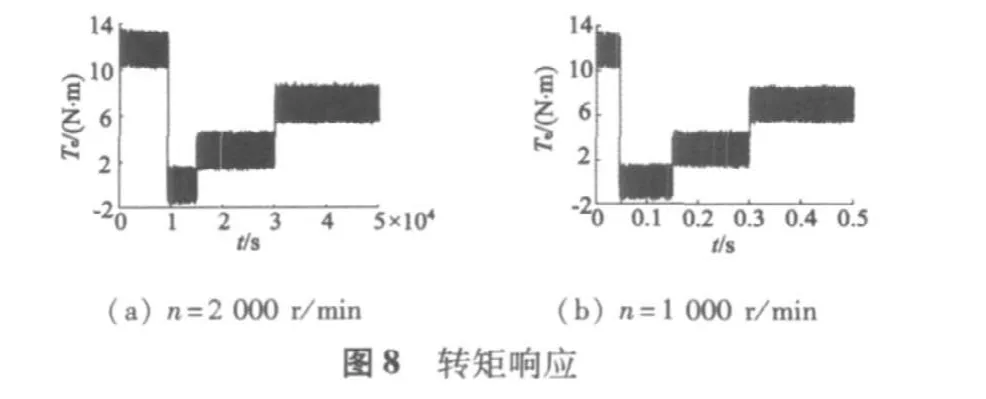
为分析方便,以a相电流为例,当给定转速为2 000 r/min时,如图5所示,当电机稳定运行后,重构电流与实测电流保持了良好的一致性,只出现极小的误差,这种误差在一般的PMSM控制系统中属于允许范围。当给定转速为1 000 r/min时,如图6所示,实测电流和重构电流基本保持一致,但是电流纹波比2 000 r/min时稍大,但依然在系统的承受范围之内。图6和图7分别为转速和转矩响应,从对比图看出,当给定转速和转矩发生变化,系统都有很好的跟踪特性。
当然,从以上几个图中也可以看出本重构方法的不足之处:(1)电机起动时,起动电流波动较大,有可能会造成过流;(2)当速度降低时,电流纹波加大,造成电机功耗增加,电流利用率有所下降。
5 结 语
本文对三相电压源型逆变器相电流的重构问题和空间矢量直接转矩控制进行了研究分析,提出了永磁同步电动机动态模型和开关状态相结合的永磁电机相电流重构方法,该方法根据永磁电机动态方程和不同开关状态下直流侧所代表的相电流不同,对三相交流电流进行了重构。仿真实验结果表明电流重构效果较好,既减小了系统体积,有效降低了成本,又提高了系统可靠性。但也有一些不足之处,如起动电流波动大等问题还需作进一步研究。
[1] 姜淑忠,李小海.电机驱动器中的电流传感器[J].电机与控制应用,2007,34(6):29-32.
[2] Blaabjerg F,Pedersen J K,Jaeger U,et al.Single current sensor technique in the DC link ofthree-phase PWM-VS inverters:a review and a novelsolution[J].IEEE Transactions on Industry Applications,1997,33(5):1241 -1253.
[3] 刘艳,邵诚.三相电压源型PWM逆变器相电流重构策略研究[J].信息与控制,2007,36(4):506 -513.
[4] Peralta- Sanchez E,Al- rifai F,Schofield N.Direct Torque Control of Permanent Magnet Motors Using a Single Current Sensor[J].IEEE Transactions on Industry Applications,2009,16:89 -94.
[5] Bertoluzzo M,Buja G.Direct Torque Control of an Induction MotorUsing a Single Current Sensor[J].IEEE Transactions on Industrial Electronics,2006,53(3):778 -784.
[6] 田淳,胡育文.永磁同步电机直接转矩控制系统理论及控制方案的研究[J].电工技术学报,2002(2):8-11.

