基于反馈线性化的风轮机变桨距控制研究

纪志成，冯海英，沈艳霞

(江南大学，江苏无锡214122)

0 引 言

风能是一种有效的清洁能源，随着能量需求的日益增加，风机容量日益扩大，变速恒频风力发电机组的研究已成为国内外相关领域的研究热点［1－2］。

早期主要研究低风速下风力机的控制策略及运行目标:低于额定风速运行时，风轮应跟踪最佳叶尖速比，实现风能的最大功率动态跟踪;高于额定风速时，采用变桨控制策略，将转速恒定在额定值附近并维持输出功率稳定。然而，风速波动范围较宽，空气的气动力特性，随机机械阻尼的影响以及柔性结构的传动链等因素是系统控制困难的原因［3］。

文献［4］以变桨控制为目标，通过反馈控制器观察转速信号，设计了鲁棒控制器;文献［5］用神经网络法对风电系统进行进一步分析控制，对比了MLP和RBF神经网络的控制特性;文献［6］提出了变速恒频风力发电转速非线性PID控制，它具有一定的适应性和鲁棒性;文献［7］提出模糊PI变桨距控制法，并与变增益法和基于机械转矩观测器的控制增益法等控制方案进行了比较分析;此外，自适应控制、模糊神经网络、变论域自适应、灰色预测、数据驱动等先进控制方法也是常用的变桨距控制方法［8－10］。

由于风能的气动效应及随机性等特点，传统的控制方法已难于实现高精度控制，并且输出电能质量较差。为了改善系统在高于额定风速运行区域内的动态性能，变速恒频风力发电已成为一种主导趋势，该系统具有强非线性、动态过程较快等特点。本文根据风力发电机组的模型，将风轮机模型进行精确反馈线性化，并设计最优控制器，通过仿真得到波形，对比开环性能，论证了浆距角控制的重要性，并对改变参数进行了比较分析。

1 风力发电机组模型

1.1 风轮机模型

风轮机从自然风能中吸取能量的大小程度用风能利用系数Cp来表示［11］:

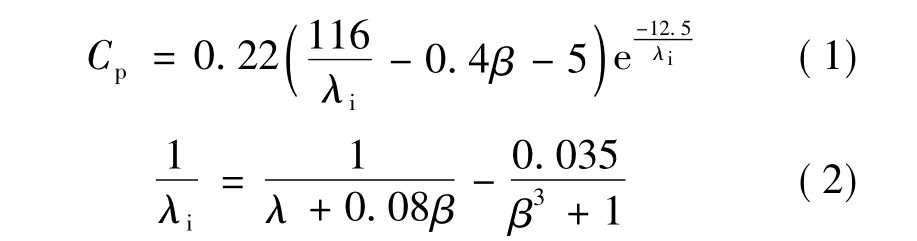
作为风力机组的关键部件的一部分，风轮机将桨叶捕获的风能转换为传递到轮毂上的机械转矩。其动态方程:

式中:Tgen为发电机的电磁转矩，为便于分析，本文设为定值;J为风轮转动惯量;Taero为风给的风轮动力矩，为整个机组的驱动力矩;Taero可表示:

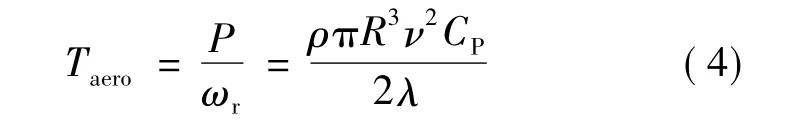
式中:P为风轮机实际获得的轴功率。

不同于额定风速以下采用的最大叶尖速跟踪调节，额定风速以上时，系统主要采用变桨距调节这一复杂动态过程，将系统输出功率保持在额定值附近。为便于分析，本文采用直驱式传动系统。

1.2 桨距角的执行机构

桨距角的执行机构为一阶惯性环节:

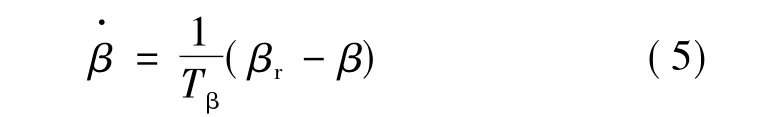
式中:Tβ为变桨伺服系统的时间常数;β是执行机构的输出，即桨距角的实际值;βr为参考桨距角，是控制器输出的给定值。一般来讲，Tβ很小，β可以很快跟踪到βr。

1.3 测速装置

由于存在滞后，用一个一阶惯性环节来表示:

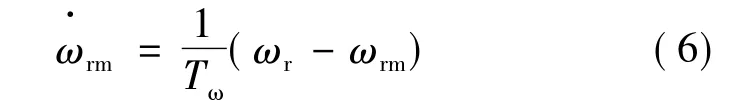
式中:ωrm是利用速度传感器得到的风力机角速度;Tω为系统的时间常数。

1.4 全局模型

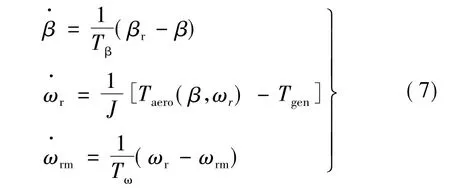
由以上分析可得，该系统是三阶的，状态变量有测量转速ωrm、风轮机转速ωr、桨距角β。

2 基于精确反馈线性化的变桨距控制器设计

2.1 精确反馈线性化

所谓状态反馈线性化［12－13］，就是在一定条件下，将一个仿射非线性系统通过非线性状态反馈和恰当的坐标变换进行精确线性化，用得到的状态反馈维持控制系统的平稳性，提高系统的动态性能。由于它精确对消了系统的非线性特性，该方法又被称作精确反馈线性化。

状态反馈线性化可应用于如式(8)的单输入单输出仿射非线性系统:

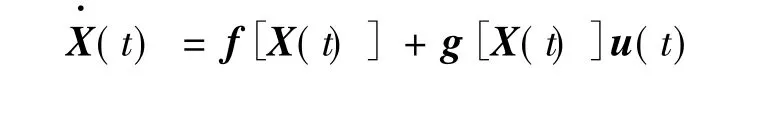
式中:f(X)及g(X)为状态空间中n维向量场;u∈Rl为控制量;X∈Rn为状态向量;h(X)为X的标量函数;y∈Rl为输出量。

2.2 线性二次型最优控制

对于线性控制系统:

式中:A和B分别为n×n维状态系数矩阵与n×m维控制系数矩阵，Z为n维状态向量，V为m维控制向量，若矩阵［B|AB|A2B|…|An－1B］的秩为 n，则式(9)完全可控。对其提出二次型目标函数:

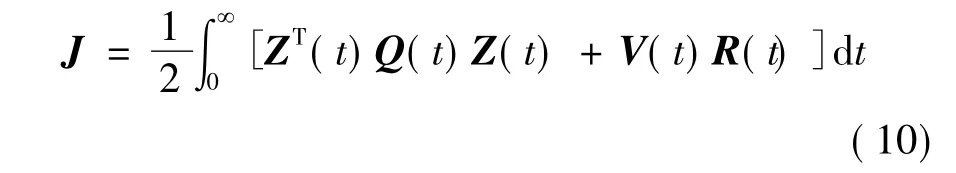
式中:R为正定m×m阶权矩阵;Q为非负定n×n阶权矩阵。由线性控制理论［14］得式(9)的最优控制V(t)*:

的解。

利用Matlab 7函数“care()”求解代数黎卡提(Riccati)方程，使用方法如下:

式中:L是闭环状态方程参数矩阵的特征值;P是求得的代数黎卡提方程的解;K为最优反馈增益矩阵。

2.3 风力机组模型的精确反馈线性化和最优控制器设计

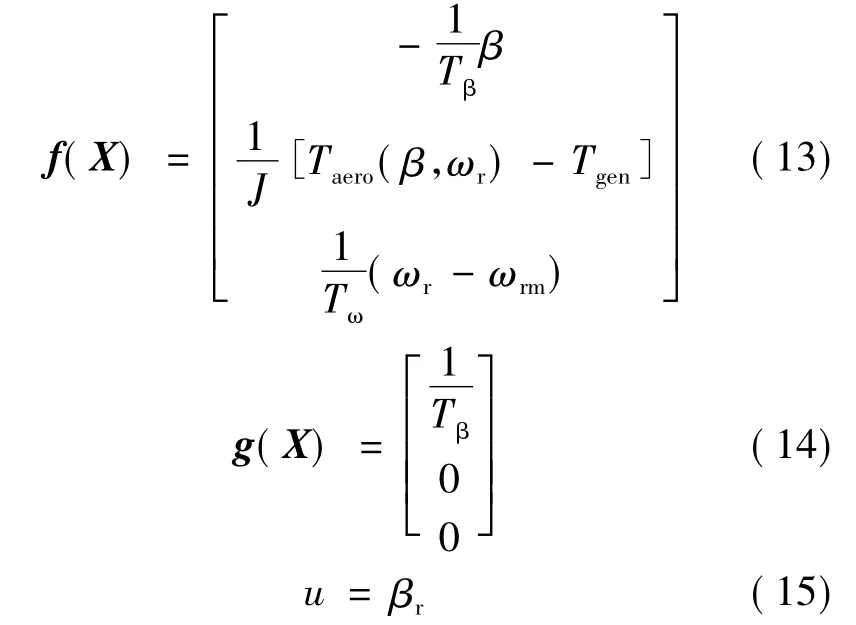
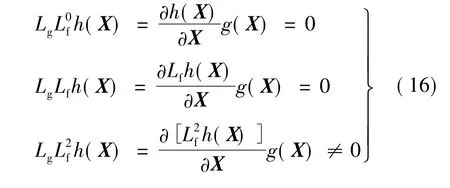
所以此系统的r=3，满足进行精确反馈线性化变换的条件。

第二、选取合适的状态反馈及变换坐标。令φ:

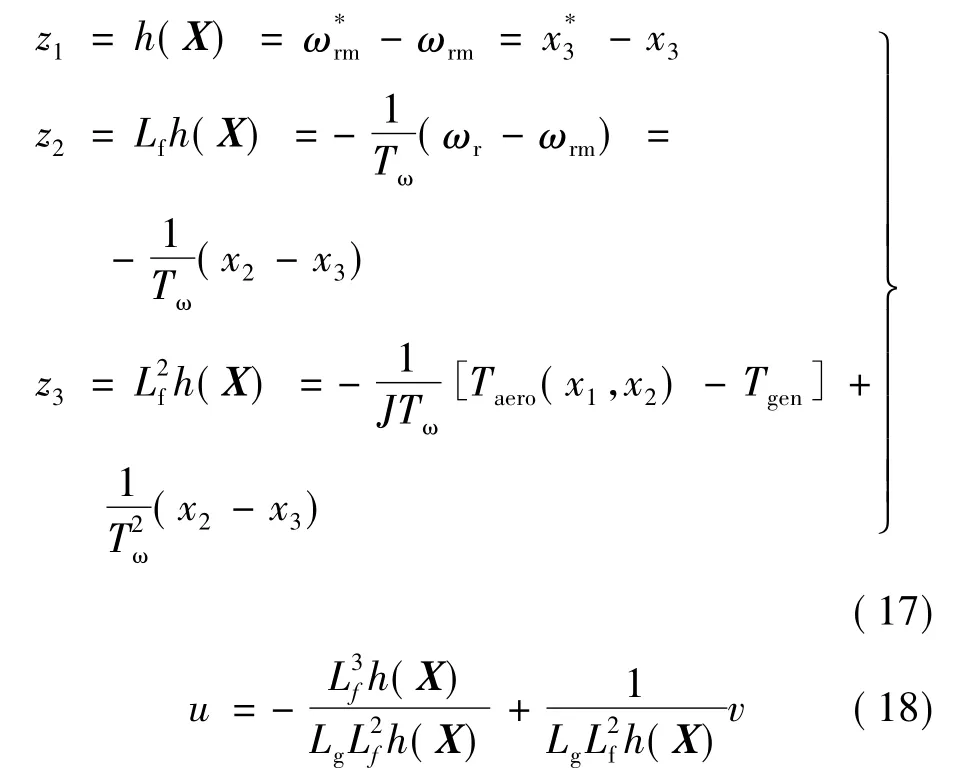
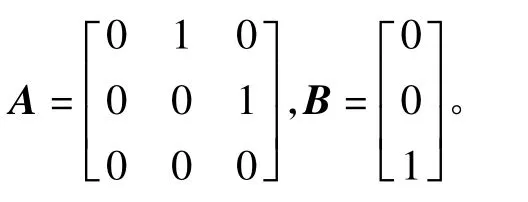
由式(18)可以看出，一旦v确定，控制量u也随之确定，即βr确定，最优控制器为确定v提供了途径。

用控制器输出的控制量来使性能指标J达最小并保持较小的系统误差是最优控制的目的，从而实现能量和误差的统筹最优控制。因此使控制向量V:

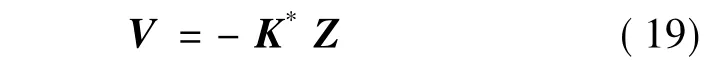
此处，K*为最优反馈增益矩阵，且有:

选取 R=1，Q=diag(500，500，0)，由式(11)和式(20)用Matlab求解出:

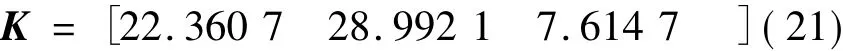
结合式(19)得线性系统最优控制量v:

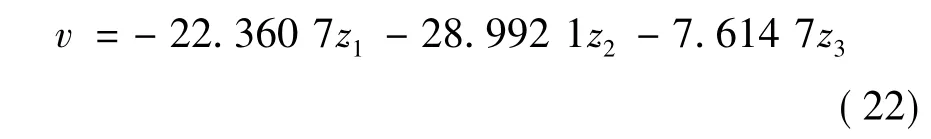
结合式(18)，可得所建的三阶线性模型的状态反馈控制律为:

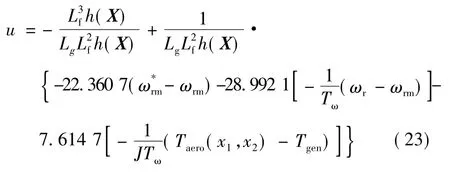
3 系统仿真与分析

为了验证本文所设计的精确反馈线性化和最优控制器系统的正确性，本文用两种风速模拟并对风电机组进行开环仿真。风力发电机组的主要仿真参数如表1所示。

表1 仿真参数表

在不同风速下，输出功率和风轮转速的开环仿真结果如图1和图2所示。

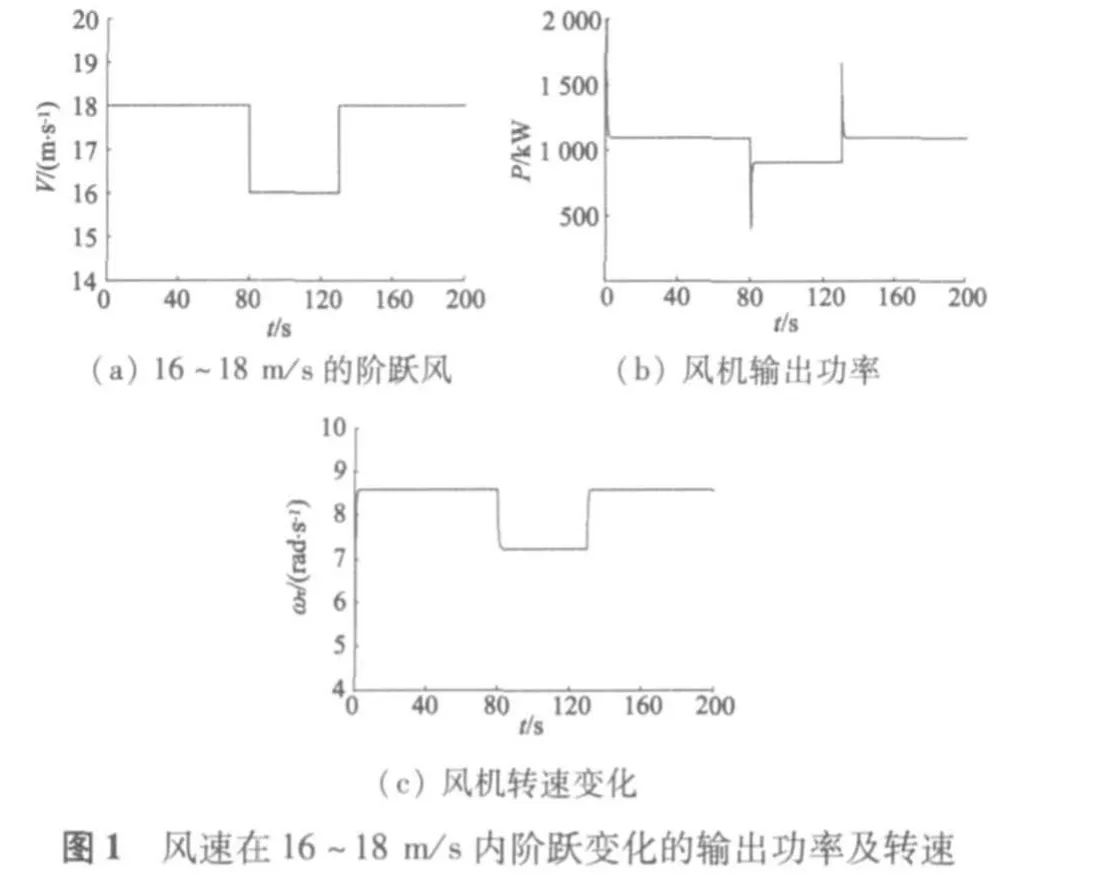
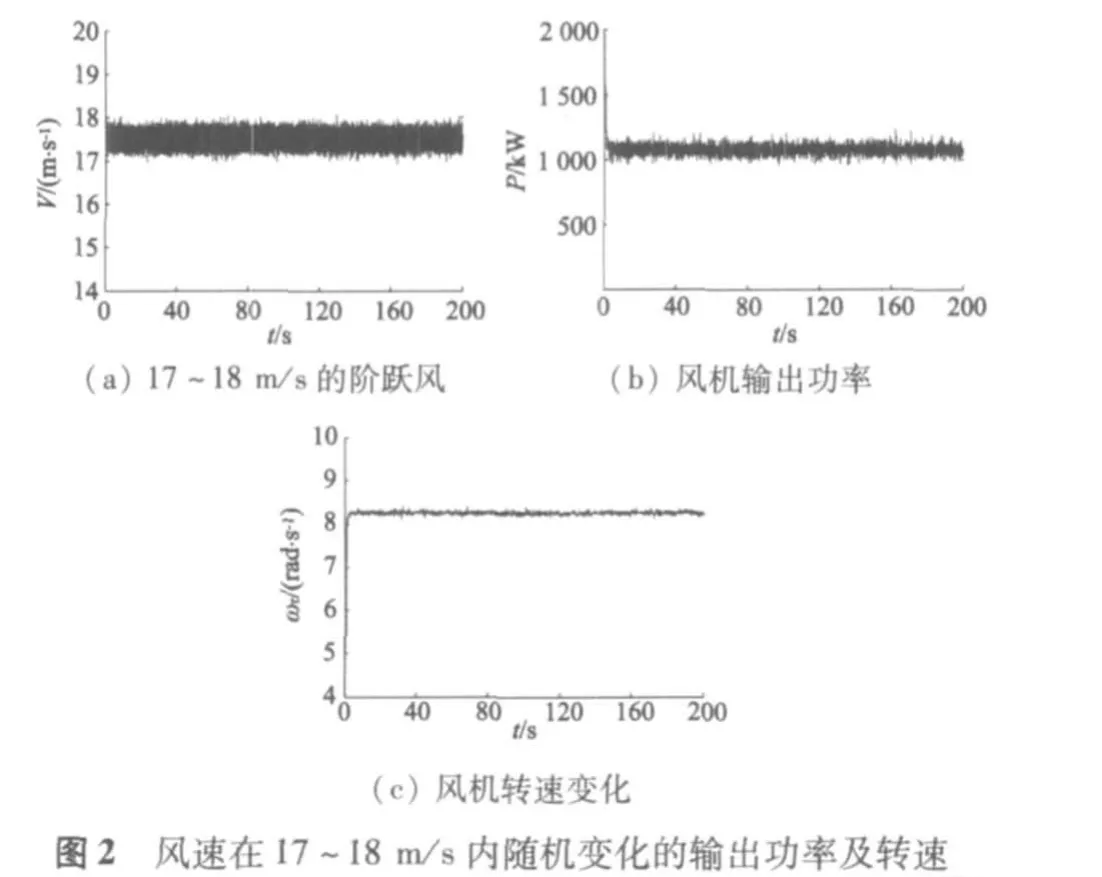
通过对上述结果的分析知道，当风电系统为开环控制时，其输出功率和转速难以保持在额定值附近，因此一个合适的控制器是必须的，只有风力机的输出功率保持在允许范围内，发电机的恒定功率输出才能实现。因此，额定风速以上时的变桨距控制成为直驱型风力发电系统的关键。

基于精确反馈线性化和最优控制器的闭环仿真结果如图3和图4所示。

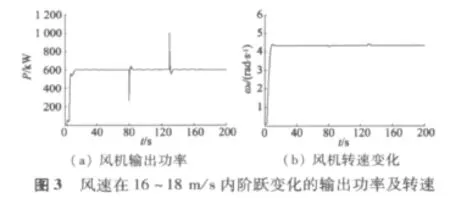
由图3知，当风速在80 s处由18 m/s跳变到16 m/s时，风力机转速由4.34 rad/s迅速变为4.27 rad/s，相应的输出功率也变小，为防止其偏离额定值，变桨控制器动作，使输出功率迅速回升至额定值;而当风速在130 s处回升至18 m/s时，为使风能利用率减小，桨距角调节，依然将输出功率保持在额定值附近。

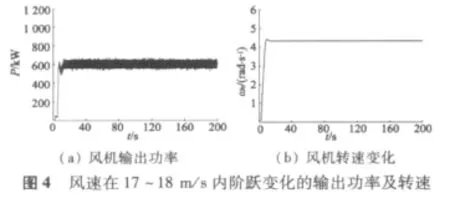
由图4可得，当风速模型为随机风时，由于桨矩角控制器的及时调节，改变风能的功率系数，从而风力机的输出功率被限定在允许的范围内，并使转速维持在额定值附近。但须指出的是，该控制策略在起始阶段响应较慢，稳定性不够好，这是有待进一步研究的内容。

4 结 语

为提高变速恒频风力发电机组额定风速以上的控制性能，本文在分析风电机组不同风速模型开环仿真结果的基础上，提出反馈线性化的风轮机变桨距控制方案，结合最优控制器，从而使风机功率和转速值维持在额定值附近。仿真波形证明该控制方法对风速和系统参数具有很好的鲁棒性，并且具有较好的动态性能。

［1］ 马幼捷，尹向前，赵国华，等.变速恒频双馈风电机组参数扰动对并网控制的影响［J］.太阳能学报，2009，30(5):650 －654.

［2］ Beltran B.Ahmed－Ali T.Sliding mode power control of variable－ speed wind energy conversion system［J］.IEEE Transactions on Energy Conversion，2008，23(2):551 －558.

［3］ Senjyu T，Sakamoto R，Urasaki N，et al.Output power leveling of wind turbine generator for all operating regions by pitch angle control［J］.IEEE Transactions on Energy Conversion，2006，21(2):467－475.

［4］ Takaai H，Chida Y，Sakurai K，et al.Pitch Angle Control of Wind Turbine Generator using Less Conservative Robust Control［J］.IEEE International Conference on Control Applications，2009，7(18):542－547.

［5］ Yilmaz A S，Ozer Z.Pitch angle control in wind turbines above the rated wind speed by multi－layer perceptron and radial basis function neural networks［J］.Expert Systems with Applications，2009(36):9767－9775.

［6］ 赵永祥，夏长亮，宋战锋，等.变速恒频风力发电系统风机转速非线性PID控制［J］.中国电机工程学报，2008，28(11):133－138.

［7］ Cardenas－ Dobson R，Asher G M.Power limitation in variable speed wind turbines using pitch control and mechanical torgue observer［J］.Wind Engineering，1996，20(6):363 －386.

［8］ 郭庆鼎，赵麟，郭洪澈.1MW变速变距风力发电机的滑模变结构鲁棒控制［J］.沈阳工业大学学报，2005，27(2):171 －174.

［9］ 刘新海，于书芳.神经网络在大型风力发电机电控系统中应用［J］.微特电机，2004，32(2):37 －42.

［10］ 张新房，徐大平，吕跃刚，等.大型变速风力发电机组的自适应模糊控制［J］.系统仿真学报，2004，16(3):573 －577.

［11］ 夏长亮，宋战锋.变速恒频风力发电系统变桨距自抗扰控制［J］.2007，27(14):91 －95.

［12］ 卢强，孙元章.电力系统非线性控制［M］.北京:科学出版社，1993，10 －60.

［13］ 贺昱曜，闫茂德.非线性控制理论及应用［M］.西安:西安电子科技大学出版社，2007，20 －36.

［14］ 胡寿松，王执铨，胡维礼.最优控制理论与系统［M］.北京:科学出版社，2005.