基于转子固有高频信号的同步电动机转子位置检测
黄 坤,庞晴晴,王 磊
(中国矿业大学,江苏徐州221008)
0 引 言
在高性能的同步电动机矢量控制系统中,需要准确地知道转子位置信息,而转子位置的检测一般通过光电编码器、旋转变压器等机械位置传感器来实现[1]。这些机械位置传感器的使用又会给调速系统带来不少问题:
(1)采用机械位置传感器需要添加额外的装置,这就大大增加了系统的投入成本;
(2)机械位置传感器需要安装在电机的轴上,同心度会影响安装的问题,安装不当将影响测速精度;
(3)机械位置传感器的安装加大了电机轴向上的体积,使电机结构变得较为复杂,降低了控制系统的机械鲁棒性;
(4)由于机械位置传感器本身受高温、高湿等恶劣环境的影响很大,因而使得系统的工作精度受到环境条件的影响[2];
(5)此外,机械位置传感器的使用还加大了系统运行和维护的难度。
为了弥补位置机械传感器的缺陷,自20世纪70年代起,越来越多的学者开始研究无机械位置传感器的辨识方法[3]。目前绝大部分无机械位置传感器研究都是针对永磁同步电动机或者是感应电动机,电励磁同步电动机的无传感器控制却很少提及。
本文针对电励磁同步电动机提出了一种新颖的无机械位置传感器的同步电动机转子位置检测方法,即转子侧注入高频信号的位置和速度检测方法,并且给出了一种转子侧注入高频信号的实现方法。该方法一方面简化同步电动机速度闭环控制系统的硬件结构,另一方面提高控制系统可靠性和实用性。
1 基于转子侧高频信号注入的位置检测原理
无传感器的检测原理即是利用同步电动机自身结构构成传感器,根据基本的电压和电流信号以及电机的电磁关系来计算电机位置和速度,达到取代外加的机械传感器的目的。
如图1所示,在电励磁同步电动机的转子上有一个转子绕组,定子上有三个对称分布的定子绕组,因此可以将电励磁同步电动机本身作为一个旋转变压器,转子绕组即为旋转变压器的输入绕组,定子绕组即为旋转变压器的输出绕组[4],在转子侧输入高频信号后,就可以在定子绕组中检测到相应的高频响应信号,进而计算出转子的位置[5]。该方法具体的工作原理分析如下。

图1 同步电动机转子位置测量原理图
当转子绕组中叠加角频率为ωH、有效值为UrH的高频励磁信号时,它会在转子N极轴线(即d轴)方向产生高频脉振磁场ΦrH=Φmsin(ωHt),该高频磁场幅值位置会随转子位置变化而移动[6]。设d轴与定子U相绕组相轴(即U轴)的空间夹角的电角度为θ,则该高频脉振磁场分别穿过定子三相绕组的磁通(如图1所示):
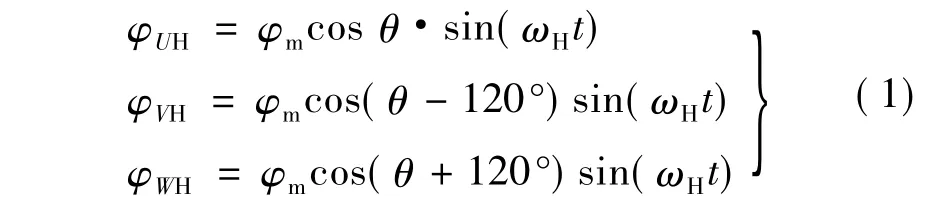
根据变压器原理可知,该高频脉振磁场分别在转子绕组和定子三相绕组感应的电势(如图1所示):
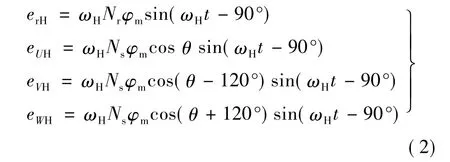

由于高频电流很小,所以对于漏抗压降相对高频感应电势来说仍然很小,可以忽略绕组漏阻抗。由式(2)可得出转子和定子绕组的高频电压有效值大小:

可见,定子三相高频电压的频率和相位与转子高频电压相同,但是有效值按照式(3)变化。
为了计算方便,将定子三相绕组输出电压折算到转子侧(即除以电压比),可以得到定子三相绕组输出电压折算值:

利用式(4),可以得出定子U相高频电压和VW高频线电压:

利用式(4)可以计算出转子位置。
利用上述方法判断出转子位置角度θ的区间后,再利用式(5)可以计算出转子位置角度θ的大小,即:

式(6)是利用定子U相高频电压和VW高频线电压的比值来计算,因此转子高频励磁电压幅值的大小不影响计算精度。
由于得到的转子位置角度θ为电角度,在考虑电角度与机械角度的关系后,对时间t的导数进行计算,即可得到转子的机械速度nr:
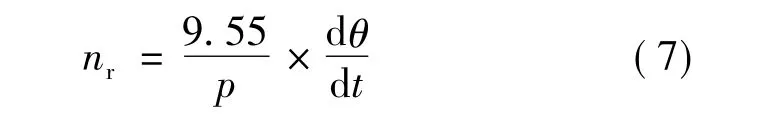
式中:p为电机的极对数。
2 无位置传感器矢量控制系统仿真
基于转子高频注入的同步电动机矢量控制系统框图如图2所示。系统中没有传统的机械位置传感器。同步电动机的定子绕组与定子功率变换器相连,同步电动机的转子绕组与转子功率变换器相连,在同步电动机转子绕组上注入一个高频电压励磁信号,利用电压互感器检测同步电动机定子绕组中含有高频成分的电压信号。将该电压信号通过信号滤波器进行滤波处理,即可得到转子的位置信号与电机的转速信号。将其送至系统控制器,系统控制器接收到从滤波器传来的转速反馈信号,将其与给定信号进行比较,从而发出控制信号,同时对定子功率变换器和转子功率变换器进行控制。两个功率变换器依据系统控制器所发出的控制信号改变其输出,从而实现快速准确地控制同步电动机的转速。

图2 基于转子高频的同步电动机控制系统图
为了验证本文提出的无传感器控制方法的正确性。在Matlab环境下建立了基于转子高频注入的同步电动机矢量控制系统仿真模型。仿真中选用的电励磁同步电动机参数:pN=16 kW;UN=400 V;Uf=12 V;fN=50 Hz;nN=1 500 r/min;Rs=0.645 Ω;Rf=0.396 8 Ω;Lmd=0.052 97 H;Lmq=0.025 18 H。
2.1 基于转子注入高频信号的转子位置检测
基于转子注入高频信号的转子位置检测即通过直接对转子注入高频电压信号的方法来对转子位置进行检测。仿真过程中,前1 s为电机转子励磁阶段,1 s时给定转速,电机起动,2 s时加入负载。注入的高频正弦电压的峰值为10 V,频率为1 kHz。高频正弦电压的注入时间为通入励磁电压0.1 s以后。
图3是转子位置观测的动态波形。图中依次为定子侧三相电流波形、定子侧感应的高频正弦电压、定子侧感应的高频余弦电压、解调得到的转子位置正余弦包络线、转子位置的实际值和观测值。从转子位置观测波形可以看出,转子侧高频注入之后,转子位置观测值很快跟随上实际值。

图3 基于转子注入高频信号的转子位置观测
2.2 基于转子固有高频信号的转子位置检测
由于电励磁同步电动机的转子绕组一般由三相可控整流桥供电(如图4所示),而三相可控整流桥输出的电压波形中含有丰富的高频谐波成分,因此可以利用这些高频谐波分量代替高频注入信号来对转子位置进行检测。在利用转子固有高频信号进行转子位置检测时,这里首先要对转子电压进行谐波分析。

图4 转子绕组供电的三相可控整流桥
图5为仿真中所用三相整流桥模块,即通过磁链调节器输出的电压计算得到三相可控整流桥的导通角,再输出相应的开关控制信号使得三相可控整流桥输出相应的电压。
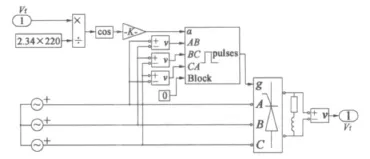
图5 三相可控整流桥模块
图6为由三相可控整流桥供电的转子电压波形,在过滤到低频基波成分后的谐波成分如图7所示可见,其中的300 Hz高频谐波信号量在所有谐波成分中是最大的,这是因为三相可控整流桥输出为一六脉动的电压信号,其中6 fs分量的谐波成分最为丰富,因此在fs=50 Hz时,300 Hz的分量最大。这里就采用转子电压波形中固有的300 Hz高频分量来进行转子位置检测。


图8为基于转子固有高频信号的转子位置检测过程。其中波形从上到下依次为定子侧三相电流波形、定子侧感应的高频正弦电压、定子侧感应的高频余弦电压、解调得到的转子位置正余弦包络线、转子位置的实际值和观测值。从转子位置观测波形可以看出,转子侧高频注入之后,转子位置观测值很快跟随上实际值。

图8 基于转子固有高频信号的转子位置观测
3 结 语
同步电动机矢量控制系统中的机械位置传感器存在安装困难、维护不方便和容易损坏等问题,无传感器控制技术是解决问题的根本途径。本文针对电励磁同步电动机的特殊结构和电磁特点,在提出了基于转子侧高频信号注入的转子位置角观测的无机械位置传感器方法的基础上,给出了一种转子侧注入高频信号的实现方法,即利用电励磁同步电动机转子三相可控整流桥输出电压中的固有高频信号来进行转子位置检测。本方法利用电励磁同步电动机的自身结构来检测转子位置信号,并通过自身绕组输出该信号,即在转子绕组中加高频励磁,定子绕组中就会感应与转子角度相关的高频信号,通过定子输出的该高频信号就可以计算出转子位置角度和速度。而且利用转子固有高频信号来检测转子位置解决了实际系统中转子高频信号的注入问题,大大加强了本方法的实用性。最后通过仿真分析验证了本文提出的无机械位置传感器检测方法的正确性和实用性。
[1] Sarma S,Agrawal V K,et cl.Instantaneous angular position and speed measurement using a DSP based resolver-to-digital converter[J].Measurement,2008(41):788 - 796.
[2] 李志民,张遇杰.同步电动机调速系统[M].北京:机械工业出版社,1996.
[3] Matthew J,Robert D Lorenz.Rotor Position and Velocity Estimation for a Salient-Pole Permanent Magnet Synchronous Machine at Standstill and High Speeds[J].IEEE Transactions on Industry Applications,1998,34(4):784 -789.
[4] 张俊科.同步机与旋转变压器信号幅值的测试[J].微电机,1993,26(1),30 -32.
[5] 万山明,吴芳,黄声华.基于高频电压信号注入的永磁同步电机转子初始位置估计[J].中国电机工程学报,2008,33(28):82-86.
[6] 邓先明,马志勋,李新宇,等.转子注入高频的同步电机无传感器控制[J].电机与控制学报,2010(10):61-67.

