基于负载电流谐波特征的并联型有源电力滤波器交流电感额定值计算公式
田铭兴,杨雪淞,阎 宏,张俊强
(兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070)
0 引言
随着国民经济的发展,大规模的整流设备等非线性负荷的广泛使用,其产生的谐波对电力系统的电能质量造成了极大的污染。而有源电力滤波器(APF)的研究及工程应用可以对电网进行谐波和无功功率的动态补偿及改善,以此来保证电力系统的正常运行[1-2]。
目前,对APF的研究主要集中在对其拓扑结构、谐波检测和控制方法上。文献[3-5] 都是对现有的几种APF的拓扑结构以及应用进行了综述和分析,并以此展望了APF的发展前景。在谐波检测和补偿电流的控制方法上,提出了如瞬时无功理论、坐标变换、模糊反馈电流检测、自适应谐波电流检测等一系列谐波电流检测方法[6-8];控制方法上采用了如电流滞环控制、空间矢量控制、PI控制等方法[9-13]。然而,APF主电路交流电感和直流电压等关键参数的选取同样对整个设备的补偿性能起着至关重要的作用[14]。
许多学者对APF交流电感和直流电压的选取做了大量的研究[15-21],取得了一定成果,但在以下3个方面还需进一步研究:能够满足特定负载类型所有工况下的补偿要求的交流电感和直流电压额定值的确定;负荷类型和谐波特征对交流电感和直流电压影响的有效考虑;交流电感和直流电压的计算公式应该易于解析计算和理论分析。本文根据满足电流跟踪能力的APF电压约束方程以及所选交流电感和直流电压应尽量小的原则,给出了APF交流电感和直流电压的额定值计算公式。最后,通过与文献[18] 的结果比较,说明本文分析更加合理。
1 交流电感和直流电压的取值范围
APF等效电路图如图1所示[19]。图中,us为电源电压;uf为APF交流侧电压;is为电源电流;ip为APF交流侧电流(或称补偿电流);il为负载电流;R和L为APF交流侧电阻和电感。
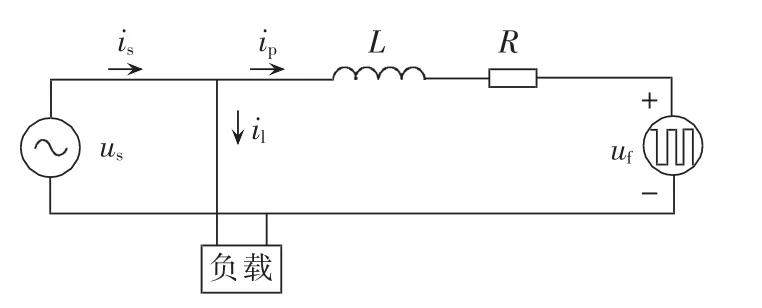
图1 APF系统等效电路图Fig.1 Equivalent circuit of APF
由图1可得:
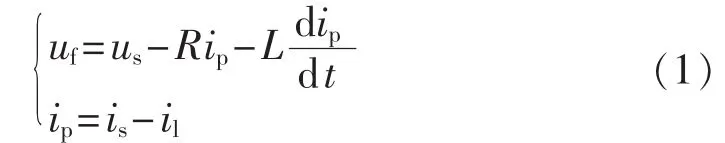
为了保证APF对补偿电流具有绝对的控制力(即要有足够的跟踪能力),则需满足:
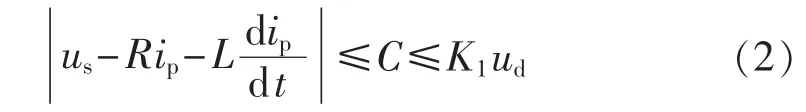
其中,C为某个大于零的实数;ud为直流侧电压。对于单相APF系统,K1=1;对于三相APF系统,K1=2/3。式(2)即为APF满足电流跟踪能力的电压约束方程。
严格来讲,由于 us、ip、ud是时间的任意函数,特别是ip、ud还因APF工作状况的不同而不同,所以若要直接通过式(2)求解L并不容易。即使求解出来L,还存在实际设计中如何选择L额定值的困难。所以,在通过式(2)求解满足保证APF对补偿电流具有绝对的控制力的L时总要做一些假设和简化处理。
一般假设电源电压为纯正弦、忽略电流高次谐波对ud的影响、所要补偿的谐波次数为N,则有:
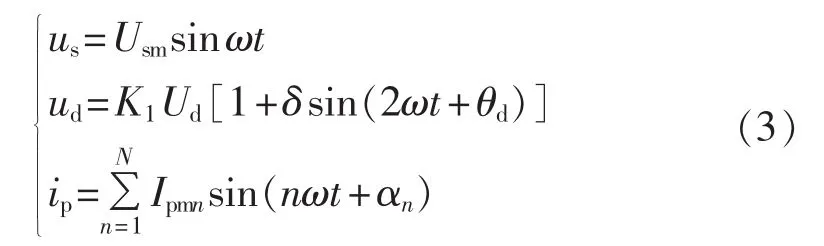
其中,Usm为电源电压幅值;θd为直流电压2次谐波相位角;Ipmn为补偿电流n次谐波幅值;αn为补偿电流n次谐波相位角;Ud为直流电压;δ为直流电压波动率,一般δ≪1。
把式(3)的第 2个公式代入式(2)得:
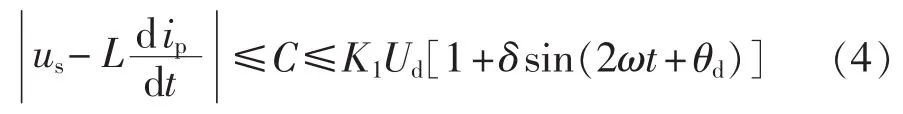
又由于:
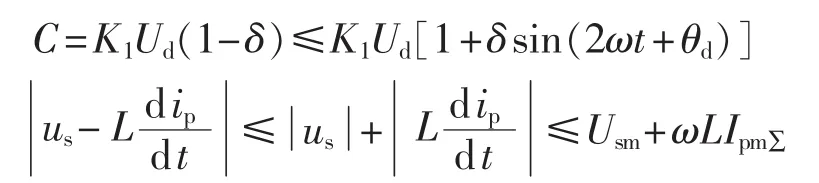
其中,Ipm∑为补偿电流各次谐波幅值之和,可由式(5)计算得到。
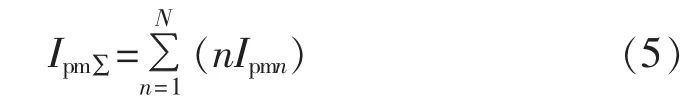
由式(5)并结合式(1)可知,Ipm∑直接取决于负载电流。
所以,若满足:
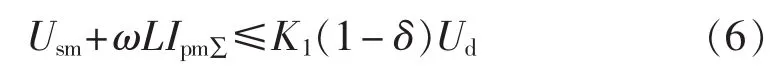
则式(4)成立。因此由式(6)可得:
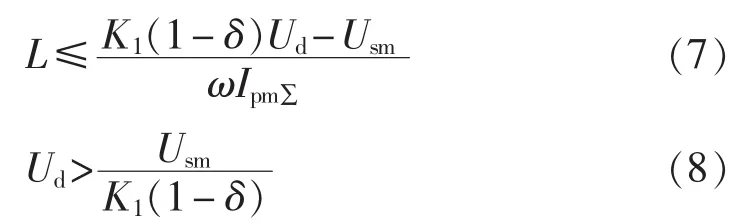
式(7)、(8)分别给出了保证 APF对补偿电流具有足够跟踪能力的交流电感L最大值和直流电压Ud最小值。由此可以看出,若要提高电流跟随性,电感L越小越好。但是,电感L越小,电流中高次谐波就越大。过大的高次谐波会污染电网,从而对高频滤波又提出了更高的要求。所以,电感L取值应有下限值。这里直接引用文献[19] 的公式:

其中,hmax为补偿电流脉动量最大值;fsmax为最高开关频率。对于三相双极性调制,K2=3π2;对于单相单极性调制,K2=2π2;对于单相双极性调制,K2=π2/2。
由式(7)、(9)可得交流电感的取值范围是:
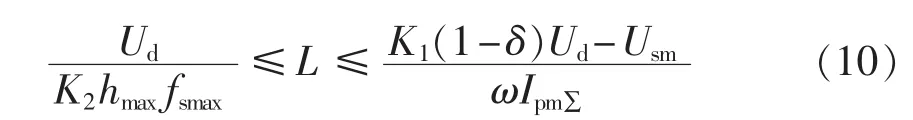
2 交流电感和直流电压的额定值
尽管式(8)、(10)给出了满足对补偿电流跟踪能力和高次谐波限制要求的交流电感和直流电压取值范围,但在实际设计中,总要选定一个电感值和电压值(称之为额定值)。所选择的交流电感和直流电压的额定值应该在补偿电流变化的全部范围内都能满足对补偿电流的跟随,且高次谐波不超过所允许的最大值。同时,为了减小成本,交流电感和直流电压取值应该尽量小。
由于:
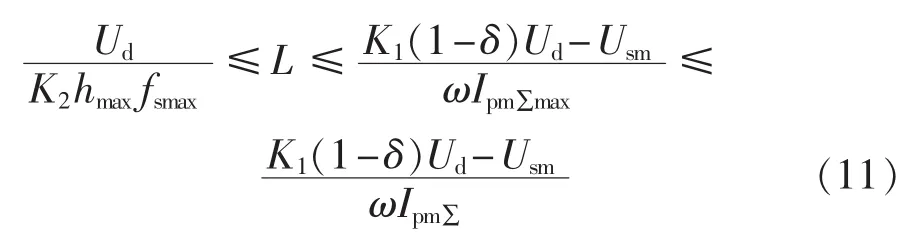
其中,Ipm∑max为补偿电流各次谐波幅值之和的最大值。
若要式(11)有解,则:
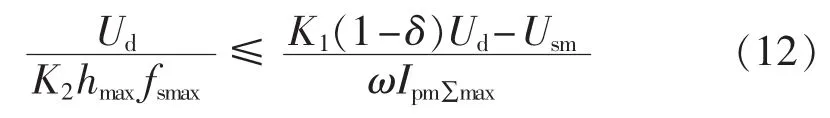
由式(12)可得:
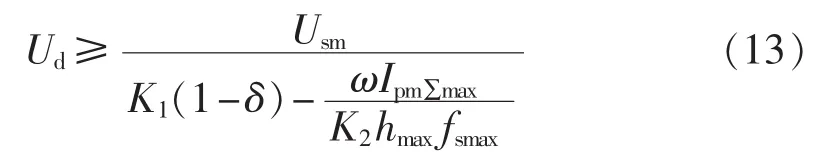
为了使直流电压尽量小,直流电压额定值应取式(13)的下限,即:
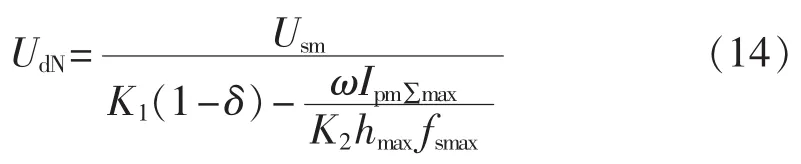
把式(14)代入式(11)可得交流电感的额定值为:
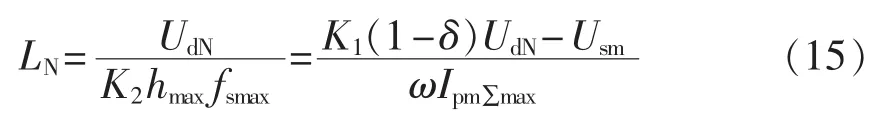
由式(14)、(15)可知,交流电感和直流电压额定值应在补偿电流各次谐波幅值之和、电流脉动量以及开关频率都为最大值条件下取得。这样做的好处是:最大的补偿电流各次谐波幅值之和、电流脉动量以及开关频率是明确易知的;交流电感和直流电压额定值都为其取值范围内的最小值;在APF实际运行中,补偿电流各次谐波幅值之和应小于等于其最大值。当补偿电流各次谐波幅值之和小于其最大值时,由式(11)、(14)、(15)可知,此时交流电感 L 的理论计算值的最小值等于其额定值,理论计算值的最大值大于其额定值,这说明交流电感额定值LN满足要求,且在电流脉动量不超过最大脉动量的同时具有更快的跟踪速度。因此,如果根据式(14)、(15)计算所得交流电感和直流电压作为其额定值,在补偿电流变化的全部范围内都能满足对补偿电流跟随性和脉动量(高次谐波)的补偿要求,且取值较小。
3 补偿电流各次谐波幅值之和
由式(14)、(15)可知,若要计算交流电感和直流电压的额定值,则必须先要知道补偿电流各次谐波幅值之和的最大值,即APF交流电感和直流电压的额定值的选择要针对所要补偿的非线性负载。尽管非线性负载多种多样,但整流电路所占比例最大。不失一般性,本文以三相桥式相控整流桥为例来说明。
如果三相APF所补偿的负载是三相桥式相控整流电路,其负载为强感性负载,忽略其换相过程和直流电流脉动,且补偿后电源电流为负载电流基波有功分量,则取a相时对应图1中负载电流为:
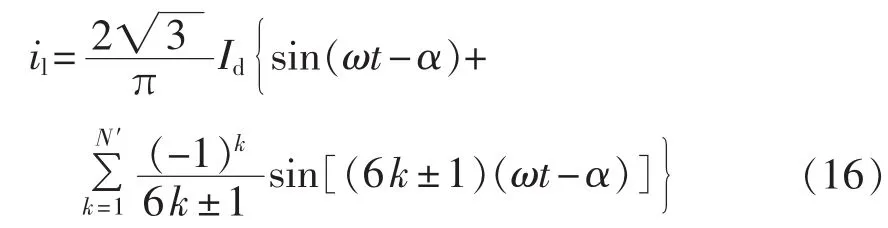
其中,Id为整流电路直流侧平均电流;α为以a相电源电压过零点为计时起点时的触发角,移相范围为0°~90°;N′和所需滤除的最高谐波次数 N的关系是N=6N′+1。
令补偿后电源电流为纯有功电流,即:
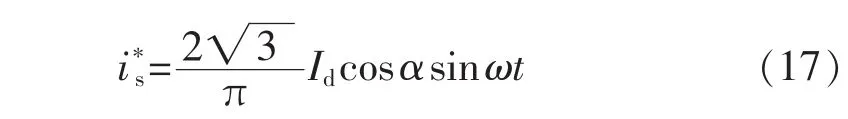
则由式(1)、(16)可得:
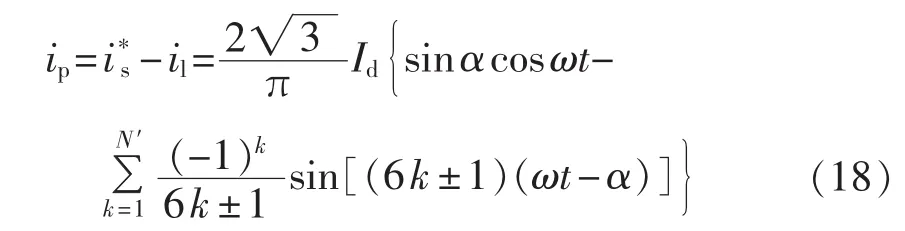
把式(18)代入式(5)可得补偿电流各次谐波幅值之和为:
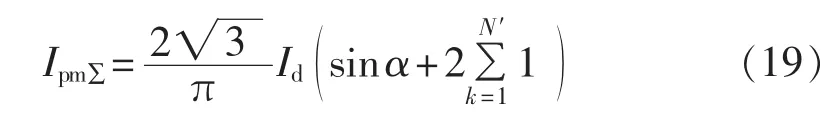
考虑到:
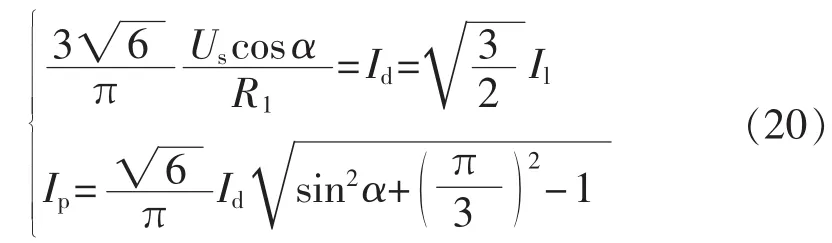
其中,Us为电源相电压有效值;R1为整流电路直流侧负载电阻;Il为三相桥式相控整流桥交流侧相电流有效值;Ip为APF交流侧相电流有效值。
由式(19)可知,补偿电流各次谐波幅值之和随着触发角的不同而不同。由于当N′比较大时有:
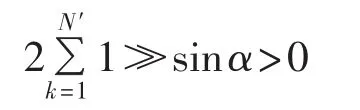
则式(19)、(20)可分别近似为:
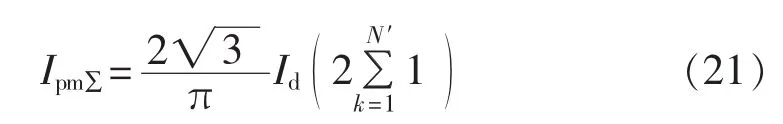
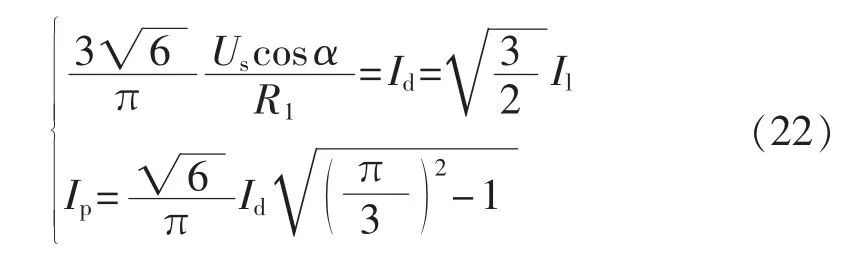
由式(22)可知,当 α=0°时,Id取得最大值,也为整流桥直流侧平均电流的额定值IdN。相应地,Il、Ip取得最大值,也分别为其额定值 IlN、IpN,同时,Ipm∑的最大值为:
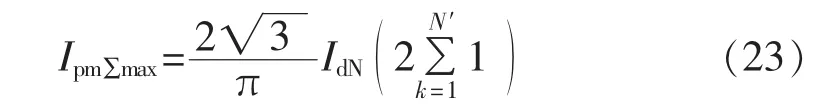
且:
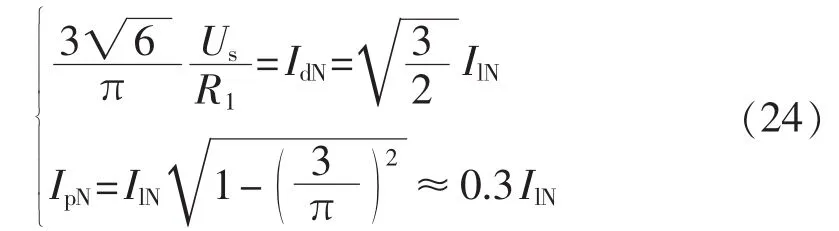
其中,IlN为三相桥式相控整流桥交流侧电流额定值(APF所补偿的负载电流额定值);IpN为APF交流侧电流额定值。
所以,当已知电源相电压额定值和整流桥直流侧电阻、或整流桥直流侧平均电流额定值、或整流桥交流侧相电流额定值、或APF交流侧相电流额定值时,可由式(23)计算出补偿电流各次谐波幅值之和的最大值,从而由式(14)、(15)即可算得负载为三相相控整流负载时APF的交流电感额定值和直流电压额定值。
尽管式(23)是针对三相桥式相控整流桥推导出的,但可以预料,其他类型(至少有一部分)非线性负载的补偿电流各次谐波幅值之和的最大值也存在如式(23)所示的定量解析关系。如果是这样,对于特定类型非线性负载,只要给定负载的额定电流,就可以根据式(14)、(15)选定其交流电感和直流电压的额定值,从而避开了交流电感和直流侧平均电压的选择需要考虑负载谐波电流具体成分的困难。
4 算例
已知(便于比较,引用文献[18] )的算例参数:电源额定相电压UsN=220 V,三相桥式相控整流桥交流侧电流额定值IlN=100 A,APF最高开关频率fsmax=10 kHz,所要滤除最高谐波次数 N=25(对应N′=4),APF直流侧电压波动率δ=0,APF直流侧额定电压UdN=1 000 V。
由式(23)、(24)可得:
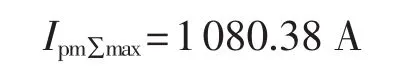
由式(14)可得:
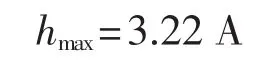
由式(15)可得:
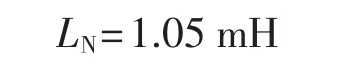
5 讨论
文献[18] 给出的交流电感上限值计算公式为(文献[18] 没有给出交流电感下限值的计算公式):
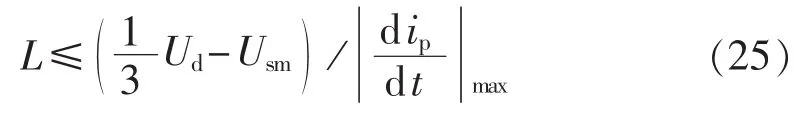
事实上,式(25)可由式(4)推得。
由于:
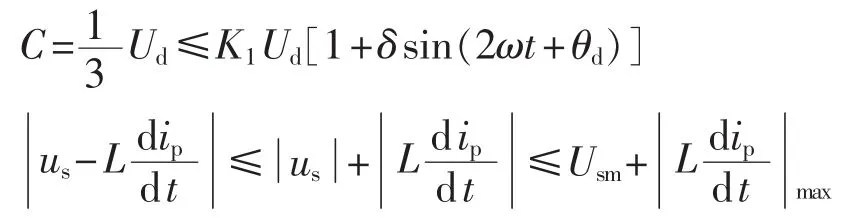
所以若:
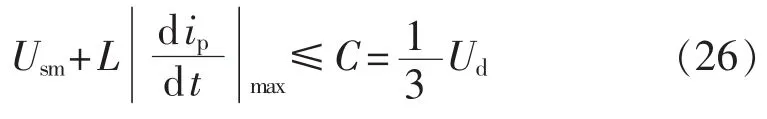
则式(4)成立。因此由式(26)可得式(25)。这意味着式(25)可由式(7)的推导思路导出,只是式(4)中C的取值不同。这也从一个方面说明式(2)或(4)具有一定的通用性。由于:
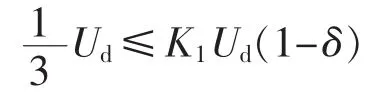
所以,式(25)算得的电感更小。这对保证电流跟踪性是有利的,但可能不满足对电流脉动的限制要求。
文献[18] 根据文献[21] 还给出了交流电感上限值的另一个计算公式为:
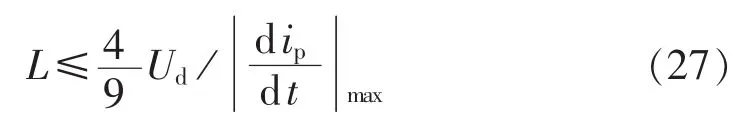
将文献[18] 给出的参数分别代入式(25)、(27)可得:L≤0.076 mH、L≤1.5 mH。文献[18] 分别在 L=0.076 mH、L=1 mH和L=1.5 mH条件下进行仿真分析。由文献[18] 的仿真和分析可看出:L=0.076mH的电流跟踪性最好,但其电流脉动很大;从所要补偿次数内的谐波补偿效果、电流跟踪能力以及高次谐波含量等方面综合来看,L=1 mH较L=1.5 mH更好。而根据本文式(15)算得LN=1.05 mH,所以所得的式(15)较式(25)、(27)更合理,而且直接给定交流电感的额定值(而不是一个范围)。另外,式(25)、(27)分母不易计算,其本身及其推导思路难以用于一般化的理论分析。
另外,由式(21)、(23)可得:

如果保持 Ud=UdN、h=hmax、δ不变,则由式(10)可得:
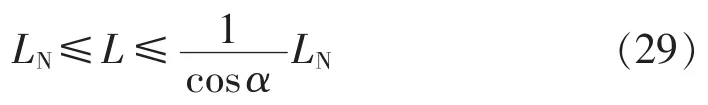
式(29)说明,当 α≠0°时,如果保持 Ud=UdN、h=hmax、δ不变,则所选定的LN满足要求,而且是此种情况下交流电感取值范围的下限,这意味着在电流脉动量不超过最大脉动量的同时具有更快的跟踪速度,同时,较小的交流电感也意味着设备具有更低的成本。
6 结论
本文提出了APF交流电感和直流电压额定值的计算公式。该公式具有以下特点:所计算出的交流电感和直流电压额定值能够满足特定负载类型所有工况下的补偿要求;易于考虑所补偿的电流谐波特征,且便于计算和理论分析。

