基于扩展卡尔曼滤波的永磁同步电动机低速研究

丁宇汉，焦振宏，孙百军，郑 勇

(西北工业大学，陕西西安710072)

0 引 言

永磁同步电动机由于本身的许多优点比如结构简单、转矩/惯性大、功率密度大、效率高、维护容易等，被广泛应用于数控机床、航空航天、机器人等高精度控制系统［1］。在永磁同步电动机控制系统中，矢量控制的使用，使得能够模拟直流电动机一样对永磁同步电机进行控制，从而获得较高的调速性能［2］。高性能控制系统一般都需要高精度的位置传感器，这些传感器的价格较贵。通常使用光电编码器在一个旋转周期发出固定的脉冲数，通过计算光电编码器在测量时间发出的脉冲数目得到转子位置，转子位置微分就是转子速度。由于编码器是量化脉冲，当电动机运行在低速状态时，每个采样时间内获得的脉冲数极少，从而使得转子的位置和速度计算精度变差，有时会产生大的误差和微分噪声［3］。在控制系统中，负载转矩的变化会使得转速产生振荡，为了使得速度在负载转矩变化时仍然稳定，就需要负载转矩信息用以补偿参考转矩、减小负载转矩变化对速度稳态的影响［4］。

为了有效解决上述问题，就需要一种可以同时观测转子位置、速度和负载的状态观测器。因此，本文提出了一种新型的基于扩展卡尔曼滤波器的观测器。卡尔曼滤波器可以直接解决非线性方程，并且考虑参数误差的影响，以及测量扰动等，因此有很强鲁棒性，并且能消除测量噪声和误差［5－6］。考虑到观测器设计需要表达转动惯量，对转动惯量进行了在线辨识，目前常用的辨识方法有最小二乘法、卡尔曼滤波法、模型参考自适应法(MRAS)、遗传算法以及神经网络模糊控制法［7－8］。本文使用易于实现的最小二乘法对转动惯量进行辨识，以提高观测器性能。

1 基于扩展卡尔曼滤波的观测器

永磁同步电动机的机械运动方程:

式中:ωr、θr、J、F、Te、TL分别表示转子机械角速度、机械位置、转动惯量、摩擦系数、电磁转矩和负载转矩。相对于转子的速度和位置的变化来说，负载转矩的变化非常慢，可以近似认为没有变化，即有:

选取转子速度、位置和负载转矩作为状态变量，转子位置作为输出，建立基于扩展卡尔曼滤波的观测器。

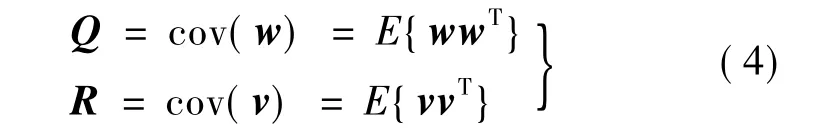
Q阵和R阵均为非负定阵，实际应用中根据经验进行调整。

在采样时间Ts足够小的情况下，转移矩阵:

通过重复下面计算步骤，可以获得离散非线性卡尔曼滤波器方程:

(1)一步预估

(2)一步预测均方差

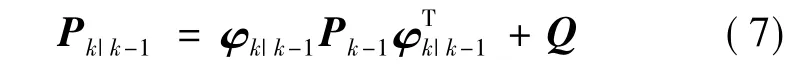
(3)滤波增益阵

(4)状态估计

(5)估计均方误差阵

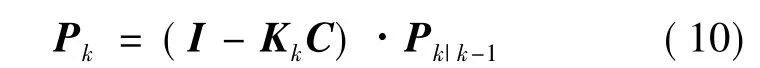
式中:α是很大的正数，I是单位矩阵。在式(11)的条件下并不能保证系统是无偏差的。事实上，如果系统是一致完全随机可控和可观，则卡尔曼滤波一定是渐近稳定的，随着滤波步数的增加，盲目选取的初始状态x0和P0对滤波和Pk值的影响将逐渐减弱直至消失，估计逐渐趋向无偏差［9］。

2 转动惯量的参数辨识

2.1 最小二乘法原理及实现

最小二乘法是工程中常用的辨识方法，是一种比较成熟的方法［10］，图1为最小二乘法的表达形式。图中h(k)、y(k)、z(k)、e(k)、θ 分别表示输入量、输出量、均值为零的随机噪声以及未知模型参数，记:

图1 最小二乘法的表达形式

模型的输出可表示:

则使得Y(θ)最小θ的估计值 称为参数θ的最小二乘估算值。由此，可以推导出递推最小二乘法的表达式:

若记:

得到递推公式:

式中:α是很大的正实数(104～106);ε为零向量。

2.2 转动惯量辨识的实现

在忽略系统摩擦阻力的情况下永磁同步电动机的运动方程:

定理4 内幂零群G=PQ,其中P为正规Sylow p-子群,Q为循环Sylow q-子群(见引理7),则其幂图P(G)可平面化当且仅当G为以下情形之一:

将上式进行离散化处理:

由于采样频率很高，负载转矩变化很慢可以忽略，将式(24)减去式(25)得:

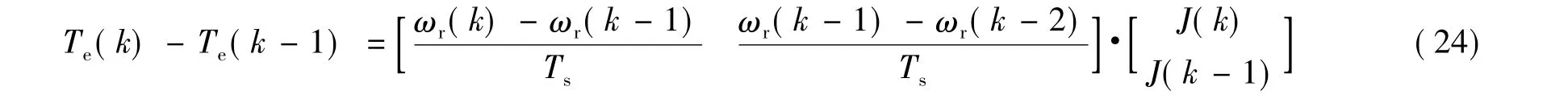
令:

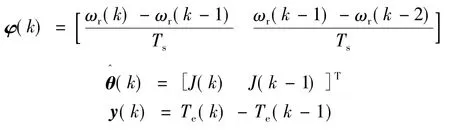
得到转动惯量参数辨识的最小二乘法形式:

3 控制系统的总体实现

本文采用的永磁同步电动机控制策略为目前应用较广的空间矢量调制的转子磁场定向id=0控制策略。主要包括永磁同步电动机、空间电压矢量调制(SVPWM)模块、逆变器模块、编码器、转动惯量辨识模块和扩展卡尔曼滤波观测器模块。系统框图如图2所示。

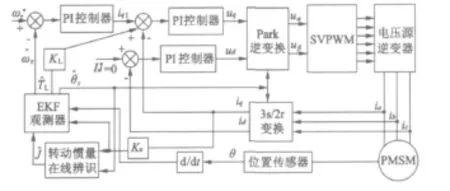
图2 系统控制框图

4 仿真分析

为了验证所设计的观测器的性能，在Matlab/Simulink下建立起如图3所示的各个功能模块，并将它们结合起来，得到整体的仿真模型。

图3 系统整体仿真图

仿真所用的永磁同步电动机参数如表1所示。

表1 永磁同步电动机参数

仿真用编码器精度为2 500线，卡尔曼滤波器的Q阵和 R阵经过仿真，最后设置:Q=diag(［1 0.1 10］)，R=diag(［1000］)。

初始值的设定:x^= ［0 0 1］T，P0=diag(［1 000 000 1 000 000 1 000 000］)。

速度给定为3 r/min，负载转矩开始给定为1 N·m，在0.15 s时突变为1.5 N·m。未引入转矩反馈和引入转矩反馈的曲线如图4～图6所示。

负载转矩给定恒定为1 N·m，速度给定开始时为3 r/min，转动惯量开始为 0.000 7 kg·m2，在0.13 s时突变为 0.001 kg·m2，在 0.16 s时速度给定变化为5 r/min，未引入转动惯量辨识和引入转动惯量辨识的曲线如图7～图9所示。

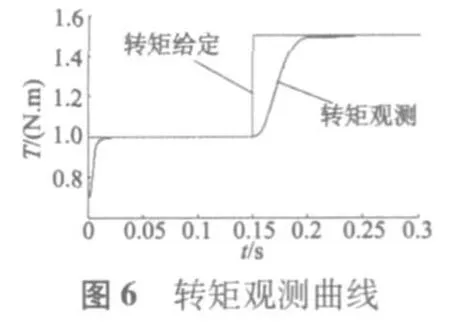
由图4～图6可见，如果没有引入负载反馈补偿，当负载发生突变时，速度降落比较明显;而引入负载转矩反馈补偿后，负载突变引起的电流落差由反馈进行了补偿，减小了转速降落，改善了转速。

由图7～图9可知，当系统运行在稳定状态时，转动惯量的变化对系统的性能几乎没有影响，说明了在稳态时卡尔曼滤波器对于系统参数的鲁棒性;但是，当速度给定发生改变后，如果没有反馈辨识的转动惯量，系统恢复稳态的过程中速度的响应会比较慢，并且有较大的超调，而引入转动惯量反馈后，响应较快，超调明显减小，改善了系统性能。

5 结 语

针对永磁同步电动机低速控制系统，在使用的编码器精度较低时，获得的转子转速和位置都不是很准确，本文提出了一种基于扩展卡尔曼滤波器的观测器。该观测器对参数依赖小。为了减小负载转矩突变引起的转速降，以及观测器对转矩变化不敏感，同时设计了观测器对负载转矩进行观测并用于补偿，有效减小了负载突变引起的转速降。同时，为提高系统的鲁棒性，对观测器设计中需要用到的转动惯量进行在线辨识。仿真结果表明，本文设计基于的新型观测器的控制策略，应用于矢量调制的永磁同步电动机低速控制系统中是有效可行的，改善了系统的控制性能。

［1］ Nakai H，Ohtani H，Satoh E，et al.Development and testing of the torque control for the permanent－ magnet synchronous motor［J］.IEEE Trans.Ind.Electron，2005，52(4):800 －806.

［2］ 许峻峰，冯江华，许建平.永磁同步电动机控制策略综述［J］.机车电传动，2005(5):7－11.

［3］ Zheng Zedong，Fadel M，Li Yongdong.A High － Performance Control System of PMSM Based on Torque Observor［C］//Power Electronics Specialists Conference(PESC).2007:587 －592.

［4］ Shi Tingna，Wei Linrui，Dan Xiao.Sliding mode control of PMSM based on load observer［C］//International Conference on Electrical and Control Engineering(ICECE).2010:4216 －4219.

［5］ Gu Shanmao，He Fengyou，Zhang Hui.Study on Extend Kalman Filter at Low Speed in Sensorless PMSM Drive［C］//International Conference on Electrical Computer Technology(ICECE).2009:311 －316.

［6］ Benchabane F，Titaouine A，Bennis O，et al.Systematic fuzzy sliding mode approach combined with extended Kalman filter for permanent magnet synchronous motor control［C］//International Conference on Syetems Man and Cybernetics(ICSMCE).2010:2169－2174.

［7］ Senjyu T，Kinjo K，Urasaki N，et al.Parameter measurement for PMSM using adaptive identification［J］.IEEE Trans.Ind.Electron，2002，3:711 －716.

［8］ 庞中华，崔红.系统辨识与自适应控制MATLAB仿真［M］.北京航空航天大学出版社，2009:25－35.

［9］ 吴永前.永磁同步电机无位置传感器调速系统的研究［D］.西安:西北工业大学，2001.

［10］ 王鸿山，张兴，杨椒英，等.基于最小二乘法在线参数辨识的异步电动机矢量控制仿真［J］.合肥工业大学学报，2009，32(4):496－499.