三轴稳定航天器多领域统一建模与仿真平台

徐文福，梁 斌，李 成

(1.哈尔滨工业大学深圳研究生院，518055深圳，wfxu@hit.edu.cn;2.深圳航天东方红海特卫星有限公司，518057深圳)

三轴稳定航天器多领域统一建模与仿真平台

徐文福1，2，梁 斌1，李 成1

(1.哈尔滨工业大学深圳研究生院，518055深圳，wfxu@hit.edu.cn;2.深圳航天东方红海特卫星有限公司，518057深圳)

为反映航天器系统涉及的多学科交互作用下的控制特性，开发了包含机械、电气、控制、软件等的多领域统一建模与仿真平台.该平台包含姿控软件、飞轮系统(电机及其驱动器、轴承摩擦、飞轮机构等)、磁力矩器、姿态敏感器、姿态动力学、轨道动力学、环境力矩等不同领域的模块，各模块由Modelica语言实现，有机集成一体.对两种典型的姿态控制模式——姿态建立及姿态机动的仿真表明，利用该仿真平台不但可分析整个系统的闭环控制性能，还可评估各领域部件对整体性能的影响.在航天器研制的各个阶段(方案、子系统、系统等)充分使用该平台，可实现多学科设计优化的目标.

航天器;多领域建模;仿真;三轴稳定;姿态控制

航天器系统涉及的学科领域很多，包括机械、电气、轨道动力学、姿态动力学、自动控制、计算机(含软件和硬件)等等.以往的研究中，各领域部件间的交互作用往往被粗略的近似.设计性能良好的控制器，必须将机械、电气及控制系统纳入统一框架内［1］，开展多领域建模与仿真研究，以实现多学科优化设计(Multidisciplinary Design Optimization，MDO)的目标［2］.

多领域建模与仿真方法主要有3种:基于接口的方法，基于高层体系结构(High Level Architecture，HLA)的方法［3］，以及基于统一建模语言的方法［4］.基于统一建模语言的方法对来自不同领域的系统构件采用统一方式进行描述，彻底实现了不同领域模型之间的无缝集成和数据交换［5］.本文借鉴最新的多领域统一建模思想，开发了基于Modelica语言(开发环境为Dymola)的三轴稳定航天器系统的多领域统一建模与仿真平台，将姿态控制系统(AOCS)、飞轮系统、磁力矩器、轨道动力学模型、姿态动力学、环境模型(地磁场、重力梯度等)、敏感器模型等集成一体，可实现飞轮零动量、偏置动量等模式下的三轴姿态机动的建模与仿真，以验证关键的算法.该建模与仿真系统包含了机械、电气、磁场、控制等多个领域的模型，在统一的环境下即可进行闭环的仿真，效率、准确性大大提高.

1 航天器控制系统仿真的模块划分

为实现航天器系统在轨任务的控制仿真，所建立的模型需包含如下功能模块:

1)航天器姿态及轨道控制系统(AOCS).由星载处理器(硬件)及运行在其上的软件组成，其中软件用于实现工作模式管理、姿态确定、姿态控制、卸载逻辑等算法.其输入为所采集的各敏感器数据，输出为执行机构的控制指令.对于推力器，控制指令为开/关时间;对于飞轮，控制指令为电机的驱动电流;对于磁力矩器，控制指令为控制电压.一些先进的智能控制方法如文献［6－8］可在此模块中实现.

2)执行机构.根据AOCS输出的控制指令执行相应的动作，以产生对航天器的作用力/力矩.常用的执行机构包括推力器(因为需要消耗宝贵的燃料，长寿命卫星的姿态控制慎用)、飞轮组以及磁力矩器.

3)航天器姿态动力学.反映航天器系统的姿态运动规律，输入为控制力矩，输出为航天器姿态角(采用欧拉角或四元数表示)及姿态角速度.

4)敏感器模型.提供姿态控制所需要的测量信息，包括速率陀螺、地球敏感器、太阳敏感器、星敏感器等.对于需要执行对目标飞行器的跟踪接近、交会对接等任务的航天器，一般还装有加速度计.

5)轨道环境模型.建立航天器所处轨道的环境条件，包括地球磁场、地球引力场、太阳光照、大气模型等，据此可计算环境干扰力和力矩;对于多个航天器的跟踪、接近等的建模和仿真，可采用文献［9］的方法建立相对轨道动力学模型.

(6)环境干扰力和力矩模型.根据轨道环境条件，计算航天器在轨所受的各种干扰力、力矩，包括剩磁力矩、重力梯度力矩、太阳光压、气动力/力矩等.

(7)轨道动力学及时间系统.计算给定时刻航天器质心的惯性位置和速度，并可换算出轨道坐标系相对于地心惯性系的位置和姿态.该模块的输出作为环境模型的输入.

2 多领域统一建模与仿真平台

2.1 总体框图

不失一般性，假设所研究的航天器系统为对地观测卫星，执行任务时需要保持对地的三轴稳定姿态.该航天器以4个飞轮(3正交+1斜装)和三轴磁力矩器作为执行机构，以三轴速率陀螺、红外地球敏感器、太阳敏感器及星敏感器作为姿态测量部件.

所建立的航天器系统的多领域统一建模与仿真平台如图1所示，包括飞行任务管理模块(Mission)、航天器姿轨控系统(AOCS，实现模式管理、姿态确定、姿态控制等算法)、飞轮组(Flywheels，含电机及其驱动器、轴承、摩擦力矩、旋转体等)、磁力矩器(Magnetorquer，用于飞轮卸载)、轨道动力学及环境干扰(OrbitDynAndDis，实现轨道动力学、轨道环境、干扰力/力矩计算等)、姿态动力学模块(SatThreeAxis)等.任务管理模块用于根据具体的飞行任务产生期望的姿态角AAttD、角速度Wd;AOCS模块还接受姿态敏感器模块Sensors测量值——本体姿态四元数 Qbo、姿态角速度Wbo(本体系相对于轨道系)和Wbi(本体系相对于惯性系)，飞轮模块输出的角速度Wf以及轨道动力学模块OrbitDynAndDis输出的磁场强度Bb(用于飞轮卸载)，采用相应的姿态、轨道控制算法，产生执行机构控制指令——4个飞轮的控制电流ux、uy、uz、us，以及磁力矩器的控制电压 um;飞轮模块Flywheels、磁力矩器根据控制指令，产生相应的作用力矩，作用于卫星本体SatThreeAxis;姿态动力学模块SatThreeAxis根据执行机构的控制力矩，及OrbitDynAndDis模块输出的环境干扰力矩，计算本体姿态的变化情况，输出当前姿态角Qbi、角速度Wbi;轨道动力学及环境干扰模块OrbitDynAndDis根据卫星所处的姿态Qbi、角速度、轨道位置(模块内部迭代计算)，计算卫星本体系相对于轨道坐标系的姿态角、角速度、磁场强度、环境干扰力矩Td等;敏感器模块Sensors根据Sat－ThreeAxis和模块OrbitDynAndDis输出的姿态四元数、姿态角速度理论值，叠加测量噪声后，输出姿态测量值.

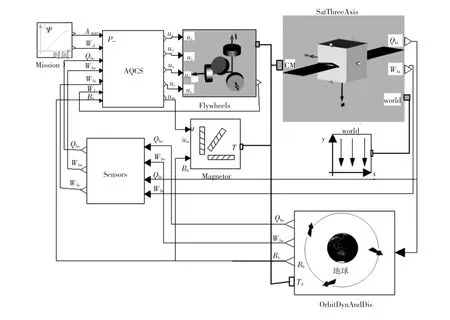
图1 航天器系统的多领域统一建模与仿真平台

2.2 姿态动力学的建模

在Dymola环境中，利用其自身的MultiBody库可以方便地建立航天器的姿态动力学模型.具体步骤如下:

1)建立世界坐标系.世界坐标系是姿态动力学方程的参考系，也是三维显示时的全局参考系(观测点).对于姿态动力学的建模，以轨道惯性系(原点为航天器质心，指向与惯性系一致，其中，惯性系为J2000坐标系)为参考系.

将MultiBody库中的 World图标(路径为MultiBody.World)拖到当前模型编辑窗中，双击该图标可对相关参数进行设置，将重力加速度g赋值为 0，即g=0.

2)建立航天器本体及其运动副.简单起见，假设航天器本体为一刚体(柔性体或带挠性附件的情况将后续给出)，通过定义其质量、惯量、质心位置、运动副，可完整反映其运动状态.首先创建1个 BodyShape(路径 MultiBody.Parts.Body－Shape)，更名为B0，并根据实际的数据给B0的相关参数赋值.双击该图标，弹出的对话框中，“General”界面定义质量特性，“Animation”界面定义几何外形.航天器的姿态运动具有3个转动自由度，因此通过定义球运动副可描述姿态的运动情况.

3)航天器理论姿态、角速度的输出.航天器理论姿态、角速度是各种姿态敏感器模型的输入.RelativeSensor(MultiBody.Sensors.RelativeSensor)可直接给出两坐标系之间的相对位置、线速度、线加速度;相对姿态、角速度以及角加速度.由于姿态动力学仅描述航天器姿态的变化过程，因此仅需输出姿态及角速度，其余不需要输出的状态通过设置其标志为“false”而禁止其输出.最后，将航天器的质心坐标系(CM)引出，以便与执行机构、环境干扰的参考坐标系连接;同时将理论姿态四元数、角速度，以及世界坐标系(World)引出.

2.3 执行机构的建模

2.3.1 飞轮组的建模

飞轮实质上是1个带有大转动惯量的力矩马达，由驱动电路、电机及轮体组成.其多领域模型如图2所示.飞轮有2种工作模式:力矩(电流)模式，动量(电压或转速)模式.本文所研究的航天器系统的飞轮采用力矩模式，其模型由驱动电流(输入端)、电机及其驱动电路(Motor1～Motor4)、轴承摩擦(bearingFriction1～ bearingFriction4)、转动关节 (Jx，Jy，Jz，Js)、轮体(Bx，By，Bz，Bs)，以及坐标转换关系(T1～T4)．其中，T1～T4分别建立了各飞轮安装坐标系相对于航天器系统质心坐标系的位置和姿态(frame－a1与系统质心坐标系CM直接连接，见图1)，而旋转关节定义了各轮体与航天器之间的旋转关系，电机及其轴承的输出轴与关节的驱动轴相连，同时，模型中将各个飞轮转动速度组成数组，通过输出端Spd输出.

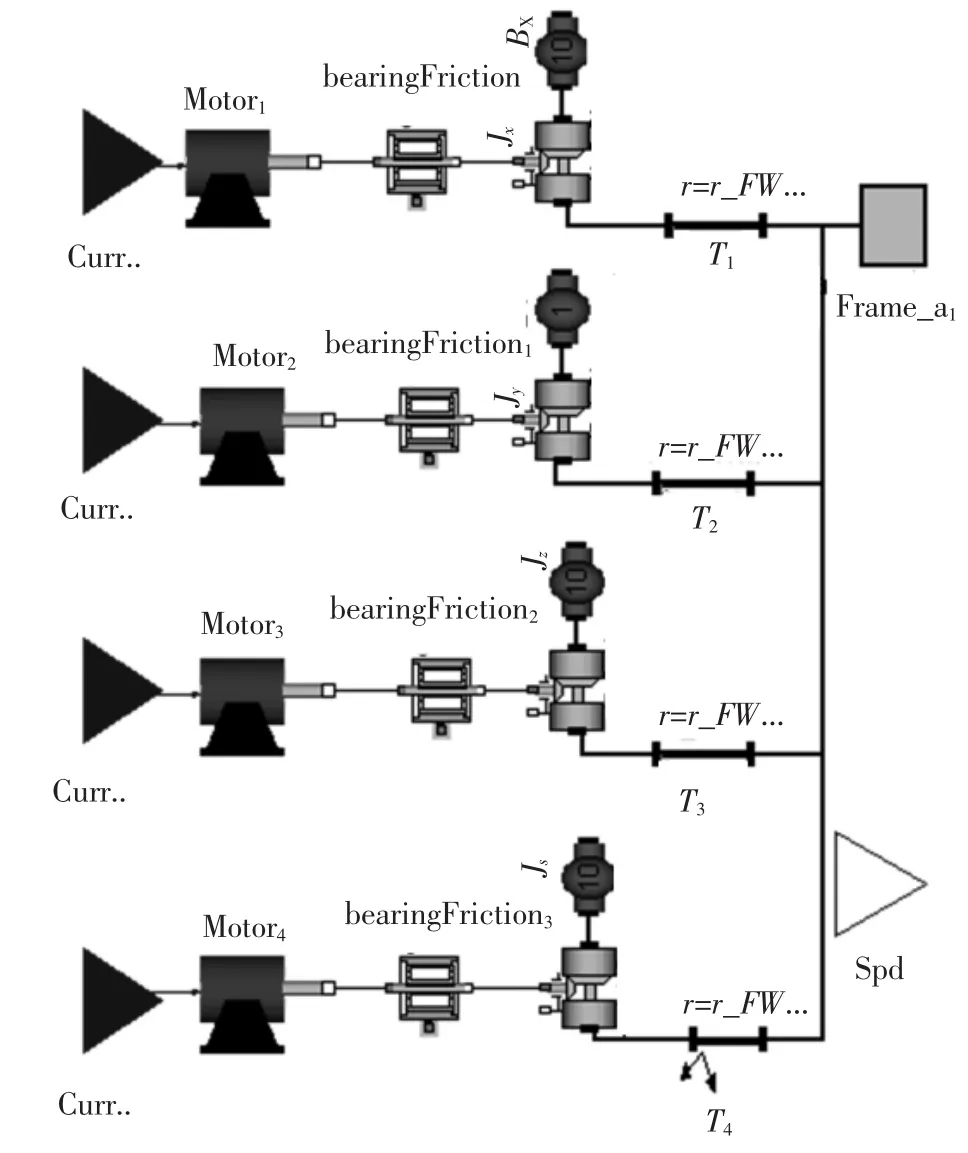
图2 飞轮系统的多领域模型

1)电机及其驱动器的建模.电机模型中包含了电枢电阻Ra、电枢电感La、反电动势emf、电机轴Jmotor等环节，驱动器部分由电阻(R)、电容(C)、运算放大器(Op)、电压源(Vs)及接地(g)等组成，除 Jmotor外(路径为 Modelica.Mechanics.Rotational.Inertia)，其它部分可在Modelica.Electrical.Analog.Basic中选取.所选用飞轮的电机及其驱动器相关参数及模型如图3所示.

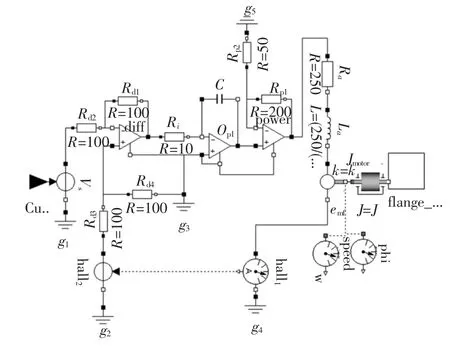
图3 电机(Motor1～Motor4)及其驱动器模型

2)轴承摩擦的建模.飞轮阻力矩包括轴承摩擦、风阻和电机损耗力矩3部分.飞轮壳体密封抽空，风阻很小;采用定子无铁心电机后，电机内部的电磁损耗力矩已不存在，因此，轴承摩擦是最主要的阻力矩.实验结果表明，阻力矩与飞轮转速之间有良好的线性关系，如下所示:

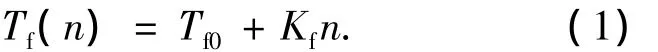
其中，n为飞轮转速;Tf0为电机启动时(0+速)需要克服的阻力矩(本质为滑动摩擦，比静止摩擦略小);Kf为摩擦系数．

在Dymola环境中，利用元件BearingFriction(路径为 Modelica.Mechanics.Rotational.Bearing－Friction)可以很方便的建立如式(1)的轴承摩擦模型.将相关参数转为BearingFriction定义的格式(同时注意转速的单位需统一为 rad/s)，如下所示:

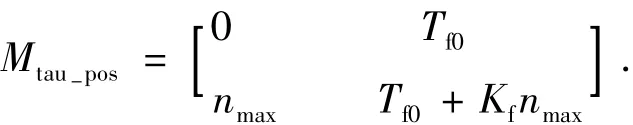
另外，通过定义参数Mpeak(默认值为1)，可区分静止摩擦Tfs与Tf0，即静止摩擦Tfs=Mpeak·Tf0．

2.3.2 磁力矩器的建模

磁力矩器利用自身的磁性线圈产生磁偶极子矩，与地球磁场相互作用而产生作用于卫星的控制力矩，可用于补偿小干扰力矩引起的姿态偏移和对动量交换装置进行卸载.本文所建三轴磁力矩器的模型，输入为三轴磁力矩器的控制电压，该控制电压与磁矩电压系数KBu(与KuB互为倒数)相乘并经过限幅(限制在最大、最小磁矩之间)后得到磁力矩器的磁矩，与地磁场强度在本体坐标系下的矢量为Bb进行叉乘即得到作用于本体的力矩．

2.4 轨道动力学及环境的建模

2.4.1 轨道动力学

采用二体开普勒万有引力模型作为轨道动力学模型.星体轨道参数在J2000.0的直角坐标系下描述，忽略地球岁差、章动和极移的影响.中心天体和飞行器均作为质点对待，分别记作M和m，讨论飞行器m相对天体M的运动，相应的运动方程为

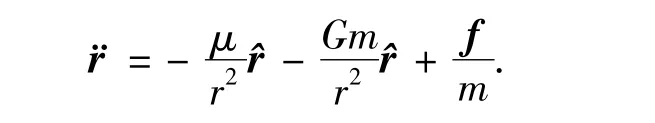
2.4.2 地球磁场与地磁力矩

地磁场按其起源可分为内源场和外源场.在1 000 km以下的高度范围内，平静时的外源场的强度不到内源场的千分之一，强扰动时的外源场也在内源场的百分之一以下.略去外部磁场的影响，在地理坐标系下卫星三轴的地磁场强度为［10］

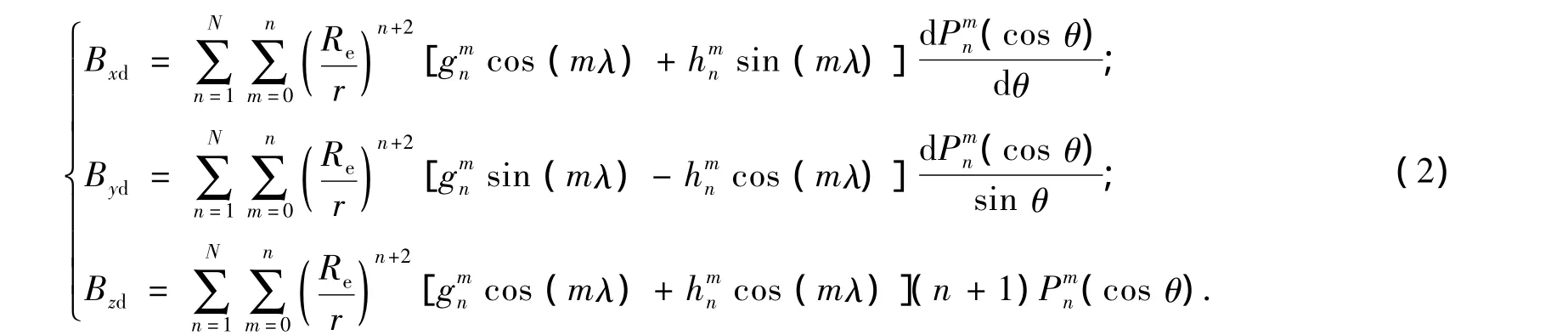
式中:Re=6 378.137 km(地球赤道平均半径)为地球半径;r为航天器的地心矩;θ为地心余纬;λ为格林尼治算起的东经;gmn、hmn为基本磁场的高斯系数;Pmn(cos θ)为n次m阶的关联勒让德函数．本文中采用IGRF2000(国际基准地磁场)的6×6阶系数.

由式(2)计算得到的地磁场强度为在地理坐标系中的分量，利用地理坐标系与轨道坐标系的转换公式，可求得卫星所在处的地磁矢量B在轨道坐标系的分量(Bxo，Byo，Bzo)，然后借助姿态方向余弦矩阵给出B在卫星本体坐标系中的分量(Bxb，BybBzb)，记为 Bb= ［BxbBybBzb］T．假定卫星体内的等效磁矩Mb=［MxbMybMzb］T，则作用于星体上的磁力矩为Tm=Mb×Bb．

2.4.3 重力梯度力矩

重力梯度力矩对航天器的姿态运动的影响十分重要．在与距离平方成反比的引力场内作轨道运动的任何物体，只要其质量分布是非对称的，都将受重力梯度力矩的作用．力矩的大小按下式计算:

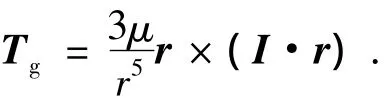
2.4.4 大气环境模型

按下述公式计算气动力和气动力矩:

式中:ρV2R/2为动压头;CD为阻尼系数，取值范围为2.2～2.6;Ap为迎流面面积;Cp为卫星质心至压心的矢径;v为来流方向的单位矢量．

2.4.5 太阳辐射力矩

辐射力矩主要由太阳光压造成，地球反照及大气红外辐射是次要的辐射源．太阳辐射力矩基本上与高度无关，近似为常数．

辐射力矩的物理机制是辐射粒子与卫星表面的动量交换．在工程实用中，辐射力矩为

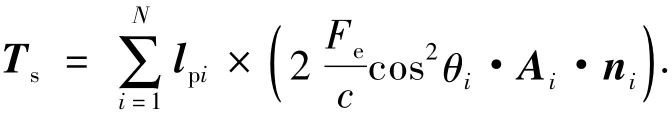
式中:Fe为太阳辐射通量(=1 358 W/m2);c为光速;N为受晒面个数;Ai为第i个受晒面面积;θi为第i个受晒面入射角;ni为第i个受晒面内法向单位矢量;lpi为整星质心到第i个受晒面的辐射压力中心的矢径．

2.5 敏感器的建模

如上所述，所研究的航天器装配了速率陀螺、地球敏感器、太阳敏感器及星敏感器等测量设备.现有文献中对于各种敏感器的建模已有大量论述，本文利用Modelica语言进行编写，以实现各种敏感器的功能，主要依据为文献［11］和［12］.

2.6 航天器姿态及轨道控制系统AOCS的建模

姿态及轨道控制分系统具备如下功能:消初偏;姿态确定;姿态稳定与控制;姿态机动;安全管理.为实现如上功能，AOCS由如下几个软件模块组成:工作模式管理、姿态确定、姿态控制、卸载逻辑组成.

航天器的主执行机构为三轴正交安装+一等倾角斜装，标称状态下各轮按偏置动量运动，但整星在标称状态下处于零动量.采用PID+前馈补偿的策略，控制律如下:

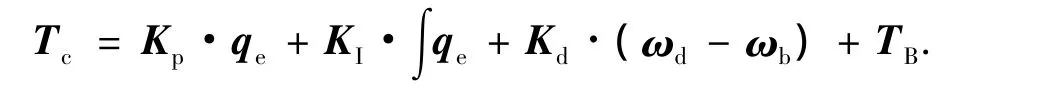
式中:Kp、KI、Kd分别为控制器的比例、积分、微分控制参数;qe为姿态四元数误差;ωd为期望的姿态角速度;ωb为实际(通过姿态敏感器测出)角速度;TB为补偿力矩;Tc为期望的作用于航天器的控制力矩．

磁力矩器用于对飞轮进行卸载.根据飞轮所需卸载的角动量，按下式产生控制力矩:

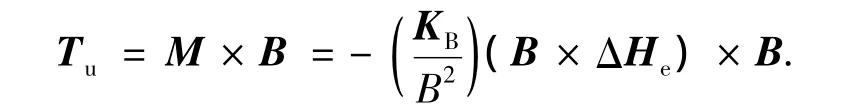
其中:M为磁矩矢量;B为地磁场强度矢量(B为B的模);KB为磁控参数;ΔHe为所需要卸载的角动量．因此，磁力矩器的控制电压为UB=KuBTu，其中KuB为磁力矩器的电压磁矩系数．

3 仿真研究

建立了航天器的多领域模型后，可对航天器的各种姿态控制模式进行仿真.限于篇幅，本文给出2种典型模式下的姿态控制仿真:入轨后三轴对地稳定姿态建立，以及三轴姿态大角度机动.

3.1 仿真参数

轨道为太阳同步轨道圆轨道，轨道高度600 km，轨道倾角97.764°，轨道周期96.54 min，降交点地方时为6:30 AM.航天器系统质量1 000 kg，主体尺寸为1.2 m×1.2 m×1.2 m，质心在其本体坐标系下坐标rcm=［0.6 0 0］T．航天器系统相对于其质心坐标系的转动惯量矩阵为

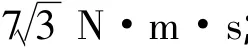
3.2 航天器入轨后三轴对地稳定姿态建立的仿真

0假设航天器入轨后的三轴姿态偏差及稳定度分别为(姿态角和角速度单位分别为(°)和(°)/s)

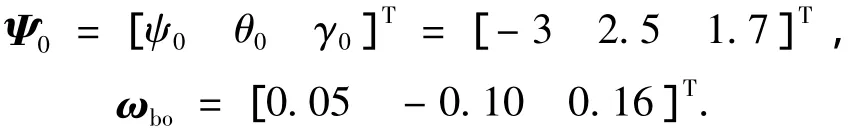
其中:ψ、θ、γ分别为偏航角、俯仰角及滚转角偏差;ωbo为航天器本体系相对于轨道系的旋转角速度在本体系下的投影．

利用上面建立的多领域模型对航天器建立三轴对地姿态的过程进行仿真(仿真了1000 s).仿真结果如图4～5所示.其中，图4～5分别为三轴姿态和角速度变化曲线，仿真结果表明，在60 s时，三轴姿态精度已经达到［－0.071°0.042°－0.043°］T，姿态角速度达到［0.010(°)/s －0.007(°)/s －0.005(°)/s］T，而长期对地姿态精度和角速度达到了［－2.0×10－33.4×10－3－4.5 ×10－4］T(单位:(°))和［1.75 ×10－52.36 ×10－6－3.86 ×10－6］T(单位:(°)/s).

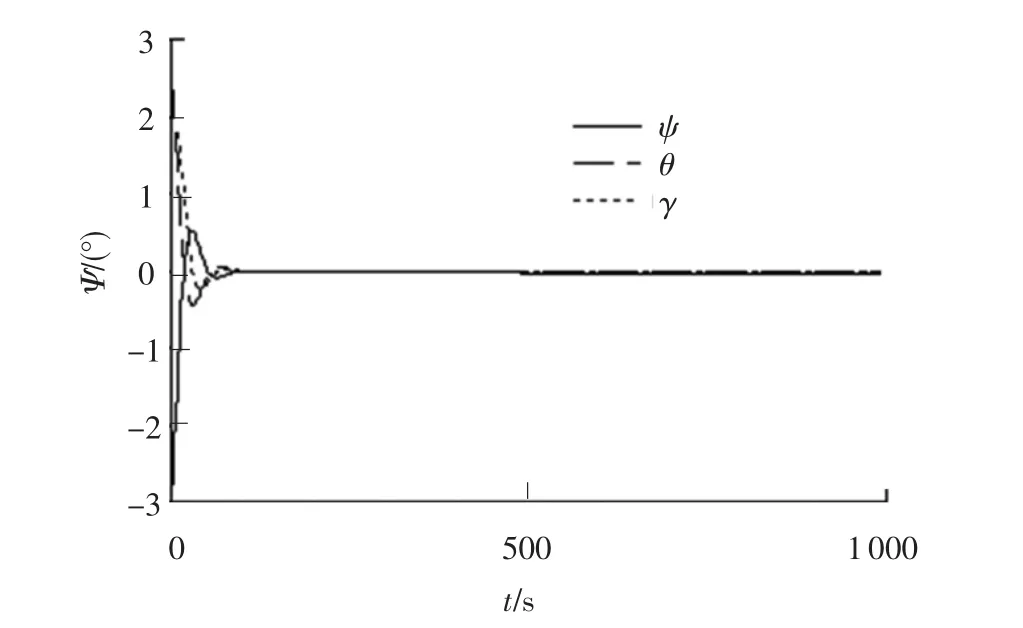
图4 航天器对地稳定姿态的建立

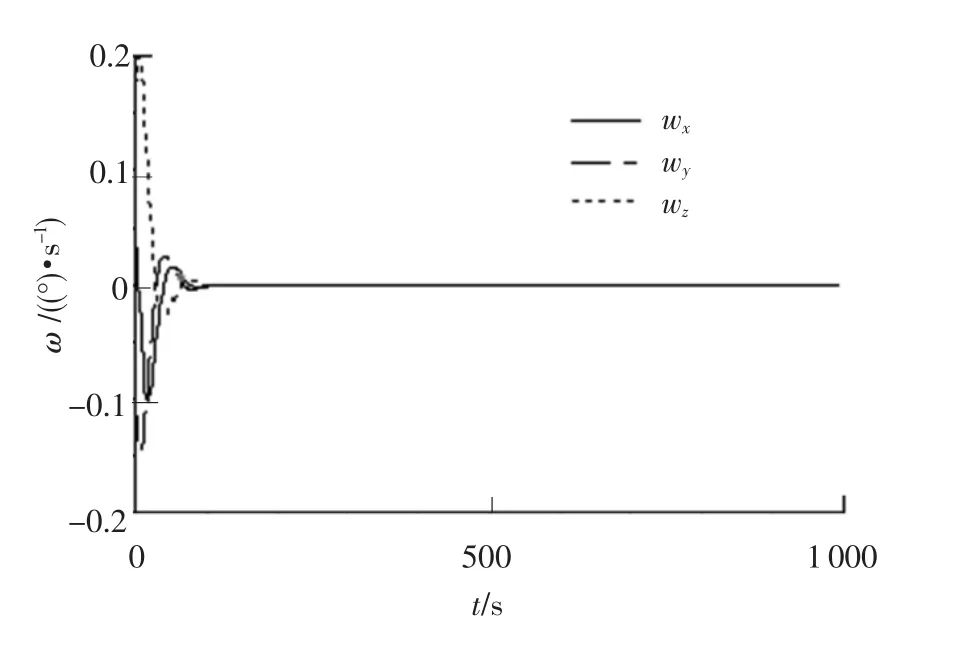
图5 航天器角速度变化曲线

3.3 航天器三轴姿态机动的仿真

姿态机动也是航天器的常用模式之一，在此利用所建的多领域模型对其过程进行仿真.假设卫星初始处于三轴对地姿态，现要求各轴进行三轴姿态机动，每个轴分别偏转 10°、－10°、15°.即初始时刻航天器姿态角、角速度近似为 0，即Ψ0≈ω0≈ 0，而机动后的姿态角 Ψf=［10° －10° 15°］T，角速度ωf≈ 0，机动时间tf=100．

图6为姿态机动过程中期望姿态和实际姿态的变化曲线(需要指出的是，仿真中给出了0～200 s的数据，其中100 s内为机动时间，100 s后为姿态保持，即姿态期望值不变).仿真结果表明，姿态机动结束后，姿态稳定(200 s时刻)时姿态角和角速度为

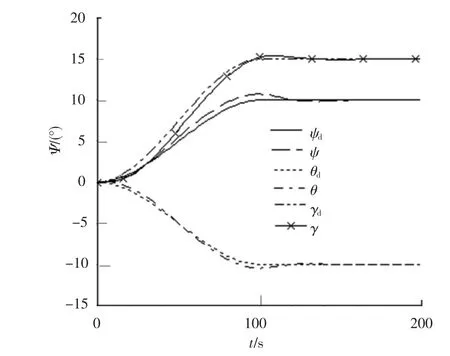
图6 姿态机动中姿态的变化曲线

4 结论

多学科设计优化技术的兴起，使得多领域统一建模成为大势所趋.航天器系统的建模涉及到机械、电气、控制、软件等多个领域，为真实反映系统的状态，本文建立了包括姿轨控分系统(软件)、飞轮控制器(控制)、飞行机构(电机及其驱动器)、磁力矩器、姿态动力学、轨道动力学等的多领域模型.模型中的各模块具有可重用性，用户根据需要可方便的建立各种对象的多领域模型，实现各种姿态控制模式的仿真.开发航天器系统的多领域统一建模与仿真平台，对于未来的型号研制具有极其重要的意义.未来的工作将继续完善各种敏感器、执行机构的建模，以及编写多种控制算法，并实现航天器跟踪、接近过程的建模和仿真.

［1］SAMIN J C，BRÜLS O，COLLARD J F，et al．Multiphysics modelingand optimization ofmechatronic multibody systems［J］.Multibody System Dynamic. 2007，18(3):345 －373.

［2］SOBIESZCZANSKI J，HAFTKA R T.Multidisciplinary aerospace design optimization:Survey of recent developments［J］.Structural and Multidisciplinary Optimization， 1997，14(1):1 －23.

［3］宋其江，宋敏强，王日新.基于MAS的航天器故障诊断系统模型［J］.吉林大学学报(工学版)， 2009，39(2):546－550.

［4］XU W F，LIU Y，LIANG B，et al．Unified multi－domain modeling and simulation of space robot for capturing a moving target［J］.Multibody System Dynamics. 2010，23(3):293－331.

［5］LOVERA M.Control－oriented modelling and simulation of spacecraft attitude and orbit dynamics［J］.Mathematical and Computer Modelling of Dynamical Systems. 2006，12(1):73－88.

［6］SONG B，MA G F，LI C J.Adaptive variable structure control based on backstepping for spacecraft with reacti on wheels during attitude maneuver［J］.Journal of Harbin Institute of Technology(New Series)， 2009，16(1):138－144.

［7］野姜，胡庆雷，马广富.挠性航天器姿态机动智能变结构输出反馈控制［J］.哈尔滨工业大学学报， 2009，41(3):1－5.

［8］SANYAL A，FOSBURY A，CHATURVEDI N，et al．Inertia－free spacecraft attitude tracking with disturbance rejection and almost global stabilization［J］.Journal of Guidance，Control，and Dynamics， 2009，32(4):1167－1178.

［9］YOON H，AGRAWAL B N.Novel expressions of equations of relative motion and control in keplerian orbits［J］.Journal of Guidance，Control，and Dynamics. 2009，32(2):664－669.

［10］李太玉，张育林.利用地磁场给飞轮卸载的新方法［J］.中国空间科学技术，2001(6):56－61.

［11］刘良栋.卫星控制系统仿真技术［M］.北京:宇航出版社，2003.

［12］屠善澄.卫星姿态动力学与控制［M］.北京:宇航出版社，2002.

Development of united multi-domain modeling and simulation platform for three-axis stabilized spacecrafts

XU Wen－fu1，2，LIANG Bin1，LI Cheng1

(1.Shenzhen Graduate School，Harbin Institute of Technology，518055 Shenzhen，China，wfxu@hit.edu.cn;2.Shenzhen Aerospace Dongfanghong HIT Satellite Ltd.，518057 Shenzhen，China)

In order to reflect the control characteristics of a spacecraft under the interaction between many disciplines，a multi－domain modeling and simulation platform，dealing with mechanics，electricity，control，software，et al.is developed.This platform is composed of the following modules:the attitude control software，the flywheel system(including motor and its driver，bearing friction，the mechanism of the flywheel et al.)，magnetotorquers，attitude sensors，attitude dynamic，orbital dynamic and environment torques，and so on.All the modules are realized using Modelica language，and integrated into an organic whole.The simulation of two typical attitude control modes—attitude established and attitude manoeuvre shows that，this simulation platform is not only used to analyze the control performance of the closed－loop system，but also to evaluate the effect of each domain＇s devices.Sufficient application of this platform during all the phases(project proposal，subsystem，system，et al.)can attain the purpose of Multidisciplinary Design Optimization.

spacecraft;multi－domain modeling;simulation;three－axis stabilization;attitude control

TP24

A

0367－6234(2011)07－0074－07

2010－03－10.

国家自然科学基金资助项目(60805033).

徐文福(1979—)，男，副教授.

(编辑 张 宏)