涌现计算概述
张江
涌现计算概述
张江
(北京师范大学 管理学院系统科学系,北京 100875)
通过4个实例:蚁群最短路径算法、粒子群优化算法、一维元胞自动机和粘菌的涌现计算,阐述了涌现计算的基本思想和方法,并对涌现计算中的一些问题进行了总结与展望.
涌现;涌现计算;复杂系统;多主体模拟
传统的计算模式大多是一种串行的、中心控制式的,例如图灵机仅有一个读写头在工作,每一个时刻只能完成一步运算[1].计算机理论科学家们已经证明这种串行机器在原则上能够模拟一切计算,甚至包括大规模的并行运算装置,前提是我们对效率没有任何要求. 然而,在现实世界中,效率是一个非常重要的问题,利用大量的并行空间换取运算时间是更重要的问题. 随着计算机网络以及存储设备的大量普及,到了20世纪末期,人们越来越重视这种去中心化的、并行的运算模式. 在复杂性科学研究中,人们甚至为这些新的运算模式取了一个好听的名字:涌现计算.
涌现(Emergence),字面翻译为突然出现,在系统科学中它意味着“整体大于部分之和”. 任何系统都是由大量微观元素构成的整体,这些微观个体之间会发生局部的相互作用,然而当我们把这些个体看作一个整体的时候,就会有一些全新的属性或者规律或者模式自发地冒出来,那么这种现象就被称为涌现[2]. 本文通过若干涌现计算的例子,让读者真正领会涌现是一种非常强大的资源,可以用来解决各式各样的实际问题,同时也指出这种方法的一些不足之处.
1 以蚂蚁觅食为例简介涌现与涌现计算
一个涌现的实例来自蚂蚁王国[3]. 我们都知道,每只小小的蚂蚁都是一个非常简单的个体,它们没有聪明的头脑,只会完成一些简单的计算任务. 然而,当把成千上万只小蚂蚁组合到一起的时候,整个蚁群就能表现出非常复杂、庞大的涌现现象,如社会分工、集体协作等等.
例如在蚂蚁觅食的活动中,它们就能表现出涌现的行为. 我们知道,单个的蚂蚁体形弱小,它们的视力范围非常有限,只能看到邻近的景物. 然而,当大量的蚂蚁共同协作的时候,它们通过相互作用传递信息,就可以发现一条最快的搬运食物回巢的路线,这条最快的搬运路径就是典型的蚂蚁群体的涌现行为. 事实上,在这群蚂蚁中,并没有哪个蚁王或者蚁后对整队蚂蚁发号施令,所有的涌现行为全部是这群蚂蚁局部相互作用的结果.
将涌现的思想借鉴到计算系统便构成了涌现计算的想法. 从计算的观点来看,一个涌现系统其实就是一个并行计算的系统. 蚁群中的单个蚂蚁是一个小型处理器,它们可以并行地、局部地完成计算任务,而蚁群则可以通过集合这些并行处理单元来完成复杂的运算任务,如寻找有效的搬运食物路径或者形成复杂、好看的图案. 我们完全可能设计一个人工计算系统,通过模拟简单的并行计算单元实现对整体涌现系统的模拟,如我们可以把蚁群觅食的例子用计算机模拟出来,具体见图1.

图1 蚂蚁觅食的计算机模拟
在一个二维的离散化的网格世界里,我们可以用一个计算机程序体(称之为Agent)来模拟一只觅食的蚂蚁. 这只蚂蚁可以从自己的巢穴出发,在这个网格世界中随机游走. 如果它找到了食物就开始往回折返,为了呼唤其他蚂蚁过来,它会在经过的格子中撒下信息素(图1b)中的彩色方格). 其他的蚂蚁在随机游走的过程中,如果碰到了彩色方格(闻到了信息素的味道)就会沿着信息素的浓度向前爬行,直到找到食物. 一旦它找到食物又会进一步向环境播撒信息素. 这样,一旦有一只蚂蚁找到了食物,就会吸引更多的蚂蚁过来. 同时,信息素还会在环境中慢慢地挥发、褪色,这样,没有蚂蚁经过的那条路径就会逐渐耗散它的信息素,渐渐地,只有那条最短的路径聚集了最多的蚂蚁,蚂蚁群体们通过相互作用找到了通向食物最短的路. 所有这些现象完全可以在计算机模拟世界中计算得到,因此,我们说,涌现是可以通过多主体计算进行模拟的.
由于涌现的系统有很多优越特征,例如它的抗干扰能力、创新性等;所以,人们感兴趣的是另外一种思路,也就是我们给系统预设一个具体的计算目标,但是这个计算目标不是通过传统的编程直接告诉计算机如何实现,而是通过设计一种微观个体的相互作用规则,从而让最终的目标自发地涌现出来. 也就是说,如果某系统的涌现行为或者属性可以看作是某种计算的话,那么我们就称这个系统正在执行涌现计算[4].
涌现计算与涌现的模拟有很大的相似性,它们都是利用计算系统实现系统的涌现现象,但是二者又有很大的不同. 涌现的模拟旨在用计算机模拟一个真实的系统,使得这个模拟具备某种涌现的特征;而涌现计算则要求更高:该系统不仅需要具备涌现特征,这种涌现特征还要能完成某种特定的计算任务. 也就是说,涌现模拟是利用个体的简单计算而实现涌现,涌现计算则要求系统的涌现完成实际的计算.
让我们再回到蚂蚁的例子上来,虽然我们已经可以把蚁群的行为和涌现属性用计算机模拟出来,但这个模拟系统并不能帮我们执行有意义的计算. 转机出现了,1992年Marco Dorigo在他的博士论文中提出了蚁群优化算法[5](Ant Colony Optimization):通过改造蚂蚁的模拟程序的确找到了一条真实地图上的最短路径(具体参见文献[6]). 这是一种典型的涌现计算的例子,作为一种涌现的结果,这条最短路径是被涌现计算出来的.
进一步,蚁群优化算法还可以用来解决包括旅行商问题、组合优化问题等更一般的问题. 这也就体现了涌现计算的强大优势.
2 3种涌现计算实例
2.1 粒子群优化算法
1986年,计算机科学家Craig Reynolds发明了一种被称为Boid的计算机模拟程序. 通过给计算机中的智能体(Boid)设置3条简单的规则:靠近、对齐、避免碰撞,Craig就能活灵活现地模拟出鸟类群体的飞行行为[7]. 然而,早期的Boid仅仅能够逼真地模拟实际的鸟类飞行情况,如果我们在Boid所处的人工环境中加入食物会出现什么情况呢?在真实世界中,鸟类会争先恐后地奔向食物. 假如我们在Boid飞行的环境撒上很多食物,颜色深的地方表示食物浓度大,浅的地方浓度小,那么Boid就应该会自动聚集在食物浓度较大的地方.
能不能用鸟类飞行觅食的行为来解决实际的优化问题呢?我们仍然采用比喻的方法,把人工Boid飞行的空间比喻成优化问题的解空间,把优化函数的函数值比喻成食物的浓度. 这样,优化函数值越大的地方对应的食物越多,Boid飞向这个点的概率就会越大. 最后,很有可能所有的Boid都集中到了目标函数值最大的点,从而利用Boid群体的涌现行为求解了函数优化的问题.
这实际上就是粒子群优化算法(Particle Swarm Optimization,简称PSO算法)的思路. 在PSO算法中,一群虚拟的粒子(就相当于是Boid)在优化空间中自由飞翔,它们会寻找食物并聚集到食物最多的点从而完成优化任务. 如果某个特殊的Boid在问题空间中发现了一个食物浓度更高的点,它就会召集其他的Boid过去. Boid在飞行的过程中会经历一些小的干扰,这样就会使有些Boid在飞行的过程中发生与原轨道的较小偏移,从而使得Boid群体具有了一定的创新性.

图2 PSO算法优化函数的动态展示

2.2 一维元胞自动机的涌现计算
为了更好地理解涌现计算是怎样在计算机中发生的,Jims Crutchfield[9]用一类最简单的涌现系统:一维的元胞自动机来实现涌现计算. 由于一维的元胞自动机是一类典型的通过局部相互作用生成复杂的全局模式的系统,所以,细致分析这类系统往往能够让我们对系统的运作机理有更好的了解.
所谓的一维元胞自动机是一个一维的方格世界,如图3所示. 其中每一个方格(元胞)是由黑白两种颜色构成的,并且每个元胞下一时刻的颜色仅仅由它左右两侧元胞的颜色决定. 我们知道,每个元胞的颜色只有黑白两种,这样,任意一个元胞加上它左右两个元胞的颜色组合就一共有8种情况:黑黑黑、黑黑白,黑白黑、白黑黑、黑白白、白黑白、白白白. 只要我们为这8种情况下的每一种都指定当前元胞在下一时刻的颜色,那么就完全定义了这个一维元胞自动机的规则.

图3 一维元胞自动机
我们可以用一张二维图形来展现一维元胞自动机的运行情况,如图4所示. 图4a)中,每一个横行表示这个元胞自动机在某一时刻的状态,从上往下则表示时间运行的状态,每一个元胞都根据它左右两个邻居的颜色进行自己颜色的更新. 元胞自动机的动态展现二维图如图4b)所示.

图4 一维元胞自动机的运行
一维的元胞自动机完全是一个确定性的系统,由于规则是固定的,这样,只要给定初始状态(第1行的黑白排列情况),那么元胞自动机所画出的图像就是固定的.
我们完全可以把这个元胞自动机看作是一个计算系统,只要我们把该自动机的初始条件看作是这个元胞自动机的输入数据,而把运行比如说100步之后的黑白元胞的分布情况看作它的计算结果,那么给定一组输入条件之后,这个元胞自动机就会完成一系列局部的操作,最终在第100步的时候给出一个结果. 当元胞自动机的规则确定之后,不同的输入一般会对应不同的输出结果. 但问题是,一般情况下,这个元胞自动机不会进行有意义的运算,因为它的规则太任意了.
能不能设计某种非常简单的计算任务,从而在各种各样的元胞自动机(规则不同)中找到一种合适的自动机来完成指定的计算任务呢?Crutchfield运用遗传算法对所有可能的一维元胞自动机进行搜索,通过不断进化,系统终于找到了一些能完成简单运算的元胞自动机. 比如,Crutchfield设计的一个简单的运算任务就是对初始的黑白元胞的比例进行分类. 如果初始条件下,黑色的元胞偏多一些,元胞自动机100步后的输出就必须全部都是黑色元胞;反之,则要求元胞自动机在100步后全部输出白色. 这样,如果我们把初始的黑白元胞看作输入,把100步后的结果看作输出,那么这个一维元胞自动机就能够完成密度分类这个简单的任务[10],如图5所示.
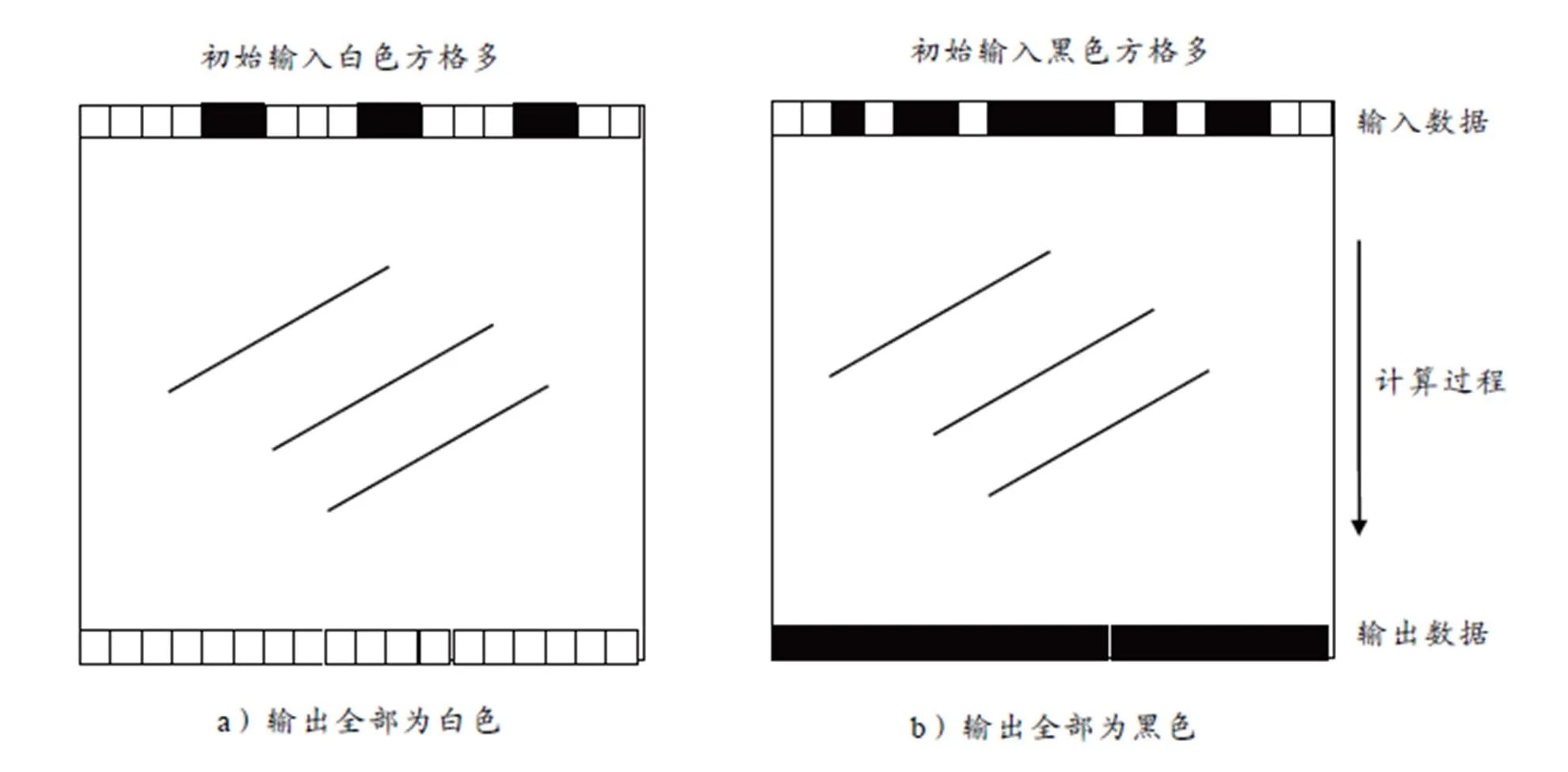
图5 一维元胞自动机完成密度分类任务
这个任务表面上看起来很简单,然而对于元胞自动机来说却非常难. 因为每个元胞只能跟它左右两个邻居通信而看不到输入时候的整体情况. 在计算过程中,每一个元胞也只能根据左右邻居的颜色机械地按照固定的规则变换颜色,不存在某个超级元胞能够对所有的元胞发号施令以决定系统的运行. 也就是说,这群元胞必须学会相互协调合作才能完成对于它们来说非常复杂的任务.
然而,通过遗传算法,Crutchfield终于找到了这种能够完成密度分类任务的一维元胞自动机. 6a)图的初始黑色元胞密度为0.48,该元胞自动机正确给出了全部是白色的答案;6b)图的初始密度为0.51,该元胞自动机正确给出了全部黑色的答案.
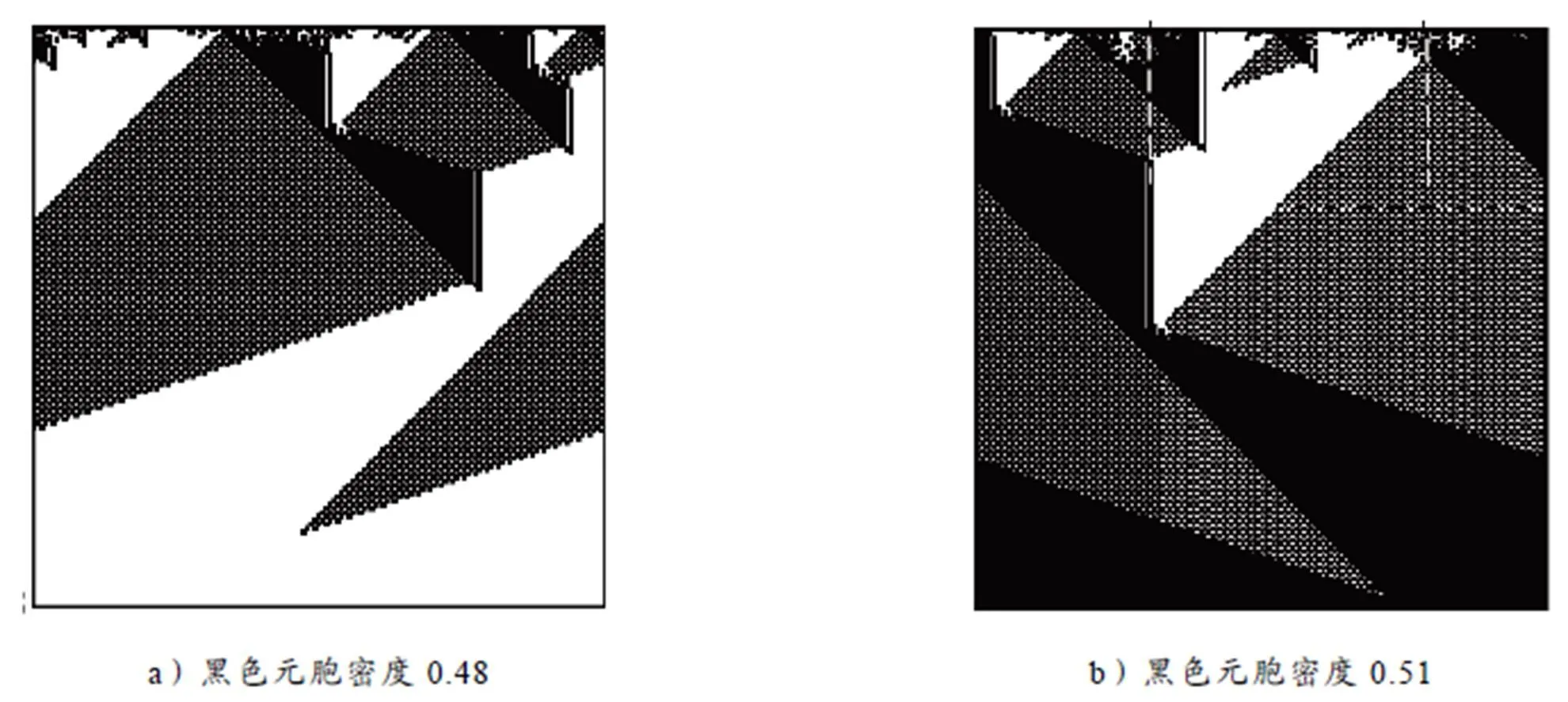
图6 用遗传算法找到的可以成功分类初始元胞黑色密度的自动机
遗传算法终于找到了可以正确分类的元胞自动机,那么究竟这些简单的自动机是如何完成这种复杂的计算任务的呢?Crutchfield进一步研究发现,这些成功分类的自动机的运行图都具备一种明显的特征:有很多横框区域的大斜线,以及一些明显的三角形块状区域. 我们知道,在元胞自动机的运行图中,一条黑色的斜线就相当于一个传播的信号(黑色元胞的信息从一侧传递到另一侧). 也就是说,这些元胞之间会建立一种相互通信的机制. 当初始的某一个区域有更多的黑色元胞的时候,在这些元胞的边界出就会产生某种“粒子”(有一些传播的元胞组成),从而与白色元胞区域产生对消的现象. 这样,通过不断的“粒子对消”完成了黑色元胞数与白色元胞数的比较,最后输出正确的运算结果.
为了看清楚这些简单的元胞自动机的运行原理,Crutchfield甚至过滤掉了那些规则的三角块区域,而把边界的“粒子”凸现出来(图7). 我们看到,这些粒子(标为希腊字母的线条)在时空中运动,把信息从世界的一端传递到另一端,并与其他的粒子相互碰撞、反应,生成其他的粒子或者湮灭,从而完成对于这些元胞自动机来说非常复杂的计算任务.

图7 “粒子碰撞”图
总结来看,Crutchfield所研究的演化元胞自动机属于一类涌现计算模型,每个元胞都只能完成简单的局部运算,但是这些元胞通过相互作用完成了全局的运算. Crutchfield的研究进一步指出,这些简单的并行相互作用的元胞之所以能够完成全局运算,其中一个最重要的因素就是它们可以通过“粒子”进行跨区域的通信,从而使不同区域的两个或多个元胞之间能够发生相互作用而实现整体的协调与合作.
Crutchfield的研究指出,涌现计算的一个重要的必要条件就是:信息的流动. 只有信息的流动才能完成不同区域的通信,从而真正让本来相互分散的个体连接成一个整体.
2.3 粘菌的涌现计算
之前提到的各种涌现计算或者对涌现的模拟都是在计算机中完成的,下面看一个发生在现实世界中的涌现计算的例子.
2010年1月,著名科学杂志《Science》刊登了一篇题名为Rules for Biologically Inspired Adaptive Network Design的文章,作者是来自日本北海道大学的Tero等教授. 他们利用现实世界的一团粘菌(俗称鼻涕虫,一种粘菌门的组织,生长在腐烂的植物或潮湿的地面上,英文名字为Slime mold)设计了一条连通东京及其附近城市的铁路网[10]!这是一次别开生面的涌现计算!
粘菌是一群裸露的无细胞壁多核的原生质团,它们可以通过连续的形变而缓慢移动,当这团裸露的细胞在空间上遇到多个分散的食物源的时候,就会构建起一些运输营养的通道. Tero等教授正是利用了粘菌的这种天性,在实验室中为粘菌们设计了一套人工食物源环境,让这群简单的原生质团形成了运输营养的网络. 他们将一张东京以及附近城市的地图作为粘菌生长的环境,在初始时刻,让粘菌集中在地图上的东京点,接着在地图东京附近的城市放上粘菌喜欢吃的食物,然后让这群粘菌在实验地图上缓慢变形、游走. 起初,这群简单的细胞群体在地图上扩散,几个小时后,当它们遇到了食物之后就开始精炼这些模式而形成若干运输食物的隧道;再经过几个小时后,一些较大的运输隧道开始慢慢成长,而更多的小型隧道逐渐消失;最终,只有几个主干隧道保留了下来. 经过一天多的时间,它们最终演化出了一条条营养运输网络 .
实验人员将粘菌构建的食物运输网络与现实的东京附近的地铁网络进行比较,发现这两种网络非常相似,如图8所示.

图8 粘菌计算出的运输网络与东京附近城市的铁路网络对比①
图8向我们展示,两个网络无论在结构还是形状上都非常相似. 也就是说,这群看起来笨拙无比、没有任何智力可言的粘菌的确完成了可观的计算任务:修筑轨道网络. 更有趣的是,为了修建这样一套有效率的网络运输系统,被称为灵长类动物之首,号称具有超凡智力的人类设计师也要花费数十年的时间.
就这样,这些简单得不能再简单、低级得不能再低级的粘菌通过简单的相互作用就在整体上实现了一次可观的涌现计算.
3 讨论
在领略了各式各样的涌现计算的实例之后,我们一定会感叹大自然的鬼斧神工,原来简单的计算机程序或者是粘菌竟能完成如此复杂的运算任务. 然而,涌现与计算这个课题才刚刚开始,我们对于涌现和计算还知之甚少,由涌现计算引发的一些问题需要思考.
3.1 永恒的新奇与开放式结局
我们曾指出,涌现是指一种不能够还原成底层的高层属性或者现象,尤其是对于计算系统来说,人们更希望系统能够自发冒出来一些设计者意想不到的新奇属性. 著名的系统科学家John Holland(遗传算法之父)曾用“永恒的新奇性”(Perpetual Innovation)一词来描述人们希望实现的真正的涌现计算系统.
我们都知道,自然界的进化现象是生生不息、永无休止的. 一个物种灭绝了,总会伴随着新的物种出现,更有趣的是,进化还会产生于多个层面上. 宇宙的演化用了大约150亿年的时间,而地球上的生命演化则仅仅用了40多亿年的时间;人类出现之后,文明的进化却仅用了将近5 000年时间. 在每个层面上,复杂性和新奇性不断产生,进化永无休止.
在涌现计算中,程序员希望他们设计的系统能实现一种所谓的开放式结局进化(Open Ended Evolution). 即进化能够永无休止地运行下去,一些新的属性和现象能从系统中冒出来. 开放式结局一直是程序设计者追求的目标之一,但多年来一直没有实现. 这是为什么呢?有没有理论上的解答呢?
3.2 涌现计算与尺度
有人说,之所以我们没有看到永恒的新奇和开放式结局,是因为我们没有给人工涌现系统提供足够大的演化空间和足够长的演化时间. 大自然进化出生命都用了数十亿年的时间,凭什么要计算机仅仅用几个小时或者几天就演化出堪与自然界相比的复杂性呢?正如J.Gonway指出的,“只要给我足够大的方格空间,并等待足够长的时间,从原则上讲,‘生命’(一种特殊的二维元胞自动机模型)游戏中可以创造任何你想要的东西,包括宇宙天体、进化的生物,甚至是可以撰写Ph.D论文的智慧生命”. 但关键问题是,我们到底需要多大的空间和多长的时间呢?
有人曾作过粗略计算:如果每个方格占用一个屏幕像素大小的空间,那么要在“生命游戏”中实现一个能够完成自我复制的原始生命,就至少需要整个纽约市那么大的屏幕!可问题是,人类愿意设计这么大规模尺度的计算系统吗?这样的计算模拟系统有意义吗?这也为我们提出了一个非常重要的理论问题:涌现计算和系统的尺度(空间上、时间上)到底有什么关系?分形的研究告诉我们,很多复杂系统都会展现出一种无标度的特征. 也就是说,无论你从哪一个尺度去观察一个复杂分形系统,都会发现它们是相似的. 如著名科学家Manderbrolt就曾指出,用不同单位的尺子去测量英国的海岸线,会得到完全不同的总长度. 这是因为海岸线是一个分形,随着观测尺度越来越精细,海岸线本身也会展现得越来越复杂,你完全找不到一种特征尺度能够最好地刻画复杂的分形.
因此,在计算系统中,我们也可能根本找不到一种所谓的特征尺度(空间或者时间),来最好地模拟大自然的永恒新奇和开放式结局进化现象. 这是因为,大自然系统总是会随着我们描述、模拟它的精度变大而不断冒出各种复杂性. 但是无论计算系统多大,它总归是有限的,是具备特征尺度的. 所以,这类系统永远也不会实现而只能无限逼近永恒的新奇与开放式结局. 这也仅仅是笔者的猜测之一,诸如尺度、分形、涌现等问题还需要更细致的分析研究.
3.3 涌现计算的语义与观察者
虽然涌现计算在很多不同领域如人工模拟的蚂蚁、真实的粘菌获得了成功,但是,回想这些成功的案例,它们几乎是一个例子一种设计,没有什么共同性可言. 当面临一个崭新的任务时,除了进行反复的实验,我们仍然不能遵循一些规律直接设计出一种涌现计算系统. 这其中的一个关键问题就在于:计算系统需要在高层次与设计者进行语义上的沟通,从而按照设计的模式去演化.
通常来讲,我们给定计算机一组局部作用规则,让它们在计算机中相互作用、演化是很容易的,这种系统必然会演化出一种整体的模式(例如元胞自动机). 但问题的难点在于,这种整体模式对于我们观察者来说往往是没有任何意义的. 所以,涌现计算要解决的一个关键性问题就是如何在杂乱无章的整体模式与观察者可理解的意义之间建立起一种联系.
演化的元胞自动机模型部分地回答了这个问题. 我们需要一种从观察者到系统整体,再从系统整体到系统局部的反馈机制. 也就是说,由观察者来判断系统整体行为的语义(例如元胞自动机能不能对初始方格进行密度分类),之后系统按照观察者赋予的意义进行演化(遗传算法). Crutchfield的研究指出,这种高层次的行为又会反馈给具体的元胞,并在它们之间产生一种信号传递机制,从而完成我们要求的涌现计算.
另外一种解决途径来源于粘菌的涌现计算例子. 在这里,我们仍然需要与涌现系统建立某种高层次的语义联系,但是改变的不再是系统,而是观察者本身. 对于粘菌来说,它们自身的规则始终没有改变过,它们只知道在低层次寻找食物. 然而,我们观察者理解了粘菌的习性,于是通过设计食物的摆放位置(观察者的行为),从而诱导出了粘菌涌现计算的整体意义.
[1] LEWIS H R, PAPADIMITRIOU C H. Elements of the theory of computation[M]. New Jersey: Prentice-Hall Inc,1998.
[2] 约翰·霍兰. 涌现:从混沌到有序[M]. 上海:上海科学技术出版公司,2006.
[3] 李建会,张江. 数字创世纪:人工生命的新科学[M]. 北京:科学出版社,2006.
[4] FORREST S, HOFMEXR S A, SOMAYAJI A. Emergent computation[M]. Herausgeber: MIT Press, 1991.
[5] DORIGO M. Optimization, learning and natural algorithms[D]. Milano: Politecnico di Milan, 1992.
[6] 王旭,张江,崔平远. 一种基于蚁群算法求解路径规划问题的新方法[C]//2003年中国智能自动化会议论文集:下册,2003: 996-999.
[7] REYNOLDS C W. Flocks, herds and schools: a distributed behavioral model[J]. Computer Graphics, 1987, 21(4): 25-34.
[8] KENNEDY J, EBERTHART R. Particle swarm optimization[C]//IEEE Transations, 1995: 1942-1948.
[9] CRUTCHFIELD J P, MITCHELL M, DAS R. The evolutionary design of collective computation in cellular automata[M]//Evolutionary dynamics exploring the interplay of selection, neutrality, accident, and function. New York: Oxford University Press, 2002.
[10] TERO A, TAKAGI S, SAIGUSA T, et al. Rules for biologically inspired adaptive network design[J]. Science, 2010, 327: 439-442.
[11] 米歇尔·沃尔德洛普. 复杂:诞生于混沌与秩序边缘的科学[M]. 北京:生活、读书、新知三联书店,1997.
①图片参见http://www.wired.com/wiredscience/2010/01/slime-mold-grows-network-just-like-tokyo-rail- system/
Introduction to Emergent Computation
ZHANGJiang
(Department of Systems Science, School of Management, Beijing Normal University, Beijing 100875, China)
This paper introduces a new paradigm of computation emergent computation, which takes advantage of parallel computing of a large number of interacting individuals to process some complicated computational tasks. It presents the basic ideas and methods of emergent computation by four instances: ant colony shortest path finding, particle optimization algorithm, one-dimensional evolutionary cellular automata and the natural computing of the real slime molds. Finally, it summarizes some questions and the prospects of the emergent computation.
emergence; emergent computation; complex systems; multi-agent simulation
1006-7302(2011)04-0029-09
N941.1
A
2011-07-20
张江(1978—),男,北京市人,博士,中科院数学与系统科学所博士后,研究方向为系统理论与复杂性研究.

