元胞自动机研究进展

孙德山



元胞自动机研究进展

孙德山

（辽宁师范大学 数学学院，辽宁 大连 116029）

元胞自动机是一个具有简单运算规则的动态模型，但却能展现出复杂的行为. 元胞自动机引起了许多研究者的关注，相关研究工作已经广泛展开. 论文综述了元胞自动机的研究进展及在不同领域的一些应用.

元胞自动机；元胞空间；复杂系统

1951年，Von Neumann给出了元胞自动机（Cellular Automata，CA）模型，又称为细胞自动机. 元胞自动机在时间和空间上是一个离散的动力系统，目前已经成为复杂系统建模的主要工具[1]. 元胞自动机可以看成是由许多网格组成的，网格中的每个单元为一个元胞，只取有限的离散状态，它们都遵循同样的局部变换规则，并进行同步更新；大量元胞通过简单的相互作用形成系统的动态演化，并能形成复杂的演化状态；元胞自动机不是由确定的函数定义，而是由简单的规则决定. 即，元胞自动机模型是满足一定规则的动力系统的总称，每个变量的状态只取有限多个，并且状态改变的规则都是局部的. 本文介绍元胞自动机的构成原理、研究进展以及在不同领域中的应用.

1 元胞自动机的基本组成

元胞、元胞空间、邻居及规则就构成一个元胞自动机. 元胞自动机最基本的组成单位是元胞，元胞位于离散的一维、二维或多维空间的网格点上. 元胞的状态可以由{0,1}组成，也可以是整数形式的离散集. 元胞所分布的空间网点集合称为元胞空间，其几何划分可以是任意维数的欧几里得空间划分. 一维和二维元胞自动机是目前研究的重点. 一维元胞自动机的元胞空间划分只有一种形式，二维元胞空间的划分很灵活，可按三角形、四方形或六边形3种网格排列.

元胞空间可以在各维上无限延展，这有助于在理论上进行研究，但是这一理想条件无法在实际应用中实现，因此，定义不同的边界条件显得非常重要. 边界条件一般有3种类型：反射型、定值型和周期型. 有时，可以采用随机型来模拟实际的自然现象，即实时在边界生成随机数.

以上的元胞及元胞空间只表示了系统的静态成分，将演化规则加入后就形成了动态系统. 元胞自动机中的这些规则是在局部空间范围内定义的，一个元胞将根据自身的状态和它的邻居元胞的状态决定其下一时刻的状态；因此，定义邻居规则是元胞自动机运行的前提，必须明确一个元胞的邻居有哪些. 一维元胞自动机根据半径来确定邻居. 二维元胞自动机定义邻居比较复杂，一般采用如图1所示的2种形式. 图1中，中心元胞用黑色表示，其邻居元胞用灰色表示，中心元胞在下一时刻的状态是根据自身状态和邻居的状态来计算.

图1a）是冯·诺依曼型邻居，此时元胞的邻居由上、下、左、右相邻的4个元胞组成，邻居半径为1. 图1b）是摩尔型邻居，此时元胞的邻居由上、下、左、右、左上、右上、右下、左下8个元胞组成.

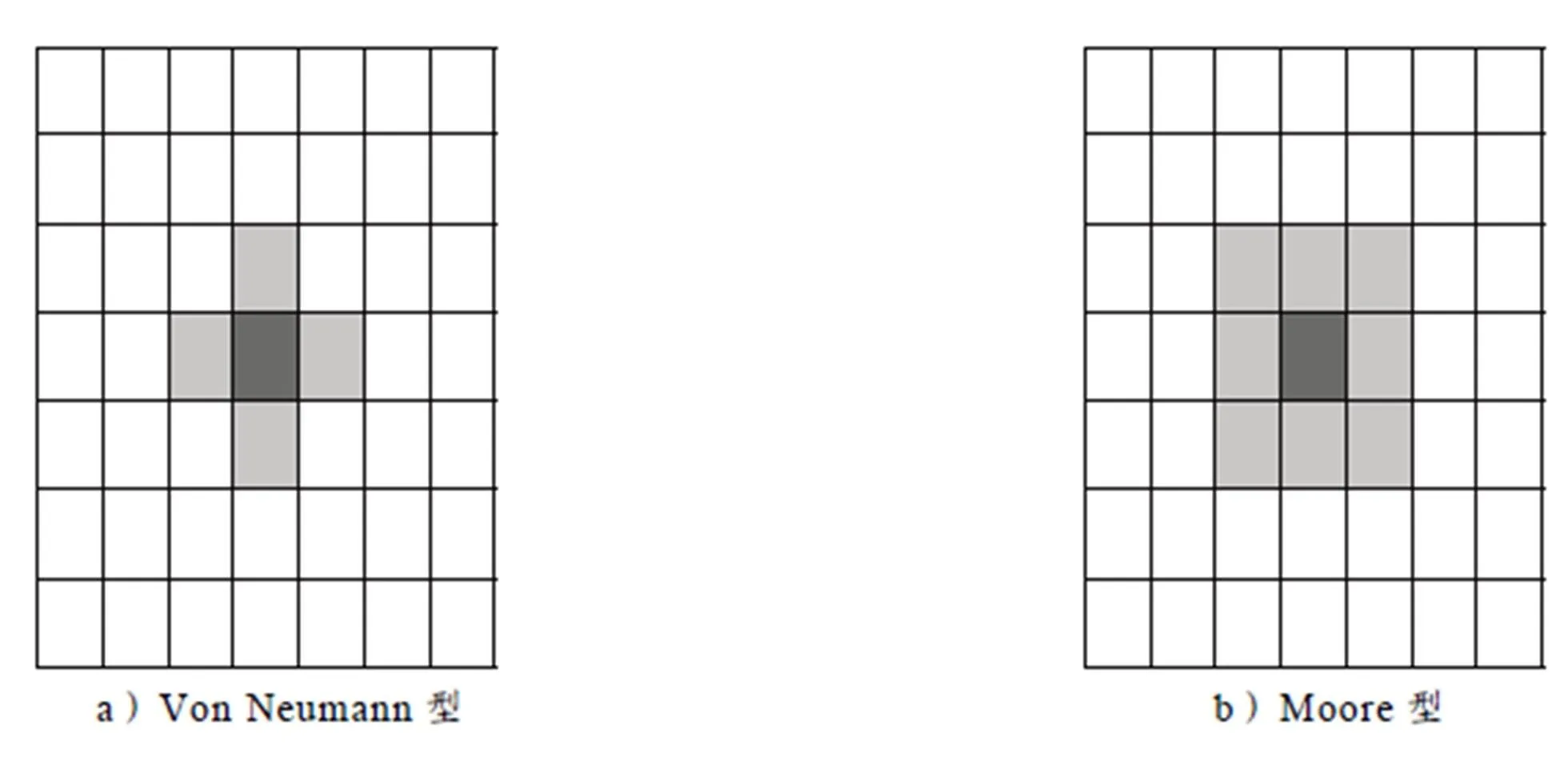
图1 元胞自动机的邻居模型

规则是元胞自动机演化的动力依据，是确定元胞下一时刻状态的动力学函数，即

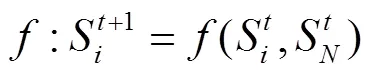
2 几种典型元胞自动机及其Matlab实现

在元胞自动机的发展过程中，科学家们构造了各种各样的元胞自动机模型. 以下几个典型模型对元胞自动机的理论方法的研究起到了极大的推动作用，因此，它们又被认为是元胞自动机发展历程中的几个里程碑.

2.1 初等元胞自动机

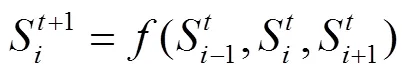
1: 111 110 101 100 011 010 001 000

+1: 000 010 000 000 010 010 000 000

: 010111110101011100010

+1: 1010001010101010001

每种组合分别对应0或1，共有组合28=256种，即初等元胞自动机只有256种不同规则. 根据上述8种组合产生的8个结果形成一个二进制（按照高低位顺序），如上述规则01001100，将其转化为十进制值：

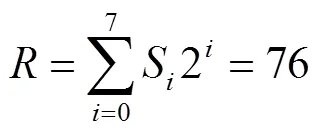
的取值范围为[0,255]，S.Wolfram定义该数值为初等元胞自动机的编号，于是前面的模型就是76号初等元胞自动机.

取长度为100的格子，每个格子代表一个元胞，初值取第50个格子为1，其余为0，用黑色表示0，白色表示1. 按照规则18和规则30演化100步，结果如图2和图3所示，Matlab实现见程序1和2.

图2 规则18的演化结果

图3 规则30 的演化结果

程序1

m=100;n=100;

s=zeros（m，n）;

s（1，n/2）=1;

for i=1：m-1

for j=2：n-1

if （s（i，j-1）==1&s（i，j）==0&s（i，j+1）==0）|（s（i，j-1）==0&s（i，j）==0&s（i，j+1）==1）

s（i+1，j）=1;

end

end

end

imagesc（s）;

colormap（gray）;

程序2

m=100;n=100;

s=zeros（m，n）;

s（1，n/2）=1;

for i=1：m-1

for j=2：n-1

if （s（i，j-1）==1&s（i，j）==0&s（i，j+1）==0）|（s（i，j-1）==0&s（i，j）==1&s（i，j+1）==1）|（s（i，j-1）==0&s（i，j）==1&s（i，j+1）==0）|（s（i，j-1）==0&s（i，j）==0&s（i，j+1）==1）

s（i+1，j）=1;

end

end

end

imagesc（s）

colormap（gray）

S.Wolfram对这256种不同规则的元胞自动机模型进行了深入而细致的研究[2]. 研究中发现，虽然初等元胞自动机的演化规则简单，但有些元胞自动机却能表现出非常复杂的空间形态. 有些元胞自动机经过一段时间的演化后，能形成一种稳定的状态，比如静止状态或周期性结构状态. S.Wolfram对初等元胞自动机的深入研究奠定了元胞自动机理论的基石，对后来兴起的人工生命研究和复杂性科学研究作出了巨大的贡献.

2.2 生命游戏

生命游戏是一种单人玩的计算机游戏，是J. H. Conway在20世纪60年代末设计的，它也是一种元胞自动机模型. 生命游戏中的元胞有{ “生”,“死” }两个状态，元胞类似国际象棋分布在网格内，根据元胞的局部空间形态来决定元胞下一时刻的生死. 生命游戏的构成及运算规则如下：

1）元胞位于规则划分的网格上；

2）元胞具有“生”和“死”两种状态，“死”用0代表，“生”用1代表；

3）元胞的邻居采用Moore型，即以相邻的8个元胞为邻居.

4）一个元胞下一时刻的状态由其在该时刻自身的生死状态和8个邻居的状态决定. 当前时刻，如果一个元胞状态为“生”，并且其8个邻居元胞中有2个或3个的状态为“生”，则在下一时刻该元胞为“生”，否则状态为“死”；当前时刻，如果一个元胞状态为“死”，并且其8个邻居元胞中恰好有3个元胞为“生”，则该元胞在下一时刻的状态为“生”，否则状态为“死”.

尽管这些规则看上去简单，但生命游戏经过一定时间的演化却能产生丰富有趣的图案. 生命游戏的演化与元胞的初始状态值有关. 任意给定初始状态，经过一定时间的演化，有的图案会消失，有的图案会稳定不变，也有的图案会重复多次出现.

生命游戏模型虽然简单，但却在许多方面得到应用，其演化规则接近生物群体的生存繁殖规律：在生命密度很小，即为“生”的邻居元胞数小于2时，因为孤独并缺乏互助、缺乏配种繁殖机会等，往往会出现生命危机，元胞的状态由生变为死；在生命密度很大，即为“生”的邻居元胞数大于3时，因为资源短缺、环境恶劣以及互相竞争而导致出现生存危机，元胞状态值由生变为死；只有处于个体数量适中，即为“生”的邻居元胞数为2或3时，生物才能保持良好的生存环境，才能保持元胞的状态值继续为生，并且繁衍后代，即元胞的状态值由死变为生. 因为该模型能够模拟生命活动中的生存、竞争、灭绝等复杂生物现象，因而得名为“生命游戏”.

生命游戏模型将平面划分成类似围棋的方格棋盘，每个方格称为一个元胞. 元胞的状态有2种：0代表死亡，1代表生存. 领域半径为1，邻居类型为Moore型，演化规则：

取一个初始状态，如图4所示，其中白色表示1（生），黑色表示0（死），根据演化规则，经过若干步达到一个稳定的状态，结果如图5所示，Matlab实现见程序3.

图4 初始状态

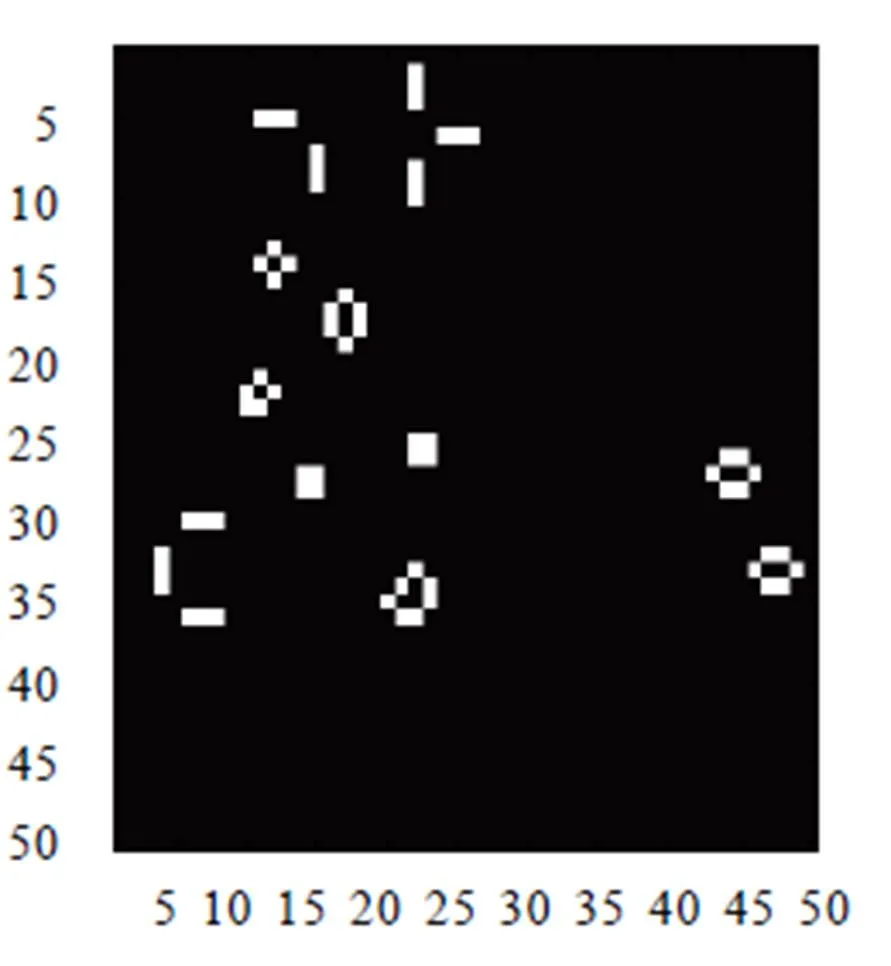
图5 演化后的稳定状态

程序3

n=50;

z = zeros（n，n）;

sum=z;

cells = z;

cells（n/2，.25*n：.75*n） = 1;

cells（.25*n：.75*n，n/2） = 1;

cells = （rand（n，n））<.5 ;

x = 2：n-1;

y = 2：n-1;

imagesc（cells）;

colormap（gray）

figure;

for i=1：500

sum（x，y） = cells（x，y-1） + cells（x，y+1） + ...

cells（x-1，y） + cells（x+1，y） + ...

cells（x-1，y-1） + cells（x-1，y+1） + ...

cells（x+1，y-1） + cells（x+1，y+1）;

cells = （sum==3） | （sum==2 & cells）;

imagesc（cells）

colormap（gray）

drawnow

end

3 元胞自动机的应用

元胞自动机已广泛应用于社会、经济、金融研究等各个领域. 元胞自动机在流体力学与统计物理中的应用代表是格子气自动机[3]，也称为格气机，它利用元胞自动机的动态特征来模拟流体粒子的运动. 在物理学中，除了格气机在流体力学上的成功应用，元胞自动机还应用于热扩散、热传导和机械波的模拟等. 另外，元胞自动机可以用来模拟二元规则共晶生长[4-5]，共晶生长是凝聚态物理和材料科学领域的重要研究课题.

元胞自动机在交通系统建模[6-8]中，主要研究类型和驾驶行为相同的车辆所构成的交通流问题，为解决城市交通问题提供一定的理论支持. 元胞自动机也是模拟复杂地理系统的有效工具[9-16]，广泛用于城市扩展和土地、森林资源利用变化的模拟.

在医学中，元胞自动机可以模拟病毒的传播和感染过程[17-18]，为疾病的控制和预防提供一定的帮助. 在化学中，元胞自动机可用来模拟原子、分子等各种微观粒子在化学反应中的相互作用，从而研究化学反应的过程[19]. 元胞自动机也可用于模拟人员疏散过程[20-23].

在金融投资分析中，元胞自动机可以模拟股票市场的行为. 文献[24-27]将元胞自动机的思想应用于金融市场的波动分析，元胞代表股票投资者，元胞的状态空间有3种：股票买入（-1）、股票持有（0）、股票买出（1），元胞下一时刻的状态受到邻居元胞的投资行为影响，这样可以根据自身元胞的从众心理定义元胞状态的形成规则，从而揭示金融市场中的从众效应和信息传递的动力学特征.

元胞自动机作为一种动态模型，其应用几乎涉及社会科学和自然科学的各个领域. 但目前大多数应用还仅局限在模拟仿真上，要达到真正的实用阶段还需深入研究.

[1] 吴今培，李学伟. 系统科学发展概论[M]. 北京：清华大学出版社，2010.

[2] WOLFRAM S. A new kind of science[M]. Champaign Illinois: Wolfram Media, 2002.

[3] 李元香，康立山，陈硫屏. 格子气自动机[M]. 北京：清华大学出版社，1994.

[4] 吴孟武，熊守美. 采用元胞自动机法模拟二元规则共晶生长[J]. 物理学报，2011, 60(5): 1-9.

[5] 武磊，刘雅政，程晓杰，等. 元胞自动机模拟晶粒长大的步长设定对模拟结果的影响[J]. 北京科技大学学报，2010, 32(6): 739-743.

[6] 贾斌. 基于元胞自动机的交通系统建模与模拟[M]. 北京：科学出版社，2007.

[7] 杜小丹，赵仕波，鄢涛，等. 基于自主代理和元胞自动机的交通流模型[J]. 计算机科学，2010, 37(5): 231-239.

[8] 雷丽，薛郁，戴世强. 交通流的一维元胞自动机敏感驾驶模型[J]. 物理学报，2003, 52(9): 2121-2126.

[9] 冯永玖，童小华，刘妙龙，等. 基于GIS的地理元胞自动机模拟框架及其应用[J]. 地理与地理信息科学，2010, 26(1): 41-43.

[10] 乔纪纲，何晋强. 基于分区域的元胞自动机及城市扩张模拟[J]. 地理与地理信息科学，2009, 25(3): 67-70.

[11] 王璐，岑豫皖，李锐，等. 基于区块特征的元胞自动机土地利用演化模型研究[J]. 地理与地理信息科学，2009, 25(3): 74-76.

[12] 尹长林，张鸿辉，刘勤志. 城市规划CA模型及其应用[J]. 地理与地理信息科学，2008, 24(3): 71-74.

[13] 全泉，田光进，沙默泉. 基于多智能体与元胞自动机的上海城市扩展动态模拟[J]. 生态学报，2011, 31(10): 2875-2887.

[14] 何春阳，史培军，陈晋，等. 基于系统动力学模型和元胞自动机模型的土地利用情景模型研究[J]. 中国科学：D辑，地球科学，2005, 35(5): 464-473.

[15] 王晓学，李叙勇，莫菲，等. 基于元胞自动机的森林水源涵养量模型新方法：概念与理论框架[J]. 生态学报，2010, 30(20): 5491-5500.

[16] 杨青生. 基于元胞自动机的土地资源节约利用模拟[J]. 自然资源学报，2009, 24(5): 753-761.

[17] 贺明峰，邓成瑞. 基于元胞自动机的SARS传播模型[J]. 数学的实践与认识，2008, 38(3): 41-46.

[18] 李璐，宣慧玉，高宝俊. 基于元胞自动机的异质个体HIV/AIDS传播模型[J]. 系统管理学报，2008, 17(6)：704-710.

[19] 李才伟. 元胞自动机及复杂系统的时空演化模拟[D]．武汉：华中科技大学，1997.

[20] 孟俊仙，周淑秋，饶敏. 基于元胞自动机的人员疏散仿真研究[J]. 计算机工程与设计，2009, 30(1): 241-246.

[21] 宋卫国，于彦飞，范维澄，等. 一种考虑摩擦与排斥的人员疏散元胞自动机模型[J]. 中国科学：E辑，2005, 35(7): 725-736.

[22] 翁文国，袁宏永，范维澄. 一种基于移动机器人行为的人员疏散的元胞自动机模型[J]. 科学通报，2006, 51(23): 2818-2822.

[23] 杨立中，方伟峰，黄锐，等. 基于元胞自动机的火灾中人员逃生的模型[J]. 科学通报，2002, 47(12): 896-901.

[24] 高建喜，刘源远，崔珊珊，等. 基于元胞自动机的股市模拟及分析：投资者心理和股票交易量[J]. 数学的实践与认识，2009, 39(4): 6-12.

[25] 应尚军，范英，魏一鸣. 单支股票市场的元胞自动机模型及其动力学研究[J]. 系统工程，2006, 24(7): 31-36.

[26] 应尚军，魏一鸣，范英，等. 基于元胞自动机的股票市场投资行为模拟[J]. 系统工程学报，2001, 16(5): 382-388.

[27] 刘源远，董宏光，高建喜，等. 基于元胞自动机的投资者心理与股价波动分析[J]. 科技通报，2008, 24(3): 427-432.

Developments of the Study of the Cellular Automata

SUNDe-shan

(Department of Math, Liaoning Normal University, Liaoning 116029, China)

Cellular automata are simple models of computation which exhibit complex behavior. They have captured the attention of many researchers, leading to an extensive research. The present paper deals with the advances of cellular automata and some of their applications in different fields.

cellular automata; cellular spaces; complex systems

1006-7302（2011）04-0022-07

N941.1

A

2011-07-20

孙德山（1970—），男，辽宁沈阳人，副教授，博士，研究方向为统计学习理论、机器学习方法.