一种新的元胞网络模型

李学伟，孙有发，吴今培

一种新的元胞网络模型

李学伟1，孙有发2，吴今培3

（1. 大连交通大学，辽宁 大连 116028；2. 广东工业大学 管理学院，广东 广州 510520；3. 五邑大学 智能技术与系统研究所，广东 江门 529020）

用元胞替换传统人工神经网络中的神经元，以局部连接取代相邻层级元胞之间的全连接，用规则演化算法替代BP算法，建立元胞网络模型. 设计了元胞网络的训练过程：内嵌的遗传算法用于寻优各元胞状态离散化边界值以及元胞网络拓扑结构. 以一个红酒分类基准数据为例，检验了元胞网络的学习性能和分类性能，获得了较为满意的结果.

元胞自动机；神经网络；遗传算法；规则演化；元胞网络

元胞自动机（Cellular Automata，CA）是定义在一个由具有离散、有限状态的元胞组成的元胞空间上，并按照一定局部规则，在离散的时间维上演化的动力学系统. 元胞自动机不是由严格定义的物理方程或函数确定，而是用一系列模型构造的规则构成[1-3].

神经网络（Neural Network，NN）是一类知识表达体系，通过对训练样本的学习，将专家知识以权值和阈值的形式存储在网络中，并利用网络中的信息完成不精确诊断推理，能较好地模拟专家凭经验、直觉的推理过程[4-6].

本文将元胞自动机与神经网络融合在一起，用元胞替换传统人工神经网络中的神经元，以局部连接取代相邻层级元胞之间的全连接，用规则演化算法替代BP算法，首次提出并建立元胞网络（Cellular Network，NN）模型. 由于元胞网络是基于规则的计算，与其他一些基于解析计算的智能技术相比，元胞网络将更擅长于解决现实世界中具有不稳定、非线性、不确定性、非结构化以及病态结构的复杂决策问题，为人们认识和模拟自然界的复杂现象提供了一种新的方法和工具.

本文提出的元胞网络概念，不同于著名文献[7-8]中的Cellular Neural Network（CNN，元胞或细胞神经网络），后者是一种局部互联的神经元电路设计，每个神经元有输入、输出以及有限种状态. 也不同于文献[9-11]中提到的Cellular Automata Neural Network（CA-ANN，元胞自动机－神经网络）或者基于神经网络的元胞自动机等概念，在该类文献中，神经网络是用来为元胞自动机获取规则的.

除此之外，在计算模式上，元胞网络与神经网络也有较大差异. 神经网络对知识的表示和利用，是把一切问题的特征都变为数字，然后通过设定的神经元函数，把一切推理都变为数值计算，即神经网络实质是一个解析函数[4-6]；而元胞网络以规则形式来表达隐含于训练样本中的分类知识，并直接利用规则推理出新任务的分类情况，是规则运算[1-3].

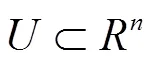
最后，元胞网络避免了神经网络结构识别产生的问题. 众所周知，神经网络的结构设计，迄今尚无系统的理论或原则可循，大多靠主观经验判断，或采用实验方法[4-6]；因而神经网络的结构识别问题，也是影响其泛化能力的主要因素和重要原因. 本文构建的元胞网络，应用遗传算法[14-15]寻优网络的拓扑结构，对复杂现象的结构识别问题进行了有益的探索.

1 元胞网络

1.1 输入层

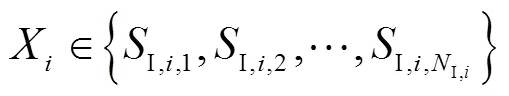
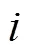
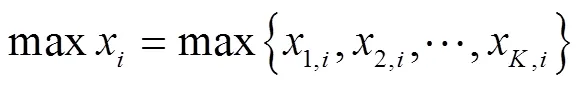
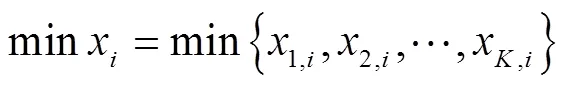
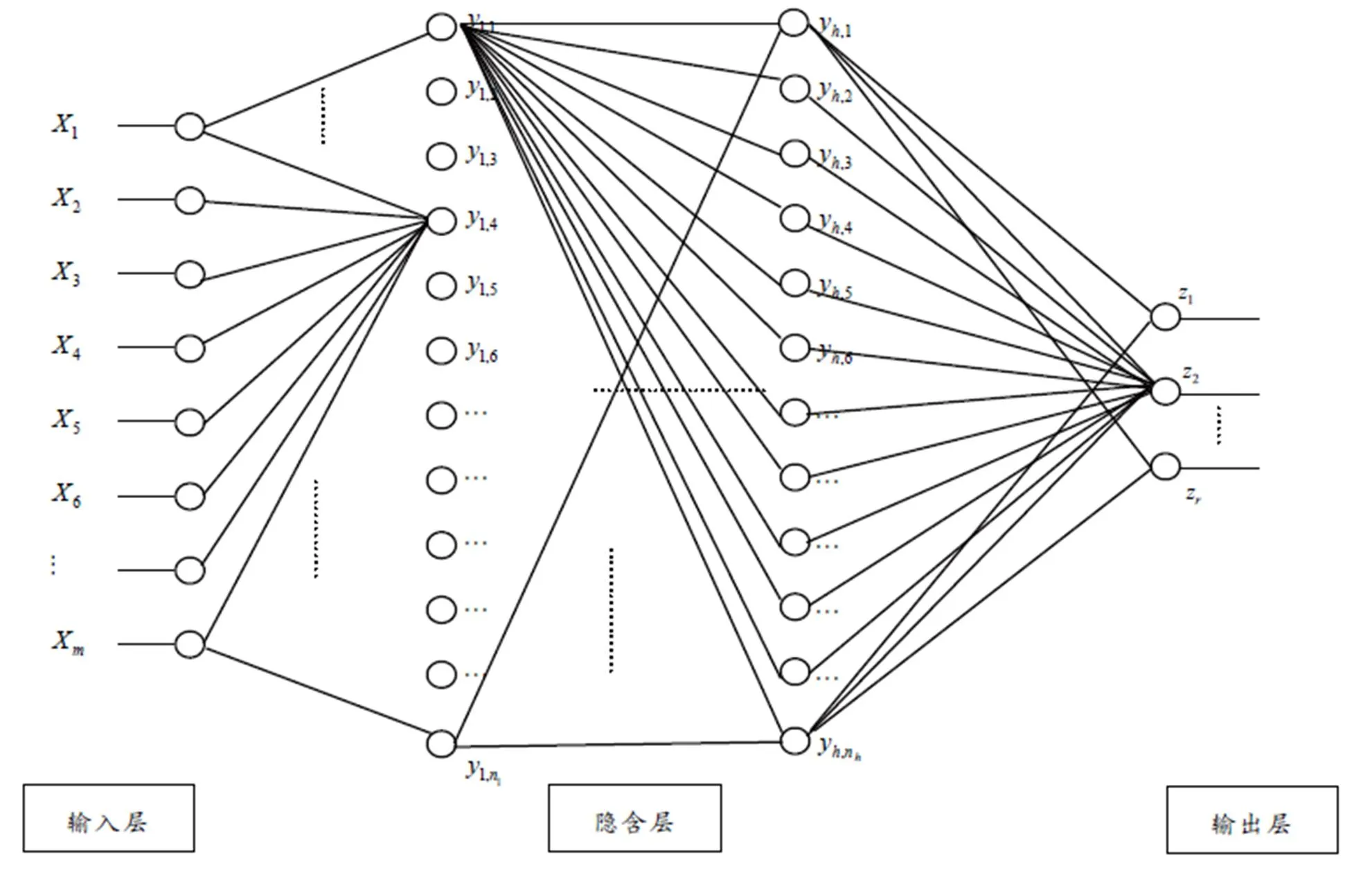
图1 元胞网络结构

1.2 隐含层

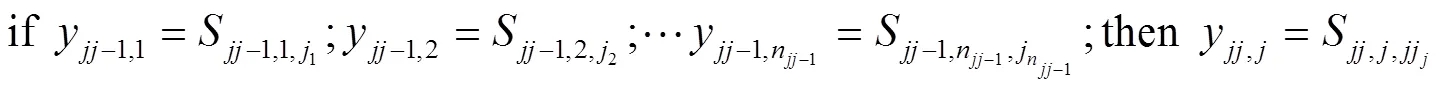
首先计算映射值

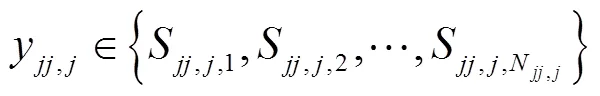
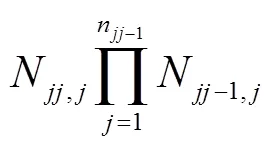
分段离散化方法中的边界值由遗传算法逐步寻优得到.

1.3 输出层

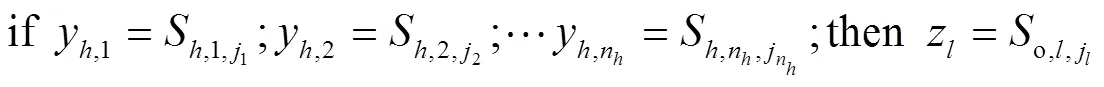
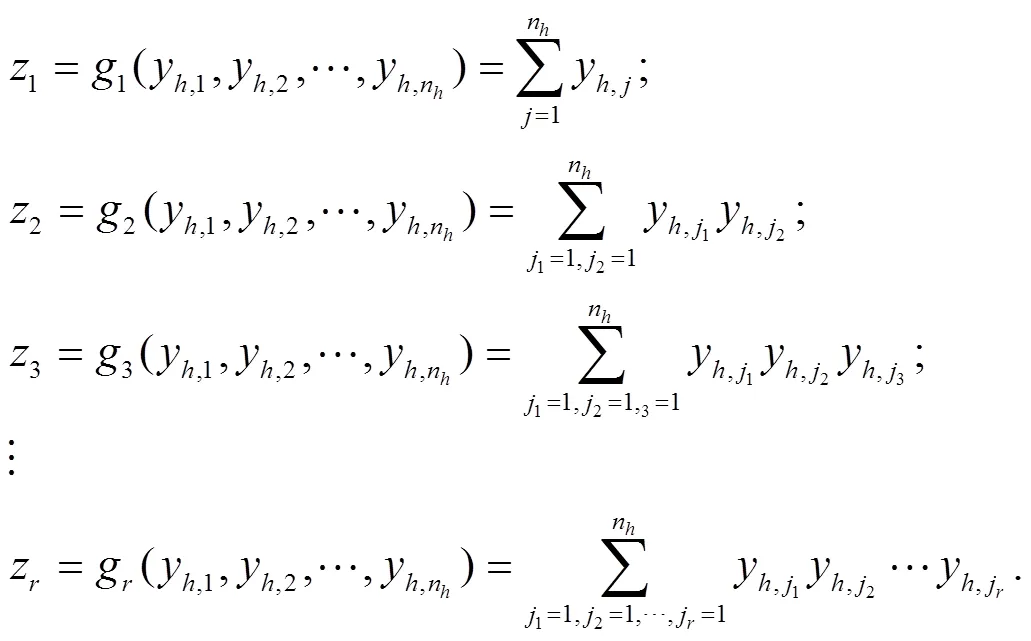
2 元胞网络的训练和预测过程

2.1 训练过程

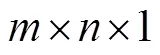
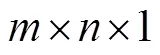
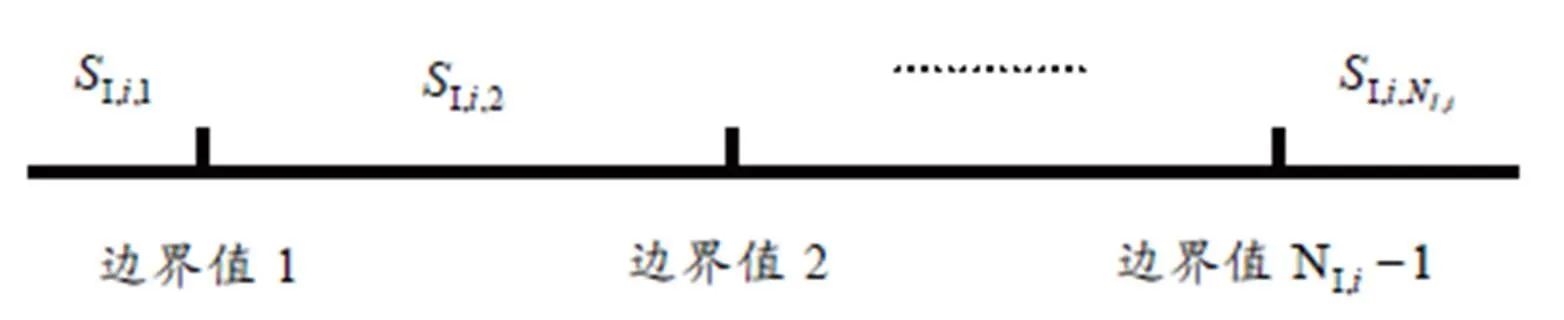
图2 元胞状态数与边界值的关系

元胞网络的训练过程包括如下5个步骤.

Step1 初始化元胞网络连接. 根据预先设定的各元胞状态数、样本各指标的输入区间以及各元胞的投影算法等，初始化全体元胞状态离散规则中的边界值.

Step2 将全体训练样本输入元胞网络，各元胞执行预先设定的投影算法和分段离散化规则，输出相应离散状态值，并最终确定元胞网络的输出，见图3. 具体过程分解如下：

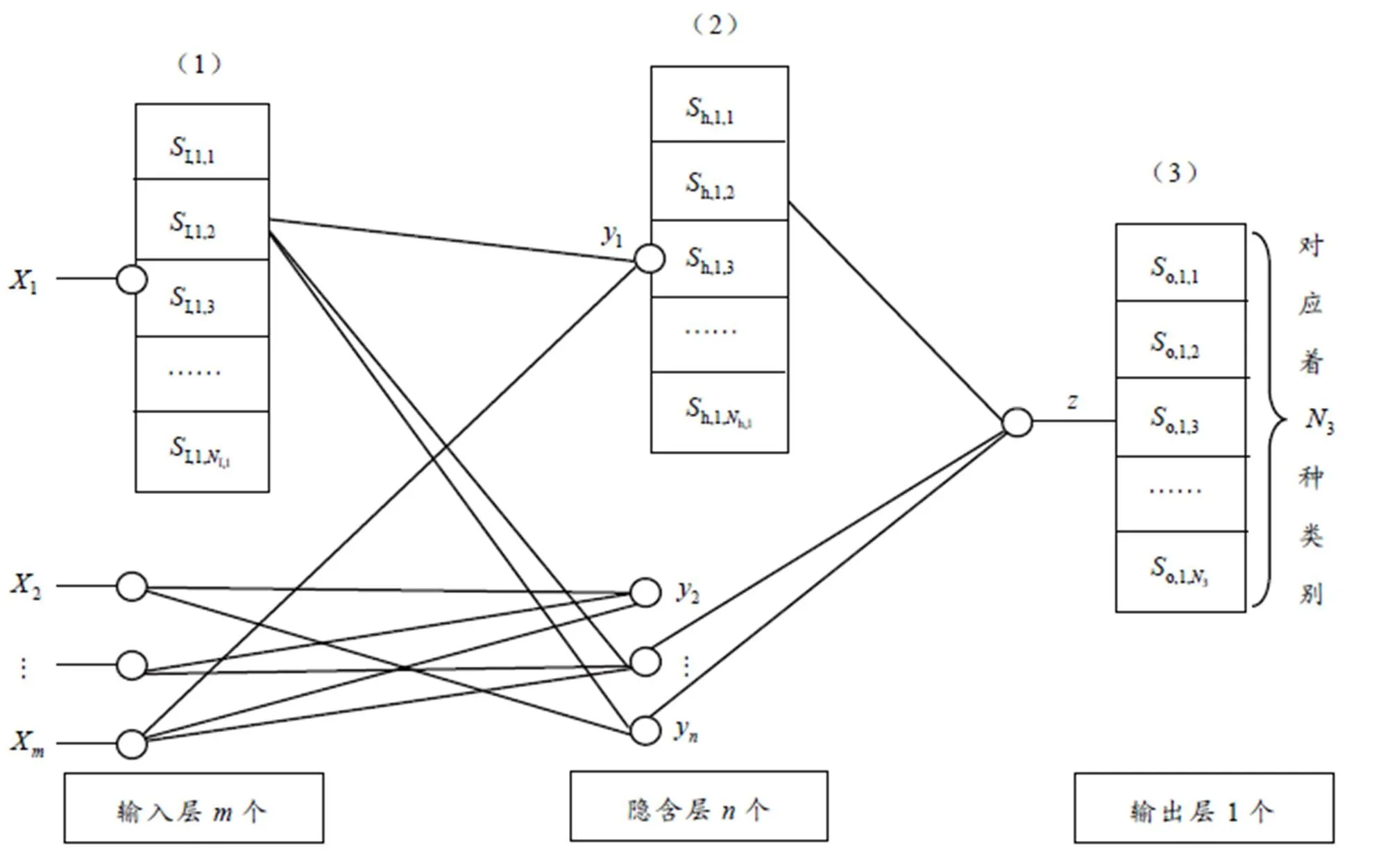
图3 元胞状态离散化

1）输入层各元胞执行状态离散化规则，从而原始样本的指标数据被离散化；

2）离散化后的样本指标输入到隐含层，隐含层各元胞执行投影算法和分段离散化规则，得到隐含层的离散化输出；

3）隐含层的输出输入到元胞网络的最后一层，输出层元胞执行投影算法和分段离散化规则，得到元胞网络的最终输出（即某种分类状态）.

Step3 计算该次分类状态的准确度.

Step5 达到设定的最大演化代数或者其他演化停止条件，元胞网络训练结束，输出“优化规则”网络.

2.2 预测过程

元胞网络经过训练后，确定了网络优化连接状态以及分段离散化规则所需要的各个边界值，此时，训练后的元胞网络实质上已成“规则网络”，具备了模式识别功能，可以用来预测新样本的分类情况等.

预测操作很简单，只需将新样本的指标值输入到元胞网络，输出的状态值即是元胞网络建议该样本的分类类别.

3 应用

3.1 基准数据描述

本文采用的意大利红酒基准分类实验数据①来自加利福尼亚大学尔湾分校（University of California，Irvine，UC Irvine）国际机器学习论坛，该数据是对出产于意大利同一地区的3个不同品种葡萄酒的化学成分分析，包含13个成分数据，它们分别是：1）Alcohol；2）Malic acid；3）Ash；4）Alcalinity of ash；5）Magnesium；6）Total phenols；7）Flavanoids；8）Nonflavanoid phenols；9）Proanthocyanins；10）Color intensity；11）Hue；12）OD280/OD315 of diluted wines；13）Proline. 该基准分类数据共有178例样本，分3类.

根据国际机器学习统计，意大利红酒分类基准数据被点击过93 348次，引用此基准分类数据的国际知名文献有40多篇，其中文献[16-17]获得了较为理想的分类结果：通过规则化识别分析（RDA）获得了100%的分类精度，采用二次识别分析（QDA）方法取得99.4%的分类精度，采用线性识别分析（LDA）方法获得98.9%的分类精度，采用人工神经网络技术获得的分类精度为96.1%. 这些分类方法均采用的是留一法（leave-one-out）.

本文应用元胞网络于上述红酒分类基准实例，目的是检验元胞网络的学习能力和预测性能等. 与上述“留一法”不同的是，本文采取对半分基准数据方法：一半用于训练，另一半用于预测. 从理论上讲，本文采用的“对半分”方法的分类程度要大于留一法.

3.2 元胞网络的初始拓扑结构设计

3.3 训练

设定遗传算法总群规模为50，演化代数为100次，交叉概率为0.8，变异概率为0.10，图4是执行遗传算法1次的演化过程图. 本次元胞网络训练后输出的边界值见表3，网络连接状态的优化过程见图4a）.

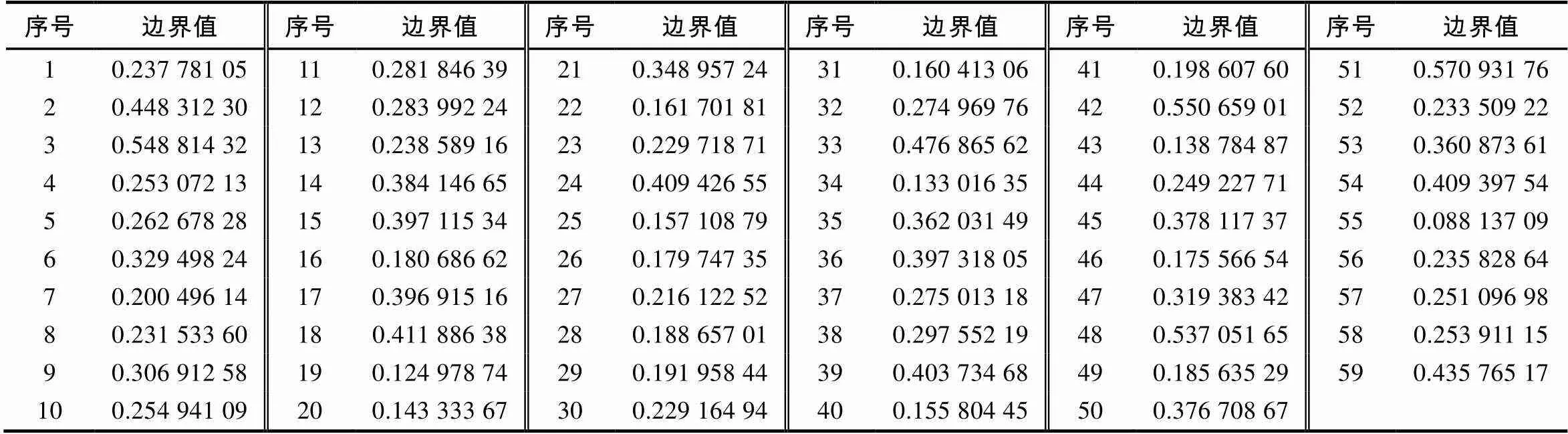
表3 元胞网络训练结束后输出的优化边界值

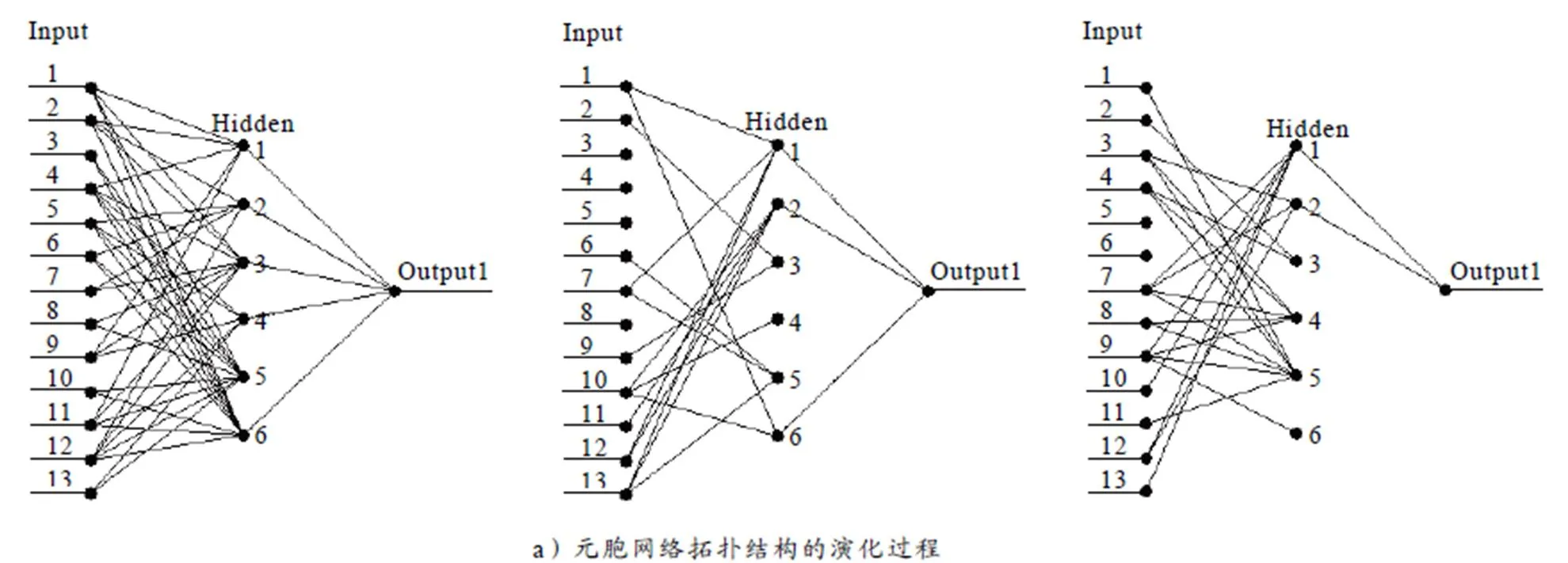
图4a）显示，随着演化的进展，整个元胞网络的连接状态在不断调整；群体的平均适应值以及群体中最佳个体的适应值也逐步得到提升，见图4b）. 这充分展示了演化算法的优良性能，也反应了本文元胞网络的学习性能.

3.4 预测

用图4所示的训练后的元胞网络对余下的一半样本进行分类测试，经检验，元胞网络的分类准确度为94.4%.

4 结论

本文首次提出元胞网络概念，并建立元胞网络模型，设计了训练过程，用遗传算法寻优元胞网络拓扑结构以及元胞状态离散化边界值. 应用于红酒分类国际基准实例，元胞网络取得了较满意的分类精确度.

[1] WOLFRAM S. Cellular automata as models of complexity[J]. Nature, 1984, 311(4): 419-424.

[2] WOLFRAM S. Theory and application of cellular automata[M]. Singapore: World Scientific, 1986.

[3] WOLFRAM S. A new kind of science[M]. Champaign Illinois: Wolfram Media, 2002.

[4] BISHOP C M. Neural networks for pattern recognition[M]. Oxford: Oxford University Press, 1996.

[5] MITCHELL T M. Machine learning[M]. New York: McGraw-Hill, 1997.

[6] RUMELHART D, WIDROW B, LEHR M. The basic ideas in neural networks[J]. Communications of the ACM, 1994, 37(3): 87-92.

[7] CHUA L O, YANG L. Cellular neural networks: theory[J]. IEEE Trans Circuits Syst, 1988a, 35(10): 1257-1272.

[8] CHUA L O, YANG L. Cellular neural networks: applications. IEEE Trans Circuits Syst, 1988b, 35(10): 1273-1290.

[9] LI Xia. YEH A G O. Neural-network-based cellular automata for simulating multiple land use changes using GIS[J]. International Journal of Geographical Information Science, 2002, 16(4): 323-343.

[10] YEH A G O, LI Xia. Integration of neural networks and cellular automata for urban planning[J]. Geo-Spatial Information Science, 2004, 7(1): 6-13.

[11] 徐昔保，杨桂山，张建明. 基于神经网络CA的兰州城市土地利用变化情景模拟[J]. 地理与地理信息科学，2008, 24(6): 80-84.

[12] HUANG S H, XING Hao. Extract intelligible and concise fuzzy rules from neural networks[J]. Fuzzy Sets and Systems, 2002, 132(2): 233-243.

[13] ZADEH L A. Fuzzy logic, neural networks, and soft computing[J]. Communications of the ACM, 1994, 37(3): 77-84.

[14] 孙有发，张成科，高京广，等. 带反馈的混沌并行GA及其在非线性约束优化中的应用[J]. 计算机学报，2007, 30(3): 424-430.

[15] 孙有发，陈世权，吴今培. 一种非一致性的自适应遗传算法与应用[J]. 系统工程，2002, 20(62): 82-86.

[16] AEBERHARD S, COOMANS D, VEL O de. Comparison of classifiers in high dimensional settings, Tech Rep no 92-02, 1992, Dept of Computer Science and Dept of Mathematics and Statistics, James Cook University of North Queensland.

[17] AEBERHARD S, COOMANS D, VEL O de. The classification performance of RDA. Tech Rep no 92-01, 1992, Dept of Computer Science and Dept of Mathematics and Statistics, James Cook University of North Queensland.

① http://archive.ics.uci.edu/ml/datasets/Wine.

A New Kind of Cellular Network

LIXue-wei1, SUNYou-fa2, WUJin-pei3

(1. Dalian Jiaotong University, Dalian 116028, China; 2. School of Management, Guangdong University of Technology, Guangzhou 510520, China; 3. Institute of Intelligence Technology and Systems, Wuyi University, Jiangmen 529020, China)

A novel concept of cellular network is proposed. The cellular network is constructed based on the traditional artificial neural network by replacing the neurons with cells, replacing the full connections among cells with partial connections, and replacing the back-propagation algorithm with rule-evolution algorithm. The training process of cellular network is also designed. The embedded genetic algorithm is to search for the optimal parameters and structures of the network. Finally, the cellular network is applied to a benchmark data set (classification of Italy’s red wine), and is validated to be of good performances of learning and predicting.

cellular automata; neural network; genetic algorithm; rule evolution; cellular network

1006-7302（2011）04-0014-08

TP393.01

A

2011-07-20

国家自然科学基金资助项目（No.70571006；No.70801019）

李学伟（1962—），男，河南宜阳人，教授，博士，博士生导师，研究方向为管理科学与复杂系统决策理论方法等.