自适应元胞遗传算法与股票价格行为分析

李雪岩，孙有发，刘彩燕



自适应元胞遗传算法与股票价格行为分析

李雪岩，孙有发，刘彩燕

（广东工业大学 管理学院，广东 广州 510520）

与以往侧重于刻画从众模仿行为的元胞自动机价格模型不同，论文基于Moore型邻居投资者分布结构，以预测精度为切入点，将遗传算法引入到元胞自动机股票价格模型中，投资者与“邻居”沟通和分享信息，并由遗传算子来优化其对股价进行预测的各要素权重；研究了两种预测模式下的权重演化行为，以及权重交叉概率对股价行为（收敛性、波动性等）的影响；模拟了预期驱动下，股价与市场情绪的关系. 研究认为：元胞遗传算法的引入，较好地驱动着股票价格回归基本价值，减轻了股票市场的波动性.

遗传算法；自适应元胞自动机；股票市场；股价

作为典型的复杂自适应系统，股票市场价格演化过程是由诸多经济个体及宏微观因素共同参与决定的. 系统内部个体的自组织、自加强、自协调[1]等行为使股票价格变化具有极大的不确定性，经典的有效市场理论、传统的数学工具和当前的资产定价模型已无法解释金融市场的复杂现象.

1951年，Von Neumann提出了元胞自动机. 该方法具有并行、局部规则、齐次和离散等良好特性，能为股票市场复杂性的研究提供一条可行的途径. 国内学者应尚军等[2-4]率先建立了单只股票的元胞自动机演化模型并对模型进行了动力学分析，通过与现实市场的对比研究，验证了元胞自动机模型在模拟股票市场复杂性方面的可行性. 随后，学者们[5-8]又相继将元胞自动机模型运用于股票市场投资行为的刻画和分析中，并取得了丰富的研究成果.

然而，上述研究在利用元胞自动机描述投资者之间的信息交互时，侧重点往往放在“从众行为”或“模仿”上，投资者过分依赖“群体决策”而缺乏自主判断、智慧程度低. 于是，部分学者开始求助一些人工智能技术来构建金融市场投资者模型. 邹琳等[9]提出了—个新的人工金融市场模型，该模型利用遗传算法来刻画自适应主体Agent的学习规则进化，提高了投资者的智能化程度，但该模型忽视了投资者之间的交互行为. K Matsumoto[10]将遗传算法引入自适应主体Agent的价格预测交互学习行为中并产生了理想的预测精度. 另一类文献从纯算法设计的角度出发，探讨了将遗传算法引入元胞自动机模型的寻优效果变化. 万成等[11]分析了动态环境下元胞遗传算法的适应性能和精确性能，并用实验验证了元胞遗传算法比标准遗传算法具有更好的求解效果. 李莉等[12]使用元胞自动机的生命游戏规则替代遗传算法的交叉算子，提出一种多目标元胞遗传算法，并证明其具有良好的收敛性和稳定性. 张俞等[13]通过对“生命游戏”演化规则的改进，改善了元胞遗传算法求解复杂多峰函数优化问题的效果. 上述研究表明，将遗传算法的思想引入到元胞自动机模型具有可行性，并且这些基于不同演化规则的元胞遗传算法均体现出了良好的鲁棒性.

与以往侧重于从众模仿行为的元胞自动机价格模型不同，本文基于Moore型邻居投资者分布结构，以预测资产价格精度为切入点，将遗传算法引入元胞自动机股票价格模型，对投资者的价格预测因子权重系数进行寻优，投资者依据遗传算子更新权重系数、产生新的预测价格，并与邻居交互，寻求更高的预测精度. 为此，本文首先建立基于上述演化规则的元胞自动机股票价格模型；然后分析权重演化、信息权重交叉概率对价格序列的影响，价格收敛性与市场情绪的关系；最后，开展数值仿真实验，以验证理论分析结论.

1 模型

1.1 市场假设

1）以一只股票作为研究对象，忽略投资者财富状况、交易费用的限制.

2）交易机制为做市商定价.

3）投资者无硬性的类型区分，均为有限理性，均依据对股票价格的预测做出交易决策，但对各种预测方式的倾向程度（权重）不同.

4）投资者的价格预测模式中，各种可能要素包括：基本价值信念、短期移动平均、中期移动平均和长期移动平均（这里的短期、中期、长期是相对而言的）.

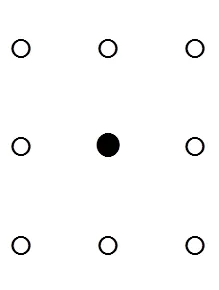
图1 元胞邻居形式

1.2 元胞自动机假设

2）邻居形式：与文献[4]相同，本文采用Moore型邻居，即每个元胞拥有8个邻居，如图1所示.

3）元胞自动机规则：每个元胞（投资者）依据不同的预测要素权重系数产生对价格的预测，决定需求，每次价格更新后，再以实际价格为基准，通过与邻居的沟通比较来调整自身的权重系数，以寻求更高的预测精度.

1.3 价格预测模式假设

依据前文假设，设计两种预测模式，模式1仅采用历史价格信息，模式2在模式1的基础上叠加股票基本价值信息，详见表1和表2.

表1 预测模式1

表2 预测模式2

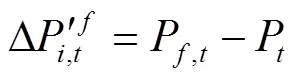
两种预测模式下的股价加权预期变化表达式如下：

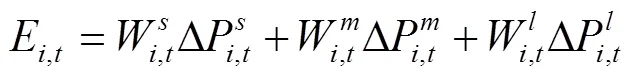
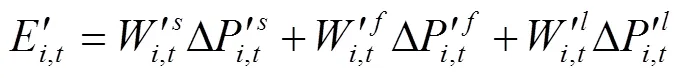
1.4 价格动力学方程

依据Carl Chiarella等[14-15]对技术分析者风险资产需求函数的定义以及其设计的资产定价模型框架，结合式（3～4），两种预测模式下投资者的需求函数及价格动力学方程分别定义如下：

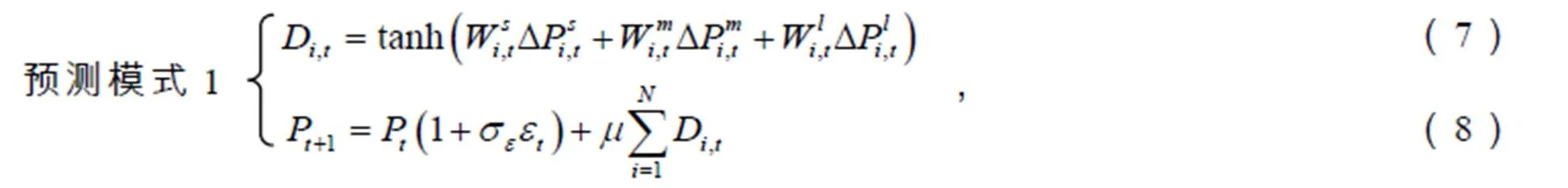
2 自适应元胞遗传算法演化规则

本文将遗传算法的思想引入元胞自动机演化模型，赋予投资者自适应与自学习的特点，具体表现为每位投资者依据不同的预测要素权重系数产生对价格的预测，决定需求，每次价格更新后，以实际价格为基准，通过与邻居的沟通比较来调整该权重系数，寻求更高的预测精度. 篇幅所限，本节仅以预测模式1为例，预测模式2权重演化规则与模式1相同，不详述.

2.1 适应度函数

定义两种预测模式的元胞价格预测精度评价函数

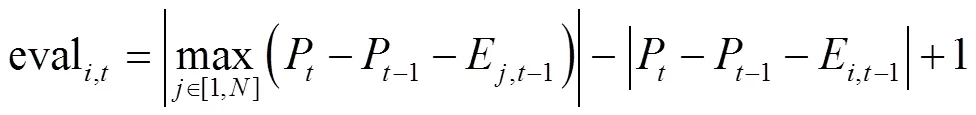
2.2 选择

2.3 交叉

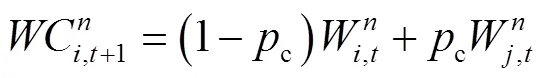
2.4 变异

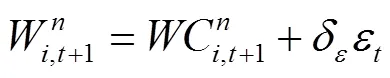
3 模型分析

3.1 模型均衡点

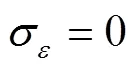
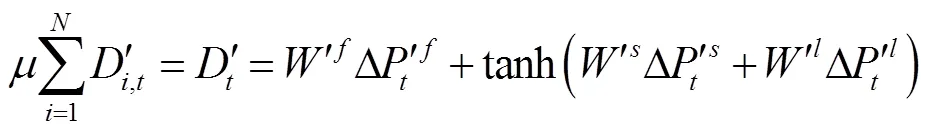
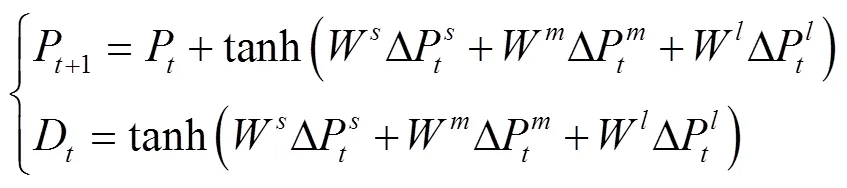
结合式（1～3），将式（17～18）进一步展开，可得如下常微分动力系统

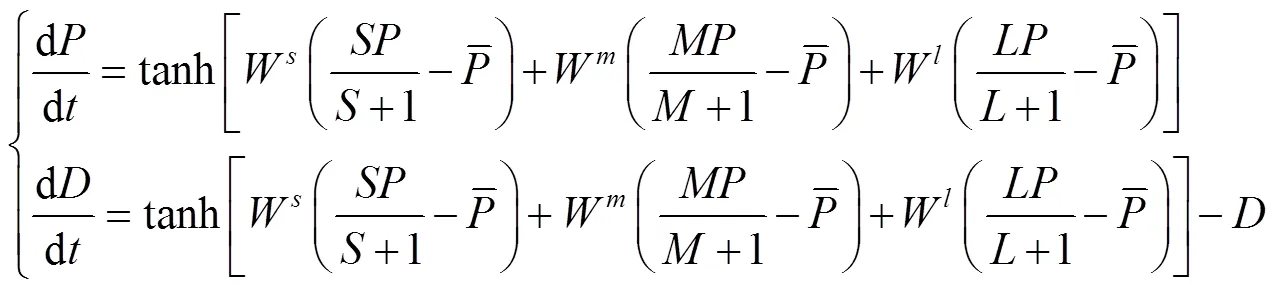
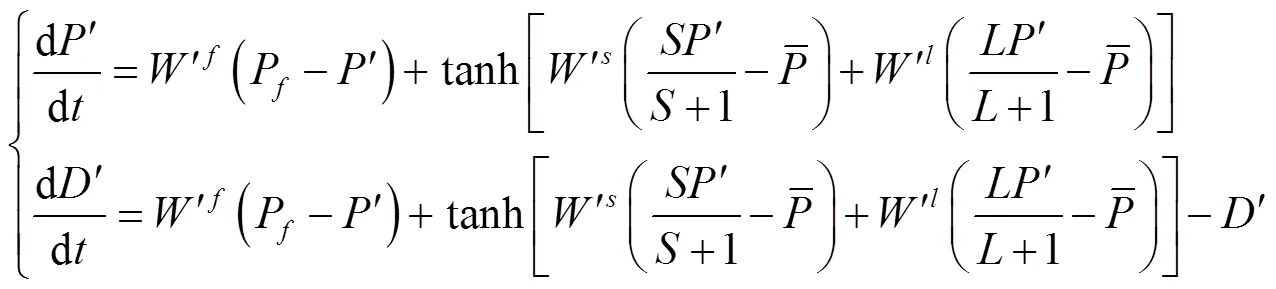
3.2 价格收敛性

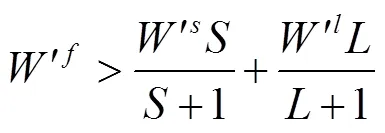
3.3 价格波动与市场情绪的异步性

以预测模式1为例，结合式（13）及式（15），得到价格演化方程

4 计算机仿真

4.1 仿真参数设定

仿真时，除特别指出，参数均按表3取值.

表3 仿真参数

4.2 预测权重演化

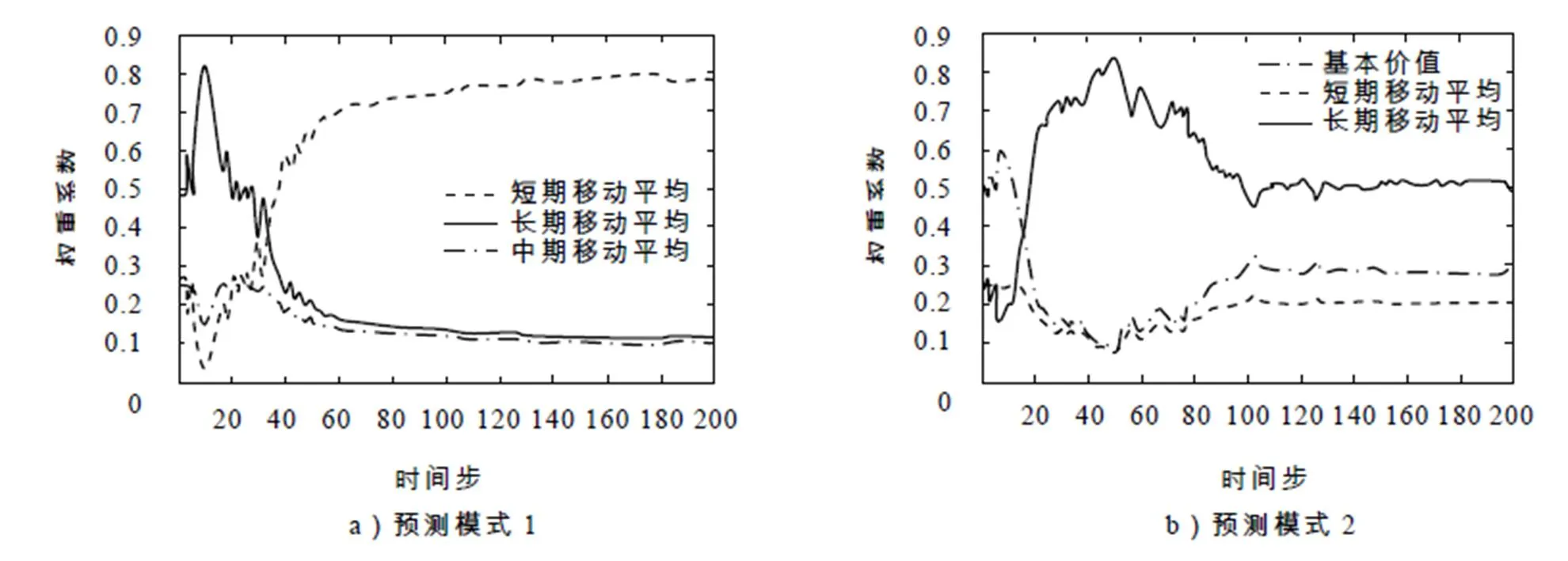
图2 预测要素权重演化

由图2及表4可以发现：当投资者仅依据移动平均技术手段进行价格预测（图2a））时，由于相对于中期和长期移动平均，短期移动平均对价格变化最为敏感，最能及时准确地反映价格变化，从而导致投资者对其倾向程度不断增大而造成价格波动异常；股票基本价值纳入预测参考要素后（图2b）），投资者逐渐形成了基本价值信念，其对基本价值的平均参考权重不断提高，从而驱动股票价格呈现基本价值收敛. 这一现象，与Carl Chiarella等[14-15]“稳态下，价格回归基本价值”的结论一致.

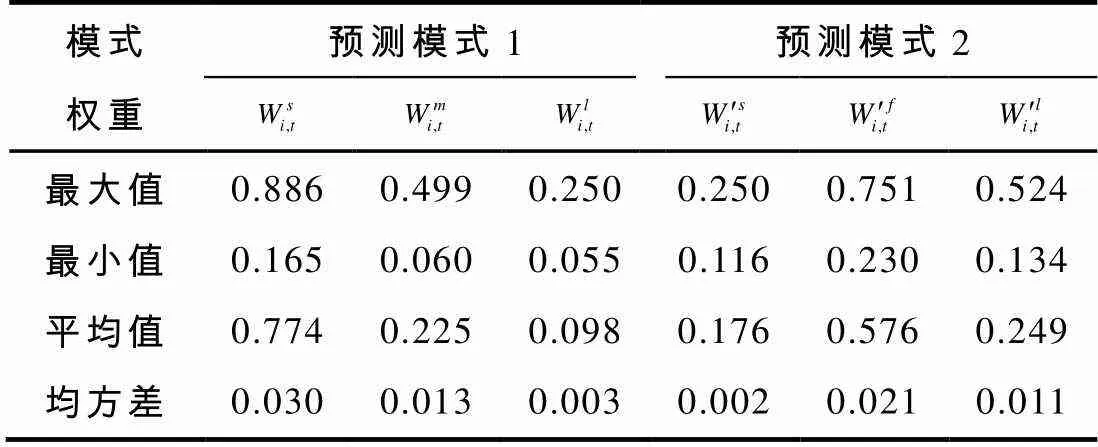
表4 权重演化结果（独立实验100次）

4.3 价格行为

4.3.1 预测模式1

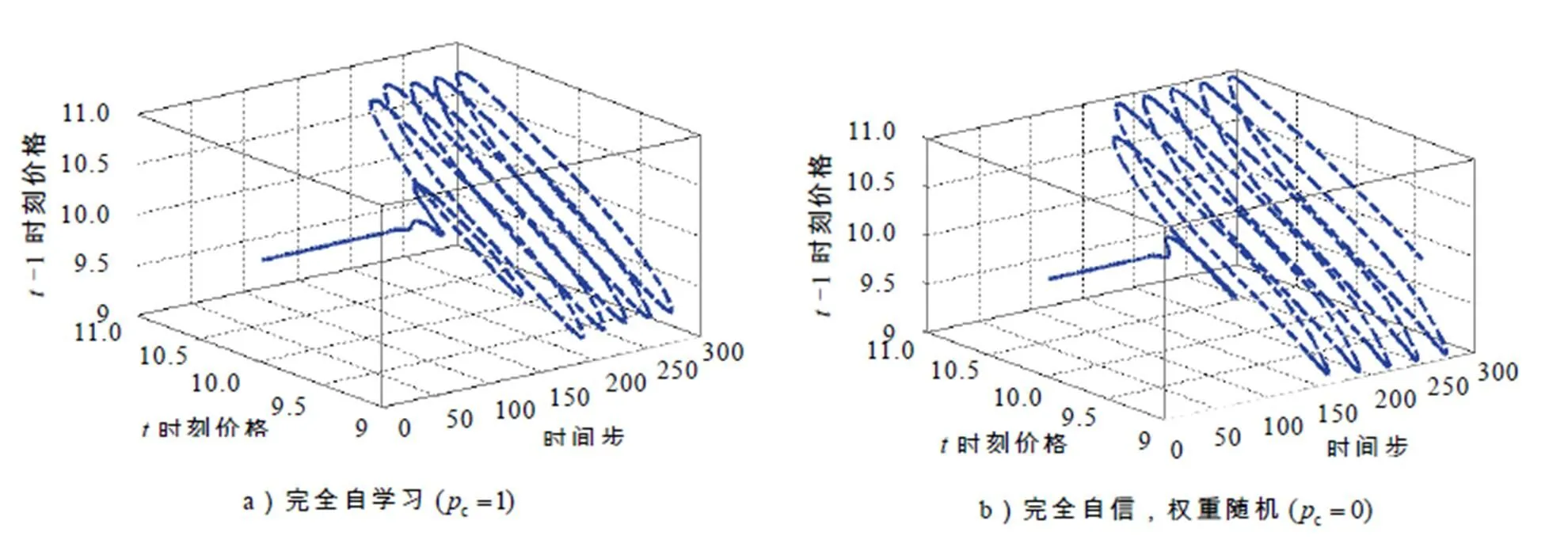
表5 交叉概率与价格偏离均值程度 （独立实验100次）

通过观察图3及表5不难发现：1）投资者仅依据移动平均技术手段预测价格时，股市震荡强烈，价格不收敛；2）引入具有自学习性质的元胞遗传算法后，价格震荡（波动）幅度减小，这说明自学习机制减少了投资行为中的非理性成分，仿真结果与前述理论分析一致；3）全体投资者订单总量之和代表了宏观市场情绪（订单总量为正，买方占优，反之亦然），市场情绪（订单总量）的极值点总是领先于价格极值点，市场情绪与价格的异步性体现了投资者的价格预测行为对实际价格的引导作用，仿真结果验证了3.3节的理论分析，体现了本模型“预期驱动”的特点.

4.3.2 预测模式2

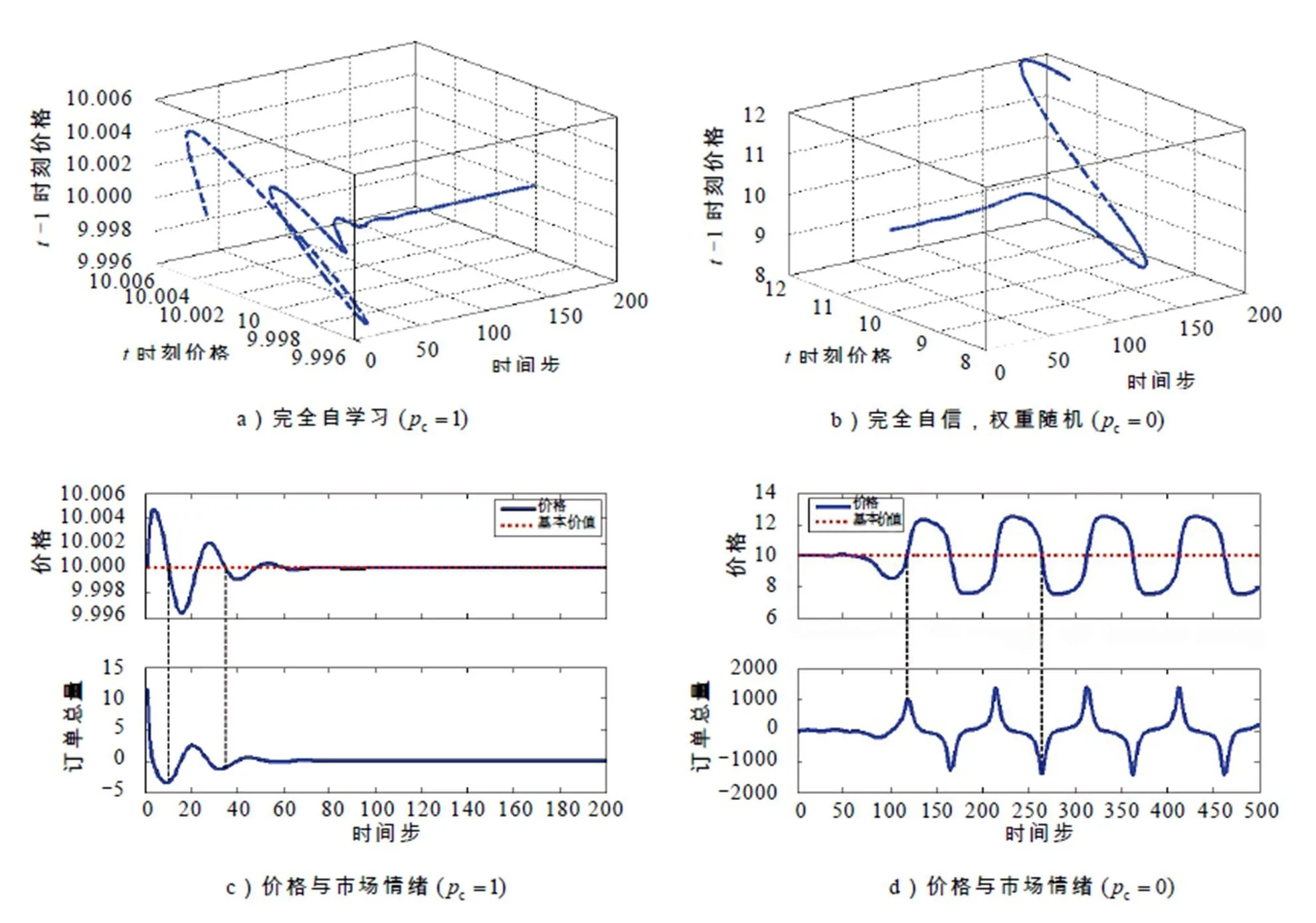
图4 预测模式2的价格演化

4.4 预测精度评价函数值

随机选择若干元胞，标记跟踪，记录每单位时间其价格预测精度评价函数值（均值），结果见图5.

观察图5可以发现，投资者的价格预测行为经过自适应遗传算法改进与优化后，预测精度评价函数值随时间变化呈现提高的趋势. 可见，投资者的智能化程度得到了提高.

图5 预测精度评价函数值

5 结论

本文以价格预测精度作为切入点，将遗传算法的思想引入元胞自动机价格模型的规则演化，建立了价格演化的动力模型，并进行理论分析及数值仿真. 与以往元胞自动机模型的研究注重“从众模仿”不同，本文对投资者个体的投资决策行为进行了自适应遗传算法改进与优化，提高了自适应主体的智能化程度和自学习能力. 研究认为：元胞遗传算法的引入，驱动股票价格呈现基本价值收敛，减小了价格波动性. 未来的研究包括：将更多的人工智能算法引入元胞自动机价格演化模型，对价格行为进行更为深入的对比及探讨.

[1] 袁毅贤，梁莹. 基于Agent计算金融的计算机仿真研究综述[J]. 计算机仿真，2007(2): 262-265.

[2] 应尚军，魏一鸣，范英，等. 基于元胞自动机的股票市场复杂性研究：投资者心理与市场行为[J]. 系统工程理论与实践，2003, 12: 18-24.

[3] 应尚军，范英，魏一鸣，等. 基于投资分析的股票市场演化元胞自动机模型[J]. 管理评论，2004, 11: 4-9.

[4] 应尚军，范英，魏一鸣. 单支股票市场的元胞自动机模型及其动力学研究[J]. 系统工程，2006, 7: 31-36.

[5] 吴军，李青. 基于元胞自动机的股票价格宏观变化的研究[J]. 计算机仿真，2009, 7: 298-301.

[6] 高建喜，董宏光，刘源远，等. 基于元胞自动机的股市模拟及分析：投资者心理和股票交易量[J]. 数学的实践与认识，2009, 2: 6-12.

[7] 黄宗远，沈小燕. 羊群行为的元胞自动机模拟分析[J]. 广西师范大学学报：哲学社会科学版，2009, 6: 43-48.

[8] 丁竞渊，李青，李桢. 预测传播结构与人工金融市场的易变性[J]. 复杂系统与复杂性科学，2009, 9: 50-56.

[9] 邹琳，马超群，李红权. 中国股市仿真系统建模及其非线性特征研究[J]. 系统管理学报，2008, 17(4):385-389.

[10] MATSUMOTO K. Evaluation of an artificial market approach for GHG emissions trading analysis[J].1 Simulation Modeling Practice and Theory, 2008, 16: 1312-1322.

[11] 万成，杨小芹，鲁宇明. 动态环境下的元胞遗传算法研究[J]. 电子元器件应用，2010, 7: 78-79.

[12] 李莉，常秉琨，卢青波. 多目标元胞遗传算法及其应用[J]. 现代制造工程，2010, 7: 46-50.

[13] 张俞，黎明，鲁宇明. 元胞遗传算法演化规则的研究[J]. 计算机应用研究，2009, 10: 3635-3638.

[14] ZHU Mei, CHIARELLA C, HE Xue zhong, et al. Does the market maker stabilize the market? [J]. Physica: A, 2009, 388: 3164-3180.

[15] CHIARELLA C, HE Xue zhong, HOMMES C. A dynamic analysis of moving average rules[J]. Journal of Economic Dynamics & Control, 2006, 30: 1729-1753.

The Adaptive Cellular Genetic Algorithm and an Analysis of Stock Prices

LIXue-yan, SUNYou-fa, LIUCai-yan

(School of Management, Guangdong University of Technology, Guangzhou 510520, China)

Different from the traditional cellular automata models of stock prices which always focus on imitating, this paper introduces genetic algorithm into cellular automata models of stock prices based on the Moore neighborhood and the point-cuts for price prediction, so that investors can communicate and share information with their neighbors and optimize the weights of factors in price prediction using algorithm operators. It also studies evolution of weights under two prediction modes and crossover probability’s impact on price (convergence, volatility), and simulates the connection between stock price and sentiment of market. The study shows that the introduction of cellular genetic algorithm can preferably drive stock price back to the fundamental price and reduce the volatility of the stock market.

genetic algorithm; adaptive cellular automata; stock markets; stock prices

1006-7302（2011）04-0057-09

F830.91

A

2011-07-20

国家自然科学基金资助项目（No.70801019）

李雪岩（1987—），男，内蒙古呼和浩特人，在读硕士生，研究方向为金融系统工程；孙有发，博士，副教授，硕士生导师，从事复杂系统建模与仿真、金融系统工程的研究.