发动机旋转整流帽罩的水滴撞击特性分析

赵秋月，董 威，朱剑鋆

(上海交通大学机械与动力工程学院，上海200240)

1 引言

飞机及发动机的防/除冰技术是现代飞机研制中的一项关键技术[1，2]。当飞机在结冰气象条件下以较低速度飞行时，空气中的过冷水滴容易在飞机及发动机进气系统的迎风面上发生冻结，从而破坏飞机及发动机的气动性能，危害飞行安全。对于航空发动机而言，迎风面结冰除了影响发动机进气性能外，若结冰发生脱落还会被吸入发动机内部并与高速旋转中的叶片发生碰撞，对发动机造成损伤。为此，必须在发动机设计时对其几何外形下的水滴撞击特性进行充分研究，并采取相应的防/除冰措施。

目前，世界上主流的发动机防冰系统主要有加热式和不加热式两种。前者从压气机中引出高温气体对迎风面上易结冰部位进行加热，从而保证表面不结冰，其优点是技术成熟、可靠；后者则通过水滴撞击特性研究，对旋转帽罩等部件的外形进行优化设计，配合材料或涂层技术来达到防冰目的，这样对整机性能更为有利，同时也能使发动机的结构得到简化。

本文在前人非旋转部件及防冰支板水滴撞击特性计算方法的基础上[3～5]，基于FLUENT，提出了发动机旋转整流帽罩的水滴撞击特性计算方法，并利用该方法对不同帽罩锥体锥角和不同转速下帽罩的水滴撞击特性进行了研究。

2 计算模型与方法

计算对象为航空发动机旋转整流帽罩，其几何外形为锥体(见图1)。锥体长度L为0.52 m，固定不变。考察锥体的上表面，分别对如下两种工况进行研究。

(1)对锥体半锥角为20°时不同帽罩转速(3 000 r/min、6 000 r/min、9 000 r/min)及帽罩静止条件下的局部水收集系数进行比较。

(2)对帽罩转速为6 000 r/min时4个半锥角(15°、20°、25°、30°)的局部水收集系数进行比较。

由于对部件的三维流场进行精确模拟十分耗时，考虑到模型的轴对称特性，在轴向来流条件下，可采用轴对称的方法求解旋转帽罩周围的流场。

2.1 空气控制方程

多重参考模型的粒子跟踪和耦合离散相轨迹模型是基于绝对速度的质点跟踪，基于绝对速度的稳态旋转参考坐标系的连续性方程和动量方程如下：

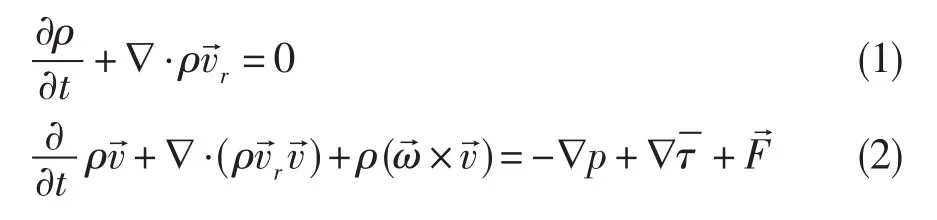
2.2 水滴控制方程

在水滴撞击特性的计算方法上，主要有欧拉法和拉格朗日法[6，7]。拉格朗日法水滴运动方程形式简单，求解方法成熟，因此广泛应用于积冰研究[8]。本文采用拉格朗日法建立过冷水滴的运动方程，并作如下假设：①过冷水滴在流场中均匀分布，且以球形存在，不分解，不变形；②水滴在运动过程中其温度、粘性、密度等介质参数保持不变；③由于水滴密度要远大于空气密度，故忽略由压力梯度引起的力和表观质量力及气动升力。另外，由于重力对局部水收集系数及收集区域的影响很小，可忽略[4]。因此，本文只考虑作用在水滴上的粘性阻力。

在拉格朗日坐标系下，通过分析作用在水滴上的力平衡来确定离散相颗粒的轨迹，由牛顿第二定律可得出水滴运动轨迹。不考虑重力影响时，其方程可表示为：

式中：ua为空气速度；uw为水滴颗粒速度；ρw为水滴密度；dw为水滴直径；Re为相对雷诺数，由下式确定

其中，ρa为空气密度，μa为粘性系数。

2.3 边界条件

求解旋转帽罩周围流场的边界条件设置如下：

(1)来流给定速度边界条件；

(2)出口流场给定压力出口边界条件；

(3)定义旋转轴，给定区域入口处水滴的流动方向和速度，水滴入口速度为自由来流速度；

(4)壁面的速度边界条件给定壁面的旋转角速度。

2.4 局部水收集系数的求解

局部水收集系数β是指微元表面ds的实际水收集量Wβ与该微元表面上最大可能水收集量Wβ,max之比，可以写成：

假设帽罩锥体微元表面ds上水滴的分布密度为ρs，来流处水滴的分布密度为ρ0，则Wβ、Wβ,max可表示为：

则局部水收集系数β可表示为：

采用用户自定义函数(UDF)求取局部水收集系数的算法如下：

气流中含有均匀分布的水滴颗粒，给定含有水滴的进口面积为A，总颗粒数为n，则分布密度为：

若帽罩锥体表面某网格的面积为As，且UDF统计得到网格上的撞击颗粒数为ns，则该网格处水滴分布密度为：

当进口水滴颗粒数n→∞时，有：

2.5 水滴颗粒位置分布

由于计算网格为轴对称，因此进口水滴颗粒要达到均匀分布，需作如下处理。

如图2所示(图中pi代表各水滴颗粒所在的径向位置，ri代表各水滴颗粒所在圆的半径)，若进口水滴分布半径为R，总面积A=πR2。为保证ρ0为常数，则每个颗粒所在圆环的面积应为πR2/n。

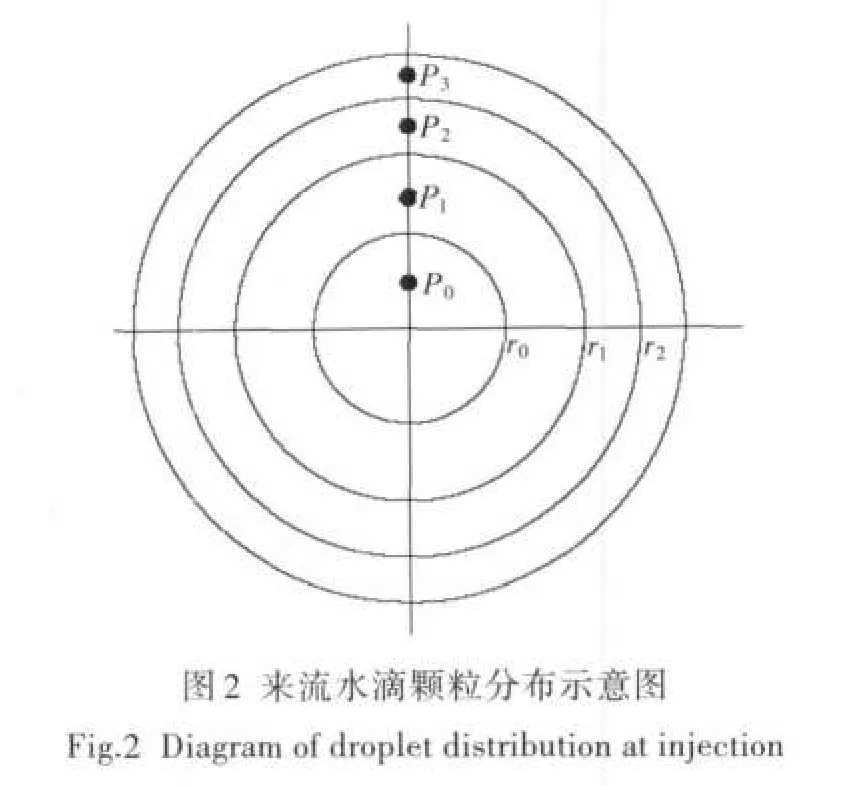
第一个水滴颗粒所在的圆面积为：

第二个圆环面积为：

由此得出各水滴颗粒所在圆的半径ri为：

各水滴颗粒所在的径向位置pi为：

3 结果与分析

航空发动机旋转帽罩研究中，帽罩锥体的锥角和帽罩转速是需要重点考虑的两个因素。本文就不同锥角和转速对帽罩表面局部水收集系数的影响进行分析。

图3是半锥角为20°的帽罩在6 000 r/min转速下的水滴轨迹图。从图中可以看出，过冷水滴在到达帽罩前基本沿水平方向平行前进，在帽罩表面附近开始弯折，然后撞击到帽罩表面。

图4示出了帽罩转速为6 000 r/min时不同帽罩锥体锥角下的局部水收集系数比较。从图中可以看出，帽罩最大局部水滴收集率出现在帽罩顶点附近，且锥角越大，水滴撞击区域就越小，最前端撞击位置就越靠前；锥角越大，帽罩的最大局部水撞击系数就越大，帽罩后部其下降幅度亦越大。在相对坐标(撞击点轴向长度除以帽罩总轴向长度)约0.25后，曲线趋势发生变化，锥体锥角越大，帽罩局部水收集系数就越小。这说明锥角对帽罩局部水收集系数有较大影响。

图5为帽罩锥体半锥角为20°时不同转速下的局部水收集系数比较。从图中看，离帽罩顶点不远处，局部水收集系数变化不大；而在帽罩后部，帽罩转速越大，其局部水收集系数越小，且水滴收集区域越小。这说明转速对局部水收集系数也有很大的影响。

4 结论

本文基于拉格朗日法，利用FLUENT数值模拟软件及UDF接口，提出了计算发动机旋转帽罩表面水滴收集系数的计算方法。研究结果表明，在同一帽罩转速下，随着帽罩锥体锥角的增大，帽罩的局部水收集系数沿帽罩表面外形线下降较快，且撞击区域变小；同一锥角下，随着转速的增加，帽罩表面的局部水收集系数下降，且撞击区域变小。

[1]常士楠.大型飞机的防/除冰问题[C]//.中国航空学会2007年学术年会：机载、航电专题.2007.

[2]张德志.中国大型飞机发动机研制中的关键技术[J].中国民航大学学报，2008，26(5)：26—28.

[3]王 波.涡轴发动机零级导叶热气防冰系统性的计算与实验研究[D].上海：上海交通大学，2007.

[4]闵现花，董 威，朱剑鋆.水滴撞击特性的重力影响分析[J].燃气涡轮试验与研究，2010，23(3)：42—45.

[5]杨 军，郭 文，娄德仓.发动机防冰支板水滴撞击特性的数值研究[J].燃气涡轮试验与研究，2011，24(1)：19—24.

[6]Bourgault Y，Habashi W G，Dompierre J.An Eulerian Ap⁃proach to Supercooled Droplets Impingement Calculations[R].AIAA 97-0176，1997.

[7]杨 倩，常士楠，袁修干.水滴撞击特性的数值计算方法研究[J].航空学报，2002，23(2)：173—176.

[8]Hedde T，Guffond D.Development of a Three-Dimension⁃al Icing Codes,Comparison with Experimental Shapes[R].AIAA 92-0041，1992.