多变量多目标涡轴发动机最优加速控制

颜秋英，时瑞军，周剑波，杨春来，周文祥，2

(1.中航工业航空动力机械研究所，湖南株洲412002；2.南京航空航天大学能源与动力学院，江苏南京210016)

1 引言

随着我国涡轴发动机数字电子控制系统的成功服役使用，深入研究涡轴发动机的加速控制问题、最大限度地挖掘发动机的潜力、提高发动机的性能，已成为当今迫切需要解决的课题。国内对涡扇发动机的最优加速过程进行了较为广泛的研究[1～4]，而对于涡轴发动机的最优加速技术研究还较少，仅有西北工业大学对某型涡轴发动机进行了最优控制技术的初步研究[5]。

目前，非线性规划算法迅速发展，使得其在最优控制理论和工程中受到越来越多的关注[3]。其中，序列二次规划(SQP)算法是当今求解包含约束的中小规模非线性规划问题的最优秀算法之一[6]。近年来，Lawrence和Tits提出了能保证迭代点可行的FSQP算法[7]。该算法直接以目标函数为效益函数，避免了常规SQP算法惩罚因子选择不当对算法的影响，并具有全局收敛和局部超线性收敛特性。因此，本文基于变几何涡轴发动机部件级动态数学模型，提出了利用FSQP算法的加速过程最优控制算法，并仿真研究了涡轴发动机多变量多目标加速过程。

2 FSQP算法

带约束的非线性规划问题描述如下：

式中：目标函数f(x)和约束函数gi(x)均定义为Rn中的二阶连续可微的非线性函数，n为约束个数。

FSQP算法通过迭代算法求解，通过每一步求解下列二次规划问题得到可行性搜索方向dk和γk变量：

式中：0＜Hk=HkT∈Rn×n，0≤ηk∈R。当xk≤X时，求解二次规划所得到的γk≤0，因此dk必然是非线性规划问题(1)的一个可行的下降方向，而ηk是为保证dk满足可行性而加入的修正变量。

FSQP算法中一般采用二阶修正方法来克服Maratos效应，从而保证算法的局部超线性收敛速度。通过求解下列二次规划问题得到dk的校正量

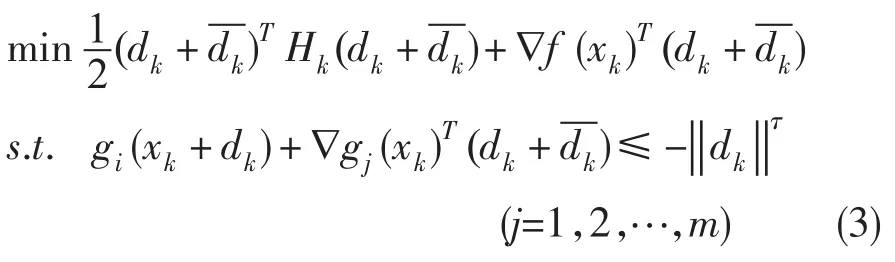
式中：τ∈(2，3)。通过上述方法得到可行的搜索方向后，FSQP算法根据下式获得下一个迭代点：

式中：tk为通过曲线搜索算法所得到的迭代步长，并同时保持下一步迭代点的可行性，即满足xk+1∈X。

3 涡轴发动机最优加速控制算法

本文的研究对象为压气机导叶可调的自由涡轮式双转子涡轴发动机，其控制变量为燃油流量和压气机导叶角度。涡轴发动机加速过程一般要求为：从飞行慢车加速到指定工作状态(如巡航状态)的过程中，加速过程快速，动力涡轮转速下垂较小，发动机工作安全。由此，提出变几何涡轴发动机最优加速算法。

3.1 优化变量

优化变量为涡轴发动机燃油流量mf和变几何压气机导叶角度α。

3.2 优化目标

优化目标是动力涡轮转速下垂或超调量最小，且加速时间最短。

对于自由涡轮式双转子涡轴发动机，动力涡轮转速下垂或超调量最小，可用下面目标函数表示：

式中：np、np,r分别为动力涡轮转速及要求的恒定转速。

加速时间最短，也即燃气涡轮转速上升最快。因此时间最短的优化目标可用下面目标函数表示：

式中：ng、ng,f分别为燃气涡轮转速及加速终了燃气涡轮转速。

由于加速过程要求两个目标函数同时满足，因而必须采用多目标函数的形式。这里采用线性加权法组合上面两个目标函数，构造成的整个加速过程的目标函数为：

式中：w1、w2为线性权重系数，且w1，w2＞0，w1+w2=1。线性加权法的求解特点是对各目标加权后以其线性和作为评价函数，应用简单方便。

3.3 约束条件

在涡轴发动机最优加速过程中，发动机的安全工作最为重要。因此必须保证涡轴发动机排气温度不超温、压气机不喘振、发动机输出功率不超限，同时还应考虑实际的调节变量mf和α的变化率存在物理极限。对应的约束条件为：

4 仿真结果

根据上面提出的涡轴发动机最优加速控制算法，本文分别针对地面和高空的不同目标函数加权系数，仿真研究了涡轴发动机最优加速控制。

4.1 地面加速仿真

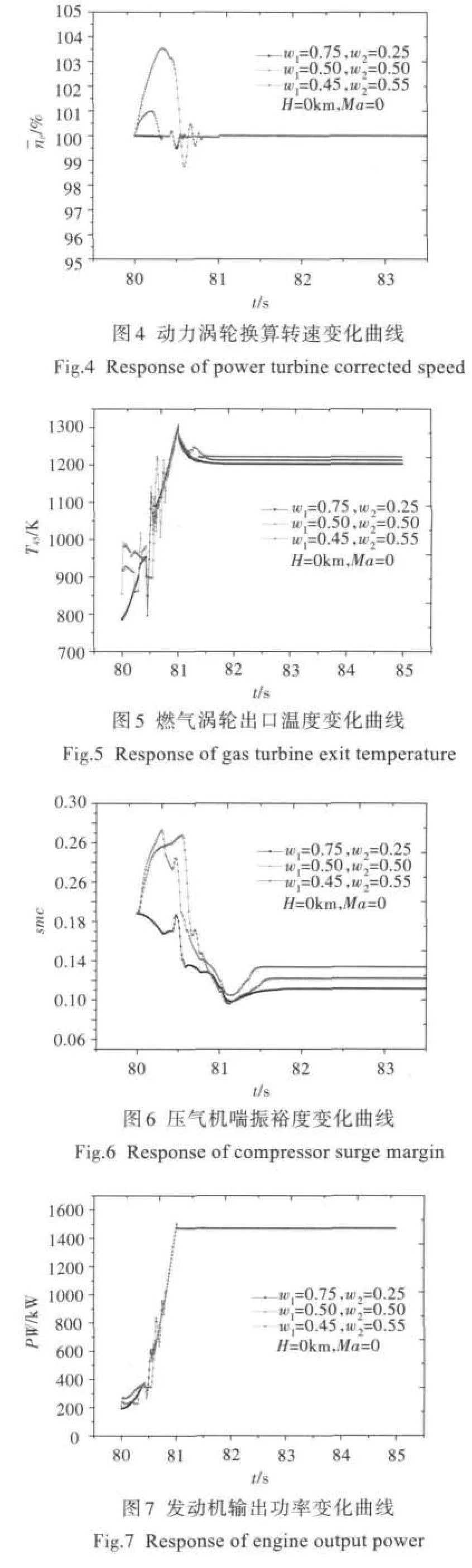
图1～图7 为H=0 km、Ma=0，w1分别为 0.75、0.50、0.45，对应的w2分别为0.25、0.50、0.55时，涡轴发动机从的仿真结果。对应的约束条件分别为

另外，随着w1、w2的不同，仿真效果亦不同。当w1=0.45、w2=0.55时，动力涡轮转速出现3.5%的超调，超调较大；当w1=0.50、w2=0.50时，动力涡轮转速超调1%，燃气涡轮转速增加的速度相对于w1=0.45、w2=0.55的情况更快；当w1=0.75、w2=0.25时，动力涡轮转速控制稳定，没有出现超调，燃气涡轮转速的控制与w1=0.45、w2=0.55时的基本相同，但最终控制压气机喘振裕度最小，控制效果最好。

4.2 高空加速仿真

从图中可以看出，发动机在H=6 km的高空从对应的飞行慢车转速加速到最大状态100%的过程中，燃气涡轮转速、压气机喘振裕度、发动机最大功率、压气机导叶角度变化量、燃油流量变化量均在限制值内。

从图中还可以看出：当w1=0.35、w2=0.65时，燃气涡轮转速为主要控制对象且快速响应，动力涡轮转速出现了1.5%的超调，但燃气涡轮转速的增加相对其它两组更加快速；当w1=0.50、w2=0.50时，动力涡轮与燃气涡轮调节的权重相同，动力涡轮转速基本控制在100%转速；当w1=0.65、w2=0.35时，动力涡轮转速为主要控制对象，燃气涡轮转速的控制权重相对于其它两组较小，但从控制效果来看，动力涡轮转速控制稳定，燃气涡轮转速调节比w1=0.50、w2=0.50时更加快速。

因此，在目标函数权重系数的选择上，应同时考虑动力涡轮转速控制的稳定性和燃气涡轮转速的快速性。以上三种情况下，w1=0.65、w2=0.35时优化效果最好。

5 结论

本文提出了基于FSQP算法的多目标多变量自由涡轮式双转子涡轴发动机的最优加速控制算法，研究了不同加权系数的多目标函数对涡轴发动机加速过程的影响。仿真研究表明，提出的最优加速算法合理、可行，改善了涡轴发动机的加速品质，挖掘了发动机的潜力。

[1]樊思齐，徐芸华.航空推进系统控制[M].西安：西北工业大学出版社，1995.

[2]戚学锋，樊 丁，陈耀楚，等.基于FSQP算法的涡扇发动机多变量最优加速控制[J].推进技术，2004，25(3)：233—236.

[3]吴沧浦.最优控制的理论与方法[M].北京：国防工业出版社，2000.

[4]袁业湘，孙文瑜.最优控制理论与方法[M].北京：科学出版社，2001.

[5]郭腊梅.涡轴发动机最优加速控制研究[D].西安：西北工业大学，2003.

[6]Gill P E，Jay L O，Leonard M W，et al.An SQP Method for the Optimal Control of Large-Scale Dynamical Systems[J].Journal of Computational and Applied Mathematic，2000，120(1)：197—213.

[7]Lawrence C T，Tits A L.A Computationally Efficient Fea⁃sible Sequential Quadratic Programming Algorithm[J].SI⁃AM J.OPTIM，2001，11(4)：1092—1118.