线性代数中矩阵的应用研究

李 明

(苏州工业职业技术学院，江苏 苏州 215104)

线性代数中矩阵的应用研究

李 明

(苏州工业职业技术学院，江苏 苏州 215104)

文章分析和研究了矩阵在不同领域中的应用，并通过实例展现了矩阵应用的广泛性，以及渗透在各个学科中的普遍性，显现了矩阵在解决实际问题中所起到的简化作用，从而能更进一步地研究和推广矩阵的应用性。

线性代数;矩阵;矩阵应用

0 引言

线性代数是高等代数的一大分支，矩阵和行列式是线性代数中最重要的内容。随着计算机的飞速发展和广泛应用，许多实际问题可以通过离散化的数值计算得到定量的解决，于是作为处理离散问题的线性代数就越来越受到世人的关注，并已经渗透到物理学、统计学、计算机科学、人工智能、系统控制论、信息论、图形图像处理、材料化工和农林医学等领域的应用前沿，矩阵已经成为一门独立的理论在各个领域发挥着应用潜能。

矩阵是将重要信息数据摘录下来的一个数表，可以对数据进行各种变换，得到一个新的矩阵，从而通过代数的方法进行研究，对复杂和抽象化的问题进行简化，看清问题的本质，得出一些需要的结论，因此在很多实际应用中都渗透了矩阵理论。为此对矩阵在各学科中的应用实例进行分析和解决，进一步研究和推广矩阵的应用性。

1 矩阵在量纲化分析法中的应用

所谓量纲化分析，最早是在20世纪初物理领域中建立数学模型的一种方法。许多物理量都是有量纲的，它分为基本量纲和导出量纲。基本量纲包括时间[t]=T、质量[m]=M 和长度[l]=L，其他量都是导出量，如，加速度的量纲[a]=LT-2就是由基本量纲导出的。等号两端各变量遵循量纲一致的原则，可以建立一个线性方程组，通过矩阵变换解决量间的关系[1]，如例1。

例1 (勾股定理的证明)设一个RT△的斜边长为c，2个直角边长分别为a，b。假若选取三角形面积S，2个锐角α，β及斜边c为待研究的变量，则必有如下关系:

式(1)有4个量纲，而只有3个基本量纲，必有1个量是无量纲的，将上述各量的量纲列成矩阵如下，每列代表1个变量的量纲数据[2]。

解线性方程:

解之得:x11=2，x21=0，x31=0，故有关系式:

其中，λ为唯一待确定的无量纲量。式(2)说明在RT△中，面积与斜边的平方成比例。假若作斜边上的高，将三角形分成2个相似的RT△，面积分别为S1，S2，则边长a，b成为2个小RT△的斜边[3]，三角形相似图如图1所示。

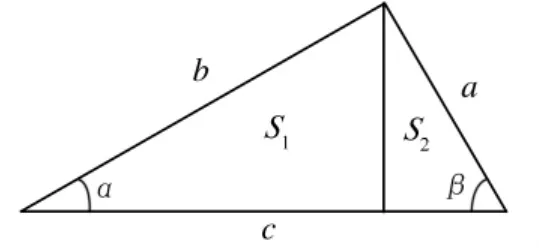
图1 三角形相似图

根据上面得到的结论和相似原理，有S1=λa2，S2= λb2，而 S=S1+S2，则:

λc2=λa2+λb2

勾股定理得证，即:

c2=a2+b2

量纲分析只涉及代数运算，因此人们在做非常昂贵的实验之前，比较倾向于在不同假设下建立若干相似模型，再择优进行，有时还对部分常数起到了压缩或恢复的作用。

2 矩阵在信息编码中的应用

在密码信息传输中，矩阵运算的应用非常广泛，主要是编码和译码。所谓编码是将明文加上密钥加密成密文发送出去，而译码是将密文通过密钥解密成明文。由于两过程是相反的，因此矩阵的逆运算就发挥了较好的作用。

一般通用的传递信息方法是26个字母依次对应1～26个整数，如，A对应1，B对应2，C对应3，等等，依次对应，空格对应0，具体见表1。

表1 字母对应表

密钥是由初等矩阵变换而来的，由于初等矩阵均是可逆矩阵，因此保证了密钥矩阵也是可逆的，且矩阵A中所有元素均是整数，其行列式值为±1，这样可以保证A-1中所有元素也是整数，若明文矩阵B，且信息放在矩阵B的各列，经过密钥A对其加密，AB=C后成为密文C传输。因此，要解密得到明文B，只需左乘A-1，得B=A-1C，如例 2[4]。

例2 (解密算法)若加密密钥为矩阵:

传输出信息为: -19，19，25，-21;0，18，-18，15，3，10，-8，3，-2，20，-7，12，它传输了什么信息?

实际上将密文信息按照列排成密文矩阵:

则明文矩阵B应为:

对应表1得到相应的信息为:DO YOUR HOMEWORK(做作业)。

3 矩阵在经济模型中的应用

商品交换是经济事务中的常事，它在经济社会中时刻都有发生，小到2人之间的实物交换，大到产业之间的交易，都或多或少，或简单或复杂地参入了商品交换中各商品价值的体现，假如不考虑资本积累和债务，交换是封闭式的，如何对已生产出的产品进行合理地定价，才能维持整个经济社会正常的运作?

在这个复杂的经济系统中，矩阵可以将其转化为线性方程组而轻松地解决，如例3。

例3 (商品交换基础模型)假如社会存在3种产业之间的商品交换，这3种产业分别记作E，F，G，它们在不存在货币制度的前提下，使用实物交换制度。产业E将商品的留给自己，给产业F，给产业G。产业F将商品的留给自己，给产业E，给产业G。产业G将商品的留给自己给产业E给产业F。应该如何给这3种产业进行定价，才能使经济体持续进行下去[4]?

根据上述信息，可以构造一个有向图来表示实际实物交换的整个系统，如图2所示。图2中的箭头表示商品在某2个产业之间流出和流入的交换状况。

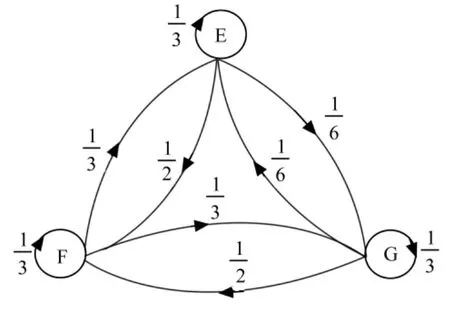
图2 实物交换系统图

将3种产业E，F，G的产品分配情况列成表格，清晰描述如下:

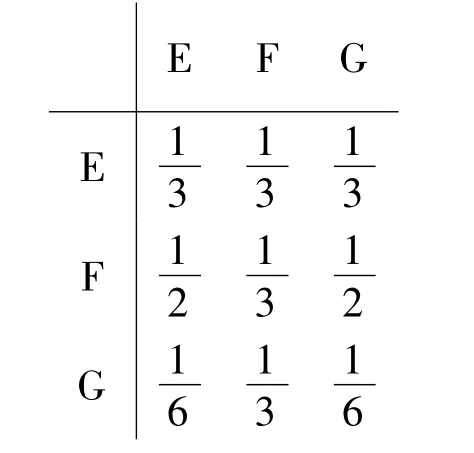
这些方程构成了一个齐次线性方程组:

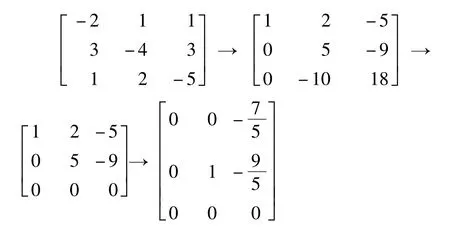
通过矩阵变换，得:

4 矩阵在生物种群生长趋势动态预测中的应用

在研究生物种群发展时，矩阵方程、矩阵乘法和矩阵对角化的知识，能较为容易地解决矩阵高次幂的结果，而矩阵高次幂的运算描述了生物种群若干年后的发展状况，因此矩阵很好地预测、验证、模拟了种群的繁衍情况，如例4。

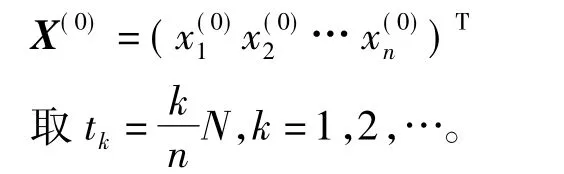
那么，在tk时刻动物种群年龄分布为:

随着时间的变化，种群各年龄段动物的数目也会发生变化，根据平衡关系，时刻tk，第一个年龄组中雌性动物数等于在时段[tt-1，tk]内各年龄阶段中动物生育的幼体数目总和，即:

又由于:

即:

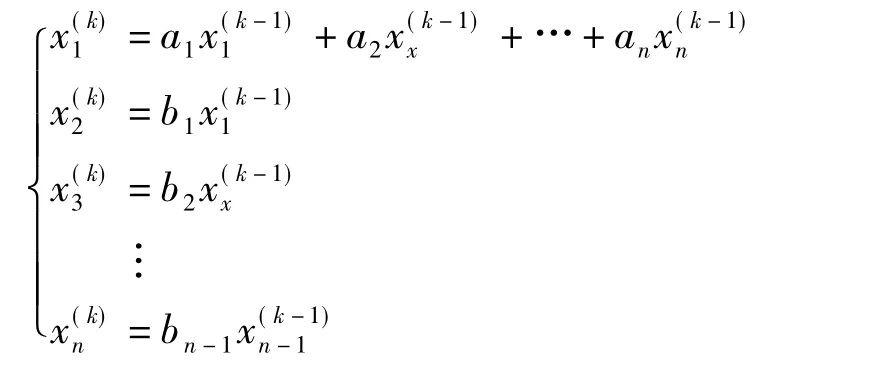
有矩阵乘积 X(k)=AX(k-1)，k=1，2，…，n -1，其中系数矩阵为:

于是，X(k)=AkX(0)，k=1，2，…，n -1。

知道初始时刻，动物种群的年龄分布，就能算出tk时刻种群数目的分布X(k)。

假如，N=15，分成 3 个年龄组[0，5]，[6，10]，[11，15]，统计得 3 个年龄组雌性动物的生育率分别为 0，4，3，存活率为 0.5，0.25，0，初始时刻3个年龄组雌性动物的数量为1 000，1 000，2 000，那么10年后动物总数又如何?[5]

相当于:

说明10年后，3个年龄段的动物总数分别发展为2 750，5 000，250。当 n足够大时，涉及到A″的求解，需要使用矩阵对角化的知识，再通过n→∞时的极限知识来研究动物总数的整个趋势，从而科学地预测和分析动物数量动态的变化过程。

通过不同领域中矩阵的应用实例，说明矩阵正在发挥着它独有的潜能，随着科学技术的发展，矩阵应用的渗透会越来越深入，各个学科之间的交叉会越来越频繁，学科之间的界限也会越来越模糊，数学的基础性会越来越明显，因此，有数学参与的研究会更加有说服力，会更加简洁，矩阵就做到了这一点。

[1]姜启源，谢金星，叶俊.数学建模[M].3版.北京:高等教育出版社.2005.

[2]吴学勇.量纲分析应用研究[J].甘肃高师学报，2000(5):40-43.

[3]孙建美.量纲分析及其应用[J].湖北汽车工业学院学报，2001(15):60 -62，80.

[4](美)Steven J Leon.Linear Algebra with Applications[M].8th ed.张文博，张丽静，译.北京:机械工业出版社，2010.

[5]黄玉梅，彭涛.线性代数中矩阵的应用典型案例[J].兰州大学学报:自然科学版，2009，45(专辑):123 -125.

Study on the Application of Matrix in Linear Algebra

LI Ming

(Suzhou Institute of Industrial Technology，Suzhou 215104)

This paper makes an analysis of the matrix in four different fields of application，and cites examples to demonstrate the popularity of matrix application and its penetration in all disciplines.It demonstrates the simplifying function of matrix in solving practical problems，thus to further the research and extension of matrix application.

linear algebra;matrix;matrix application

O151.21

A

1671-0436(2011)03/04-0059-04

2011-07-04

李明(1975— )，女，硕士，讲师。

责任编辑:张秀兰