基于SVM的桥区水域失控船舶航迹研究*
王艳锋
(武汉交通职业学院,湖北 武汉 430065)
0 前言
随着公路、铁路建设高潮的到来,我国跨海、跨江桥梁的数量出现了突飞猛进的增加。桥梁数量的增加同时也对船舶的航运安全造成一定的影响,船舶撞桥事故屡屡发生。船撞桥事故在世界各地一直在不断地发生,船撞桥事故的频率远比我们的想象更经常。由船撞桥事故所导致的人员伤亡、财产损失以及环境破坏是极其惊人的。很多船舶撞桥事故轻则损失数万元,重则人员伤亡、损失以数百万、数千万甚至数十亿美元计,大量的间接损失更是难以计算。船舶在桥区水域失控时,在风、流以及惯性力的影响下,能够有效预测出未来一段时间内船舶运动的轨迹,这样就可以提前采取有效措施降低损失,甚至可以避免交通事故发生。
1 船舶失控原因分析
根据《国际海上避碰规则》中失控船舶的定义:“失去控制的船舶”指由于某种异常情况,不能按《1972年国际海上避碰规则》条款的要求进行操纵,因而不能给他船让路的船舶。“某种异常情况”主要是指船舶本身的异常情况,如主机或舵机发生故障,车叶或舵叶丢失或者严重损失等;某种异常情况也包括某些客观原因造成的异常情况,如风大流急造成船舶走锚,大风浪中船舶卸锚抛链滞航等。因此,造成船舶失控的原因可以分为人为因素、船舶设备因素以及自然环境因素:
(1)近年来,随着航运经济的飞速发展,船舶数量激增,船员市场已经无法满足航运业的发展要求。船员尤其是高等级船员人员紧缺,船员流动性比较大。培训船员以及船员培训机构良莠不齐,造成部分船员素质达不到合格要求。
(2)船舶应急设备平时缺乏系统保养,长时间不使用,关键时刻无法发挥关键性作用。
(3)船舶设备老化,保养更新不及时。老龄船舶的设备由于长期使用,设备耗损大、线路老化等故障较多,如果维修保养不及时,容易酿成失控事件。
2 支持向量机(SVM)理论
2.1 统计学理论
统计学习理论是建立在一套较为坚实的数学理论基础之上的,为解决有限样本学习问题提供了一个统一的框架。它能将很多现有的方法纳入其中,帮助解决许多原来难以解决的问题(比如神经网络结构选择问题、局部极小点问题等);同时,在这一理论基础上发展了一种新的通用机器学习方法——SVM方法,它已初步表现出很多优于已有方法的性能。一些学者认为,SLT和SVM正在成为继神经网络研究之后新的研究热点,并将推动机器学习理论和技术的重大发展。
机器学习的目的是根据给定的训练样本求取系统输入、输出之间依赖关系的估计,使它能够对系统行为做出尽可能准确的预测。机器学习问题的基本模型可以用图1表示。

图1 机器学习模型
2.2 SVM的实现
SVM是Cortes和Vapnik在1995年首先提出的,它在解决小样本、非线性及高维模式识别中表现出许多特有的优势,并能够有效推广应用到函数拟合等其他机器学习问题中。
SVM与其它传统的机器学习方法相比,它具有以下的一些优点:
(1)它是专门针对有限样本情况,其目的是在现有信息下得到最优解而不仅仅是当样本趋于无穷大时的最优解。
(2)以严格的数学理论(统计学习理论)为基础,采用结构风险最小化原则,克服了传统神经网络学习中靠经验和启发的先验成分等缺点,提高了置信水平,克服了学习等问题,使学习机器具有良好的泛化能力。
(3)SVM算法最终将转化为一个二次型寻优问题。从理论上说,得到的将是全局最优点,解决了在神经网络方法中无法避免的局部极值问题。
(4)算法将实际问题通过非线性变换转换到高维的特征空间,在高维空间中构造线性判别函数来实现原空间中的非线性判别函数,其特殊性质能保证机器有较好的推广能力,同时它巧妙地解决了维数问题,其算法复杂度与样本维数无关。
(5)通过引入VC维概念,使网络收敛速度、样本被错分的界和风险泛函得到控制。
3 桥区水域失控船舶航迹预测模型实现
3.1 预测指标数据的获取
(1)在江阴大桥水域航行的船舶必须遵守长江下游船舶定线制的规定。根据在江阴海事局所取得的调研资料表明,船舶常在江阴大桥上游61号红浮、桥梁下游60号红浮附近出现失控现象。长江为一级航道,根据桥区水域的界定,江阴大桥上游3km至下游2km均为江阴大桥桥区水域。因此,船舶在桥梁上游61号红浮、下游60号红浮附近失控时,均在桥区水域内,对桥梁以及桥区水域的通航安全存在一定的威胁。
(2)桥区水域失控船舶航迹预测需要船舶在桥区水域失控漂移时,船舶的船速、航向,风速、风向以及流速、流向数据位基础上进行。
3.2 失控船舶航迹预测指标的选择
3.2.1 失控船舶航迹预测数据的选取
(1)选取失控船舶的代表船型:由于受到条件的限制,本文选取的代表船型为江阴海事部门巡逻艇,船长20.00m,船宽4.30m,型深2.10m;满载排水量26.00T,总吨位36T,净吨位10T,内燃机410.00KW。
(2)选取船舶失控的地点:本文所采用的数据统计地点为江阴大桥上游。
(3)测试时间:2010年4月20日下午3:30开始,测试地点为31°56.477′N 120°15.912″E,当天风速、风向为4级NE,流速为1.54m/s。流向为EE,初始船速为8kn航向116°。采集到的船舶漂移经纬度数据见表1。

表1 实船实验船位数据
3.3 江阴大桥船位失控船舶航迹预测
3.3.1 SVM网络模型的建立(见图2)
模型目的:利用SVM建立的回归模型对桥区水域失控船舶航迹进行回归拟合。
模型假设:假设在给定风速、风向,流速、流向,初始船速、船向情况下,每隔5s钟测试得到的纬度值(y)与前一5s的纬度值,经度值相关,即把前一时刻的纬度值,经度值作为这一时刻纬度值的自变量,这一时刻的纬度值作为因变量。
其函数表达式为:y=F(前一时刻纬度值,经度值)=F(x)。
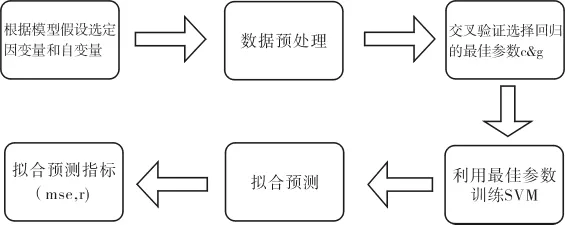
图2 基于libsvm工具箱的网络模型流程图
3.3.2 预测步骤
本文所采用的预测步骤流程图如图3所示:

图3 预测流程图
3.3.3 失控船舶回归预测分析
利用上述回归预测原理对失控船舶船位实船实验回归预测结果如图4所示:
根据失控船舶在江阴大桥水域航迹回归预测分析结果图,可以看出,失控船舶在失控前期和失控后期,误差比较大,说明了船舶在失控过程中的受力情况为:前期船舶由于受到三个力的作用,而且受力不均匀导致船舶在运动过程中出现误差量较大,船舶在运动一定时间和距离后,惯性作用力逐渐降低,而风、流的作用力以及在船舶上的作用点在不断变化,致使失控船舶在测试后期出现了较大的误差量。也说明了失控船舶的运动状态、受力情况是随着自然条件(风、流)的不断变化而变化的。
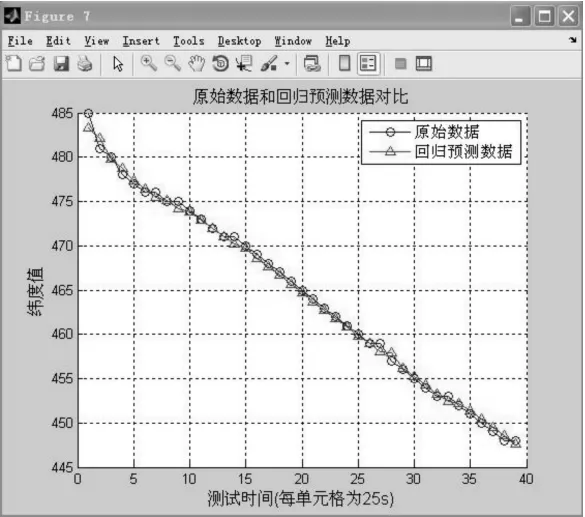
图4 失控船舶船位实船实验回归预测结果图
4 结语
桥区水域失控船舶航迹预测可以有效避免重大水上交通事故的发生。本文通过在江阴大桥桥区水域实船实验数据分析,验证了支持向量机(SVM)在失控船舶航迹回归预测的可行性,为以后失控船舶航迹预测提供相应的理论依据。
[1]交通部.长江江苏段船舶定线制规定(2005)[Z].交海发(2005)417号.
[2]刘明俊,李世刚,等.船舶失控后运动状态分析[J].船海工程,2005,(2).
[3]程志友.桥区船舶失控漂移航迹计算机模拟研究[D].武汉理工大学硕士论文,2007.
[4]刘万里.支持向量机中若干问题及应用研究[M].西安电子科技大学,2008.
[5]Nello Cristianini,John Shawe-Taylor.支持向量机导论[M].北京:电子工业出版社,2004.

