形面测量误差频域阈值处理方法

吕东方，张立富，刘奇晗

（1.黑龙江大学 机电工程学院，哈尔滨 150080；2.哈尔滨工业大学 媒体技术与艺术系，哈尔滨 150001）

0 引 言

在激光扫描测量物体形面过程中，测量数据由于受到测量仪器精度和物体表面性质、形状的影响，不可避免的在数据中混有测量误差。由仪器引入的数据测量误差可以通过对仪器校准来减小，而由被测物体表面特征，如颜色、粗糙度，材质和形状等因素引入的测量误差，校准的方法复杂、实用性差。如何有效地消除误差，提取被测物体形面特征是轮廓测量的重要研究内容[1]。形面测量数据点数目庞大，为了避免人为因素的影响，保证测量数据拟合精度需要采用适当误差处理算法自动处理测量数据[2]。

形面测量数据是通过测量设备对物体表面扫描测量得到的，是随时间和空间连续的变化数据序列，因此可以通过比拟的方法将测量数据当作一维“信号”进行分析，将测量数据中的误差与信号中的噪声相对应。本文采用小波阈值方法针对扫描测量轮廓数据进行处理和多尺度分析，对原始测量数据中包含的各种频率成分进行分解，采用不同阈值方法对数据中的随机误差和粗大误差进行处理，提取被测形面特征，评定测量误差处理质量。

1 小波阈值原理

小波变换的基本思想是用一系列函数去逼近一信号或函数，这一系列函数称为小波基，它是由小波经过伸缩和平移得来的。利用小波分析去噪，即在不同尺度下作小波变换，其实质就是用不同中心频率的带通滤波器对信号进行滤波，把反映噪声频率尺度的小波变换去掉，即可得到质量较好的有用信号。对任意信号，离散小波变换的第一步是将信号分为低频部分（近似部分）和高频部分（细节部分）。近似部分代表了信号的主要特征。第二步对低频部分再进行相似运算，这时尺度因子已改变，依次进行到所需要的尺度[3]。

信号的离散小波变换及重构可利用Mallat算法实现，原始信号x（t）的某层小波分解是将x（t）以某个尺度j变换到空间L2（R）的两个正交子空间Vj和Wj上，由Vj得到离散逼近值aj（k），由Wj得到离散逼近值dj（k），下一层分解中是以尺度j＋1再将aj（k）分解到子空间Vj＋1和Wj＋1中，这样不断分解下去，从而对信号进行了多分辨率的分解。aj（k）对应着信号的低频成分；dj（k）对应着信号的高频成分。

若令aj（k），dj（k）是多分辨率分析中的离散逼近系数，h0（k），h1（k）是满足二尺度差分方程的两个滤波器，则aj（k），dj（k）存在如下递推关系[4]：

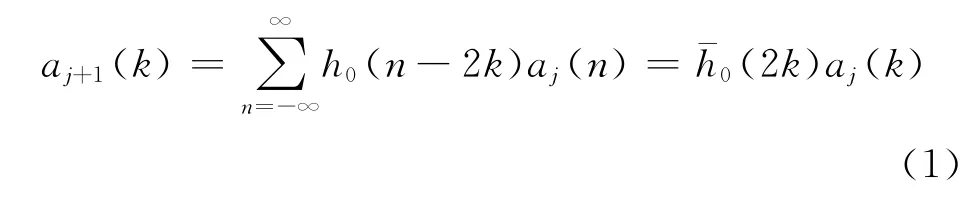
若aj＋1（k），dj＋1（k）分别按式（1）和式（2）得到，则aj（k）可由下式重建：

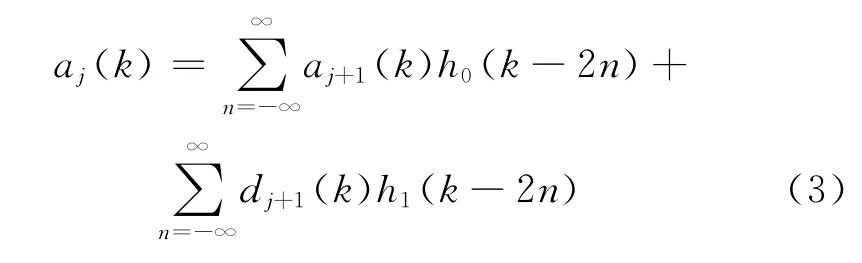
2 误差处理方法

2.1 粗大误差点去除方法

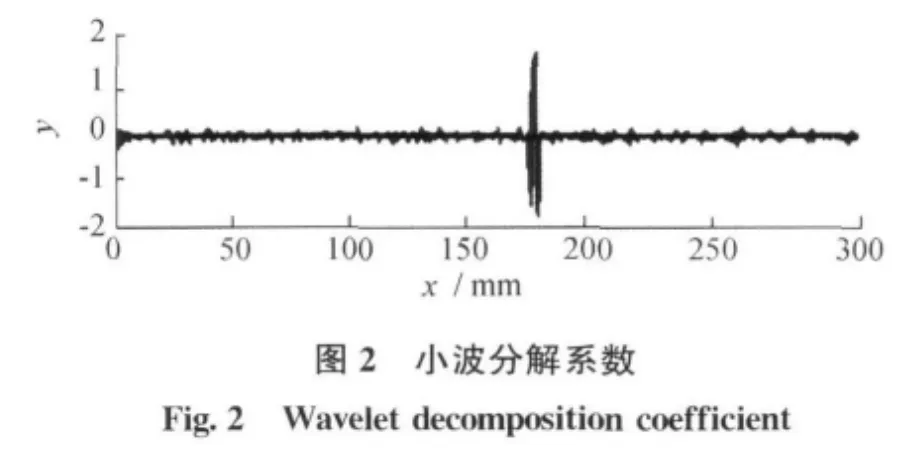
在测量数据处理中，误差数据点数量少，分布稀疏。图1为含有一个粗大误差点的测量数据，其中x轴为测量距离，y轴为形面高度。对图1中的测量数据进行小波分解，得到图2所示的第一层小波高频系数，其中横坐标与图1中测量点位置对应，纵坐标为对应点的小波分解系数。由图2可见，对应粗大误差点，高频信号有一个明显的脉冲突变，利用这个突变脉冲可以准确地检测到粗大误差点的位置，并将其剔除[5]。噪声在高频分解系数中表现为高斯噪声，而粗大误差在分解系数中表现为一系列的尖峰。对尖峰信号的去除采用3σ准则对每层的阈值进行提取，小波系数＞3σ的则认为是粗大误差予以剔除，剔除方法如下：

计算均方值

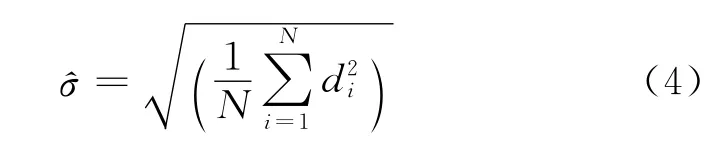
求｜di｜（i＝1，2，…，N）的最大值｜d｜max，若｜d｜max＜，则认为没有粗大误差。

剔除｜d｜max。

对小波分解的每一层的高频系数都做同样的处理，重复上述步骤，直到没有＞的系数，此时求出的为噪声的均方值。通过此方法的处理后，粗大误差基本可以消除。

2.2 减少随机误差方法

小波系数阈值去除随机噪声的方法分为硬阈值法和软阈值法。硬阈值法会产生间断点，得不到理想的降噪效果；软阀值方法中阀值函数在小波域内是连续的，但是它的导数是不连续的，并且软阈值对大于阈值的小波系数采取恒定值压缩，这与噪声分量随着小波系数增大而逐渐减小的趋势不相符。

针对软阀值函数的缺陷采用渐近阈值函数，其函数表达式为：

由此可见函数式（5）是以直线y＝x为渐进线的。当阈值很小时，新阈值函数的作用与硬阈值函数相当，但它更灵活，当｜x｜非常接近阈值λ时，不是直接将小波系数置零，而是渐近为零，这样就使得函数连续，为进一步利用该函数提供了可能。

该阈值函数图见图3，阈值λ为10。｜x｜＜λ的小波系数域内置零，在｜x｜≥λ时，函数对小波系数采取缓变压缩，随着小波系数的不断增大，压缩量减小。当小波系数大于一定值时，不进行压缩处理。通过采用各个尺度下不同的阈值，自动地调整阈值函数，使得调整后的阈值函数更加适应该尺度下的阈值处理，比通用的软阈值去噪有更好的去噪效果。

图3 阈值函数对比图Fig.3 Threshold function comparison

3 实验结果

数据去噪的目标是降低噪声的同时尽量保持原始数据的完整。在实际应用中，通常采用信噪比衡量小波的去噪效果。信噪比是衡量测量信号中的噪声量的传统方法，常用来作为去噪效果的评价标准，信噪比单位为分贝（dB），其定义为：

小波母函数采用4种常用的离散小波函数系：Symlets小波系，Daubechies小波系，Coiflet小波系和Biorthogonal小波系，以去噪后的信噪比为指标，对其进行了基于小波变换的信号去噪处理实验，以评价各种小波函数在阈值选取方法相同时对噪声滤波效果的优劣。在大多数情况下，采用5层分解去噪后可以得到比较满意的信噪比，因此在实验中采用的小波分解层数为5层。图4为用于检验小波去噪算法的实验数据，对该数据进行小波去噪对比实验。

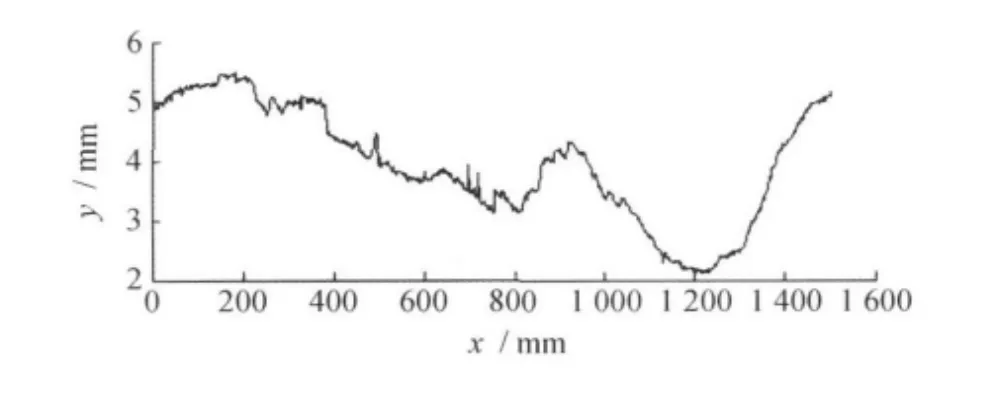
图4 实验数据Fig.4 Test data

渐进阈值函数的软阈值去噪来降低随机误差，上一节中已经论述了该函数的基本性质，基于该函数的阈值λj为：

式中j为分解尺度；N为信号长度；σ为该分解尺度下噪声的标准差。

对图6中含有随机误差的数据采用基于渐近阈值函数的软阈值去噪来降低数据中的随机误差，处理后的测量数据重构见图7，图7显示数据中的粗大误差点和噪声点已经得到了很好的消除，并保留了数据的形状特征。

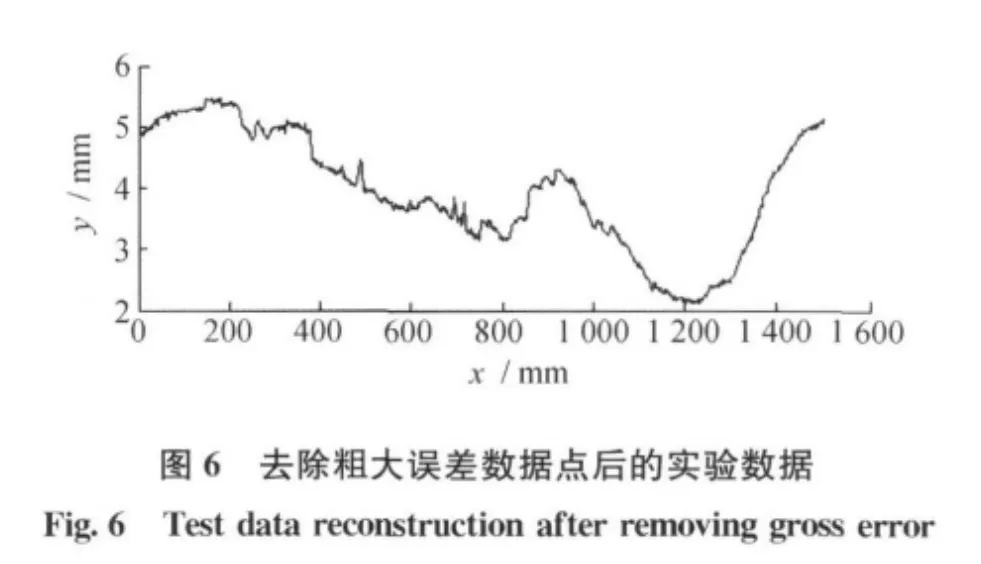
在常用的小波基函数下对比采用传统的软阈值方法、硬阈值方法和本文的阈值去噪方法对实验数据的处理结果见表1，综合去噪是指本文采用的方法。

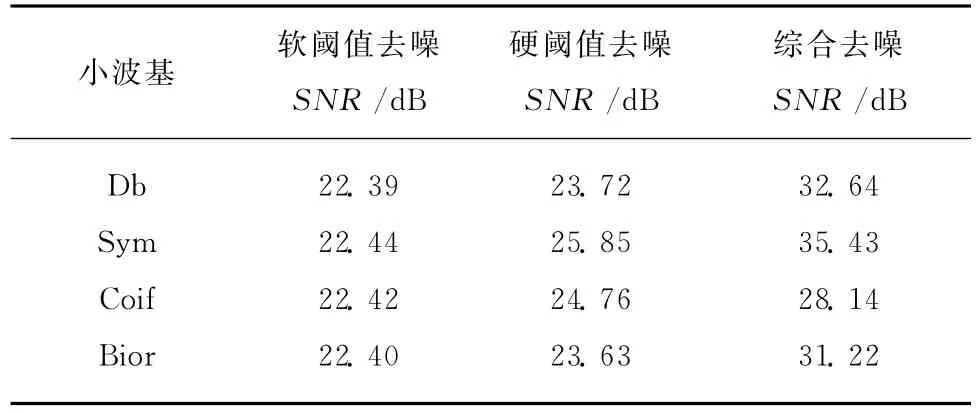
表1 小波阈值去噪效果Table1 Wavelet threshold de-noising result

4 结 论

数据误差处理是形面测量的重要研究内容，也是保证形面重构精度的基础。本文将形面测量数据与信号的离散化相比拟，应用信号的去噪方法对测量数据误差进行处理。在小波变换的基础上，对数据中粗大误差和随机误差采用不同的阈值算法。从实验对比结果看，本文的阈值去噪算法可有效减小形面测量中的测量误差。

[1]Armin Gruen and Devrim AkcaT.Least squares 3Dsurface and curve matching [J].Photogrammetry ＆ Remote Sensing，2005，59：151-174.

[2]Song Zhang.Recent progresses on real－time 3Dshape measurement using digital fringe projection techniques[J].Optics and Lasers in Engineering，2010，48：149-158.

[3]Yong Wu，Yuanjun He，Hongming Cai.Optimal threshold selection algorithm in edge detection based on wavelet transform [J].Image and Vision Computing，2005，23：1159-1169.

[4]Feng Liu，Xiao E.Ruan.Wavelet－based diffusion approaches for signal denoising [J].Signal Processing，2007，87：1138-1146.

[5]Albert C.To and Jeffrey R.Moore.Wavelet denoising techniques with applications to experimental geophysical data [J].Signal Processing，2009，89：144-160.