基于改进单神经元的PET吹瓶机温度解耦控制系统研究

李元伟，王钦若，李 近

（广东工业大学 自动化学院，广州 510006）

0 引 言

在人类的环保意识不断觉醒的今天，低碳经济，节省能源，减少污染已经成为衡量产品优质与否的一个重要指标。而PET瓶正具有节能环保，运输储存方便等诸多优点，使得PET瓶成为了包装容器的一大主流。生产PET瓶当然离不开PET吹瓶机，在PET吹瓶设备中，加热环节是一个关键环节，温度控制得合理，可使PET瓶吸热率最高，这会节约能耗且免受外界环境温度变化的影响。

神经网络控制不依赖控制对象精确的数学模型，是处理控制系统中不确定性、非线性和强耦合的一种有效方法。本文针对吹瓶机温度控制系统的特点，采用基于单神经元的PID解耦控制，得出了实际的仿真结果及结论。

1 吹瓶机温度控制系统的建模

目前高速PET瓶胚加热过程采用 “4段炉体，9段加热，循环风冷，紧凑排列”工艺。加热炉设计主要是满足瓶胚加热到理想的温度，便于拉伸和吹瓶工艺的实现。根据PET的性能，使用9层红外线灯管对瓶胚辐射加热；加热过程中，根据瓶胚质量、厚度和瓶形情况，合理分配每层灯管的加热功率，使瓶胚得到最理想的热量分配。为防止瓶坯过度加热、表面结晶和保护瓶口螺纹及颈环之间的部位不变形，需要用散热风扇对坯口和坯身进行空气冷却。根据以上分析，在吹瓶机温度控制系统中，两个输入量是红外线灯管的电压u1和散热风扇的电压u2，两个输出量为瓶胚的温度y1与散热风扇的风速y2。其中散热风扇的风速对瓶胚的温度有很大的影响，而温度对风速也有一定的影响，所以这是一个耦合系统。根据系统的控制要求，该控制系统可以转化为一个二输入／二输出的被控对象，该被控对象的传递函数框图见图1。

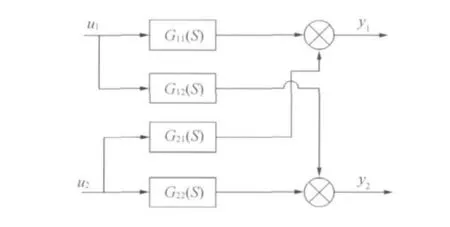
图1 系统被控对象传递函数框图Fig.1 Transfer function block diagram of system controlled object

要对该系统进行解耦设计，首先要知道被控对象的数学模型。采用阶跃响应法来求取相关过程的数学模型。根据实验数据，可以得出被控对象的传递函数为：

2 基于单神经元的PID解耦控制器

神经网络作为一门交叉学科，以其强大的非线性映射能力、并行处理能力、自学习能力，在控制领域得到广泛地应用。采用神经网络的自适应控制方法，计算量是比较大的。由于目前还没有相应的实用型神经网络计算机硬件支持，将多层神经网络自适应控制投入实时在线控制还有一定困难[1]。为了适应快速过程控制系统的要求，采用基于单个神经元的自适应控制。它既可以利用神经网络的优点，又能适应快速过程实时控制的要求。

单神经元是一个具有自学习和自适应能力的多输入单输出的非线性处理单元，可利用单神经元实现自适应PID控制。通过采用多个单神经元PID控制，可以实现对多变量系统的解耦控制[2]。图2给出了二变量单神经元PID解耦控制系统框图，该系统由两个单神经元PID控制器构成。

图2 二变量单神经元PID解耦控制系统框图Fig.2 Flow chart of single neuron PID decoupling control system with two variables

以第一个单神经元PID控制器为例，其控制器框图见图3。

图3 基于单个神经元的PID控制器框图Fig.3 PID controller flow chart based on single neuron

由图3可见r（k）为设定值，y（k）为被控制对象的输出，经微积分模块计算的3个量x1（k），x2（k），x3（k）成为神经元学习和控制所需要的状态变量[3]，它们分别是：

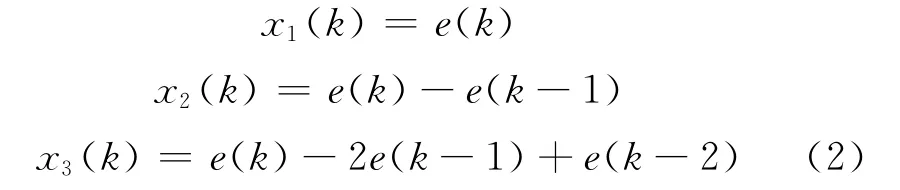
图中K为神经元的比例系数，K＞0；Δu（k）为k时刻神经元的输出值，因此神经元通过关联搜索产生的控制信号u（k）为：

单神经元自适应控制是通过对加权系数的调整来实现自适应、自组织功能的。加权系数的调整可以采用不同的学习规则，从而构成不同的控制算法。在采用有监督的Hebb学习算法时有：

这是文献 [4]的权值学习算法。根据实际的调试结果总结，PID参数的在线学习修正主要与e（k）和Δe（k）有关。因此，本文对加权系数的调整使用改进的有监督的Hebb学习规则，即用e（k）＋V（k）代替xi（k），这是本文的创新点，与文献[4]的学习算法不同，因此可以得到新的学习算法如下：

式中wi（k）为对应于xi（k）的加权系数；θp，θi，θd分别为比例、积分、微分的学习速率，对其采用不同的数值，以便对不同的权系数分别进行调整；K为神经元的比例系数，K值的选取很重要。K越大则快速性越好，但会引起超调量增大，甚至可能使系统不稳定。当被控对象的时延增大时K必须调小，以保证系统的稳定。但K值选择过小，会使系统的快速性变差[4]。

关于选择加权系数初值的问题，由于神经元有自学习功能，它的赋值并不影响加权系数以后的学习结果，也不会影响控制器的控制效果，所以加权系数的初值可以选择较小的随机值。

3 吹瓶机温度解耦控制系统的仿真研究

设采样周期T＝0.1s，将被控对象的传递函数模型即式（1）转化为差分方程，可以表示为：

根据上述的单神经元PID解耦控制原理，控制算法如式（4）所示，我们可以利用Matlab软件搭建如图4所示的Simulink仿真框图来实现该控制器，其中的解耦控制算法部分用S－函数编写，选择S－函数模块的输入信号为 [e（k），e（k－1），e（k－2）]，输出信号为控制量u（k），并将系统被控对象的差分方程封装成一个模块[5]。

图4 单神经元PID解耦控制系统仿真框图Fig.4 Simulation chart of single neuron PID decoupling control system

给定输入信号为单位阶跃输入，即：

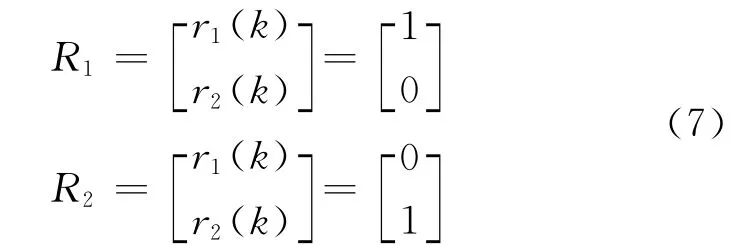
输入信号r1（k）和r2（k）分别对应温度给定值和风速给定值，相应的输出分别为y1（k）和y2（k），R1和R2的单位阶跃信号都是在t＝1 s时加入，仿真时间t＝1000 s。单神经元的参数配置如下：学习速率θp1＝θp2＝0.4，θi1＝θi2＝0.4，θd1＝θd2＝0.4；比例系数K1＝K2＝0.16。当输入信号为R1时的解耦响应曲线见图5，当输入信号为R2时的解耦响应曲线见图6。从图5、图6可以看出，无论输入信号是R1还是R2，采用基于改进单神经元的PID控制器时，系统响应速度快，没有超调，自适应能力强，较好地实现了解耦控制的要求。同时，当输入信号为R1时，在t＝500 s时，对r2（k）即风速给定加入一个幅值为5，持续时间为1 s的脉冲干扰信号，系统的解耦曲线见图7。从图7可以看出，风速值能够较快恢复原来的状态，而温度值不受影响，表明该系统具备较强的抗干扰能力。

4 实际调试结果

图7 有干扰信号时的解耦响应曲线Fig.7 Decoupling response curve with interfering signal

针对PET吹瓶机温度控制系统，我们采用红外温度采集装置采集瓶胚的温度，利用风速传感器测量风速，将信号送到嵌入式控制器，利用本文的单神经元控制算法编写控制程序，对温度和风速进行解耦控制。实际调试结果表明，当改变给定风速时，通过神经元的学习调整，温度仍然保持原来的给定值，达到了解耦控制的要求。

5 结 论

本文采用了基于单神经元的神经网络控制器，并对单神经元的权系数的修正提出了一种改进算法，使权系数的在线修正不完全根据神经网络学习原理，而是参考实际经验制定。仿真及实验结果表明，该方法通过自主学习，调整网络权值，获得良好的解耦控制效果，并且具备较强的抗干扰能力，实现了对吹瓶机加热炉温度和散热风扇风量的精确控制。同时，该神经元控制算法可以推广应用于多变量系统的解耦控制中。

[1]刘 毅，张国忠，吴 俊，等.基于单神经元的温度解耦控制系统研究 [J].微计算机信息，2008，（34）：6-8.

[2]柴天佑.多变量自适应解耦控制及其应用 [M].北京：科学出版社，2001.

[3]薛定宇.控制系统计算机辅助设计-MATLAB语言与应用：第二版 [M].北京：清华大学出版社，2006：223-231.

[4]杨 磊，吴 勇，武 卫，等.基于单神经元PID的航空发动机解耦控制 [J].微计算机信息，2010，（1）：57-59.

[5]刘金琨.先进PID控制及其 MATLAB仿真：第二版[M].北京：电子工业出版社，2004.