新型混沌振子检测微弱光电信号幅值研究

瞿晓东，徐艳春，庞桂云，王立晶，赵月容

（黑龙江大学 机电工程学院，哈尔滨 150080）

0 引 言

在光学系统中，光源经分光片分光后能量更低，大多淹没在噪声中，有用信号极其微弱，所以欲了解微弱光电信号的辐射特性，必须在强噪声中将弱小的光电信号提取出来。目前常用的混沌振子检测微弱信号幅值的方法还是局限在传统的Duffing方程上[1－3]，但由于其结构简单，其动态特性具有一定的局限性。本文在详细研究典型混沌振子动态特性的基础上，尝试将复杂的Lorenz混沌方程和Rösslor混沌方程应用到强噪声背景下微弱光电信号幅值检测中，旨在探索检测微弱光电信号幅值的新方法。

1 Lorenz混沌振子检测微弱光电信号的原理

气象学家Lorenz在上世纪60年代初期，对一个强化的气侯模型进行计算机实验发现了Lorenz混沌系统[4－5]，该数学模型的形式如下：

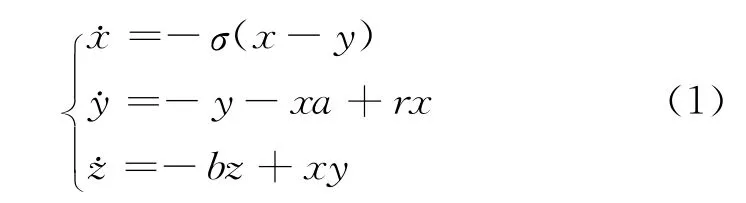
式中σ为普兰特数；r为规范化的瑞利数；b为和域的几何形状有关。

这些参数最普遍的取法是σ＝10，r＝28，b＝8／3，该方程中没有随机的因素，其解完全由参数和初始条件确定，但却很难预测它们的特性。

从该系统可以看出，总有x＝y＝z＝0，3个解，此外当r≥1时还有解z＝r－1，当r＝28时，其轨道相互缠绕，并在过渡衰减之后，时间遍历的复杂几何图形没有自相交，它没有解析解。方程中x、y、z均无量纲，任意给定初值，系统最终都会回到状态空间的特定区域内，其吸引子由指数发散的邻近轨线表征，演化是非周期的，具有精巧而奇特的结构，此时系统进入混沌状态，这就是著名的蝴蝶效应，相轨迹见图1。

蝴蝶效应表明，初始条件的极细微变化随着时间的推移会显著地影响系统的宏观行为，反映在状态空间中。初始状态非常接近的二条轨道，在很短的时间内靠的比较近，然后会迅速散开，如果根据初始状态预测系统的长期行为，会由于误差的迅速扩大，使长期行为的预测受到根本的限制。由此也说明混沌系统具有长期不可预测性。

2 Rössler混沌振子检测微弱光电信号的原理

Lorenz系统是第一个被广泛研究的来自于微分方程的混沌系统。在Lorenz吸引子中有一个关于z轴的对称性，即将（x，y，z）改为（－x，－y，z）时方程不变，因此如果（x（t），y（t），z（t））是系统的解，则（－x（t），－y（t），z（t））亦是系统的解。正是这种对称性产生了Lorenz吸引子的美，然而这种对称性并不是必需的。德国科学家洛思勒（Rössler）在研究洛伦茨系统时发现了一种途径：从更简单的非线性微分方程中产生混沌吸引子[6－8]。

Rössler于1976年给出如下方程：

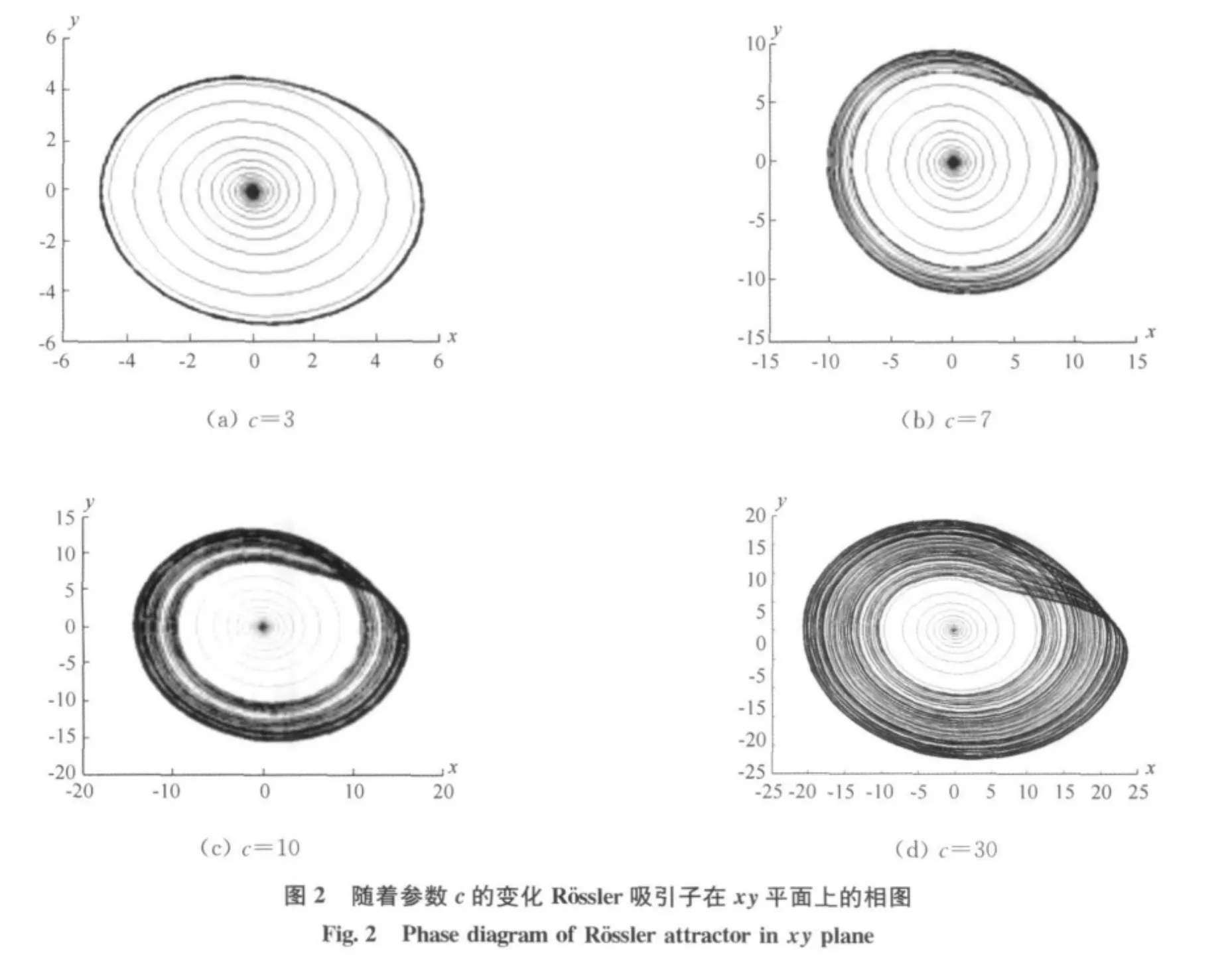
当参数a＝0.373，b＝28，参数c变化时，Rössler吸引子的相图见图2。

当参数a＝0.373，b＝28，c＝10时，xz相图和yz相图投影以及三维相图投影见图3。

3 Lorenz系统相图法进行微弱信号幅值检测

理论上来说，将待测信号加入任一方程中，均可检测信号幅值，仿真实验中，将待测信号加入到Lorenz系统的第一个方程中进行检测，检测步骤如下：

1）固定参数α＝10，γ＝28，β＝24.0061，并在系统中加入均值为0的高斯白噪声n（t），噪声方差为0.01；加入噪声后系统相轨迹见图4。

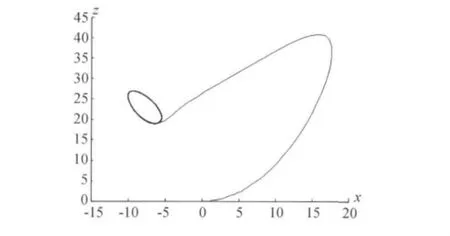
图4 加入噪声后系统xz平面相图Fig.4 Phase diagram when the noise put in xz plane

由图4可见，系统的相轨迹基本没有变化，说明加入均值为零的白噪声不会改变系统的动力学特性，噪声几乎对系统的输出没有影响。这验证了Lorenz混沌系统对噪声具有免疫力。

2）当参数α＝10，β＝24.0061，γ＝8／3时，第一个方程中未加入扰动项和加入扰动项S＝0.00012cos t两种情况下Lorenz系统的相变情况见图5。

由图5可见，系统中加入较小的微弱信号，也不足以使系统的混沌状态发生突变。

3）当参数α＝10，β＝24.0061，γ＝8／3，S＝0.00013cos t＋n（t）时，噪声方差为0.01。受扰Lorenz系统的相变情况见图6。

由图6可见，加入微小的扰动项，系统的相图发生很大变化，系统已经完全进入混沌状态，所以在此情况下，检测的信噪比为：

在Lorenz系统的第一个方程中加入扰动信号，通过实验仿真发现这个加入的微弱信号对系统动力学行为有明显的影响。也可以将扰动项加入其它方程中，同样对系统行为产生显著影响，说明利用Lorenz系统进行微弱光电信号检测是可行的。

4 Rössler系统相图法检测微弱光电信号幅值

对于检测含有噪声的信号，要想检测出信号的幅值，关键的问题依然是系统混沌阈值的确定。设系统参数a＝0.373，c＝10，初始值为˙x，˙y，˙z＝（0，0，0），逐渐调整参数b，仿真结果见图7。

通过大量仿真，发现Rössler系统的混沌阈值大约为b＝18.265，在此情况下，将待检信号S（t）＝Acos（t）＋n（t）加入到第二方程中，其中，噪声方差为0.001，通过大量仿真发现，当待测信号幅值A＝0.00052时，系统依然处于混沌状态，但是稍微增大幅值，如A＝0.00053，系统即由混沌状态进入到周期状态，这个状态的改变是由于在系统中加入了正弦信号引起的，见图8。

因此，系统可检测的信噪比为：

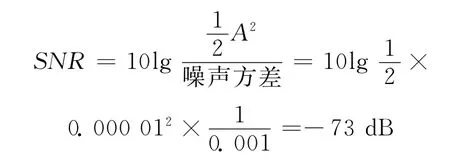
5 相图法检测幅值方法比较

通过上述分析发现，利用典型的混沌振子均能实现微弱光电信号幅值的检测，相比较而言，高阶Lorenz系统和Rössler系统的方程结构更加复杂，因此具有更为复杂的动力学特性。通过观察输入不同信号前后系统相图变化情况，来判断可检测信号的幅值。通过仿真发现，系统参数和初始值对系统状态影响很大，因此，为比较两种方法检测微弱光电信号幅值时的信噪比，针对不同初始状态和参数值，进行仿真，固定Lorenz系统参数α＝10，γ＝28，调节参数β值；而对于Rössler系统，则固定参数a＝0.373，c＝10，调节参数b值。检测结果见表1。

表1 Lorenz系统和Rössler系统检测结果对比表Table1 Measurement result contrast based on Lorenz system and Rössler system

由表1可见，系统初始状态不同，两者的混沌阈值也随之改变，而在相同初始状态情况下，加入相同的噪声方差，可检测的信号幅值有所不同。

比较而言，Rössler系统检测的信噪比更低，更适宜进行微弱光电信号幅值检测，然而，两者利用相图法进行微弱光电信号检测时，无法检测任意大小的微弱信号幅值，具有一定的局限，然而，相对低阶的Duffing系统和VanderPol-Duffing系统而言，这两种混沌振子可检测的信噪比更低，用其进行任意幅值的微弱光电信号检测，理论上来说是可行的，因此仍需继续探讨利用高阶混沌系统检测微弱光电信号幅值的理论和方法。

6 结 论

本文研究了利用新型混沌振子检测微弱光电信号幅值的方法，在重点研究Lorenz混沌振子和Rössler混沌振子动态特性的基础上，使用其进行微弱光电信号幅值检测。检测结果表明，复杂的混沌振子检测微弱光电信号幅值的精度更高，信噪比也较低，为微弱光电信号的幅值检测提供了新思路。

[1]G.Y.Wang，S.He.A quantitative study on detectionand estimation of weak signals by using chaotic duffing oscillators [J].IEEE Transactions on Circuits and Systems-Fundamental Theory and Applications.2003，50（7）：945-953.

[2]庄艳丽.基于混沌振子的微弱信号检测方法研究 [D].成都：电子科技大学硕士学位论文，2006：64-70.

[3]H.K.Simon，X.B.Li.Detection of signals in chaos[J].proceeding of the IEEE.NJ，United States.1999，85（1）：95-122.

[4]S.J.Cang，Z.Q.Chen，W.J.Wu.Circuit implementation and multiform intermittency in a hyper-chaotic model extended from lorenz system [J].Chinese Physics B.2009，18（5）：1792-1800.

[5]Y.Li，B.J.Yang，L.Z.Du，et al.The bifurcation threshold value of the chaos detection system for a weak signal[J].Chinese Physics.2003，12（7）：714-720.

[6]M.Rafikov，J.M.Balthazar.On an optimal control design for Rössler System [J].Physics Letters A，2004，333：241-245.

[7]C.G.Li and G.Chen.Chaos and hyperchaos in the fractional oOrder Rössler Equations [J].Physical A，2004，341：55-61.

[8]张伟伟.基于最大Lyapunov指数的分数阶Rössler系统的混沌现象研究 [D].重庆：重庆大学硕士学位论文，2008：18-37.