混沌蚁群优化的高速公路匝道PI控制器

王 辉，刘智勇，2

（1.五邑大学 信息工程学院，广东 江门 529020；2.江门职业技术学院，广东 江门 529020）

高速公路对出行者有着巨大的吸引力。但大量车辆涌入很容易造成常发性的交通拥挤，同时也可能会导致突发性的交通事故。对高速公路来说，拥挤意味着低效使用，避免或者减少拥挤的发生在高速公路控制中至关重要。入口匝道控制是解决上述问题的有效手段，是应用最为广泛的一种控制策略[1]。其基本目标是在交通流高峰期，调控进入高速公路的车辆数目，使预设性能指标达到最佳，从而保持高速公路交通流运行接近最佳。入口匝道控制实施的前提条件是匝道下游的通行能力大于上游的车流量，入口匝道控制使得高峰时段主线的车速和流量提高，这样不仅缩短了旅行时间，抑制了车流扰动，还减少了交通事故的发生。

文献 [2]用常规的PI控制器实现高速公路的入口匝道控制，控制效果良好，但系统的参数不能在线更新，响应速度较慢。PI控制器简单实用易实现、参数物理意义明确。然而传统的PI控制器参数整定方法是经验试凑人工来选定，这不仅费时而且很难满足控制的要求[3]。针对传统方法的不足，必须寻求智能的参数整定方法，混沌蚁群优化算法为此提供了新的思路。本文结合非线性反馈理论设计了基于混沌蚁群优化算法的匝道PI控制器，采用混沌蚁群算法优化PI控制器参数，并应用到高速公路入口匝道控制中。

1 高速公路交通流模型

图1为一段高速公路，建立交通流数学模型。

图1 一段高速公路Fig.1 A freeway section

其主线的车道数为μ，入口匝道数为1，路段长度为Δx，采样时间为Δt，上游交通流量为qu，下游交通流量为q，主线交通流密度为ρ，平均速度为v，入口匝道调节率为r，路段内车辆总数为N，根据车辆守恒定律可以得到：

定义密度ρ为：ρ（k）＝N（k）／（μΔx），式

（1）两边同时除以μΔx得出：

密度与流量的关系式为：q＝f（ρ），q和ρ有多种表达式，一般有指数型、三角型、抛物线型。非均匀交通流可以采用上述表达式近似描述，它们的共同特性为：①密度为零，流量为零；②存在1个最大密度为阻塞密度，用ρjam表示。当密度达到阻塞密度时，车辆首尾相接流量为零；③存在1个流量最大的临界密度ρc[4]。

格林－希尔兹（Green－shields）提出抛物线型的流量－密度关系如下：

式（3）是由q＝ρv和v＝vf（1－ρ／ρjam）组成的，式中的vf为自由流速度，ρjam为阻塞密度。式（2）和式（3）构成的是一阶模型，它简单易处理适用于交通控制与仿真。

本文采用Green－shields流量－密度关系和公式（3）来描述高速公路交通流，在此基础上建立了反馈控制系统。由式（2）和式（3）可得：

式中δ＝Δt／Δx，ρ（k）为状态变量，r（k）为控制变量，ρ（0）＝ρ0为给定得初始条件，公式（4）完整地描述了高速公路交通流过程。这里上游交通流量qu（k）不受控制的影响，故可以认为是扰动输入。

2 混沌蚁群算法

2.1 混沌优化算法

混沌是在确定性动力系统中出现的一种非线性现象，其行为复杂且类似随机，但也不失内在规律。混沌具有独特的性质：规律性、伪随机性、遍历性和对初始条件的敏感依赖性。混沌优化采用按照其自身运动规律在允许解空间采用混沌变量进行遍历寻优的搜索算法，它易于跳出局部最优并取得满意效果，具有很强的优越性。

描述混沌运动的数学模型很多，典型的混沌系统为Logistic映射[5]。其一维迭代公式如下：

其中，μ 为控制参量，一般μ 取值在 [3.56，4.00]之间，Zi为进行第i次迭代时混沌系统的参量值。随着μ值的变化，在给定Zi的初值后，经过多次迭代将得到一个描述一维质点从有规则到无序运动状态的集合，即混沌状态。混沌状态具有一定的规律性，当μ≥4时，产生的不动点数增多。有序运动进入混沌状态。当μ＝4，0≤Z0≤1，Logistic完全处于混沌状态，可得到：

其中，i值越大，获得Zi＋1的值就越大。所以初始值相近的随机数能够得到完全不同的随机数序列，这是混沌映射的性质。

2.2 蚁群算法

蚁群算法是一种随机搜索的仿生进化算法，通过候选解组成群体的进化过程来寻求最优解[6]。蚂蚁个体之间的交流是通过信息素进行信息传递的，在运动过程中，蚂蚁能够在它所经过的路径中留下信息素，以感知信息素的浓度来此指导自己的行动，移动一般倾向于选择信息素浓度高的方向。

蚁群算法寻优的关键是点与点之间的转移概率以及路径上的信息素浓度。假设在寻优初始时刻，各路径上的的信息素浓度相等且为C，即τij（0）＝C（C为常数）。蚂蚁k（k＝1，2，…，m）在运动过程中，根据各路径上的信息量决定其转移方向，用（t）表示蚂蚁k在t时刻由当前节点i移至节点j之间连接概率：

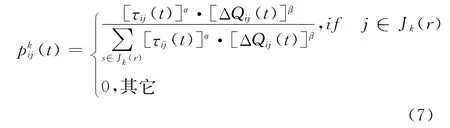
其中Jk（r）表示蚂蚁k下一步允许访问的节点；ΔQij（t）为启发式因子，表示蚂蚁从节点i移至节点j的期望程度，一般取ηij＝1／dij，dij为节点之间的距离；α为轨迹的重要程度（一般建议α≥1）；β表示能见度的重要程度（一般建议β≥0）。经过n个时刻，蚂蚁走完所有的节点，完成了一次循环。此时，要根据式（8）对各路径上信息素重新调整：

其中，ρi∈（0，1），它表示轨迹上信息素的蒸发系数，1－ρi理解为信息量的保留系数。信息素增量Δτij表示为

其中，Q为常数；Ck表示第k只蚂蚁本次循环所走过的路径长度；Δτij表示循环一周路径i j上信息素的增量。

2.3 混沌蚁群算法

为了解决蚁群算法在应用中出现的停滞和扩散问题，在其中嵌入混沌优化的思想。在蚁群初始化时，采用混沌遍历性进行混沌初始化，每个混沌变量对应一条路径，所以能够产生大量的路径，选择其中较优的路径并留下信息素，所有路径初始信息量各不相同，在此基础上蚂蚁再选择路径[7]。同时在信息素更新方程中引入混沌扰量，避免蚁群算法陷入局部最优。对此，公式（8）修改为：

其中，Zij为混沌变量，由公式（5）得到，η为系数。

混沌蚁群算法步骤如下：

step 1：混沌初始化，令循环步数λ＝0。由式（6）非线性Logistic映射可得到初始τij，调整各路径的信息素，将m个蚂蚁放置在n个顶点上，设置Q，τij，Δτij，η，Zi的初始值。

step 2：将各蚂蚁的初始出发点置于当前解集中，对每个蚂蚁k（k＝1，2，…，m），按概率移至下一顶点j，将顶点j置于当前解集。

step 3：计算并记录各蚂蚁的路径长度Ck（k＝1，2，…，m），若优于此时的最优蚂蚁，则替代为全局最优。

step 4：对全局最优蚂蚁，按式（11）更新信息素，按式（7）更新转移概率。

step 5：令λ＝λ＋1。

step 6：若λ＜预定的迭代次数且无退化行为（即找到的都是相同解）则转到步骤2。

step 7：输出当前最优解，完成寻优过程。

3 基于混沌蚁群优化的入口匝道PI控制器

基于混沌蚁群优化的入口匝道PI控制器见图2。传统PI控制器参数Ki、Kp的整定方法是依靠人工经验试凑的方法选定的，此方法要求操作熟练，同时还需大量的时间。此外，这种传统PI控制器缺乏自适应能力，当交通流模型受到干扰而发生变化时，PI控制器不能作出相对应调整，而只能采用人工经验试凑重做参数整定。鉴于蚁群优化算法是通过个体间的协作来寻找最优解，能够简单、高效的解决实际工程问题。在此基础上通过引入混沌算子改善全局收敛能力，构造模式搜索方法提高局部最优解搜索能力，形成了混沌蚁群算法。结合非线性反馈理论，用PI控制器实现匝道控制，用混沌蚁群算法寻找最佳PI参数。图2用混沌蚁群优化算法选择和优化PI控制器的参数Ki、Kp，以获取最优解。

图2 基于混沌蚁群优化的入口匝道PI控制器Fig.2 Ramp PI controller based on CACO

图2中，误差为：e（k）＝ρd（k）－ρ（k），误差变化为：Δe（k）＝e（k）－e（k－1），PI控制器的输出为：Δr（k）＝KpΔe（k）＋Kie（k），入口匝道的调节率为：r（k）＝r（k－1）＋Δr（k），式（4）描述了交通流的模型。图2所示的是一个非线性闭环反馈系统，期望的交通密度ρd为系统输入，上游流量qu为扰动输入，实际的交通密度ρ为系统的输出，控制变量为入口匝道调节率r，交通密度ρ的控制作用是通过调控进入高速公路的交通流量来实现。PI控制器通过调控入口匝道的调节率r能够使输出的实际交通密度ρ跟踪输入的期望交通密度ρd。此闭环反馈控制可以有效抑制扰动输入qu的噪声和交通流模型误差。该系统的响应速度快、鲁棒性强，稳态误差接近于零。

4 仿真研究

在仿真过程中为了比较，本文还用蚁群算法对高速公路匝道PI控制器的参数进行了优化。CACO与ACO优化的最佳PI参数比较见表1，目标函数值J的变化曲线对比见图8。可以看出在高速公路入口PI控制器参数优化过程中，混沌蚁群算法比蚁群算法更加优越。

上游流量qu变化曲线见图3，实际密度ρ变化曲线见图5，入口匝道调节率r变化曲线见图7。从仿真结果图3和图7得出，初始时入口匝道调节率r随时间增长，这是由于初始的上游流量qu保持不变，实际交通密度ρ从初始密度增长到34.20辆／km／车道，直到最后几乎不变。入口匝道调节率r随上游流量qu的波动而波动，当qu增加时，调解率r减少；qu减少时，r增加；qu不变时，r也不变。上述变化规律完全符合实际匝道的控制规律。由图4和图5可见，实际的交通密度能够很好地跟踪期望的交通密度，稳态时的实际密度与设定的期望密度几乎完全相同，说明基于混沌蚁群优化的高速公路入口匝道PI控制器具有良好的动态和稳态性能。

从图5和图6对比可以看出本文方法明显优于文献 [2]。首先缩小了期望密度ρd与实际密度ρ间的误差，提高了稳态精度；其次混沌蚁群优化算法可以迅速地搜索到Ki和Kp的优化值，有效的克服了复杂费时的人工整定参数的过程。

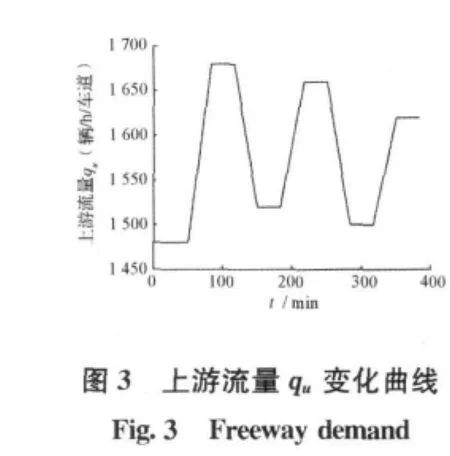
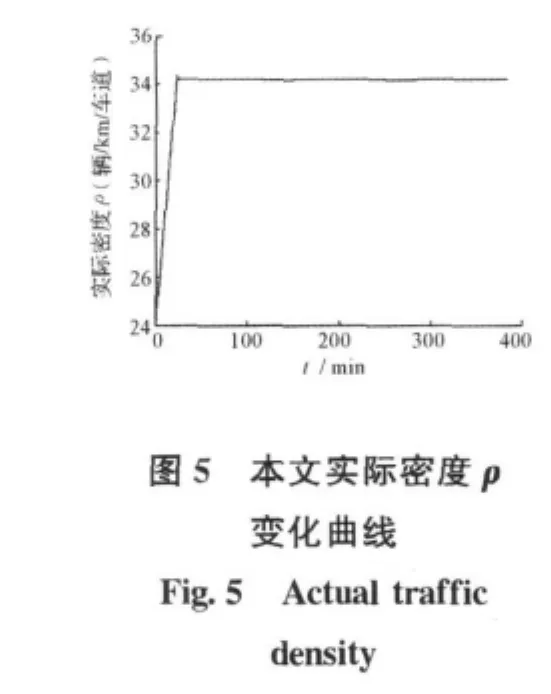
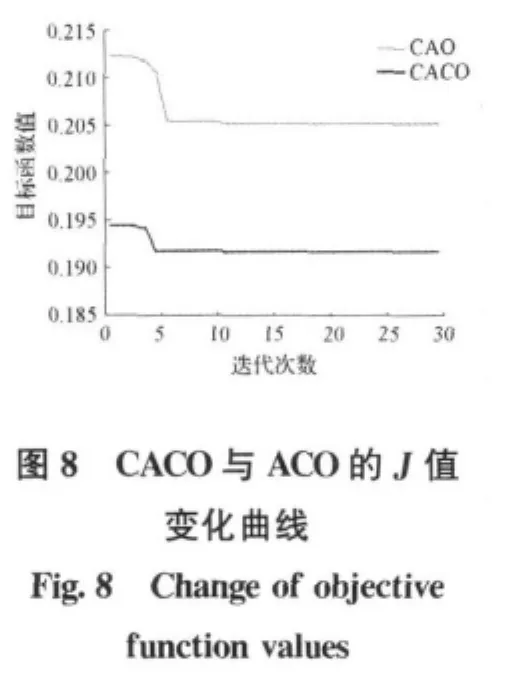
表1 CACO与ACO仿真结果对比Table1 CACO and ACO simulation results comparison

5 结 论

高速公路入口匝道控制是一种有效的交通控制手段。本文结合非线性反馈理论，设计了高速公路入口匝道PI控制器，并利用混沌蚁群优化算法优化控制器参数。该控制系统有效的克服了复杂费时的人工整定参数的过程，又有常用PI控制器简单实用易实现、参数物理意义明确的优点。仿真结果表明，该系统响应速度快，鲁棒性强，动态和稳态特性良好。混沌蚁群算法有效避免搜索过程陷入局部最优，弥补蚁群算法的不足，提高解的多样性和全局寻优能力。将混沌蚁群算法应用到高速公路入口匝道PI控制器的参数整定中，取得了良好的控制效果，相对于传统的用人工经验试凑法和蚁群算法整定PI控制器参数，本文的方法具有明显的优越性。

[1]刘智勇.智能交通控制理论及其应用 [M].北京：科学出版社，2003.

[2]梁新荣，刘智勇，毛宗源.高速公路匝道非线性反馈控制器的设计与仿真 [J].计算机工程与应用，2005，41（20）：111-113.

[3]李 政，梁新荣.基于遗传算法优化的高速公路匝道PI控制器 [J].计算机工程与应用，2008，44（4）：216-218.

[4]X.R.Liang，Z.Li.Freeway ramp control based on genetic PI and fuzzy logic[J].Proc.of the Pacific－A-sia Workshop on Computational Intelligence and Industrial Applications，Wuhan，China，Dec，2008：382-387.

[5]WEI Gong，Shoubin Wang.Chaos Ant Colony Optimization and Application [C].4th International Conference on Internet Computing for Science and Engineering，2009：301-303.

[6]段海滨.蚁群算法原理及其应用 [M].北京：科学出版社，2005.

[7]杨 海，王洪国，侯鲁男，等.混沌蚁群算法及其在智能交通中的应用 [J].成都大学学报：自然科学版，2007，26（4）：309-312.