复式行星齿轮传动装置的自由振动特性(一)

1 前言

目前太多数汽车自动变速器多采用两排单列行星齿轮、单级行星齿轮装置排列实现的5档和6档的变速器。然而“复式”行星齿轮传动已成为应用大功率自动变速器最普通的布置方式。它们的多列星齿轮的设计,与通常的中间轴齿轮传动相比,有可能造成大的转矩重量比。

复式行星齿轮传动装置(CPGT)用于很多实际如汽车、航空和重型工业,这是由于它们具有特别大的紧凑性,大的转矩重量比和低的轴承负荷。同样CPGT的输入和输出的联接只要经过简单的改变,就能获得不同的速度和转矩比,不变更其部件就能得到十分期待的自动变速器。Gott[1]采用两个单列星齿轮单级行星齿轮传动获得了或4个前进速比。采用CPGT增加机构效率在大功率自动变速器中已成为十分普遍[2]。

CPGT的两个最普通的实例是采用二和三个行星齿轮如图1所示。图1(a)示第一部件是大家熟知的Rarigneaux'齿轮装置[3,4],一个长的行星齿轮连接了双行星齿轮装置 S1-a-b-r2和S2-d-a-r1(S1和S2是太阳轮,r1和r2是齿圈以及b和d是短行星齿轮)的两平面,所有行星齿轮由单行星架c支承。在该示意图中,可60功率流布置。图1(b)示第二种CPGT,本文提出一种不同的方案图是只选用两单行星齿轮传动,所以S1-a-r1和S1-a-b-r2是通过长行星齿轮a和短行星齿轮b彼此相互连接。在确定的元件布置中,它可以获得相同的传动比和输入-输出元件,可以找到-24功率流布置。

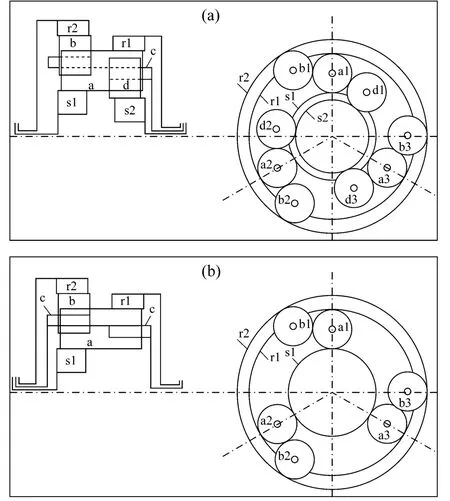
图1 两常用的CPGT：(a)‘Rarigneaux'齿轮装置和(b)简化的‘Rarigneaux'齿轮装置Fig.1 The twomostused CPGT ：(a)‘Rarigneaux'gearset and(b)Simplified‘Rarigneaux'gearset

另一方面,如任何齿轮变速装置,在噪声和振动方面,是CPGT应用中一个大问题,它导致研究者们[5-7]为了确保安全和舒适性而集中于其控制。如果设计者们可计算和分析自由振动特性以便避免装置运转时接近临界工作速度,那么变速器的齿轮噪声和振动问题可以降低,这也是本研究的目标之一。在文献[8-13]中已广泛进行单级行星齿轮传动振动的模拟。在Lin和Parker[4,14,15]的单级直齿轮行星齿轮传动的研究中,求得三种类型的模式：移动、转动和行星齿轮模式。

为模拟行星齿轮传动,Howells[16]、ABousleiman和Velex[17]以及Parker等[18]采用多自由度的有限元模型,它导致多的计算时间,该CPGT包含比单级行星齿轮传动更多的部件,采用有限元方法使问题更加复杂,求解更加困难。而在文献中找出不用有限元模型的CPGT。为此,本研究的主要目标是开发每个部件具有三个自由度的CPGT的简单概括性参数动力学模型,它考虑了齿轮和轴承的变形,并导出CPGT的主要振动特性。对数目不同的行星齿轮找出和分类该CPGT的主要振动特性。对数目不同的行星齿轮找出和分类该CPGT的固有振动模式,研究这些行星齿轮的陀螺效应和几何位移的影响。该CPGT的典型特征最重要的是其动力响应的预测。

2 动力学模型

2.1 CPGT的平面模型

研究每个部件具有三个自由度的CPGT平面振动问题(图1(b))采用的模型如图2所示,假定太阳轮(S)、齿圈 1(r1)、齿圈 2(r2)、行星架(c)、N 行星齿轮a和N行星齿轮b分别是具有转动惯量为Js、Jr、Jr2、Jc、Ja和Jb和质量为mr1、mr2、mc及mb的刚体,用 ui,vi和θi,i=c,r1,r2,s,la,…,Na,lb,…,Nb表示行星架、齿圈1、齿圈2、太阳轮和行星齿轮的移动和转动 ,测量这些基架(0,s→,t→,z→)固定行星架并以常用速度 Ωc转动的座标,用相应移动齿轮啮合位移代替转角 θi,如 ：ρiz=Rbiθi(Rbi是太阳轮齿圈1,齿圈2行星齿轮ia,行星齿轮ib和行星架的基圆半径,i=1,…,N),位移矢量qi确定为qi=[ui,vi,ρiz]T,i=c,r1,r2,s,la,… ,Na,lb,… ,Nb。行星齿轮ia和行星齿轮ib(i=1,…,N)位置用固定角度αia和αib详细规定,它是相对转动基础矢量测量 ,以致 α1a=0°和 α1b=0°。

图2 研究CPGT的平面模型Fig.2 A Plane model of the Studied CPGT

2.2 行星齿轮模拟

行星齿轮ia和行星齿轮ib轴承的相对径向和切向位移 ΔiaR,ΔibR和 ΔiaT和 ΔibT表示为[10]

对于太阳轮a,行星齿轮a-行星齿轮b,行星齿轮a-齿圈1和行星齿轮b-齿圈2为[10]

表1和表2分别列出式(1)和(2)内给出的系数表达式。

表1 公式(1)内系数表达式Table 1 Expressions for the coefficients given in equation(1)

表2 公式(2)内给出系数表达式。α为压力角和αab如图2所示Table 2 Expressions for the coefficients given in equation(2);αis the pressure angle and αabis shown in Fig.2

2.3 轴承模拟

轴承用常刚度kix,kiy,i=c,r1,r2,s的线性弹簧来模拟。所有行星齿轮的轴承刚度假定等于固定值kxx和kyy。所有太阳轮一行星齿轮a,行星齿轮a-行星齿轮b,行星齿轮a-齿圈1和行星齿轮b-齿圈2的轮齿啮合用随时间变化刚度ksi(t),kabi(t),kr1i(t),kr2i(t),i=1,…,N的线性弹簧模拟,在模拟中不提到阻尼,不过,它可在齿轮啮合和轴承刚度对比中介绍。

3 CPGT运动方程式

由Lagrange公式导出CPGT各部件的各个别运动方程式,再综合为一矩阵形式求得系统的普遍公式

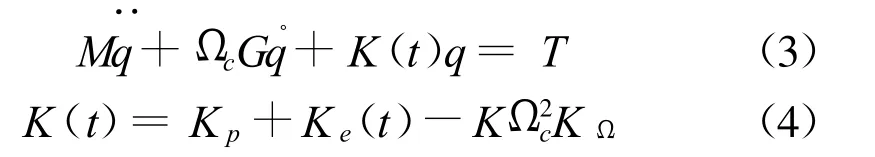
式中g为位移矢量,T为外转矩矢量,M为质量矩阵,G为陀螺矩阵,Kp为轴承刚度矩阵,KΩ为向心刚度矩阵和随时间变化刚度矩阵为Ke(t)。关于公式的开发由附录(3)给出。

该随时间变化啮合刚度矩阵可写成

式中Kv(t)为时间变化刚度矩阵,K0为名义刚度矩阵。

对于行星架小的转动速度,陀螺G和KΩ可以忽略,而固有值问题与式(3)联合为

对于行星架高的转动速度,不能忽略系统的陀螺效应对动力学特性的影响,固有值问题成为

式中 ωi为固有频率,φi为相应的振动模。

采用状态空间可以解式(7),系统公式的规模将为6N+12

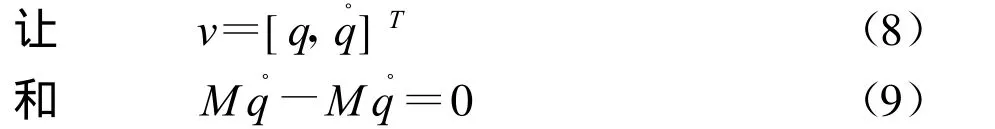
联立所有(3)式和(7)～(9)式得

它可以写成

式中

该新问题和固有值问题将如下

由找出矩阵L-1R的固有值可以得到系统的固有频率。

为证明所有这些影响,用一系列的仿真可以实现为了研究行星齿轮的位置和数目以及陀螺效应对CPGT动特性的影响。假定行星齿轮是相同和相等空间,采用这样的规格,该CPGT将具有环状对称结构,它导致不同的固有频率和振动模式特性。具有固定齿圈2的-CPGT的数值实例列于表3。该刚度值取自文献[10],固有频率计算列于表4。

4 数值结果

和普通中间轴齿轮传动装置相比较,增加CPGT行星齿轮的数目可增大转矩质量比。因此其啮合数增大(图3),其结果考虑齿轮啮合刚度更复杂,如于对CPGT的激励源和造成系统内更大的振动。另一方面,为获得一精确的CPGT,改变第二排行星齿轮的位置可以造成并确定系统的动力特性。对应用于高速,陀螺效应的研究是很重要的,因它此时不可忽略。

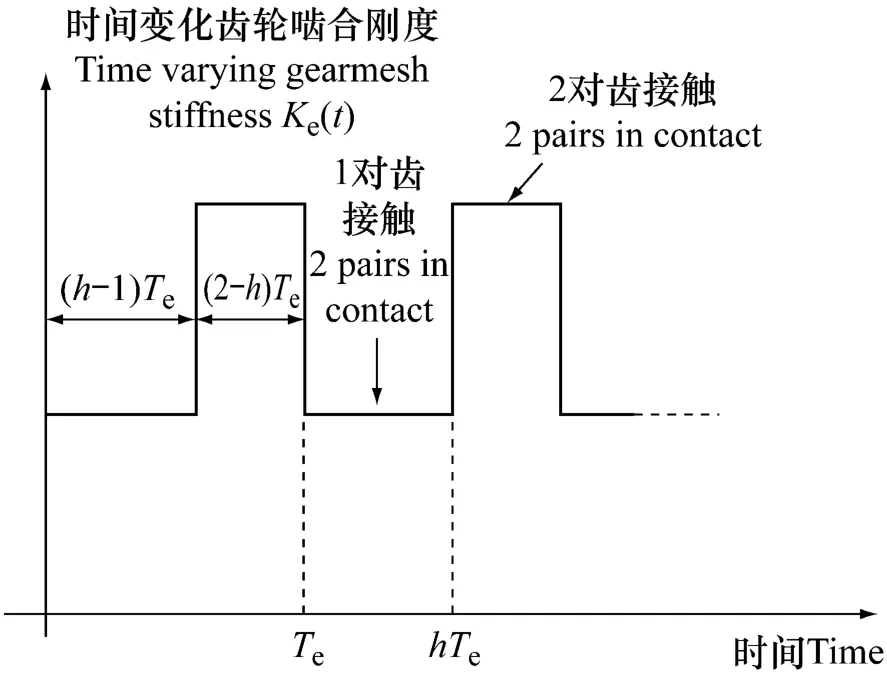
图3 时间变化齿轮啮合刚度计算结果Fig.3 Time varying gearmesh stiffness computation

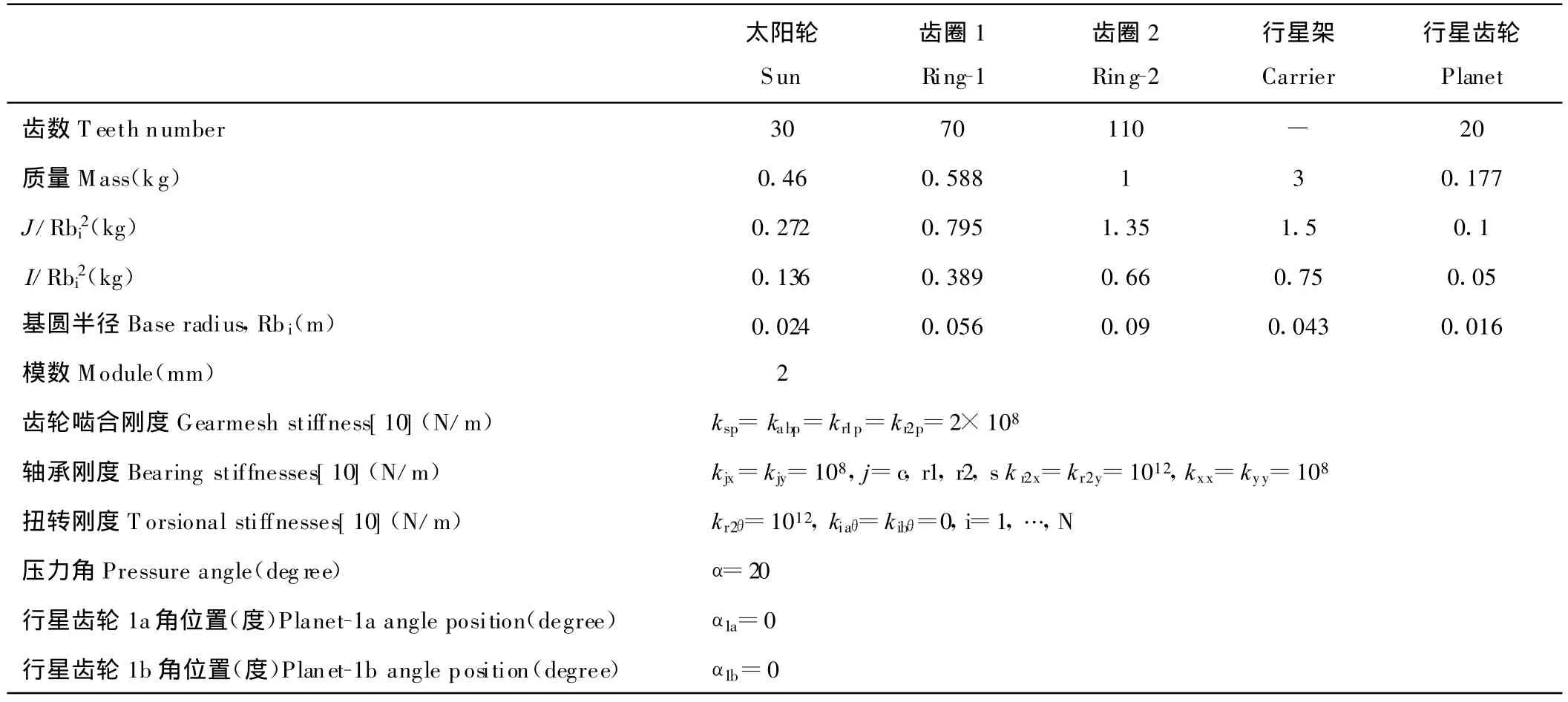
表3 复式行星齿轮传动模型参数Table 3 Parameters of the compound planetary gear train model

仔细观察固有频率Fi(i=1,…,N)和模式形态揭示几种特性,对不同的行星齿轮N找出典型的振动模式：

1.移动模式：行星架,齿圈1和太阳轮有纯最常见的移动没有转动的变形(ui≠0,vi≠0,ρi=0,i=s,c和r1)。

2.转动模式：行星架,齿圈1和太阳轮具有纯最常见的转动没有移动(ui=0,vi=0,ρi≠0,i=s,c和r1)。

3.行星齿轮模式：只有行星齿轮有一最常见的变形。

4.1 每排具有一个行星齿轮的CPGT N=1

根据表4表示的结果,它可包含的所有固有频率是不同的,该值得注意的模式是这些刚体(F1=0 Hz)齿圈1(F6=2075 Hz)移动模式,齿圈2(F16=159160 Hz,F17=159190 Hz)移动模式,太阳轮(F8=2346 Hz)移动模式和齿圈2(F18=167800 Hz)的转动模式。齿圈2运动发生在高频,因为它是固定的。

表4 研究CPGT的固有频率：刚体模式(RBM)移动模式(T),转动模式(R),行星齿轮模式(P),双模式(D),和三模式(Tr)Table 4 Natural frequencies of the studied CPGT：rigid body mode(RBM),translational mode(T),rotational mode(R),planet mode(P),double mode(D),and triple mode(Tr)

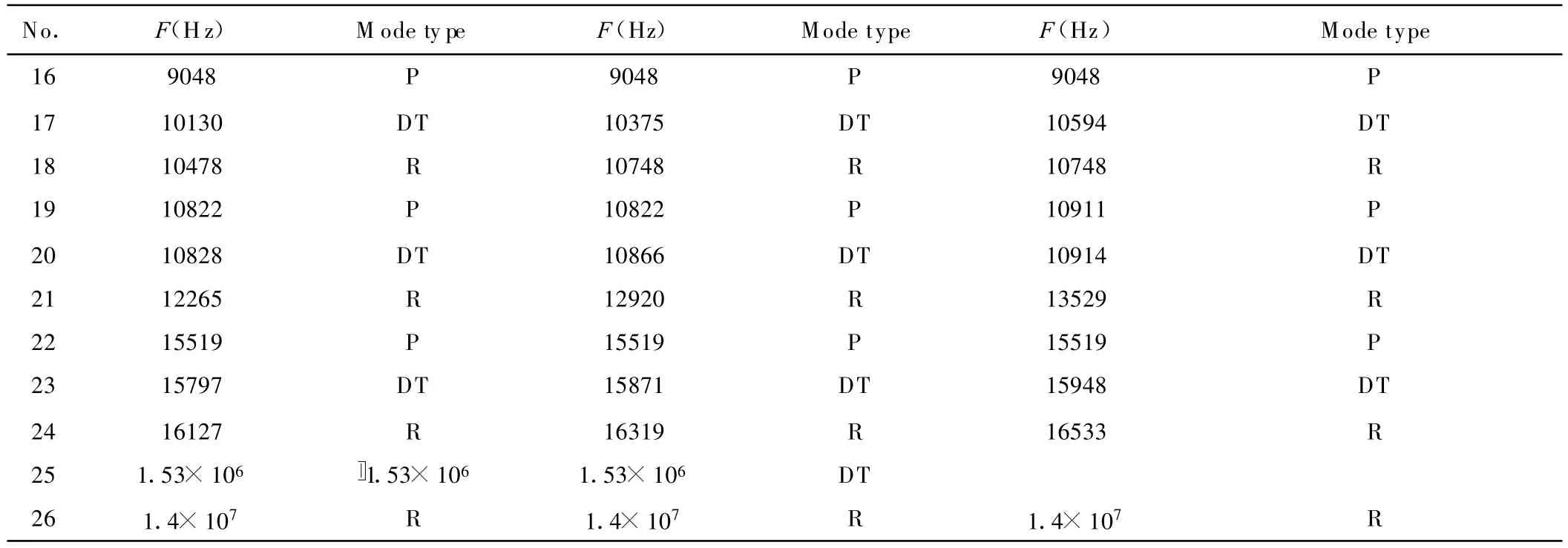
续表4

4.2 每排具有2个行星齿轮的CPGT：N=2

在这种情况,固有频率是不同的,对于N=1求得频率(0,2075,2346,159160,159190和167800 Hz)保持不变。此外,找到两种模式,关于最常见的移动模式,第一级含太阳轮,行星架和齿圈,固有频率具有一个最常见的移动运动,相对的行星齿轮是具有相同运动相位相反(图4)。第二级含固有频率为太阳轮,行星架,和齿圈1具有最常见的转动运动,相对的行星齿轮是同相位具有相同运动(图5)。

图4 对于移动模式的模式形态F3：相对行星齿轮相反相位Fig.4 Mode shapes for translational mode F3：the opposite planets are counter-phased

图5 对于转动模式的模式形态F4：相对行星齿轮同相位Fig.5 Mode shapes for rotational mode F4：the opposite planets are in-phase

4.3 每排有三个行星轮的CPGT：N=3

在这种情况,振动模式分为二类：移动和转动模式(表4)。第一级含10个重复的固有频率为太阳轮,行星架,和齿圈1有一移动运动。行星齿轮是相反相位布置,它们的移动量总和等于零。第一对行星齿轮(a,b)的运动补偿了其他行星齿轮的运动(图6)。第二级含10个不同的固有频率为太阳轮行星架和齿圈1有一转动,各行星齿轮为同相位,具有相同的运动(图7)。Hbaieb等[10]也发现了相同的分类。

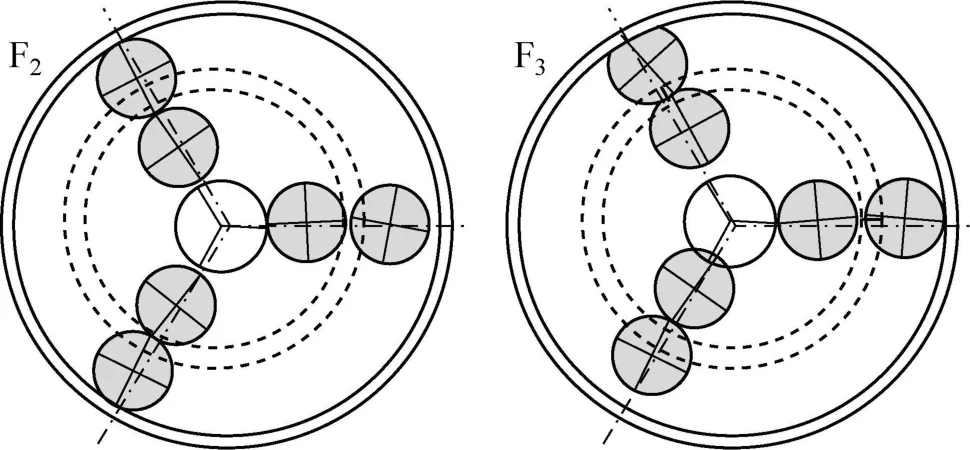
图6 转动模式的模式形态 F2和F3：相对行星齿轮相反相位Fig.6 Mode Shapes for translational modes F2and F3：the opposite planets are counter-phased

图7 转动模式的模式形态F4：相对行星齿轮同相位Fig.7 Mode Shapes for rotational mode F4：the opposite planets are in-phase