基于CG-MSNWF的空时自适应抗干扰算法研究*

潘延明，卢艳娥，骆艳卜，李思佳

(空军工程大学 电信工程学院，陕西 西安710077)

空时自适应滤波算法的优点是能够在不增加天线阵元数目的前提下大大提高信号处理的自由度，并可以抵消诸如连续波干扰、调频干扰等多种窄带和宽带干扰。在最小均方误差MMSE(Minimum Mean Square Error)准则下，维纳滤波WF(Wiener Filter)对期望信号的估计是最优的[1,2]。维纳滤波仅仅依赖观测信号的二阶统计量，易于实现，因此被广泛应用于多种场合。但是该方法需要计算观测信号的自相关矩阵的逆矩阵，这意味着空时自适应滤波的计算量会随着自相关矩阵维数的增加而急剧增大。因此，在当前硬件条件下，以降低计算量为目的的降秩处理是空时自适应滤波所研究的重要问题之一[3]。

针对空时自适应滤波问题，现有的降秩方法很多，其中应用最广泛的是多级维纳滤波MSNWF。相对于其他的降秩方法，MSNWF有更优的稳态和瞬态性能，能够在处理器维数远小于信号空间维数时，使性能接近最佳，并且避免了求解矩阵的逆、特征空间分解等复杂的运算，给计算带来了方便[4-5]。然而，MSNWF包含前向迭代和后向迭代两个过程，在阵元数目过多时，双向迭代过程使MSNWF的计算量大大增加，难以满足实时性的要求。针对这一问题，本文采用基于共轭梯度的多级维纳滤波算法CG-MSNWF,该算法只有前向迭代过程，避免了开放运算，计算量小。在相同的干扰抑制性能条件下，该算法的收敛速度比MSNWF有所提高，能够快速适应时变的场景，易于实时处理。

1 MSNWF算法

设阵列的阵元数为M,每个阵元含有P个延迟单元。信号经过M个天线阵列进入系统，数据采取分段输入方式，数据段长度为L。这样，每次处理的数据量为M×L维，数据经过延迟处理后转换为N×(LP+1)维矩阵(MP=N),用X表示。处理器权向量为W，接收数据的自相关矩阵为RX=E[XXT],观测信号与期望信号的互相关为rxd=E[Xd*]。

选择满秩矩阵T1=[h1]T作为预滤波,其中h1=/‖‖，B1=null(h1)称为阻塞矩阵(Blocking Array)。

设对输入信号X0(n)进行T1变换之后得到的信号为Z1,则：

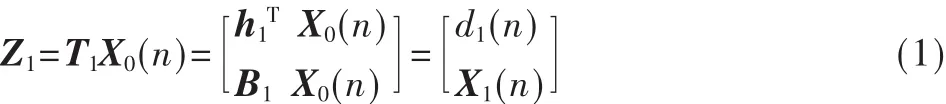
用观测信号向量X0(n)满秩变换后的Z1(n)来估计期望信号d0(n)，由维纳滤波器的时域解可知：

由此可以看出，N维维纳权可以分解为一个标量与一个(N-1)维维纳权的形式，即:

其中, 标量 w1=δ1，(N-1) 维矢量为从(N-1)维矢量X1中估计标量d1的维纳权。

同理，继续将 X1(n)分解，直到分解到第(N-1)级，如图1所示。这时，XN-1(n)已经是一个标量，维数等于 1。维的维纳滤波器被分解为N个级联的标量滤波器。由式w1=α1-1δ1可知，每级标量维纳滤波器的权值可由两个标量相乘得到。

图1表明了MSWNF降秩算法需要有前向迭代和后向迭代两个过程，前者的作用通过将输入信号变换到相互正交的子空间进行降秩,后者的作用是用各级的误差信号加权来估计期望信号[6-8]。估计的误差为：

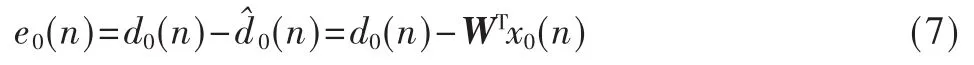
则估计的均方误差MSE为：

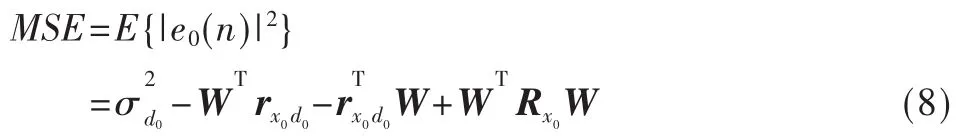
2 MSNWF改进算法

在MSNWF算法中,需要估计观测信号的自相关矩阵，迭代的最大维数为N-1,在每次迭代时观察最小均方误差 αi，当迭代至 D(1≤D≤N-1)时，αi小于预先设定的MMSE门限，迭代即终止[7]。但是在迭代过程中需要反复进行开方运算,不利于硬件实现。J.Scott Goldstein等人针对 EDGE(Enhanced Data rate for GSM Evolution)系统提出一种基于共轭梯度的多级维那滤波算法CGMSNW[9],本文将该滤波算法应用于GPS接收机前端，仿真分析表明，具有很好的抗干扰效果。

2.1 共轭梯度（CG）算法

共轭梯度(CG)算法是Hestenes和 Stiefel在求解 N(N未知)阶线性方程组Ax=b时所提出的[9]。求解过程是一个步迭代过程，当第D次迭代之后输出的最小均方误差αi小于预先设定的MMSE门限值时，迭代可以终止，此时的解向量xD是方程组的近似解。

共轭梯度算法是以下问题的解：

称为权重因子，pi称为导向矢量，xN是第N次迭代之后的近似解向量。

设解向量x的迭代方程为：

现在估计γi的值，使误差函数f(x)取得最小，可得：

第i-1次迭代之后的剩余误差为：

将式(12)代入式(14)可得：

2.2 基于CG的MSNWF算法

关于MSNWF和CG算法的分析比较，参考文献[9，10]给出了详细的论述。下面直接给出CG-MSNWF的算法流程：

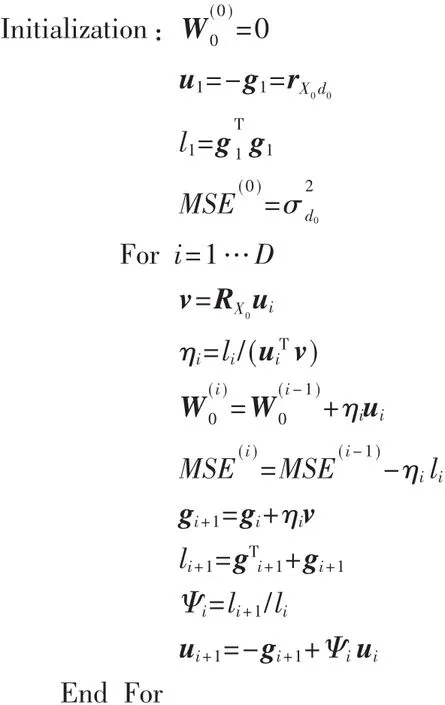
比较CG-MSNWF和MSNWF两种算法可以发现，前者不仅实现简单，而且在迭代运算中避免了开方运算，既不需要后向迭代，也不需要计算阻塞矩阵B,从而简化了运算过程，提高了运算效率。因此，本文采用CGMSNWF算法作为求解维纳滤波器权系数的方法。

3 仿真分析

为了充分验证CG-MSNWF算法的有效性和可靠性，本文对算法的干扰抵消和收敛情况进行了仿真。

3.1 CG-MSNWF对干扰抵消情况

采用阵元数为M=7的均匀线性天线阵，每个天线阵的延迟为P=4。接收机处理带宽B=20 MHz，中频 IF=46.52 MHz，采样率 FS=65.536 MHz。GPS信号的信噪比S/N=-15 dB，DOA为 30°，设 PRN码偏移量为 0。设干扰个数为10个，如表1所示。

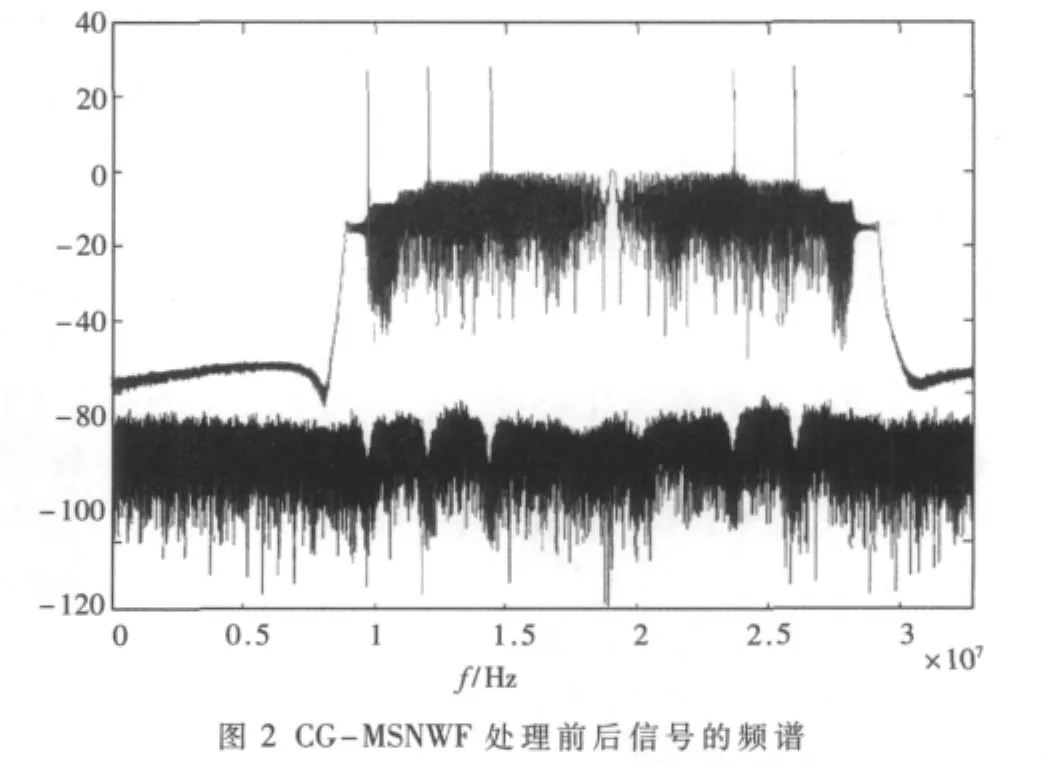
采用CG-MSNWF处理前后的信号频谱图如图2所示。经过CG-MSNWF算法的输出信号中干扰成分已被有效抑制，在输出信号的频谱中，单频干扰和宽带干扰均被抵消掉，其中在单频干扰信号的频点处产生凹陷，凹陷的幅度约为10 dB，达到了抗干扰的目的。

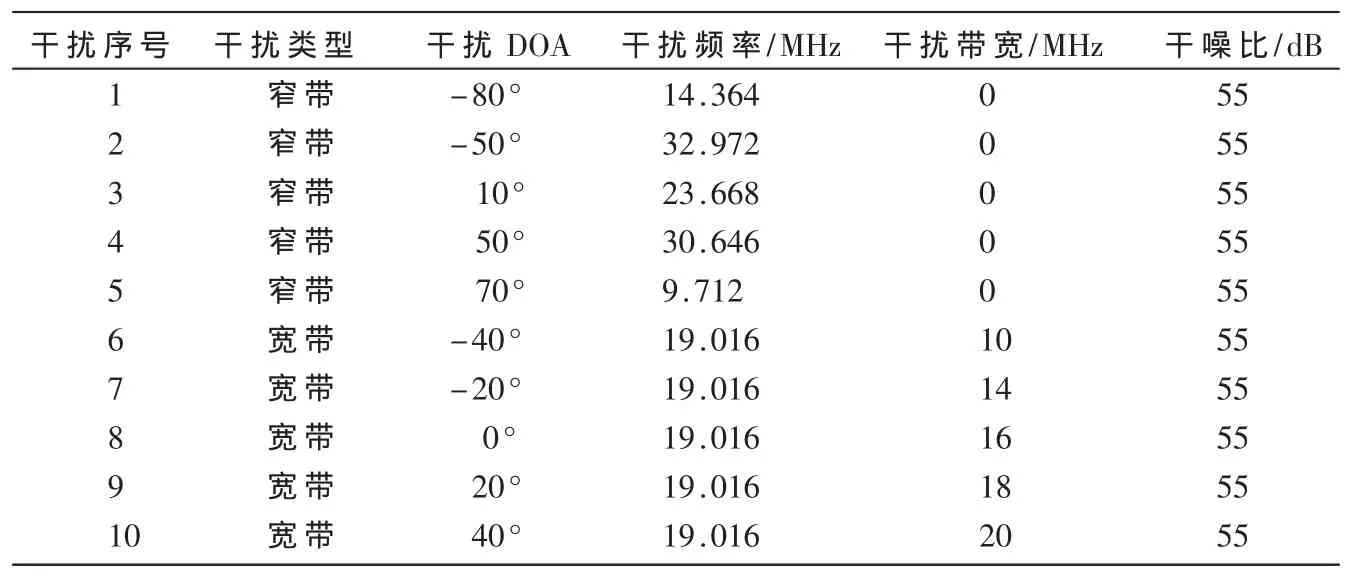
表1 干扰信号信息表

在实际应用中，用PRN自相关的最大峰值与次大峰值的比值[11]来检验算法对干扰的抵消情况，判断是否可以检测到GPS信号，其经验判决门限为最大峰值与次大峰值之比等于1.5 dB。在本次仿真试验中，根据图3所示，该比值为4.57 dB，所以经过CG-MSNWF算法处理之后,可以检测到GPS信号,从而证明了算法的有效性。

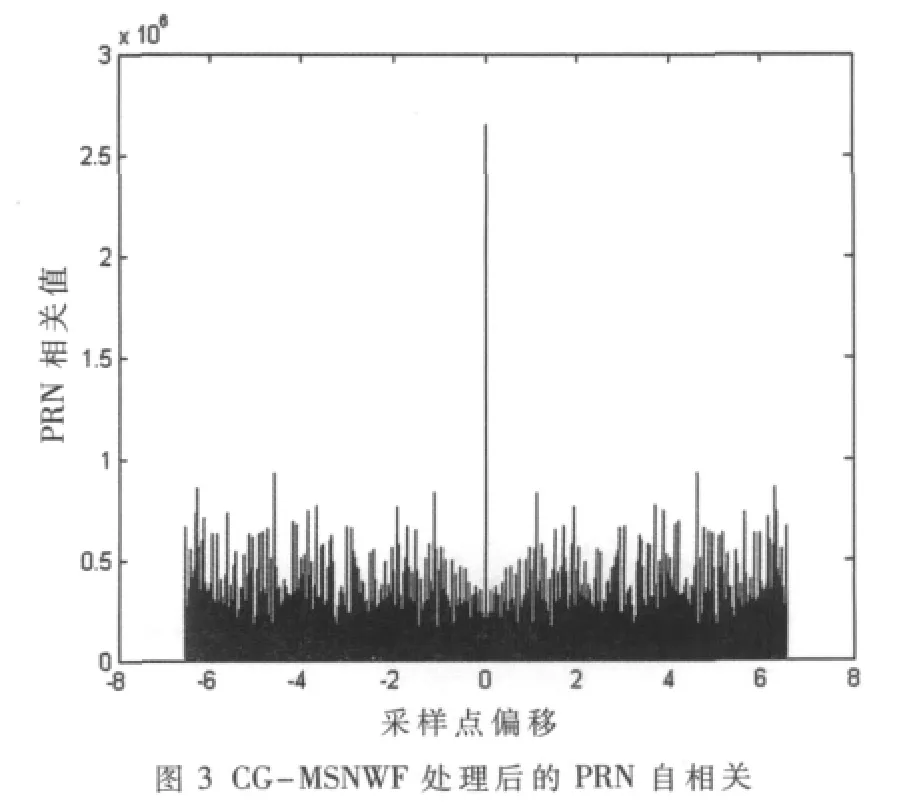
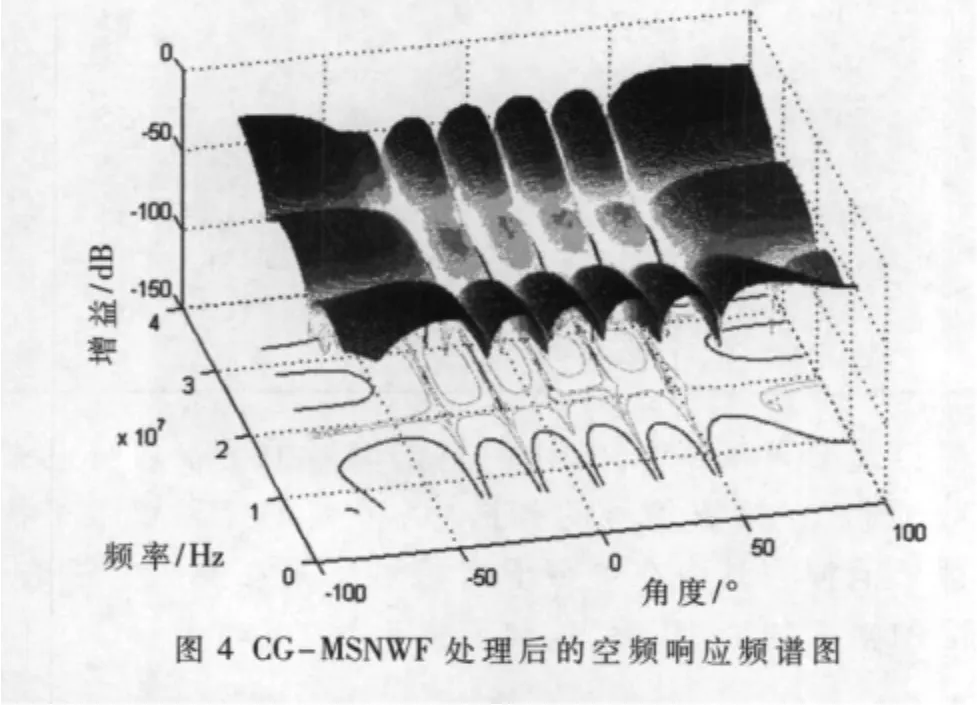
图4为滤波输出信号的空频响应，可见在与表1所对应的干扰DOA和干扰频率(频带)处产生凹陷，进一步证明了该算法对干扰抵消的效果是非常理想的。

3.2 CG-MSNWF的降秩和收敛性能

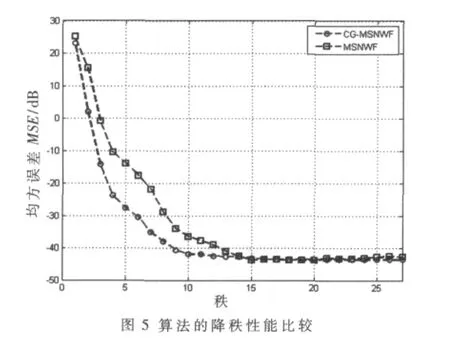
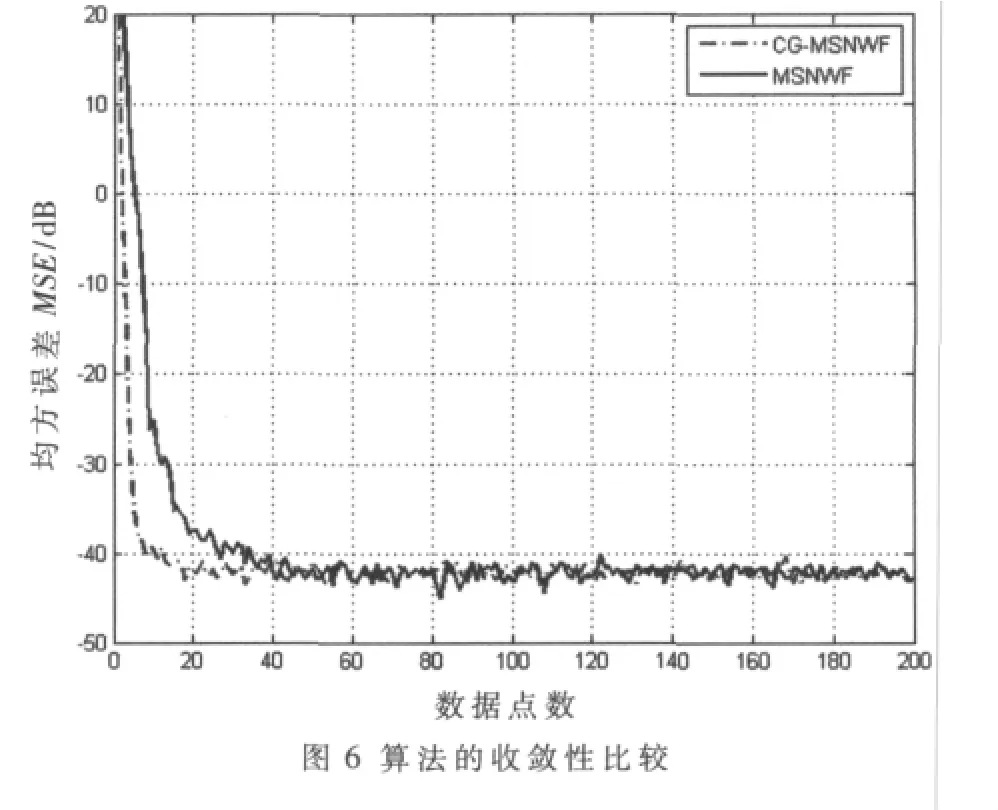
对MSNWF算法的研究表明,MSNWF是一种降秩自适应滤波方法，该算法使系统在秩远小于信号子空间秩的时候趋于收敛[4,5]。CG-MSNWF是MSNWF基于共轭梯度的改进算法，也是一种降秩自适应滤波方法。CGMSNWF算法不需要后项迭代过程，运算简单，降秩性能好，从而大大降低了计算量，提高了收敛速度。图5和图6分别给出了两种算法降秩性能和收敛性能比较。可以看出，CG-MSNWF算法在系统的秩R=10时就趋于收敛，降秩性能优于MSNWF算法；系统达到稳态的秩减小了，说明算法的计算量有所减小，实时性有所增加，能够快速适应时变的场景。

本文针对MSNWF算法计算量大，在处理高维数据时，不能满足实时性要求这一问题，采用基于共轭梯度的改进算法——CG-MSNWF，该算法是一种降秩自适应算法，省略了后项迭代过程，计算简单，可以使系统在秩R=10的时候就趋于收敛，且性能与满秩时相差不大，从而克服了其他空时自适应滤波算法的计算量大的弱点，增强了抗干扰的实时性。本文对该算法的有效性和可靠性进行了仿真,仿真结果证明了该算法的合理性。

[1]卢艳娥.“北斗一号”用户接收机自适应抗干扰天线半物理仿真系统关键技术研究[D].北京：北京航空航天大学博士学位论文，2004.

[2]高增来,卢艳娥.空时自适应抗干扰算法分析与仿真[J].通信技术，2007，40(12)：174-176.

[3] 卢艳娥，谈展中.用于双卫星导航系统用户接收机抗干扰的自适应干扰正交约束下的最佳信号增强算法[J].电子学报，2004，32(8)：1239-1243.

[4]GOLDSTEIN S J,REED I S.Reduced-rank adaptive filtering[J].IEEE Transactions on Signal Processing 45,February 1997：492-496.

[5]GOLDSTEIN S J,REED I S.SCHARF L L.A multistage representation of the wiener filter based on orthogonal projections[J].IEEE Transactions on Information Theory,1998,44(7):2943-2959.

[6]司晓东，蔚保国.GPS接收机空时二维抗干扰技术研究[J].测控遥感与导航定位，2010，40(3)：34-35.

[7]王永良，丁前军，李荣锋.自适应阵列处理[M].北京：清华大学出版社，2009.

[8]周柱，石峰，张尔扬，等.一种GPS接收机级联抗干扰方法[J].信号处理，2010，26(9)：56-62.

[9]DIETL G.Conjugate gradient implementation multi-stage nested wiener filter for reduced dimension processing[M].Munich University of Technology Institute for Circuit Theory and Signal Processing.2001.

[10]DIETL G,ZOLTOWSKI M D,JOHAM M.Reduced-rank equalization for EDGE via conjugate gradient implementation of multi-stage nested Wiener filter[C].IEEE 2001 VTC.VTS.2001：1912-1916.

[11]邬迪，陈庭燕.基于通用相关器的高动态GPS信号并行快速捕获[J].清华大学学报,2007,47(11):2064-2067.