基于DPT的非线性调频信号的DOA估计*
高春霞,张天骐,谭方青,魏世朋
(重庆邮电大学 信号与信息处理重庆市重点实验室,重庆 400065)
非线性调频信号是一种具有低频截获率的时变信号,它在雷达、声纳、电子对抗、生物医学、语音和通信等领域有着广泛的应用。但是对非线性调频信号的波达方向估计方法仍处于初步研究阶段。目前,人们已经提出多种非线性调频信号的形式,主要包括多项式相位信号(PPS)和正弦调频信号(SFM)。非线性调频信号的估计算法大多都是针对多项式相位信号,而对正弦调频信号的估计算法研究较少,参考文献[1]提出的基于离散多项式相位变换的方法仅讨论了对正弦调频信号的波形重构,但没有推导算法,所以现有算法还不完善。目前,还没有普遍适用的算法,故本文将非线性调频信号统一建模成高阶多项式相位信号模型。
多项式相位信号PPS(Polynomial Phases Signal)是信号处理领域中的一个具有重要意义的非平稳宽带信号。宽带信号高分辨率估计方法主要有两大类:极大似然估计(MLM)[2]和相干信号子空间方法(CSM)[3]。MLM是一种非线性最优化算法,但它运算复杂,运算量极大。而CSM存在角度预估计问题,估计精度受预估计的影响。目前国内外学者大多是针对多项式相位信号的相位系数估计[4-5]进行研究,而对多项式相位信号波达方向(DOA)估计方面的研究甚少,并且针对大于二阶的多项式信号的研究也相对较少。在现代电子对抗中,精确估计多项式相位信号的来波方向,实现超分辨测向显得非常重要。
本文研究了一种基于 Peleg[6]提出的 DPT方法,对非线性调频信号进行DOA估计。离散多项式变换(DPT)是分析恒定振幅多项式相位信号的有力工具,其主要用途是估计相位信号的系数。该方法估计模型参数,进一步推导了信号参数与模型参数的关系,得出信号参数的估计公式。且该方法能够很好地解决非线性调频信号的角度估计问题。
1 离散多项式相位变换
根据Weierstrass逼近理论[8],任一闭区间的连续函数都可以用多项式相位函数来近似。多项式相位变换(PPT)是多项式相位信号检测与估计普遍采用的一种方法,在用于离散时间信号处理时,又称为离散多项式相位变换(DPT)。本节系统地介绍了DPT,给出多项式相位变换的定义[6]。则非线性调频信号可建模成:式中,N为采样长度,Vt为采样间隔,am为实相位系数,M为相位多项式的阶数,b0、am和M统称为模型参数。

接收信号可表示为:

对于信号s(n),M阶PPS信号的一阶瞬态矩DP1[s(n),τ]、二阶瞬态矩DP2[s(n),τ]及三阶瞬态矩DP3[s(n),τ]分别定义为:

所以高阶瞬态距(HIM)定义为:

式中,τ为时延长度,0≤τ≤N-1。
M阶离散多项式相位变换 DPTM定义为DPM[s(n),τ]的离散傅里叶变换,表示为:

将式(2)代入式(8),于是有:

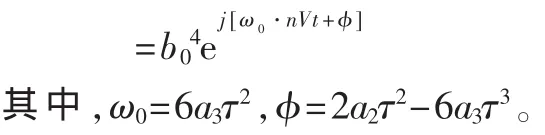
对于式(3)中的信号模型,经多项式变换将其变换为单个谐波和新的噪声。于是,可以通过计算DPM[s(n),τ]得正弦信号,然后通过FFT将在ω0处呈现峰值。从而可从峰值估计出最高阶多项式相位的系数aM:

其中,ω0=M!(τVt)M-1aM。τ的选择与最后参数估计的精度有关,根据参考文献[4]中的分析,当 M>3时,选择 τ=N/M+2;当 M≤3时,选择 τ=N/M,此时参数有较高的估计精度。
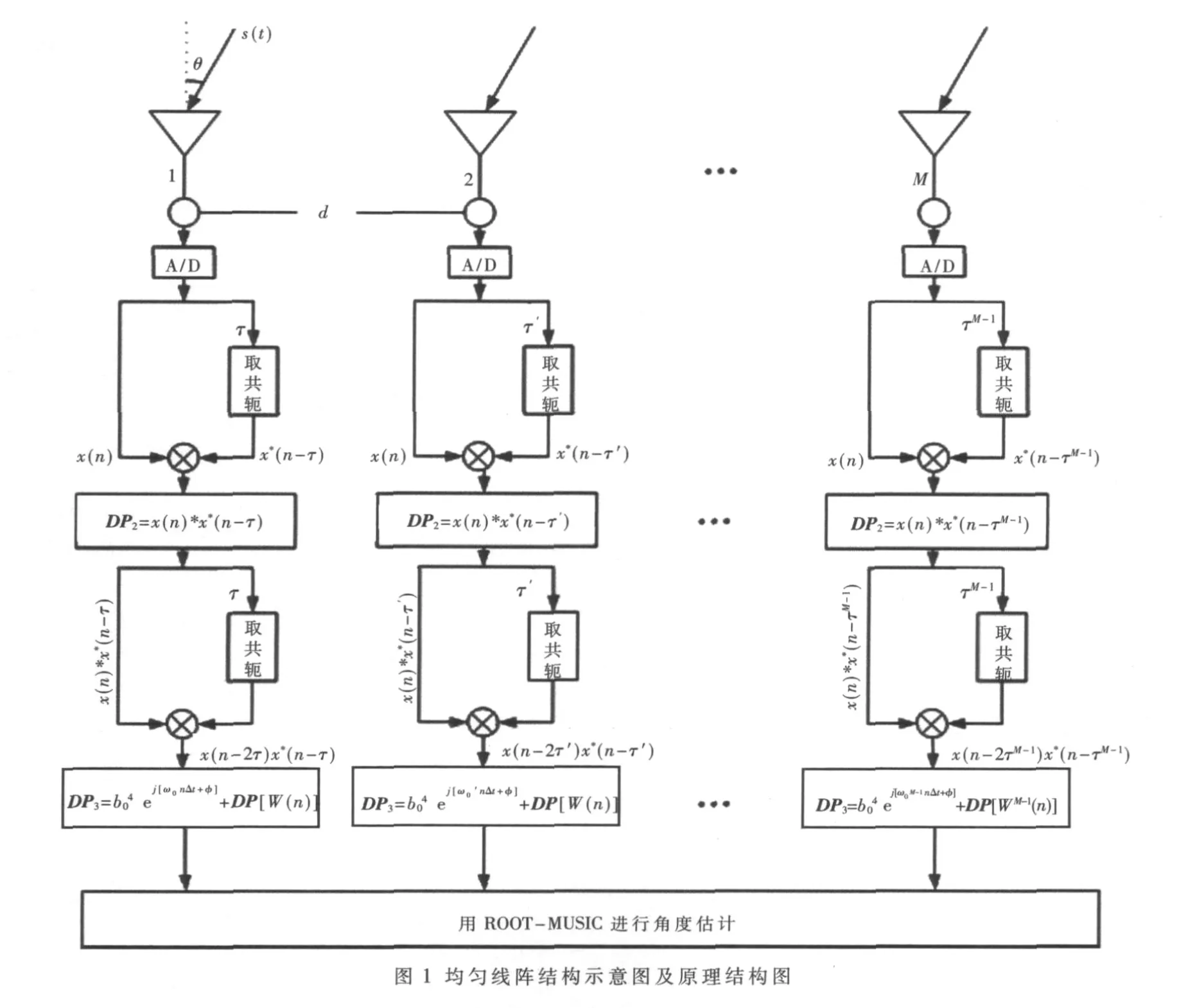
2 阵列信号模型及原理结构图
阵列模型为M个阵元的均匀线阵(ULA),阵元间距为d,如图1所示。假设有一宽带的非线性调频信号s(t),入射角为θ。其中第一个阵元作为参考阵元,则第 l个阵元上的观测信号可以表示为:

nl(t)为第l个阵元相互独立且与信号无关的高斯白噪声;τl是信号 s(t)在第 l个阵元相对于第一个阵元的延时;c为光速;DP2代表其二阶瞬时矩;DP3代表其三阶瞬时矩;DP[W(n)]代表噪声的高阶瞬时矩。
3 对单频正弦信号进行DOA估计
求根MUSIC算法是MUSIC算法的一种多项式求根形式,两者具有相同的渐进性能,但是在小样本的情况下,MUSIC算法不能分辨空间相距比较近的信号,而求根MUSIC算法能够很好地分辨。故本文采用求根MUSIC对单频正弦信号进行DOA估计。
接收信号表示为:

三阶无噪声污染信号的瞬态距表示见式(10),则:

其中,Rls和Rln分别为信号和噪声协方差矩阵。对上式协方差矩阵进行特征分解,可得λ1>λ2,…,λQ>λQ+1=λQ+2=…,λm,其中,Q为信号源个数,信号子空间是由对应大特征值组成的特征矢量,而噪声子空间是由对应小特征值组成的特征矢量。
求根MUSIC算法需要先定义如下一个多项式:

式中:ei是数据协方差矩阵中小特征值对应的M-Q个特征矢量 p(z)=[1,z,…,zM-1]T。
由以上的定义可知:当z=ejω时,即多项式的根正好位于单位圆上时,p(ejω)是一个空间频率为ω的导向矢量。由特征结构类算法可知,p(ejω)=p(z)就是信号的导向矢量,所以其与噪声子空间是正交的。因此,多项式可定义为:

也就是说只要求得式(19)的根即可获得有关信号源到达角的信息,同时发现多项式存在z*项,这使得求零过程变得复杂,可将式(19)修正为:

因为多项式 f(z)的阶数为 2(M-1),所以有(M-1)对根,且每对根是相互共轭的关系。在这(M-1)对根中有Q个根z1,…,zQ正好分布在单位圆上,即:

上式考虑的是数据协方差矩阵精确可知时的情况。在实际应用中,也就是数据矩阵存在误差时,只需求式(20)的Q个接近于单位圆上的根即可。即对于等距均匀线阵来说,根据方向导向矢量Al可知波达方向。

由以上分析,可总结出多项式相位信号波达方向估计的算法流程:
(1)初始化,令 m=M 和 xm(n)=x(n),其中 1≤n≤N-1;
(2)对信号进行高阶瞬态矩变换,可以得到变换后的单频正弦信号HIM3;
(3)对单频正弦信号HIM3进行FFT变换;

(6)替换 m=m-1,直到 m=2为止;
(7)由式(15)确定信号所对应的导向矢量;
(8)利用求根MUSIC算法进行 DOA估计,估计最终信号的波达方向。
4 仿真实验
实验一:设信号模型为:x(n)=s(n)+W(n)=b0exp[j(a1n+a2n2+a3n3)]+W(n),0≤n≤N-1。其中,a1=0.15,a2=0.2/N,a3=0.55/N2,采样点 N=360,延时 τ=N/3,离散 FFT 时变换的长度为 120×100点,快拍数为τ。
图2给出了本文多项式相位信号分别在没有噪声和SNR=20 dB时,经过瞬态矩变换后的信号实部幅值特性图。从图中可以看出,经过瞬态矩后,当没有噪声时,变换后的信号为正弦信号;当SNR=20 dB时,信号为正弦信号和新的噪声。

图3给出了的均方误差和CRB差随信噪比的变化曲线,从图中可以看出,三阶PPS在SNR大于或等于 8 dB时,此方法的估计性能越来越接近克拉美罗线,且随着信噪比的降低,仿真结果与理论结果产生较大偏差。
实验二:在实验一的基础上,对信号的波达方向进行估计,且参数和实验一相同。信号的入射角为30°。对其进行200次的Monte-Carlo仿真实验,如图4所示。

对信号的波达方向进行估计,从图4(a)可以看出,本文能较为准确地估计信号的波达方向,且随着快拍数的增加逐渐趋于稳定。图4(b)是在不同阵元的情况下误差分析,在相同信噪比的情况下,阵元数越多估计性能就越好。阵元数为10要比阵元数为6的估计性能要好一些,阵元数为6要比阵元数为4的好一些。
本文提出了一种非线性调频信号的波达方向估计方法。推导了该方法的具体步骤,并给出了相应的仿真分析,理论分析和仿真结果表明,在大于或等于8 dB时能很好地估计出多项式相位信号的来波方向,计算量大大减少,算法相对简单很多。

[1]PELEG S,PORAT B.Estimation and classification of polynomial-phase signals[J].IEEE Trans.Information Theory,1991,37(2):422-430.
[2]DORON M A,MESSER H,WEISS A J.Maximum likehood direction finding of wideband sources[J].IEEE Trans,1993,SP-41:411-414.
[3]WANG H,KAVEN M.Coherent signal-subspace processing for the detection and estimation of angles of arrival of multiple wideband sources.IEEE Trans.1985,ASSP-33(4):823-831.
[4]周良臣,杨建宇.多项式相位信号的检测与参数估计研究[D].成都:电子科技大学学报,2007.
[5]吕远,祝俊,唐斌,等.基于 DPT的非线性调频信号参数估计[J].电子测量与仪器学报,2009,23(6):63-67.
[6]PELEG S,FRIEDLANDER B.The discrete polynomial phase transform[J].IEEE Trans.Signal Processing,1995,43(8):1901-1914.
[7]BARBAROSSA S,SCAGLIONE A,GIANNAKIS G B.Product high-order ambiguity function for multicomponent polynomial-phase signal modeling,IEEE Trans.On signal processing,1998,46(3):691-708.
[8]RUDIN W.数学分析原理[M].北京:机械工业出版社,2004.
[9]万军,束坤.求根MUSIC算法与四阶MUSIC算法的分析比较[J].舰船电子对抗,2008,31(4):97-101.
[10]郑春弟,解春伟,李有才.基于实值特征值分解的求根MUSIC算法[J].数据采集与处理,2010,25(3):154-159.
[11]KUMARESAN R,TUFTS D W.Estimation the angles of arrival of multiple plane waves,IEEE Trans.on Aerospace and Electronic Systems,1983,19(1):336-339.
[12]SCHMIDT R O,Multiple emitter location and signal parameter estimation[J].IEEE Trans,1986,34(3):276-280.
[13]陈小龙,关 键,黄 勇.DOA估计算法性能分析及仿真[J].海军航空工程学院学报,2009,24(3):191-194.
[14]张贤达,现代信号处理[M].北京:清华大学出版社,2002.

