船舶管路系统中金属软管动力学性能的有限元法研究

韩淑洁

（青岛远洋船员职业学院，青岛 266071）

0 引言

在船舶管路系统中大量使用金属软管，船舶柴油机的排气管、发动机的废气回路管、机油回路管、排气歧管补偿器以及燃油冷却器中都广泛应用金属软管。金属软管由波纹管、网套和接头三部分组成[1]，在管路系统中可以对任何方向进行连接和补偿，具有可靠的密封性、高柔性、耐高低温性、耐腐蚀性等优点、还可以吸收管路的振动，起到降低噪音减少振动的作用。当管路系统收到外界干扰力的频率与金属软管的固有频率接近时，将产生共振，从而会引起船舶管路系统的泄漏和疲劳断裂，导致管路系统的失效，甚至造成巨大的经济损失和恶劣的社会影响。因此对金属软管的动力性能进行研究是非常有必要的。

目前，国内外对金属软管的研究,大都集中在静力性能，对动力学性能研究的参考文献很少。本文利用有限元仿真分析法对金属软管的动力特性进行了试验和有限元仿真分析,为避免共振，提高管路系统的质量提供了有价值的参考，也为金属软管的设计、安装和使用提供了参考。

1 金属软管振动特性的理论分析

由机械振动理论，具有有限个自由度的弹性系统振动方程为[2]：

其中：[M]，[C]，[K]分别为系统的总质量矩阵、总阻尼矩阵和总刚度矩阵；分别为振体的加速度量、速度和位移；{F(t)}为系统的外界激振力。

根据有限元分析理论，把金属软管离散为有限个三维实体单元，则每个三维实体单元的刚度矩阵为：

其中[D]为弹性矩阵；[Bi]、[Bj]为应力应变关系矩阵。

每个三维实体单元的质量矩阵为：

其中[Ni][Nj]为形函数矩阵，ρ为单元质量密度。

根据实体单元的节点自由度与金属软管的总体节点自由度是一一对应的原则，把单元刚度矩阵[Kij]e组集成结构的总体刚度矩阵[K]，把单元质量矩阵[Mij]e组集成结构的总质量矩阵[M]，节点上的附加质量块，也组集到总体质量矩阵[M]中。

在模态分析过程中，外界激振力 {F(t)}={0}，系统处于自由振动状态，结构阻尼较小，忽略不计，由此可得金属软管无阻尼自由振动的微分方程：

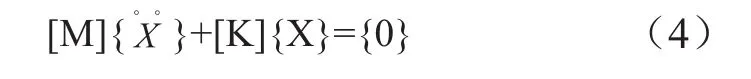
其特征方程为：

式中ω为系统的固有圆频率。

要使单元质量矩阵不为零，则特征方程（5）的系数行列式必须为零，即：

求解式（6）便可得到金属软管自由振动的固有频率。

瞬态振动响应分析，是指系统在动载荷作用下（即强迫振动时）所产生的位移、速度和加速度[2]。可以通过求解有限个自由度的弹性系统的动力方程（1）来求得。

2 金属软管动态有限元模型的建立

单元的选取与静态有限元建模类似，根据金属软管在振动中的材料非线性、几何非线性和大变形等非线性特点，金属软管动态有限元建模时，波纹管选用八节点空间壳单元shell93，网套钢丝选用三维梁单元Beam189描述。利用耦合建立波纹管层与层之间的关系，利用约束方程建立最外层波纹管与最内层网套之间的关系。

由于金属软管两侧端部的法兰盘对静力学性能影响甚小,所以在静力学建模的时候，没有对其进行考虑。但在研究金属软管的动力学性能时，两侧端部的法兰盘及其相连附件的质量就不能忽略了。根据有限元分析理论，金属软管两侧端部的法兰盘，选用体单元描述比较合适，但采用体单元与波纹管处的壳单元的连接无法实现，所以本文在金属软管动态建模过程中忽略了法兰盘形状的影响，只考虑其质量的影响。把法兰盘及其相连的其他构件的质量，运用质量单元mass21，均匀分布到一个当量半径的圆周节点上作为附加质量块，也采用shell93单元对其进行描述。在ANSYS中建立的金属软管的动力学有限元模型如图1所示。

图1 金属软管的动力学有限元模型

由于金属软管在实际工作中主要作为管路系统的连接件，其两端均与刚性管路连接，而刚性管路的柔性很少，所以在分析金属软管的振动特性时，采用两端均为固定端模拟其边界条件。

3 金属软管的振动模态分析

3.1 金属软管振动模态分析试验

金属软管振动模态的测定试验采用锤击法。实验时，用安装有力传感器的力锤轴向敲击贴有电阻应变片的金属软管上的若干个测试点，使其产生轴向的振动，力传感器得到激振力的信号并将之转为电荷信号，电荷信号经QL-021二通道电荷电压放大器放大后转化成适合测量的电压信号。通过动态应变仪和光线示波器记录1秒钟内应变的变化次数，即为金属软管的轴向自振频率，利用振动分析软件CRAS V5.1进行分析，作为有限元分析可靠性的依据。

图2 脉冲锤的结构简图及其力学模型示意图

外界激振力脉冲的振幅大小和持续时间长短是由力锤决定的，力锤的锤头垫越硬，则碰击的时间越短，力脉冲越窄，频率范围越广。本实验中由于金属软管是不锈钢材料，采用钢垫敲击。

3.2 金属软管振动模态的有限元法分析

ANSYS的模态分析中，模态提取的方法有：子空间法（Subspace）、分块兰索斯法(Block Lanczos)、凝聚法(Reduced)、非对称法(Unsymmetric)、阻尼法（Damped）和 QR阻尼法(QR Damping)等[3]，分块兰索斯法求解精度高，计算速度快等，特别适合大型的具有对称特征值大型结构的求解问题，所以本文在利用有限元法对金属软管进行模态分析时，采用分块兰索斯法(Block Lanczos)来提取其模态。选取表1所示两个几何尺寸的金属软管，对其两端固定，利用参数化的有限元模型，对金属软管的振动模态进行分析。试件的材料为1Cr18Ni9Ti，其密度 ρ=7.8×103kg/m3,弹 性 模 量 E=196GPa， 塑 性模量 EP=257Mpa，泊松比 µ=0.3， 屈服极限 σs＝257MPa。经有限元仿真分析得到的金属软管的轴向固有频率与用锤击试验法测得的轴向固有频率的对比如表2所示。

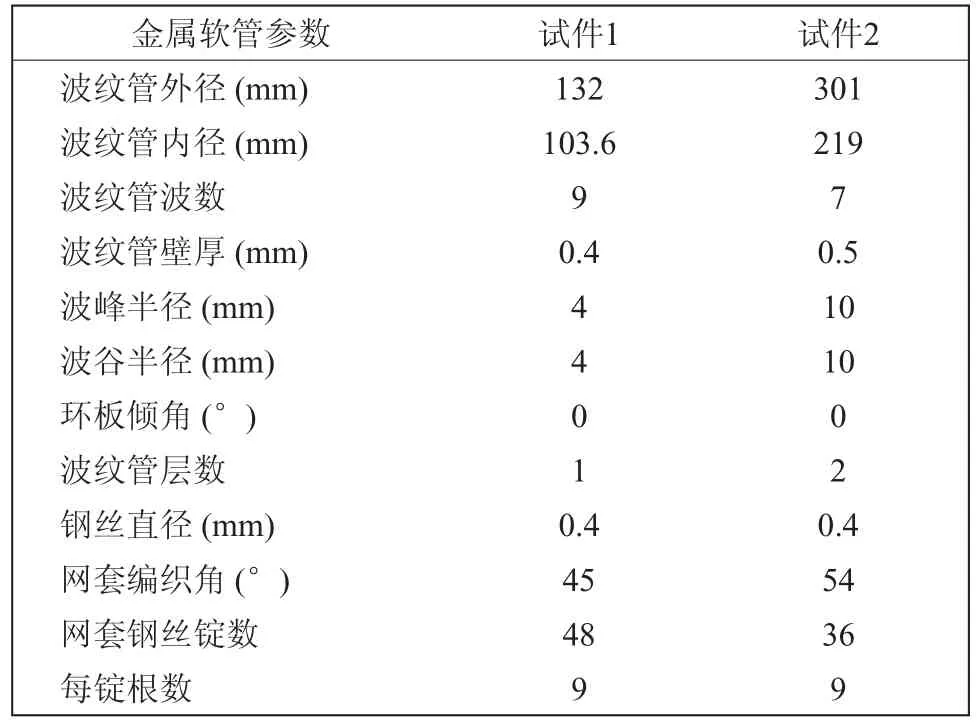
表1 金属软管的几何尺寸参数

表2 有限元值与实验值的轴向固有频率比较

从表2可以看出：有限元仿真分析果与锤击法试验结果非常接近，从而证明了金属软管动态有限元模型和边界条件模拟的可靠性。从表2还可以看出试件1和试件2的二阶轴向固有频率是一阶轴向固有频率的两倍左右，这与振动模态理论和实际经验都非常吻合。

4 金属软管的谐响应分析

利用已经证明的可靠的动态有限元模型，对表1中的试件1进行振动模态分析，得到前十阶固有频率如表3所示。在试件1的外表面上取一点，施加径向简谐激振力，力幅为500N，频率为1000Hz，对其进行谐响应分析，图3给出了金属软管上某点在0～1500Hz频率范围内的径向位移与频率的关系曲线。

从图3可以看出，在激振点处，振动位达到最大值。当外界激振力的频率大约为345Hz、471Hz、613Hz、711Hz、890Hz、954Hz和 1145Hz时，金属软管上该测试点的径向位移响应也出现峰值。而这些频率值是用有限元法仿真计算出的固有频率值（如表3所示）。这是由于外界干扰力的频率与金属软管本身的固有频率接近时，系统发生共振，从而使径向位移增大。这与机械振动理论完全吻合，进一步证明了本文的金属软管动力性能有限元分析程序的可靠性。从图3还可以看出：在激振点处，振动位达到最大值，离激振点很近的地方，振动位移相应已经很小了，充分证明了金属软管的良好的吸振能力。通过参数化的金属软管动力性能分析程序对大量试件进行分析后发现：金属软管吸收横向振动的能力要比吸收轴向振动的能力强的多。

表3 金属软管的前十阶固有频率值

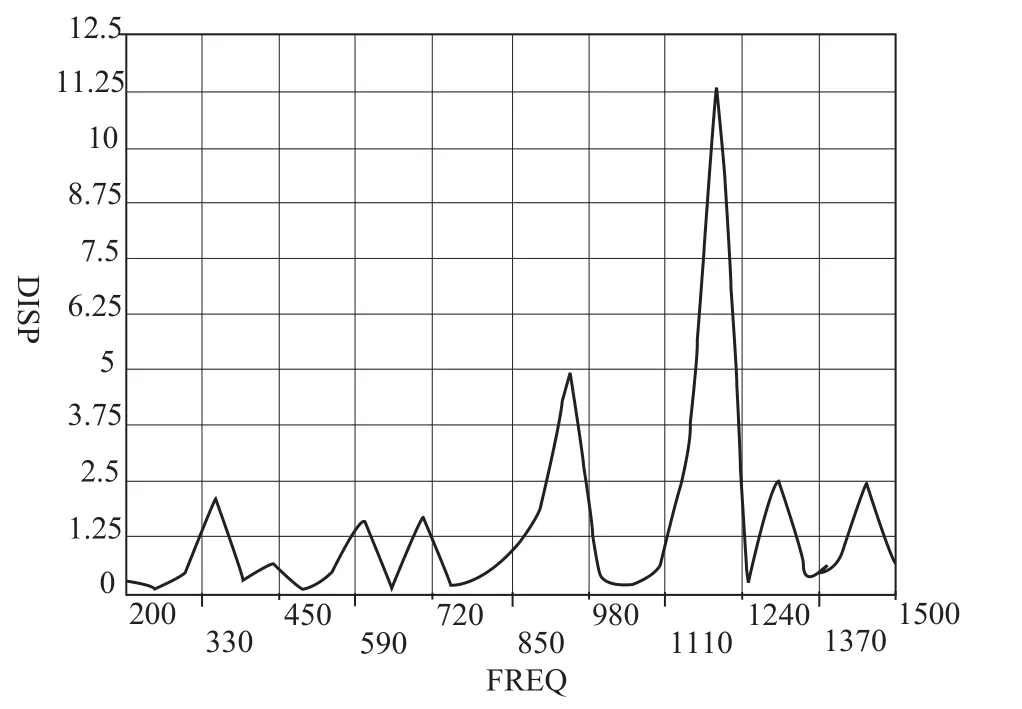
图3 径向位移与频率的关系曲线

5 金属软管的瞬态振动响应分析

对试件1施加径向瞬态激振力的作用，沿金属软管的半径方向，把一个周期内的位移分为十二个增量子步进行施加，由于金属软管属于非线性问题，在每个增量子步过程中刚度矩阵都是被修改的，所以采用直接积分法中的显式积分法进行瞬态响应分析，以避免矩阵求逆的运算。为便于观察，下面仅给出波纹管的动应力分布云图。图4至图7分别给出了有限元动态分析程序得到的波纹管在正最大位移（T=0.025s），平衡位置（T=0.05s）、正最大位移（T=0.075s）、平衡位置（T=0.1s）四个时刻的Von Mises应力云图。

图4 T=0.025时瞬态激励的动应力云图

图5 T=0.05时瞬态激励的动应力云图

图6 T=0.075时瞬态激励的动应力云图

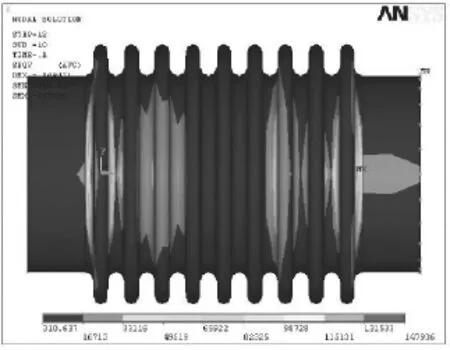
图7 T=0.1时瞬态激励的动应力云图

从图4至图7可以看出，在径向瞬态激励下，金属软管的最大动应力发生在波纹管外表面靠近两端部的波纹处，第一个波和第二个波之间的波谷圆弧处动应力最大。另外，利用参数化有限元分析程序对多层波纹管进行分析可以发现：瞬态激励下，金属软管的最大动应力总是发生在最外层的波纹管上。也就是说，金属软管在径向瞬态激励下，动应力最大的部位是：最外层波纹管上靠近两端部的第一个波和第二个波的波谷处。在金属软管瞬态激励振动情况下，最大动应力处最先破坏，这一分析结果与实际情况非常吻合。

6 结束语

本文利用ANSYS中的参数化设计语言APDL建立了金属软管的动态有限元模型，对金属软管的振动模态进行了分析，并与试验结果进行了对比，证明了有限元动力学模型的可靠性。进一步对金属软管的谐响应和瞬态振动响应相应进行了分析，分析结果与理论和实际经验非常吻合。本文的研究成果对全面把握金属软管的动力学性能、提高管路系统的质量和避免共振有重要的实用价值，对金属软管的结构设计、安装和标准化也提供了有益的参考。

[1] 刘鸿文.板壳理论[M].浙江大学出版社, 1987.

[2] 胡海岩, 孙久厚, 陈怀海.机械振动与冲击[M].航空工业出版社, 2002.

[3] 刘涛, 杨风鹏.精通ANSYS[M].清华大学出版社, 2002.

[4] 傅志方, 华宏星.模态分析理论与应用[M].上海交大出版社, 2000.

[5] K.J.巴斯.工程分析中的有限元法[M].机械工业出版社,1991.