基于SESAM软件的驳船系泊及锚泊缆索强度校核

仲 鹏

(江阴赛福咨询有限公司，江苏 无锡 214400)

0 引言

在船舶种类中，工程驳船是一种类型繁多，用途广泛的船型。目前驳船在系泊或锚泊状态下缆索的强度，通常是通过规范的经验公式进行校核的。由于船型及工作环境的特殊性，这些经验公式的计算结果往往不够精确。本文将运用大型有限元软件SESAM建立驳船的有限元模型，运用三维势流理论分析其水动力特征，从而可以计算驳船所受到的环境载荷，并在此基础上，分析驳船在不同的系泊和锚泊工况下，缆索受到的张力，校核系泊缆索的强度。

1 基本理论

SESAM软件是目前计算船舶与海洋结构物的环境载荷较为先进的软件之一，它采用的理论为三维势流理论，计算作用于驳船上的波浪载荷。

船体的外载荷矩阵可以表达成如下形式［1～4］:

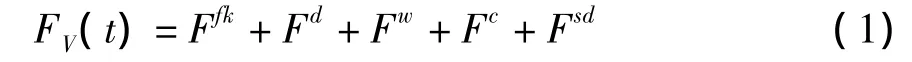
式中:FV(t)为船体的外载荷，Ffk为佛汝德－克雷洛夫力，Fd为波浪绕射力，Fw为风力，FC为流力，Fsd为二阶漂移力。

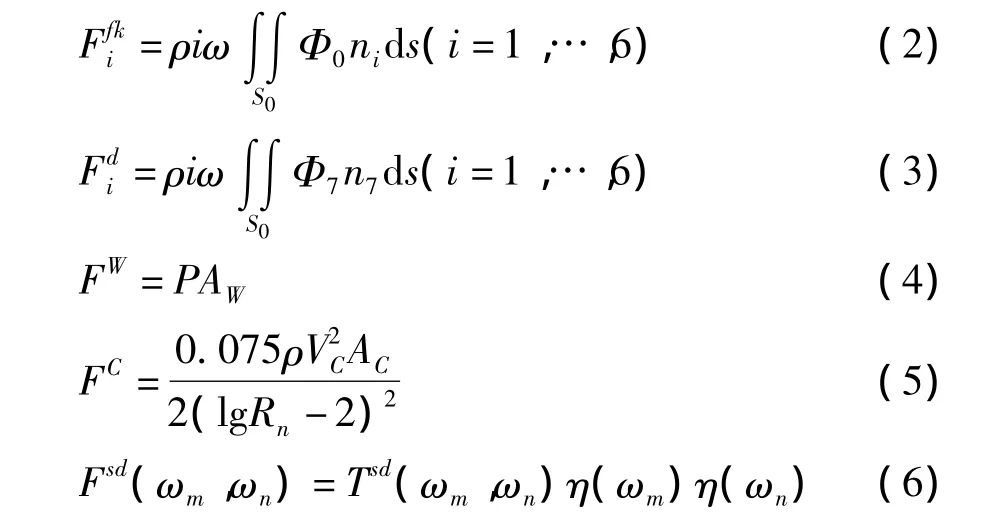
式(2)～式(6)中:Φ0和Φ7分别代表波浪的入射势和绕射势，P为风压，Vc为流速，Aw和Ac分别为受风和受流面积。Tsd为二阶传递函数，η(ωm)和 η(ωn)分别为2种频率的波的幅值，i为次数，ω为频率，ρ为密度，Rn为雷诺数。

采用 Wilson － theta［5］或者 Runge － Kutta［6］数值积分方法对其进行数值求解，可以得到作用于驳船上的外环境载荷。

2 驳船概况

2.1 驳船主要参数

驳船主要参数见表1。

表1 驳船主要参数

2.2 系泊及锚泊布置

(1)码头顶靠滚装的系泊布置

码头顶靠滚装的系泊布置如图1所示。

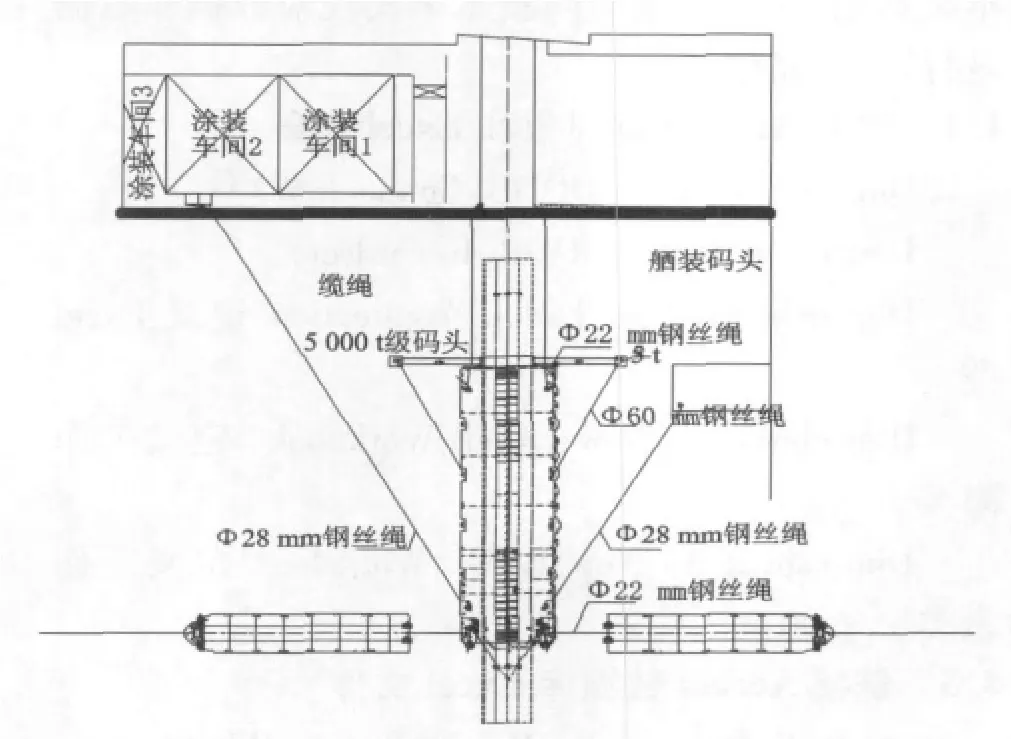
图1 码头顶靠滚装时系泊布置图

(2)码头系泊布置

钢丝绳码头系泊布置如图2所示。

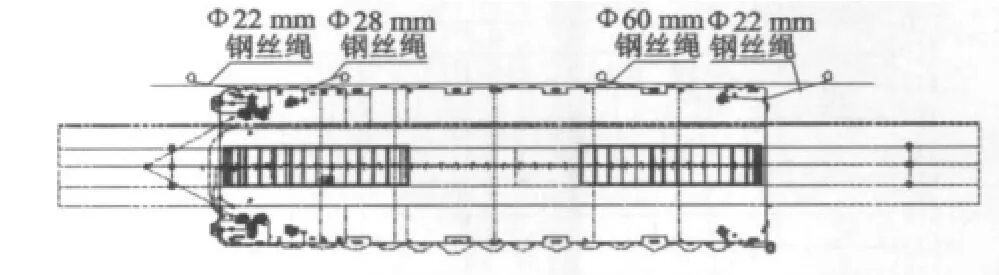
图2 码头系泊布置

(3)航行中避风锚泊布置

航行中避风锚布置如图3所示。

图3 航行中避风抛锚布置

(4)大节段抛锚定位

除上述主要系泊布置外，在桥面的运输和安装过程中，亦有专门的锚泊布置方案。图1～图3可视为沿着来流(首向或者尾向来流)，而大节段抛锚定位时则是侧向来流。因此，在以下工况分析中，则分别计算驳船受到的首尾向和侧向的环境载荷。图4、图5分别为大节段抛锚定位方案1、方案2。

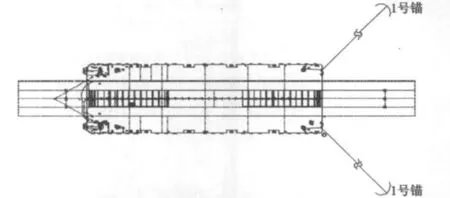
图4 大节段抛锚定位(方案1)

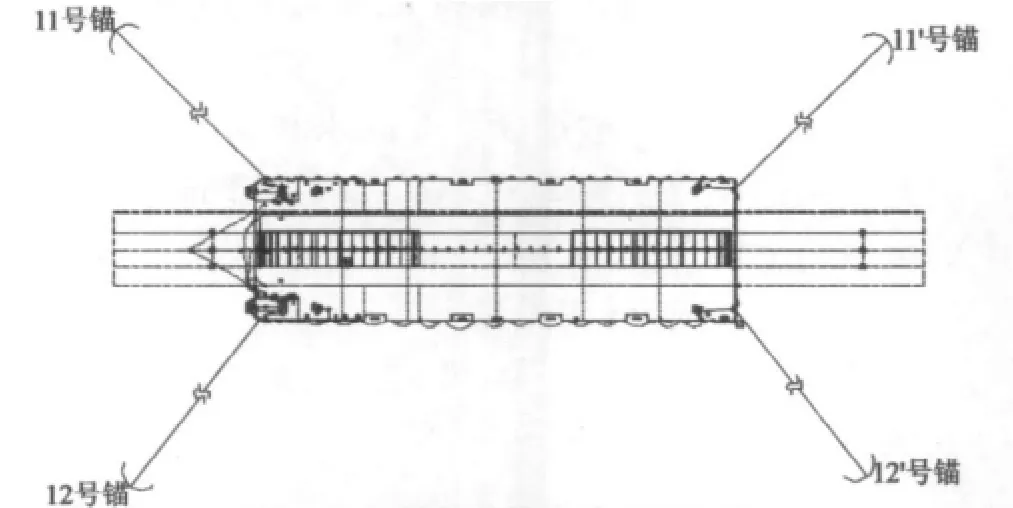
图5 大节段抛锚定位(方案2)

2.3 环境参数

计算过程中，取流速为3 m/s，风速为15 m/s，波浪取规则波，波高取0.5 m，周期4 s。由于创建工况时选择的是规则波工况，而风载荷为随机载荷，故先将风载荷与浪、流载荷分离开来分别计算。先计算流和浪的组合工况，最后加上风载荷。计算其首尾向载荷时采用流和浪与X轴成0°，以及侧向载荷时流和浪与X轴成90°的情况。工况选择时，主要考虑2种工况:2.5 m吃水以及3.5 m吃水。由于装载了桥梁，故这2种受风面积相对较大，视为危险工况进行计算。

3 有限元模型的建立

本文主要计算驳船的环境载荷，故只需建立驳船的外表面模型即可。另外全船左右对称，只需建立一半的模型。取网格长度为2 m。驳船有限元模型、水动力模型分别如图6、图7所示。

图6 驳船有限元模型

图7 驳船水动力模型

由于软件的限制，而不能独立显示驳船所受的首尾向和侧向的环境载荷，但是可以得出作用于锚链上的拉力。本文将采用一种特殊方法进行处理:求驳船的首尾向波流载荷的时候，假设驳船通过一平行于X轴的系泊锚链连接于河底，流和浪与X轴成0°(沿首尾向)，此时求得的系泊锚链靠近导缆孔处的拉力沿首尾方向的分力，即为驳船所受到的首尾向波流载荷。同理，求驳船的侧向波流载荷的时候，假设驳船通过一平行于Y轴的系泊锚链连接于河底，流和浪与X轴成－90°(沿侧向)，此时求得的系泊锚链靠近导缆孔处的拉力沿侧方向的分力，即为驳船所受到的侧向波流载荷。计算时，系泊锚链的材料、尺寸、位置做简单处理，因为它与所受的拉力无关。2种假设的分析模型分别见图8和图9。

4 计算结果

4.1 浪流载荷的计算结果

图10为工况1(3.5 m吃水)时，缆索在侧向波流载荷作用下的张力时间历程，图11为工况1(3.5 m吃水)时，缆索在首尾向波流载荷作用下的张力时间历程。图12为工况2(2.5m吃水)时，缆索在侧向波流载荷作用下的张力时间历程;图13为工况2(2.5 m吃水)时，缆索在首尾向波流载荷作用下的张力时间历程。

图8 首尾向受力分析模型

图9 侧向受力分析模型

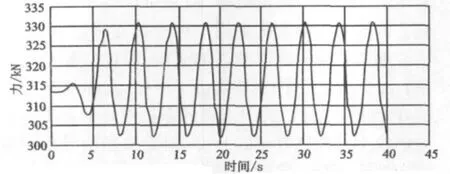
图10 工况1(3.5 m吃水)侧向波流环境载荷

4.2 风载荷的计算结果

本文取7级风，平均风速v=15.69 m/s，风速v与风压ω有如下关系:

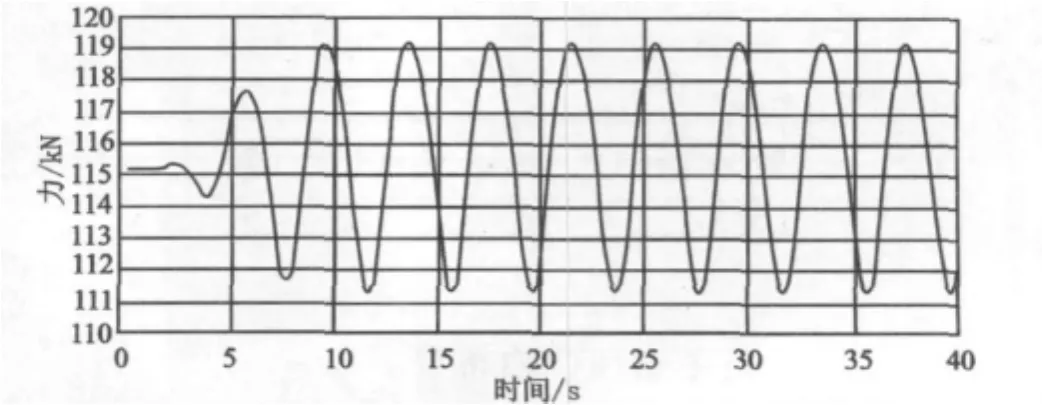
图11 工况1(3.5 m吃水)首尾向波流环境载荷

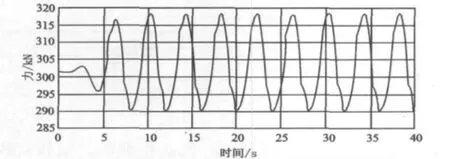
图12 工况2(2.5 m吃水)侧向波流环境载荷

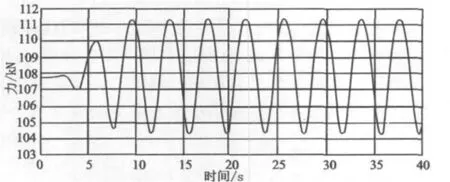
图13 工况2(2.5 m吃水)首尾向波流环境载荷

式中:γ为空气容重，kN/m3;g为重力加速度，m/s2。在标准大气压情况下，设γ=0.012018 kN/m3，g=9.81 m/s2，则有

将风速v代入式(8)，便可得出风压。

设结构物的迎风面积为A，则结构的风载荷为F=Aω。

本文所研究的驳船3.5 m吃水和2.5 m吃水工况的受风面积分别为2595 m2和2782 m2，故驳船的风载荷曲线分别为399.3 kN和428 kN。

4.3 环境总载荷计算结果

将上述各种工况下的风、浪、流载荷进行汇总，其结果见表2。

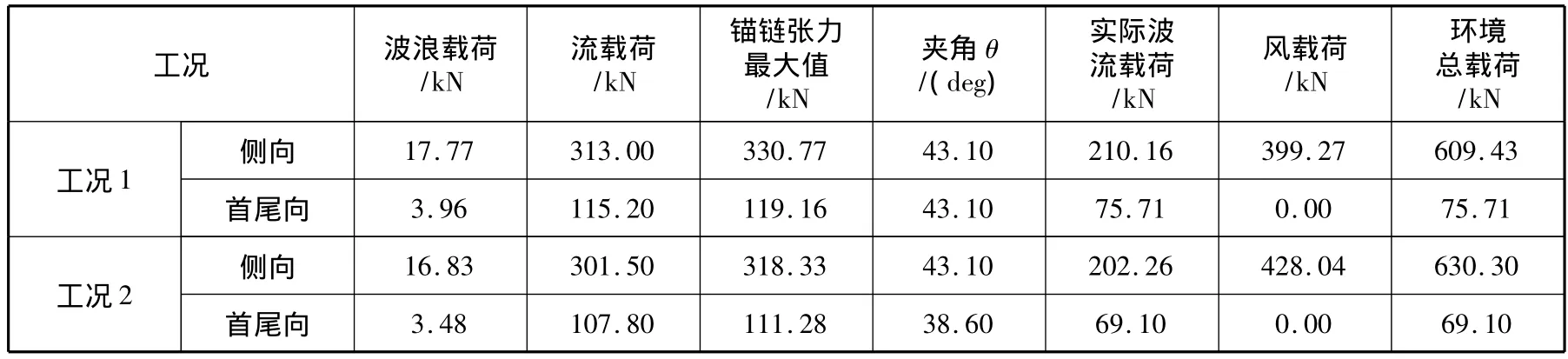
表2 环境总载荷计算结果

表2中，波浪载荷一项表示波浪对锚链张力的 作用，而实际的波浪载荷则需要乘上夹角的余弦值。由表2可以发现，工况2(2.5 m吃水)的侧向载荷是最大的，为 630.3 kN。

5 系泊及锚泊时缆索的强度校核

5.1 码头顶靠滚装时缆索系泊强度校核

根据图1码头顶靠滚装的系泊布置情况，认为船舶受到最为恶劣的工况2(2.5m吃水)的侧向载荷的作用，此时的最大侧向荷载F为630 kN。根据力平衡和弯矩平衡原理，建立力学模型，并对其进行求解，如图14所示。其中T为钢丝绳的张力，T1为系泊于5000 t级码头系缆墩上的钢丝绳张力，T2为系泊于涂装车间钢丝绳的张力，T3为驳船尾部系泊于码头的钢丝绳张力，T4和T5分别为码头作用于驳船尾部的支反力，T6为驳船首部连接于拖船的钢丝绳的张力，可以得到:与涂装车间连接的钢丝绳的张力为376.5 kN;与码头相连的钢丝绳的张力为330 kN;与定位船连接的钢丝绳的张力为121.6 kN。

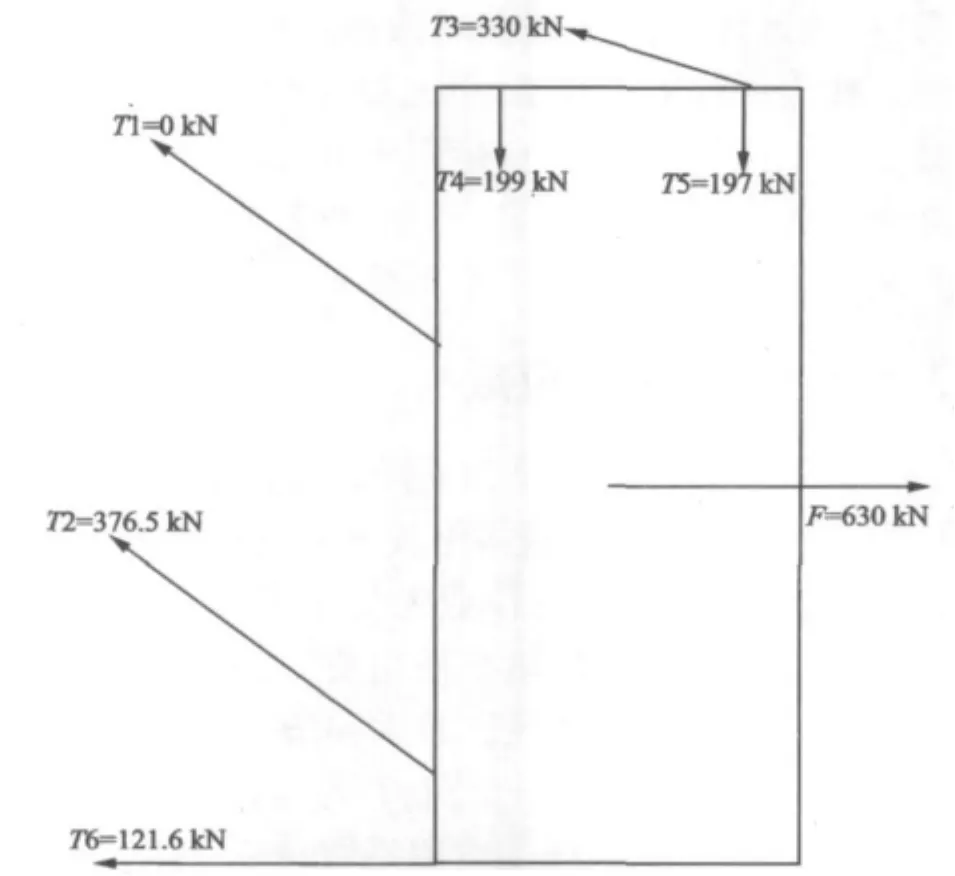
图14 码头顶靠滚装时缆索系泊受力分析模型

根据规范，取钢丝绳的安全系数为2.5，则与涂装车间连接的钢丝绳要求能够承受的张力不小于941.5 kN，与码头相连的钢丝绳要求能够承受的张力不小于825 kN，与定位船连接的钢丝绳要求能够承受的张力不小于302.5 kN。根据设计方提供的尺寸，T2和T3处为Φ46 mm钢丝绳，其破断负荷为1320 kN;T6处为Φ28 mm钢丝绳，其破断负荷大于400 kN。因此，这3条钢丝绳的强度能满足要求，在外载荷的作用下不会破断。

5.2 码头系泊时缆索强度校核

根据图2码头系泊布置情况，认为船舶受到工况2(2.5 m吃水)的侧向风载荷的作用，此时的最大侧向荷载为428.04 kN，首尾向受到波流载荷的作用力66.93 kN。若4根缆索横向放置，根据力平衡和弯矩平衡原理，可以求得作用于这4根缆索上的张力为108 kN。取钢丝绳的安全系数为2，则钢丝绳要求能够承受的张力不小于226 kN。根据设计方提供的尺寸，这4根缆索中有2根的直径为Φ46 mm，另外2根的直径为Φ22 mm，其破断负荷均大于226 kN。因此，这4根钢丝绳的强度能满足要求，在外载荷的作用下不会破断。

5.3 航行中避风抛锚时缆索强度校核

根据图3航行中避风抛锚的系泊布置情况，认为船舶受到工况1(3.6 m吃水)的首尾向载荷的作用，此时的最大首尾向载荷为75.7 kN，而认为这一抛锚过程，船首始终正对风浪流。根据力平衡和弯矩平衡原理以及悬链线方程，可以求得:AM2Φ52 mm电焊有档锚链的张力为40 kN。

锚链的安全系数为2，锚链要求能够承受的张力不小于80 kN，而锚链的破断负荷为1479 kN，故满足强度要求，在外载荷的作用下不会破断。

5.4 大节段抛锚定位方案1的缆索强度校核

根据图4航行中避风抛锚的系泊布置情况，认为船舶受到最为恶劣的工况2(2.5 m吃水)的侧向载荷的作用，此时的最大侧向载荷为630 kN。根据力平衡和弯矩平衡原理以及悬链线方程，建立力学模型，并对其进行求解，如图15所示。其中，T1和T2分别为顺流和逆流的锚链张力，T3为桥墩的支反力。可以求得:AM2Φ52 mm电焊有档锚链的张力为 577.5 kN。

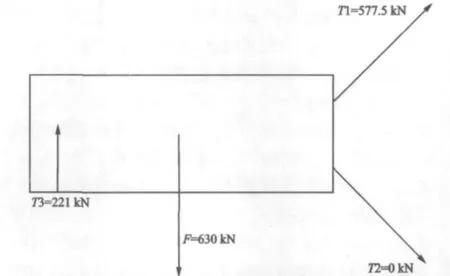
图15 大节段抛锚定位时缆索系泊受力分析模型(方案1)

锚链的安全系数为2，锚链要求能够承受的张力不小于1155 kN，而锚链的破断负荷为1479 kN，Φ46 mm钢丝绳破断负荷为1320 kN，故设计方案满足强度要求。在外载荷的作用下锚链不会破断。

5.5 大节段抛锚定位方案2的缆索强度校核

根据图5航行中避风抛锚的 系泊布置情况，船舶受到最为恶劣的工况2(2.5 m吃水)的侧向载荷的作用，此时的最大侧向荷载为630 kN。根据力平衡和弯矩平衡原理以及悬链线方程，建立力学模型，并对其进行求解，见图16。其中，T1、T2、T3、T4分别为4根锚链的张力。可以求得:AM2Φ52 mm电焊有档锚链的张力为445.5 kN。锚链的安全系数为2，锚链要求能够承受的张力不小于891 kN，而锚链的破断负荷为1479 kN，Φ46 mm钢丝绳破断负荷为1320 kN，故设计方案满足强度要求。在外载荷的作用下锚链不会破断。

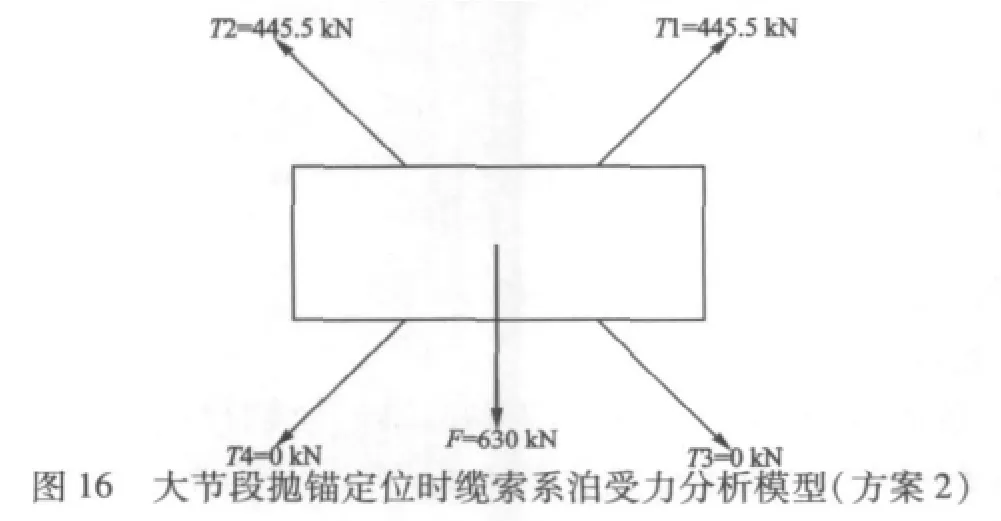
［1］肖越.系泊系统时域非线性计算分析［D］.辽宁:大连理工大学，2005.

［2］戴仰山，沈进威，宋竞正.船舶波浪载荷［M］.北京:国防工业出版社，2007.

［3］Y M Low，R S Langley.Time and frequency domain coupled analysis of deep －water floating production systems［J］.Applied Ocean Research，2006，(28):371 －385.

［4］陈新权.深海半潜式平台初步设计中的若干关键问题研究［D］.上海:上海交通大学，2007.