BIBD 循环置换矩阵的多进制LDPC码构造✴

刘冰，陶伟，窦高奇，高俊

（1.解放军91469部队，北京100841；2.海军装备研究院，北京100161；3.海军工程大学电子工程学院，武汉430033）

BIBD 循环置换矩阵的多进制LDPC码构造✴

刘冰1，3，陶伟2，3，窦高奇3，高俊3

（1.解放军91469部队，北京100841；2.海军装备研究院，北京100161；3.海军工程大学电子工程学院，武汉430033）

提出了基于均衡不完全区组设计（Balanced Incomplete Block Design，BIBD）的多进制准循环LDPC（Low-Density Parity-Check）码代数构造方法。在该构造方法中提出了广义多进制位置向量的概念，并根据广义多进制位置向量和BIBD法对指数矩阵进行广义二维扩展，构造出具有循环置换子矩阵的多进制校验矩阵，由此得到girth不小于6的多进制LDPC码。仿真结果表明，采用FFT-QSPA（基于快速傅里叶变换的多进制和积算法）对构造出的LDPC码进行译码，在AWGN信道下相比于同参数的RS码来说可以取得明显的编码增益，并且优于多进制Mackay码。

多进制低密度奇偶校验码；准循环；均衡不完全区组；广义多进制位置向量；二维扩展

1 引言

均衡不完全区组设计（Balanced Incomplete Block Design，BIBD）［1-2］可用于构造多进制低密度奇偶校验（Low-Density Parity-Check，LDPC）码，其是组合数学中组合设计的一个重要问题。BIBD构造法属结构化构造法［3-6］，相比于随机化构造法［7，8］，具有特定的结构，尤其是循环或准循环（Qusic-Cyclic，QC）结构，优势在于编码实现简单，仅用简单的移位寄存器就可实现线性化的编码复杂度［9］，这对工程的实际应用具有重要的作用和意义。将二进制LDPC码扩展到高阶伽罗华域上形成多进制LDPC码［10］，一般来说，精心设计的多进制LDPC码具有较二进制更好的性能，特别是在中短帧长度。但是多进制LDPC码面临着两大难题：编码和译码的复杂度过高。对于编码来说，可以采用准循环结构的LDPC码，达到线性化编码的目的［9］；而对于译码来说，基于快速傅里叶变换的多进制和积算法（Fast Fourier Transform based q-ary Sum-Product Algorithm，FFT-QSPA）［11］在取得优越性能的同时，有效地降低了多进制LDPC码的译码复杂度。

准循环LDPC码作为一类非常重要的LDPC码分支，其构造方法汲取和借鉴了代数、几何等领域的数学理论，多角度迅速发展。Shu Lin课题研究小组首次提出了基于有限几何［12］、有限域［13］、循环置换矩阵［14］和BIBD［3，15］等理论的系统化二进制LDPC码构造方法。之后在二进制构造的基础上首次提出了基于有限几何［16］和有限域［17］的多进制准循环LDPC码的系统化构造方法，相比于RS码而言，构造出的码字在AWGN信道下可以取得很大的编码增益。Bassem Ammar将BIBD的一种特殊子类首次运用于二进制LDPC码的设计中［2］，该LDPC码校验矩阵的构造方法采用的是BIBD关联矩阵。BIBD构造多进制校验矩阵时，其元素取自GF（pm），其中p是素数，m为正整数，但是低复杂度的FFT-QSPA只能对GF（2l）域上构造的码字进行译码［11，18］，因此在采用BIBD循环置换矩阵构造多进制LDPC码时，两者的适用前提条件是有所区别的。针对这一问题，本文提出了基于广义多进制位置向量的广义二维扩展方法以及两类基于BIBD广义循环置换矩阵（Circulant Permutation Matrix，CPM）的多进制QC LDPC码的构造方法，该方法可取得girth至少为6的规则多进制QC LDPC码。通过对指数矩阵进行基于广义多进制位置向量的水平扩展和基于部分周期循环特性的垂直扩展，使得构造校验矩阵非零元素的位置和数值分别取自GF（pm）和GF（2l）域。提出的广义二维扩展优势在于：可适用于非2幂次大小循环置换子矩阵的构造和2的幂次大小循环置换子矩阵的拓展；构造出的多进制LDPC码可采用低复杂度高性能的FFT-QSPA译码算法。

文章的组织结构如下：第2节提出了基于广义多进制位置向量的广义二维扩展方法，第3节由上述扩展方法构造出了两类BIBD循环置换矩阵的多进制LDPC码，第4节通过仿真结果比较了构造出多进制LDPC码的性能，最后是结束语。

2 BIBD与多进制准循环LDPC码构造

多进制规则LDPC码C由多进制稀疏校验矩阵H的零空间所定义，其具有以下结构化性质：每行的重量（非零元素的个数）为dc；每列的重量为dv；行列（RC）约束，即任何两行（或两列）之间位置相同的非零元素个数不大于1。这样构造出来的校验矩阵是规则的，由其零空间给出的码C称为（dv，dc）规则LDPC码。RC约束保证了两点：由H的零空间给出的LDPC码C的Tanner图girth至少为6；码的最小距离至少为dv+1。如果H的行与（或）列具有不同的重量，那么H的零空间将给出一个非规则LDPC码。LDPC码的误码性能由码结构特性的诸多因素共同决定，主要因素有Tanner图的girth、短环的结构、处于某一码字上短环的数量、校验矩阵的选择和码字的最小距离等。目前只能通过仿真和基本的分析来考查这些起决定作用的因素，它们之间还没有明确的结论性关系，有待进一步研究。最影响码字性能的短环是长度为4的环，所以这类短环在校验矩阵的构造时应予以避免，这是目前绝大多数LDPC码构造时首要考虑的问题，同时也满足了定义中的行列约束性质。

具有q个元素的阿贝尔群G的一个BIBD是指G的n个r子集，记为B1，B2，…，Bn，称为区组（Blocks），它们满足如下条件［1］：每个元素恰好在n个区组中的k个出现；任一元素对恰好在n个区组中的λ个出现；每个区组中元素的个数r与X中的元素总数q相比非常小。于是，一个BIBD由n，v=q，r，k和λ5个参数来刻画。除了用区组的表示方式外，一个BIBD可以用一个GF（q）域上的q×n关联矩阵H=［hi，j］来描述：其行对应着X的q个元素；其列对应着该设计的n个区组；当且仅当第i个元素xi

属于第j个区组Bj时，hi，j≠0且hi，j∈GF（q），否则，hi，j=0。这个矩阵被称为设计的关联矩阵H，H的列重和行重分别是r和k。根据BIBD的第2个条件，H的两个行向量具有λ个公共的1分量。如果λ=1，H就满足了LDPC码定义的所有性质，于是H的零空间给出了一个长度为n的（dv，dc）规则LDPC码，其Tanner图中没有长度为4的环。这是基于BIBD最直接构造LDPC码的方法。对于（n，v，r，k，1）BIBD素域构造方法可查阅相关文献［1-3，15］。而本文构造的多进制校验矩阵的基矩阵是基于Bose BIBD理论，首先阐述下面一个定理［1］。

定理：令G=｛x（1），x（2），…，x（q）｝是具有q个元素的阿贝尔群。对于G中的每一个元素x（i），重复f次，并记为x（i）1，x（i）2，…，x（i）f，这样通过群G可以得到具有fq个元素的集合X。将fq个元素分为q组，X的s个r子集，记为B1，B2，…，Bs，称为区组（Blocks），它们满足如下条件：在s个区组中的sr个元素中，k个元素属于q组中的一组；s个区组中元素的差是对称重复的，且每一个出现λ次。

通过将G中每个元素逐个加到每一个区组B1，B2，…，Bs上，可以得到一个具有参数v=fq，n=sq，r，k和λ的BIBD，这里，区组B1，B2，…，Bs被称为基本区组。本文校验矩阵指数矩阵的构造则是建立在基本区组上。

BIBD构造校验矩阵中的循环阵大小都是素数的幂pm，将BIBD构造的校验矩阵扩展到多进制上，可直接在GF（pm）域上进行，即在BIBD决定的位置上随机或有规律地填入GF（pm）域中的非零值。但是这种方法构造出的多进制LDPC码只能采用QSPA算法或其衍生的算法来译码，而不能采用低复杂度的FFT-QSPA译码算法。采用QSPA算法存在的缺陷是复杂度较高，不利于工程实现，但是应用FFT -QSPA的前提是域的阶数必须为2的幂，这正是构造基于BIBD多进制LDPC码时的矛盾所在。因此，本文构造的基于BIBD多进制LDPC码会涉及到GF（pm）和GF（2l）两个不同的域，多进制LDPC码校验矩阵中非零元素的位置是由GF（pm）域上BIBD设计决定的，而非零元素的取值则是在GF（2l）域上进行的。这两个域的具体关系如下：

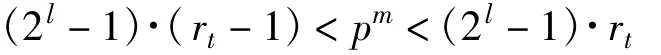
其中，l∈Z Z；rt为GF（2l）域中所有非零元素重复的周期数，不足一个周期的，记为一个周期，并计入rt中；rc是重复周期的带分数表示，整数部分表示重复的整数周期数，分数中分母表示一个周期的长度，分子表示不足一个周期的周期长度。l的取值与pm的值关系如下：

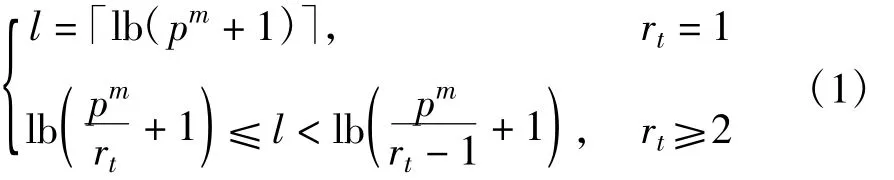
式中，l∈Z Z，「·表示向上取整。

令β是GF（2l）域的本原元。β-∞=0，β0=1，β，β2，…，β2l-2表示GF（2l）域中的所有元素，并且β2l-1=1。将基于BIBD区组的广义多进制位置向量定义为z（i）=（z0，z1，…，zpm-1），其向量取值对应的是GF（2l）域中的pm个非零元素，其中zi= βimod（2l-1），i∈Bi，而其它所有分量为0。Bi中的元素称为循环置换矩阵的位置数，决定着校验矩阵非零值的位置。因此，z（i）是GF（2l）域上的pm重向量，其重量为1。

令δ∈Bi且属于GF（pm）域中的元素，则广义多进制位置向量z（δ+1）定义为位置向量z（δ）向右循环移一位，第1列到第pm-1列的元素右移后乘以β，而最后一列元素则乘以βrt（2l-1）-（pm-1）后得到第1列元素。多进制位置向量z（δ+j）可定义为区组Bi中某一元素依次加非零值j∈GF（pm）后得到的一系列多进制位置向量。这样，在GF（2l）域上可形成以δ，δ+1，…，δ+pm-1的位置向量为行的多进制pm×pm大小的广义循环置换矩阵Qi，j。Qi，j可以认为是根据区组Bi中某一元素δ的二维pm重扩展：

二维pm重扩展是由垂直扩展和水平扩展两部分组成，对于某个元素δ，dispv（δ）=［δ，δ+1，…，δ+pm-1］T为该元素的垂直扩展，而disph（δ）=z（δ）为该元素的水平扩展。根据上述基本概念和提出规则，可以对基本区组Bi中所有元素进行广义二维pm重扩展得到广义多进制准循环矩阵。由于多进制校验矩阵非零值位置和数值的选取分别是建立在GF（pm）和GF（2l）这两个不同域中，构造出的二维pm重矩阵非零元素的分布具有两种情形：当rt=1时，在GF（2l）域上只具有部分域元素循环（rc＜1）或循环（rc=1）的特性；当rt≥2时，所有GF（2l）域非零元素个数一般在矩阵中分布不均，但是当2l-1=rcpm时，非零元素分布将是均匀的。

下面将阐述通过BIBD构造的基矩阵扩展到GF（2l）域多进制准循环校验矩阵的一般方法。假设通过BIBD方法构造出n×r的GF（pm）域下指数矩阵：

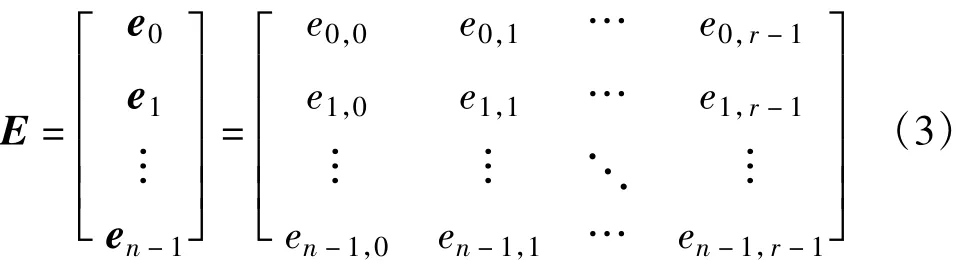
式中，ei，j∈GF（pm），E中的每一行是一个BIBD的基本区组。

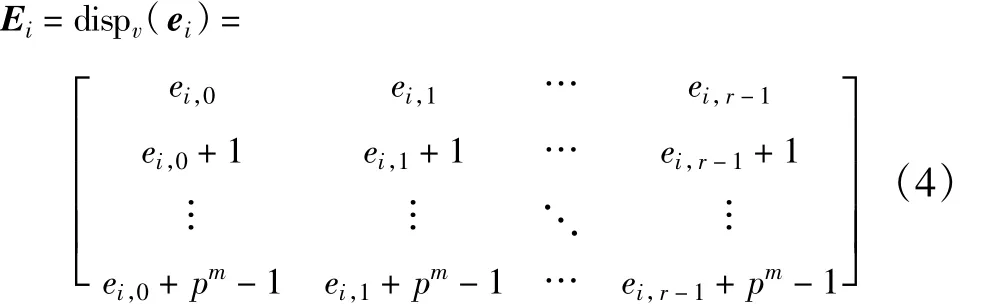
Ei具有如下的结构特性：每一列都是GF（pm）中循环顺序的pm个元素；任意两列所有位置的元素各不相同；任意两行所有位置的元素各不相同。根据这三点特性可知，来自不同两行垂直扩展的矩阵Ei和Ej不会在同一位置上具有相同的元素，这就保证了RC约束条件。然后将Ei进行水平扩展，就可构造出一个n×r阵列pm×pm循环置换矩阵Q：

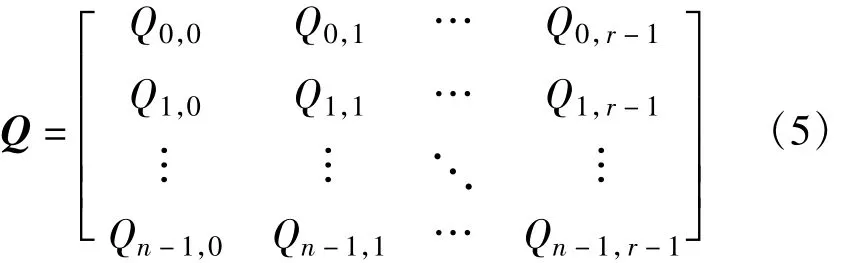
二维pm重扩展disp（ei，j）可以理解为将E中的一个元素ei，j扩展成一个循环置换矩阵Qi，j，对于任一整数对（dv，dc），其中1≤dv≤n，1≤dc≤r，令Q（dv，dc）是Q的dv×dc子阵列，则Q（dv，dc）就是一个GF（2l）域上的dvpm×dcpm矩阵，同时也满足RC约束，其零空间给出的就是长度为dcpm的多进制CPM-BIBD-LDPC码。其码率至少为1-dv／dc，girth至少为6。令H=QT，则H是一个r×n阵列pm×pm循环置换矩阵。对于任一整数对（dv，dc），其中1≤dv≤r，1≤dc≤n，令H（dv，dc）是H的dv×dc子阵列，则H（dv，dc）同样可表述为一个GF（2l）域上的dvpm×dcpm矩阵，同时也满足RC约束，其零空间给出的就是长度为dcpm的多进制CPM -BIBD-LDPC码。其行重为dc，列重为dv，码率至少为1-dv／dc，H满足RC约束，因此，girth至少也为6。

3 BIBD循环置换矩阵多进制LDPC码

3.1 第1类CPM-BIBD-LDPC码

令t是满足12t+1=pm的一个正整数，其中p是一个素数，m是一个正整数，也就是说，12t+1是一个素数的幂。假设GF（12t+1）域有一个本原元α满足α4t-1=αc，其中c是一个小于pm的正奇数，表1给出了部分t、12t+1及所对应的全部α和c的取值表，以使在素域GF（12t+1）中存在满足α4t-1=αc的本原元α，其中本原元α是用实数来表示的。

表1 在素域GF（12t+1）中本原元α满足α4t-1=αc时参数的取值Table 1 A listof parameters that the prime field GF（12t+1）has a primitive elementαsuch that the conditionα4t-1=αcholds

于是，对于具有q=12 t+1个元素集合G中每个元素重复f=1次得到集合X，存在一个BIBD，它具有n=t（12 t+1）个区组，每个区组由r=4个元素组成，每个元素恰好在k=4 t个区组中出现，每个元素对恰好在λ=1个区组中出现。用GF（12 t+1）域的元素α-∞=0，α0=1，α，α2，…，α12t-1来表示集合X的12 t+1=pm个元素。于是，X的BIBD可由下述t个基本区组完全确定：

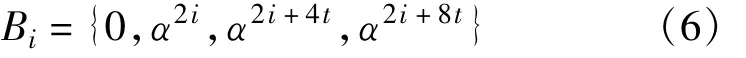
式中，0≤i＜t。

对于给定的第1类BIBD的每一个基本区组，可形成一个t×4的基矩阵E（1）：

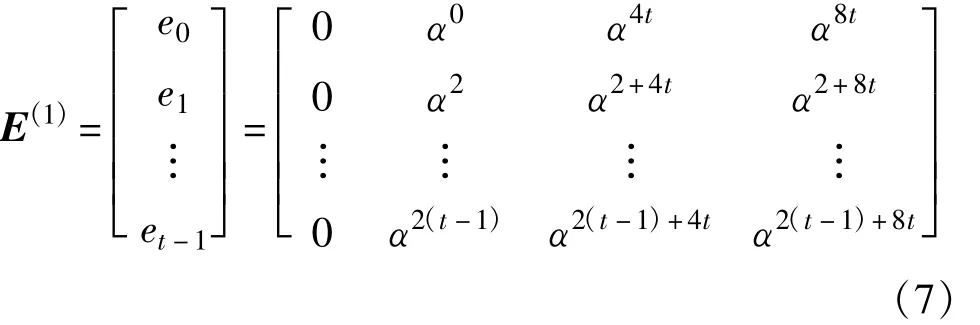
通过广义二维12t+1重扩展后可得多进制的（12t+1）×（12t+1）广义循环置换矩阵的t×4阵列：

可以很清楚地看出，Q（1）和H（1）分别是具有（12 t+1）×（12 t+1）的多进制循环置换矩阵的t×4

和4×t阵列，对于每一个子矩阵Qj，i（Hi，j）都是（12 t+1）×（12 t+1）的多进制循环置换矩阵，行重（列重）和列重（行重）分别为4和t。由于对Q（1）（dv，dc）和H（1）（dv，dc）的分析是一致的，只是dv和dc的取值范围不同。下面以H（1）为例，对于1≤dv≤4，1≤dc≤t，令H（1）（dv，dc）是H（1）的dv×dc

子阵列，则H（1）（dv，dc）是dv（12 t+1）×dc（12 t+1）的多进制矩阵，dv、dc恰为矩阵的列重和行重，H（1）

（dv，dc）的零空间给出了一个（dv，dc）的规则多进制CPM-BIBD-LDPC码。码长为N=dc（12 t+1），最小距离至少为dv+1，码率至少为1-dv／dc。

3.2 第2类CPM-BIBD-LDPC码

令t是满足20 t+1=pm的一个正整数，其中p是一个素数。假设GF（20 t+1）域有一个本原元α满足α4t+1=αc，其中c是一个小于pm的正奇数。表2给出了部分t、20 t+1及所对应的全部α和c的取值表，以使在素域GF（20 t+1）中存在满足α4t-1=αc的本原元α。

表2 在素域GF（20t+1）中本原元α满足α4t+1=αc时参数的取值Table 2 A list of parameters that the prime field GF（20 t+1）has a primitive elementαsuch that the conditionα4t+1=αcholds

于是，对于具有q=20 t+1个元素的集合X，存在一个BIBD，它有n=t（20 t+1）个区组，每个区组由r=5个元素组成，每个元素恰好在k=5 t个区组中出现，每个元素对恰好在λ=1区组中出现。用GF（20 t+1）域的元素α-∞=0，α0=1，α，α2，…，α20t-1来表示集合X的20 t+1=pm个元素。于是，X的BIBD由下述t个基本区组完全确定：

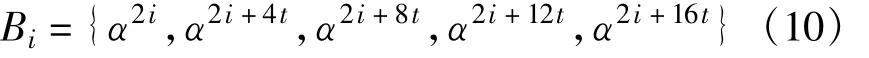
式中，0≤i＜t。

对于给定的第2类BIBD的每一个基本区组，可形成一个t×4的基矩阵E（2）：

E（2）的垂直扩展其实是通过将GF（pm）中的每个元素逐个加到这t个基本区组的每一个上而得到BIBD的所有n=t（20 t+1）个区组。通过广义二维20 t+1重扩展后可得到具有（20 t+1）×（20 t+1）广义多进制循环置换矩阵的t×5阵列Q（2），令H（2）=

［Q（2）］T，Q（2）和H（2）都可作为多进制LDPC码的校验矩阵。同样，对于H（2），1≤dv≤5，1≤dc≤t，而对于Q（2），1≤dv≤t，1≤dc≤5，H（2）（dv，dc）和Q（2）（dv，dc）分别是H（2）和Q（2）中dv×dc大小的子阵列，其零空间也给出了一个（dv，dc）的规则多进制CPM-BIBD-LDPC码。码长为N=dc（20 t+1），最小距离至少为dv+1，码率至少为1-dv／dc。

4 仿真结果及性能分析

本节给出两类由BIBD构造出的多进制CPMBIBD-LDPC码采用FFT-QSPA译码时的性能，并与相同比特长度的RS码和多进制Mackay LDPC码进行比较。所有仿真中的信号均采用BPSK调制，且在双边功率谱密度为N0／2的加性高斯白噪声（Additive White Gaussian Noise，AWGN）信道中传输。FFT-QSPA算法的最大迭代次数设置为50。

对于第1类多进制CPM-BIBD-LDPC码，取t =6，该设计具有如下参数：v=q=73，n=438，r= 4，k=48和λ=1，这样可以得到一个6×4的基矩阵E（1）。为了设计一列重dv=3、行重dc=6的多进制LDPC码，首先只取E（1）中的前6×3矩阵作为构造多进制CPM-BIBD-LDPC码的基矩阵E（1）（3，6）：

对E（1）（3，6）进行广义二维扩展的矩阵经转置后可得H（1）（3，6），它是一个由3×6的73×73的广义循环置换矩阵所构成校验矩阵，其非零值的位置和数值分别建立在GF（73）和GF（27）域上。由构造出的H（1）（3，6）的零空间将给出一个码率为0.504 6

的128-ary（438，221）CPM-BIBD-LDPC码。采用FFT-QSPA译码算法，该码的性能如图1所示。为了便于比较，我们也给出了同比特长度RS码的BM算法的误码性能。在FER为10-4处，相对于GF（29）

域上采用BM算法的（340，172）RS码来说，取得了大约3.80 dB的编码增益。

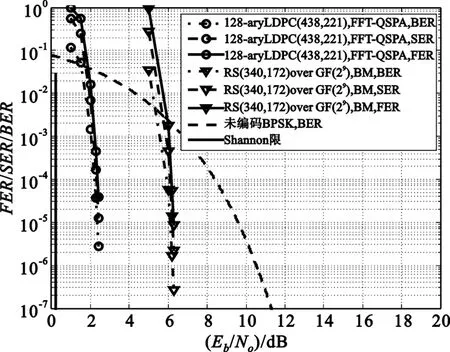
图1 采用FFT-QSPA译码的128-ary（438，221）CPM-BIBDLDPC码和采用BM算法GF（29）域的（340，172）RS码的误码性能Fig.1 Error performances of the 128-ary（438，221）BIBD-QCLDPC code decoded with the FFT-QSPA and the（340，172）RS code over GF（29）decoded with the BM algorithm

为了构造出不同的2l进制的LDPC码，根据式。因此，可以据此构造出128-ary、64-ary、32-ary CPM-BIBD -LDPC码。如图2所示，首先我们将128-ary CPM -BIBD-LDPC码与几乎同码率的128-ary Mackay LDPC码作一比较，相比于Mackay LDPC码，在FER为10-4处取得了大约0.14 dB的编码增益，因而本文提出的多进制CPM-BIBD-LDPC码具有更好的误码性能。通过对不同进制的LDPC码比较可以看出，随着进制数的减少，误码性能也相对变好，但是这种性能的差距不大，进制数的减少同时也能降低译码的复杂度。这种现象Mackay也曾指出［19］：随着域阶数的增加，其误码性能并不总是单调提升，这一现象的产生与校验矩阵的构造密切相关。

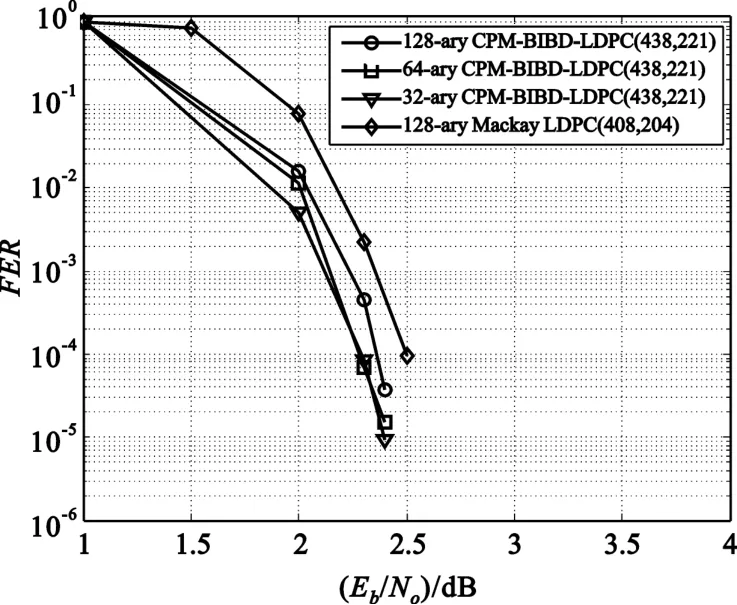
图2不同进制数下的（438，221）CPM-BIBD-LDPC码和128-ary Mackay LDPC码的性能比较Fig.2 Performances comparison of（438，221）CPM-BIBD-LDPC codes over different Galois fields and a 128-ary Mackay LDPC code

图3 给出了4种LDPC码的平均迭代次数曲线图，其反映了如下3点：构造出的多进制LDPC码具有很好的收敛特性；随着进制数的减少，其收敛越快，但是之间的差距并不大；相比于Mackay LDPC码，本文构造的LDPC码误码性能和收敛特性更为优越。

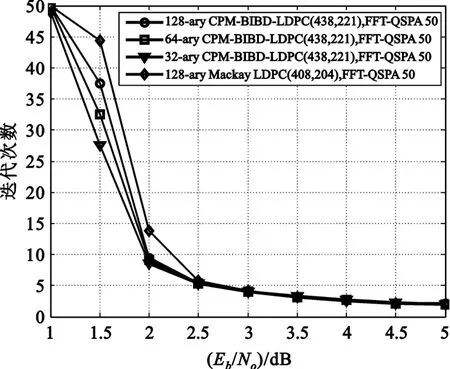
图3 采用FFT-QSPA译码不同进制数下CPM-BIBDLDPC码和Mackay LDPC码的平均迭代次数Fig.3 Average numbers of iterations for decoding CPM-BIBD-LDPC codes over different Galois fields and a Mackay LDPC code with the FFT-QSPA

对于第2类多进制CPM-BIBD-LDPC码，取t =3，这样可以得到一个3×5的基矩阵E（2）：

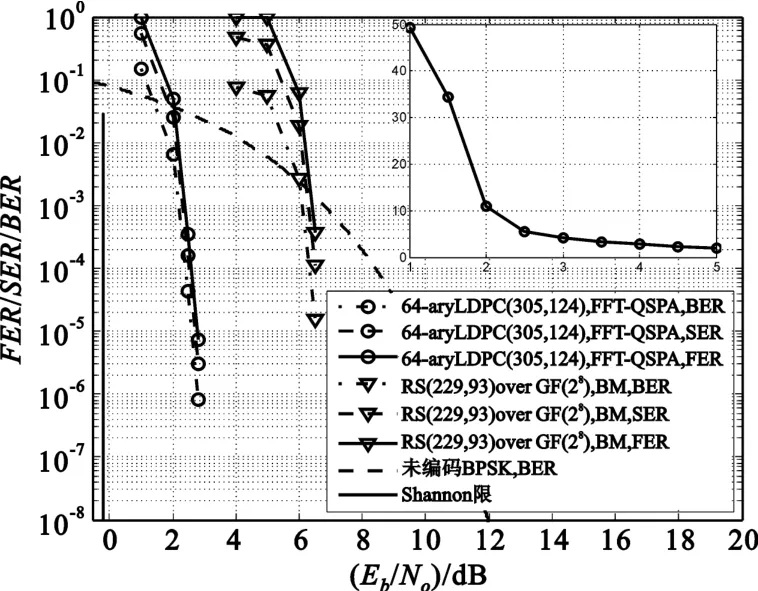
利用第2节提出的二维扩展方法可设计出一个183×305的多进制校验矩阵Q（2）（3，5），其列重和行重分别是3和5。Q（2）（3，5）的零空间给出一个码率为0.406 6的64-ary（305，124）CPM-BIBD-LDPC码。该LDPC码的FFT-QSPA和RS码的BM算法的误码性能和迭代性能如图4所示。与上述分析类似，在BER为10-4处，相对于GF（28）上采用BM算法的（229，93）RS码来说，取得了大约3.90 dB的编码增益。

5 结束语

多进制码的优势在于应对突发噪声和混合类型噪声比二进制码更为有效，多进制码中的RS码广泛应用于随机噪声、突发噪声和干扰同时存在的通信系统或数据存储系统中，而目前多进制LDPC码的研究呈现上升趋势，表现出了具有替代RS码的潜能。本文提出了基于BIBD循环置换矩阵的多进制LDPC码构造方法，多进制校验矩阵中非零元素位置的确定源于对基本区组的选择，而非零元素数值的选取则是建立在提出的广义多进制位置向量的基础上。在这种规则下构造出的多进制LDPC码具有QC特性，编译码复杂度低，其Tanner图没有长度为4的环路，提出的构造方法可适用于所有素数大小的循环置换子矩阵组成的多进制校验矩阵，具有很大的灵活性和可扩展性。仿真结果表明，在采用低复杂度FFT-QSPA译码时具有很好的纠错性能和良好的收敛特性，在几乎相同的比特长度上，本文构造的多进制LDPC码比RS码和多进制Mackay LDPC码具有更好的性能。

［1］Bose RC.On the construction of balanced incomplete design［J］.Annals of Eugenics，1939，9（1）：353-399.

［2］Ammar B，Honary B，Kou Y，et al.Construction of lowdensity parity-check codes based on balanced incomplete block designs［J］.IEEE Transactions on Information Theory，2004，50（6）：1257-1268.

［3］Lan L，Tai Y Y，Lin S，et al.New constructions of quasicyclic LDPC codes based on special classes of BIBD′s for the AWGN and binary erasure channels［J］.IEEE Transactions on Communications，2008，56（1）：39-48.

［4］Zhou B，Kang J，Song S，etal.Construction of non-binary quasi-cyclic LDPC codes by arrays and array dispersions［J］.IEEE Transactions on Communications，2009，57（6）：1652-1662.

［5］Chen C，Bai B，Wang X.Construction of nonbinary quasicyclic LDPC cycle codes based on singer perfect difference set［J］.IEEECommunications Letters，2010，14（2）：181-183.

［6］Kang J，Huang Q，Zhang L，et al.Quasi-cyclic LDPC codes：An algebraic construction［J］.IEEE Transactions on Communications，2010，58（5）：1383-1396.

［7］Chen X，Men A，Yang B，etal.Construction of LDPC codes over GF（q）withmodified progressive edge growth［J］.Journal of China Universities of Posts and Telecommunications，2009，16（5）：103-106.

［8］Shebl S，El-Fishawy N，Elazm A A，etal.A random construction of LDPC codes using a sub-optimal search algorithm［C］／／Proceedings of2009 National Conference on National Radio Science.New Cairo，Egypt：IEEE，2009：1-10.

［9］Li Z，Chen L，Zeng L，et al.Efficient encoding of quasicyclic low-density parity-check codes［J］.IEEE Transactions on Communications，2006，54（1）：71-81.

［10］Song S，Zhou B，Lin S，et al.A unified approach to the construction of binary and nonbinary quasi-cyclic LDPC codes based on finite fields［J］.IEEE Transactions on Communications，2009，57（1）：84-93.

［11］Barnault L，Declercq D.Fast decoding algorithm for LDPC over GF（2q）［C］／／Proceedings of 2003 IEEE Information TheoryWorkshop.Paris，France：IEEE，2003：70-73.

［12］Kou Y，Lin S，Fossorier M P C.Low-density paritycheck codes based on finite geometries：A rediscovery and new results［J］.IEEE Transactions on Information Theory，2001，47（7）：2711-2736.

［13］Lan L，Zeng L，Tai Y Y，et al.Construction of quasicyclic LDPC codes for AWGN and binary erasure channels： A finite field approach［J］.IEEE Transactions on Information Theory，2007，53（7）：2429-2458.

［14］FossorierM PC.Quasi-cyclic low-density parity-check codes from circulant permutationmatrices［J］.IEEE Transactions on Information Theory，2004，50（8）：1788-1793.

［15］Djordjevic IB.Quantum LDPC codes from balanced incomplete block designs［J］.IEEE Communications Letters，2008，12（5）：389-391.

［16］Zeng L，Lan L，Tai Y Y，et al.Construction of nonbinary cyclic，quasi-cyclic and regular LDPC codes：A finite geometry approach［J］.IEEE Transactions on Communications，2008，56（3）：378-387.

［17］Zeng L，Lan L，Tai Y Y，et al.Constructions of nonbinary quasi-cyclic LDPC codes：A finite field approach［J］.IEEE Transactions on Communications，2008，56（4）：545-554.

［18］Voicila A，Declercq D，Verdier F，et al.Low-complexity decoding for non-binary LDPC codes in high order fields［J］.IEEE Transactionson Communications，2010，58（5）：1365-1375.

［19］Davey M C，MacKay D.Low-density parity check codes overGF（q）［J］.IEEE Communications Letters，1998，2（6）：165-167.

LIUBing was born in Nanchang，Jiangxi Province，in 1984. He is now an engineer with the Ph.D.degree.His research interests include error control coding and signal processing for digital communications.

Email：liubing5275093＠hotmail.com

陶伟（1974—），男，黑龙江哈尔滨人，博士研究生，工程师，主要研究方向为差错控制编码和无线数据传输；

TAO Wei was born in Harbin，Heilongjiang Province，in 1974.He is now an engineer and currently working toward the Ph.D.degree.His research interests include error control coding and wireless data transmission.

Email：alantao0451＠yahoo.com.cn

窦高奇（1981—），男，山西长治人，博士，讲师，主要研究方向为差错控制编码和数字通信信号处理；

DOU Gao-qi was born in Changzhi，Shanxi Province，in 1981.He is now a lecturer with the Ph.D.degree.His research interests include error control coding and signal processing for digital communications.

Email：gqdou0917＠163.com

高俊（1957—），男，江苏泰兴人，1989年获博士学位，现为教授、博士生导师，主要研究方向为信道编码和数字通信。

GAO Jun wasborn in Taixing，Jiangsu Province，in 1957.He received the Ph.D.degree from Beijing Institute of Technology in 1989. He is now a professor and also the Ph.D.supervisor.His research interests include error control coding and digital communications.

Email：gaojunnj＠163.com

Construction of Nonbinary LDPC Codes Based on BIBD Circulant Perm utation M atrices

LIU Bing1，3，TAOWei2，3，DOU Gao-qi3，GAO Jun3
（1.Unit91469 of PLA，Beijing 100841，China；2.Naval Academy of Armament，Beijing 100161，China；3.College of Electronic Engineering，Naval University of Engineering，Wuhan 430033，China）

The algebraic method for constructing nonbinary quasi-cyclic（QC）low-density parity-check（LDPC）codes based on balanced incomplete block designs（BIBD）is presented.The generalized nonbinary location vector is proposed on constructions.A nonbinary matrix，which consists of nonbinary circulant submatrices，is formed by generalized two-dimensionalmatrix dispersion considering the generalized nonbinary location vector and BIBDmethod.The codes constructed by thismethod have girths at least6.Experimental results show that significant coding gains are achieved over Reed-Solomon codes of the same parameters under the AdditiveWhite Gaussian Noise（AWGN）channel with iterative decoding Fast Fourier Transform based q-ary Sum-Product Algorithm（FFT-QSPA）.And a good performance is also achieved over nonbinary Mackay LDPC codes with almost the same conditions.

nonbinary low-density parity-check（LDPC）codes；quasi-cyclic；balanced incomplete block design；generalized nonbinary location vector；two-dimensional dispersion

The National High-tech R＆D Program of China（863 Program）（2009AAJ128，2010AA7010422）；The National Science Foundation for Post-doctoral Scientists of China（200902671）

TN911.22

A

10.3969／j.issn.1001-893x.2011.09.006

刘冰（1984—），男，江西南昌人，博士，工程师，主要研究方向为差错控制编码和数字通信信号处理；

1001-893X（2011）09-0027-08

2011-02-18；

2011-08-30

国家高技术研究发展计划（863计划）项目（2009AAJ128，2010AA7010422）；国家博士后科学基金（200902671）