基于容量最大化的多用户MIMO-OFDM子载波分配算法✴

管张均，周希朗

（上海交通大学电子工程系，上海200240）

基于容量最大化的多用户MIMO-OFDM子载波分配算法✴

管张均，周希朗

（上海交通大学电子工程系，上海200240）

针对多用户MIMO-OFDM通信网络，提出了一种基于系统和容量最大化的子载波分配算法。通过对MIMO-OFDM系统和容量公式进行分析，提取出子载波分配的判决参数，再利用匈牙利算法对子载波进行分配，同时分析了分配后系统平均容量的统计特性。为了兼顾公平，又提出了传输速率最小的用户传输速率最大化的子载波分配算法。仿真结果表明，所提容量最大化算法能使系统和容量达到全局最大值，且具有较低的复杂度。

MIMO-OFDM；子载波分配；匈牙利算法；容量最大化

1 引言

多输入多输出技术（MIMO）利用收发两端配置多根天线来获得空间分集增益，以提高系统性能和频谱效率［1-2］。正交频分复用技术（OFDM）把整个传输频带划分为多个相互正交的子载波，把频率选择性衰落信道转变为若干个平坦衰落子信道，从而解决了多径衰落的问题［3-4］。因此，这两种技术的结合（MIMO-OFDM）就成为未来无线通信网络极富前景的候选技术。

在MIMO-OFDM系统中，子载波分配是比较热门的一个问题。根据优化目标的不同，动态子载波分配主要划分为两大类［5-7］：一是在给定用户传输速率或误码率下，最小化基站发射功率；二是在给定发射功率下，最大化系统和容量。通常这些优化问题都是非凸和计算复杂度极高的。

文献［6］证明，当每一个子载波都分配给其上信道状况最好的用户时，系统容量可以达到最大。但是文献［6］并没有考虑公平性的问题，当信道状况变化剧烈时，那些信道处于深度衰落的用户几乎得不到任何通信资源。

本文提出了一种基于系统和容量最大化的自适应子载波分配算法。从MIMO-OFDM系统和容量公式中提取出子载波分配的判决参数，利用匈牙利算法对子载波进行分配。本文还提出了传输速率最小的用户（即最差用户）传输速率最大化的子载波分配算法，即通过多次迭代，把空闲子载波分配给最差用户，使其传输速率有所上升，从而在系统和容量相对较大时能兼顾用户间的公平。

2 系统模型与子载波分配判决参数提取

多用户OFDM系统模型如图1所示。所有用户的信道状况信息通过信道估计模块传送到子载波分配模块，子载波分配模块利用某种算法对子载波进行分配。一旦用户的信道状况信息有所改变，子载波分配模块就要对子载波进行重新分配。

图1 多用户OFDM系统框图Fig.1 Block diagram ofmultiuser OFDM system

我们试图根据MIMO-OFDM系统的和容量公式得到一个单变量来表征用户信道矩阵的状况，供子载波分配模块作判决参数。基于MIMO-OFDM的系统瞬时和容量可以表示为［8］

式中，K为用户总数，N为总的子载波数，N0是加性白高斯噪声（AWGN）的功率谱密度，B是总的带宽，pk，n是分配给用户k在子载波n上的功率，Hk，n是用户k在子载波n上的信道状况矩阵；ρk，n可以为0或1，表明子载波n是否被用户k占用，这说明每个子载波被一个用户独占；NR和NT分别为用户和基站端的天线数，M=min（NR，NT）；λk，n，i是矩阵Hk，nHHk，n的第i个特征值。

根据Jensen不等式

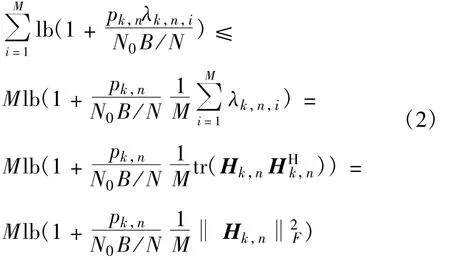
我们可以看出，Hk，n的Frobenius范数可以表征用户k在子载波n上的信道矩阵的状况，因此可以把子载波n分配给其上信道矩阵Frobenius范数最大的用户。

当考虑高信噪比（SNR）的情况时，式（2）的左边可以重写为

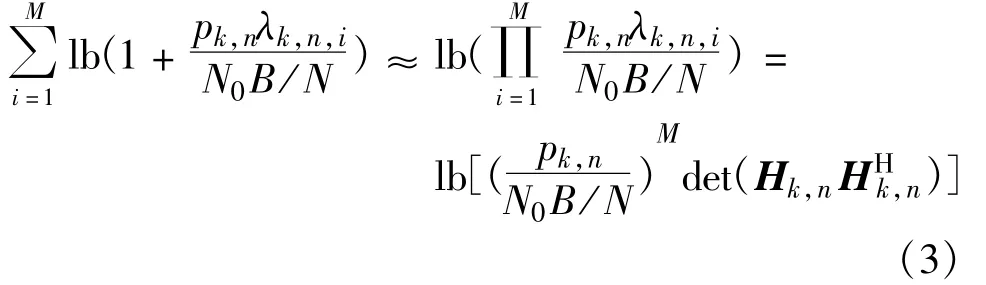
所以在高信噪比下，可以把子载波n分配给其上Hk，nHHk，n行列式的值最大的用户。利用匈牙利算法可以对子载波进行分配。

3 系统平均容量的统计特性分析

由随机变量的理论可知，‖Hk，n‖2F是一个自由度为2NTNR的Chi-square分布随机变量，其概率密度函数（PDF）为

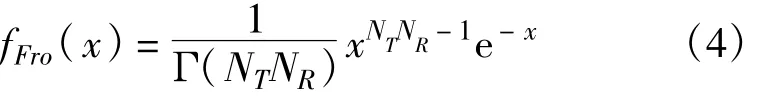
式中，Γ（NTNR）是Gamma函数，Γ（NTNR）=（NTNR-1）！。

相应的累积分布函数（CDF）为

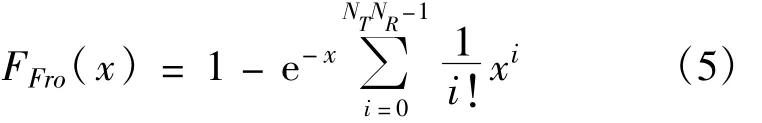
通过排序统计，我们得到在K个用户间进行自适应子载波分配之后，子载波n上的瞬时信道容量的累积分布函数可以表示为

4 最差用户容量最大化的子载波分配算法

我们在推导上述子载波分配算法时，都是以MIMO-OFDM系统和容量最大化为目标的，但是这样用户间的公平性得不到保障。实际上，我们可以很容易地将第2节给出的判决参数应用于最差用户容量最大化的子载波分配算法中去。具体的子载波分配算法如下。

（1）初始化：令Ck=0，其中k=1，2，…，K，集合A=｛1，2，…，N｝。

（2）for k=1：K，对于所有的子载波j∈A，寻找满足βk，n＞βk，j的子载波n。

更新Ck和A：Ck=C（βk，n），A=A-｛n｝。

（3）while A≠Ø，对于所有的用户i（1≤i≤K），寻找满足Ck＜Ci的用户k。对于上述用户k，在所有的子载波j∈A中寻找满足βk，n＞βk，j的子载波n。

更新Ck和A：Ck=Ck+C（βk，n），A=A-｛n｝式中，Ck是用户k当前的瞬时容量，βk，n是判决用户k能否占用子载波n的参数。利用第2节得到的判决参数即可对子载波进行相应的分配。

5 仿真结果

在仿真中，基站的发射功率为1W，加性白高斯噪声的功率谱密度为-80 dBW／Hz；总的带宽为1 MHz，被划分为64个子载波；发射天线数为3，接收天线数为2。

图2给出了不同判决参数下系统和容量随用户数的变化曲线。从图中可以看出，由于匈牙利算法是全局优化算法，所以其容量始终优于最差用户容量最大化算法。随着用户数的增加带来的多用户分集增益，两种算法的容量都呈上升趋势。

图3给出了不同判决参数下最差用户容量随用户数的变化曲线。从图中可以看出，由于匈牙利算法是全局优化算法，为了达到全局最优必然要牺牲掉一些信道状况不好的用户的利益。而最差用户容量最大化算法可以保证在系统容量相对较大的前提下，最差用户的容量也有所提升，从而兼顾了公平性的问题。

图4和图5分别给出了在第一种判决参数下系统平均容量的累积分布函数随用户数和天线数的变化曲线。从图4可以看出，仿真曲线和通过式（6）得到的解析曲线拟合得很好，这也验证了理论推导的正确性。随着用户数的增加，系统平均容量也会因为多用户分集增益有所提升。从图5中除了可以看出由多用户分集增益带来的系统容量提升外，还可以看到由于收发天线数的增加，由空间分集增益带来的系统平均容量提升。

图2 系统和容量与用户数的关系图Fig.2 System sum capacity versus numbers of users

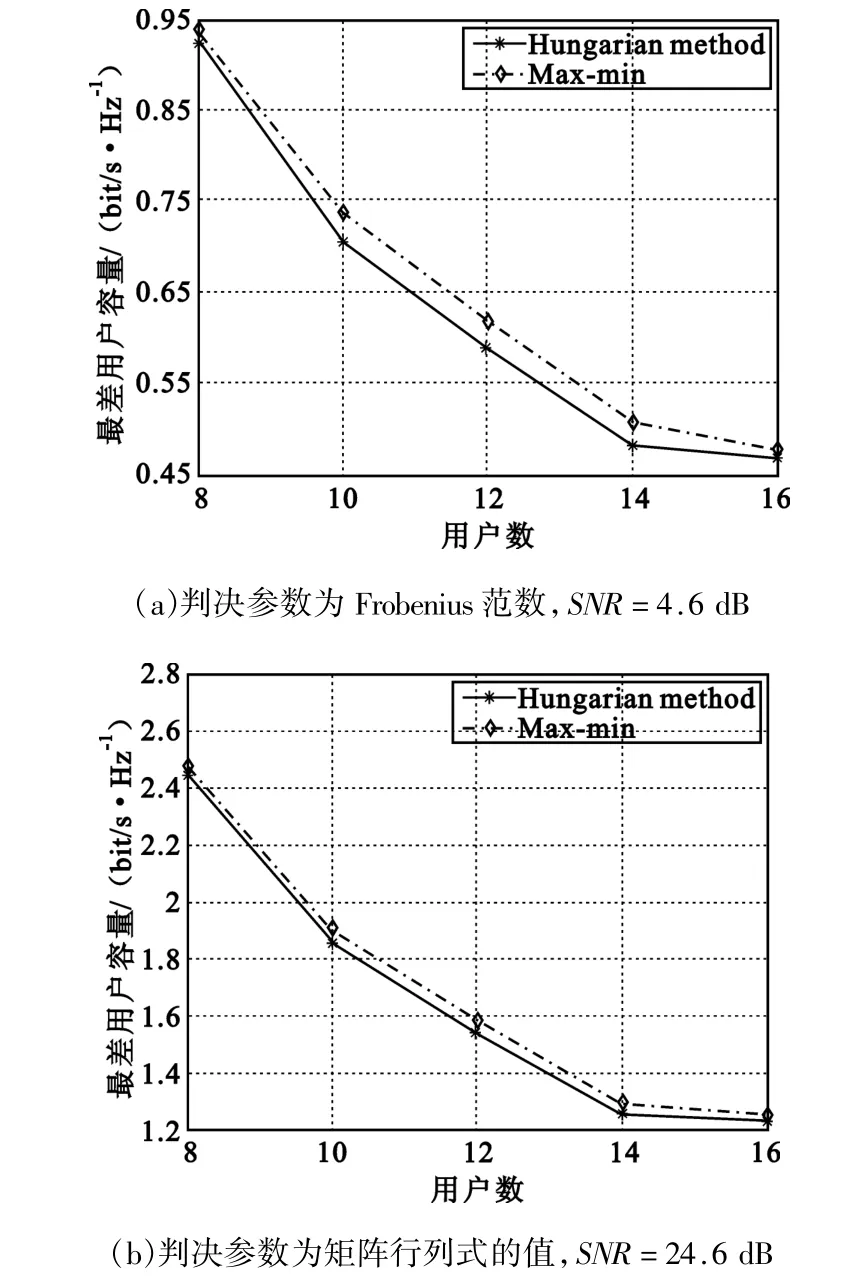
图3 最差用户容量与用户数的关系图Fig.3 Capacity of the worst user versus numbers of users

图4 系统平均容量的累积分布函数与用户数的关系图（判决参数为Frobenius范数，SNR=4.6 dB）Fig.4 CDF of system average capacity versus numbers of users（Frobenius-norm，SNR=4.6 dB）

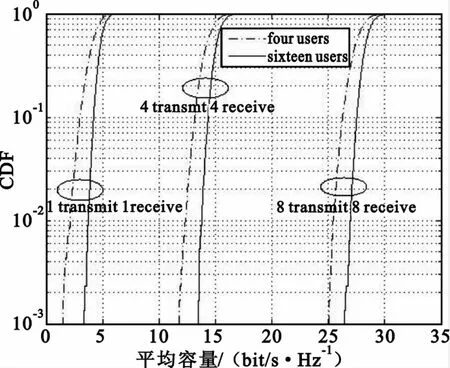
图5 系统平均容量的累积分布函数与天线数的关系图（判决参数为Frobenius范数，SNR=4.6 dB）Fig.5 CDF of system average capacity versus numbers of antennas（Frobenius-norm，SNR=4.6 dB）

6 总结

本文提出了一种基于系统和容量最大化的自适应子载波分配算法。从实验结果来看，该算法能使系统和容量达到全局最大值。为了兼顾公平，本文还提出了最差用户传输速率最大化的子载波分配算法。本文提出的子载波分配算法对无线通信系统的资源分配具有一定的参考价值。下一步将针对目前较为热门的中继通信网络，利用两跳或多跳之间信道衰落的变化，研究相应的子载波分配算法。

［1］Adarsh B.Narasimhamurthy，Cihan Tedepelenlioglu.Antenna Selection for MIMO-OFDM SystemsWith Channel Estimation Error［J］.IEEE Transactions on Vehicular Technology，2009，58（5）：2269-2278.

［2］Sébastien Simoens，Olga Muñoz-Medina，Josep Vidal，etal. Compress-and-Forward Cooperative MIMO RelayingWith Full Channel State Information［J］.IEEE Transactions on Signal Processing，2010，58（2）：781-791.

［3］Tevfik Yücek，Hüseyin Arslan.MMSE noise plus interference power estimation in adaptive OFDM systems［J］.IEEE Transactions on Vehicular Technology，2007，56（6）：3857-3863.

［4］李富年，朱光喜，王德胜.OFDM协作通信中的机会中继和功率分配算法［J］.华中科技大学学报（自然科学版），2010，28（9）：14-17. LIFu-nian，ZHU Guang-xi，WANG De-sheng.Opportunistic relay and power allocation optimization in cooperative OFDM networks［J］.Journal of Huazhong University of Science and Technology（Natural Science Edition），2010，28（9）：14-17.（in Chinese）

［5］Wong C Y，Cheng R S，Letaief K B，et al.Multicarrier OFDM with adaptive subcarrier，bit，and power allocation［J］.IEEE Journal on Selected Areas in Communications，1999，17（10）：1747-1758.

［6］Jang J，Lee K B.Transmit power adaptation for multiuser OFDM systems［J］.IEEE Journal on Selected Areas in Communications，2003，21（2）：171-178.

［7］Zukang Shen，Jeffrey G.Andrews，Brian L.Evans.Adaptive Resource Allocation in Multiuser OFDM Systems With Proportional Rate Constraints［J］.IEEE Transactions on Wireless Communications，2005，4（6）：2726-2737.

［8］Bolckei H，Gesbert D，Paulraj A J.On the capacity of OFDM-based spatial multiplexing systems［J］.IEEE Transactions on Communications，2002，50（2）：225-234.

GUAN Zhang-jun was born in Nantong，Jiangsu Province，in 1981.He received the M.S.degree from Nanjing Research Institute of Electronic Technology in 2006.He is now a graduate student. His research concernswireless communication techniques.

Email：guan-zhangjun＠sjtu.edu.cn

周希朗（1952—），男，江苏徐州人，教授、博士生导师，主要研究方向为微波、毫米波集成电路。

ZHOU Xi-lang was born in Xuzhou，Jiangsu Province，in 1952. He is now a professor and also the Ph.D.supervisor.His research interests includemicrowave andmillimeter wave integrated circuits.

Email：xlzhou＠sjtu.edu.cn

Subcarrier Allocation Algorithm s for M ultiuser M IMO-OFDM Systems Based on M aximum of Capacity

GUAN Zhang-jun，ZHOU Xi-lang
（Department of Electronic Engineering，Shanghai Jiaotong University，Shanghai200240，China）

A subcarrier allocation algorithm is presented formultiuser MIMO-OFDM communication network based onmaximum of the system sum capacity.Judging parametersof subcarrier allocation are extracted from the capacity formulas，and subcarriers are allocated by Hungarianmethod.The statistical characteristic of the system average capacity is also analysed.For fairness concerning，another subcarrier allocation algorithm is proposed to maximize theminimum user′s rate.Simulation results show that the proposed algorithm tomaximize the system sum capacity is globally optimal and easy to implement，and also has low complexity.

MIMO-OFDM；subcarrier allocation；Hungarianmethod；maximum of capacity

TN929.5

A

10.3969／j.issn.1001-893x.2011.09.026

管张均（1981—），男，江苏南通人，2006年获南京电子技术研究所电磁场与微波技术专业硕士学位，现为上海交通大学电子工程系博士研究生，主要研究领域为无线通信技术；

1001-893X（2011）09-0127-04

2011-06-20；

2011-07-27