基于小波变换变步长LMS自适应信道均衡的新方法✴

王丹，杨雷，普杰信

（河南科技大学电子信息工程学院，河南洛阳471003）

基于小波变换变步长LMS自适应信道均衡的新方法✴

王丹，杨雷，普杰信

（河南科技大学电子信息工程学院，河南洛阳471003）

结合变换域最小均方（LMS）和变步长LMS算法的优势，提出了一种基于小波变换的变步长LMS自适应均衡方法。该方法中步长调整函数采用了改进的Sigmoid函数，该函数具有简单且误差信号接近零时变化缓慢的特点。并且，在训练模式、判决引导模式以及混合模式下，将提出方法和传统均衡方法进行了仿真比较。结果表明，所提出的方法比传统的线性LMS算法、变步长LMS以及小波变换LMS收敛更快、性能更优。

自适应信道均衡；线性均衡；LMS算法；变步长；小波变换

1 引言

在数字通信系统中，由于传输环境的不理想，接收到的数据流所产生的码间干扰（ISI）是限制系统在带限信道上进行高速数据传输的主要干扰源。因此，需要接收端采用自适应均衡来补偿时变信道参数变化所引起的信号畸变，减小误码，提高通信质量。目前，均衡器可以分为线性均衡器和非线性均衡器［1］。如果信道畸变不是很严重，采用线性均衡器（Linear Equalizer，LE）结构能取得较好的效果，但不适合信道深度衰落的场合。非线性的判决反馈均衡器（Decision Feedback Equalizer，DFE）［1］能抑制强ISI，其抗干扰能力比LE好，但DFE存在误差传播问题，一次误判可能影响后面若干个判决的正确性，且复杂度较高。

近年来，由于基于最小均方（Least Mean Square，LMS）算法［1］简单、数值稳定、易于实现和计算量小，所以广泛地用于自适应滤波器系数的调整。然而，若输入信号自相关矩阵的条件数较大，那么算法收敛速度将下降，跟踪性能将受到影响。而且，固定步长因子无法解决收敛速度和稳态误差之间的矛盾。递归最小二乘（Recursive Least Squares，RLS）［2］方法收敛速率较高，性能较好，且算法性能与输入信号特性无关，但其复杂度较高且存在数值稳定性的问题。

由于固定步长LMS算法对输入信号特性敏感性，并且步长的选取在收敛速度和稳态均方误差（MSE）之间存在矛盾，所以其改进方案可以分为变步长LMS［3-7］和变换域LMS［2，8，9］两大类。文献［3］提出了步长是误差信号Sigmoid函数的设想，该算法能同时获得较快的收敛速度、跟踪速度和较小的稳态误差。然而，该Sigmoid函数过于复杂，且在误差e（n）接近零处变化太大，不具有缓慢变化的特性，使得算法在自适应稳态阶段仍有较大的步长变化。针对这一缺点，文献［4］给出了另一种步长调整函数。该函数比Sigmoid函数简单，且在误差e（n）接近零处具有缓慢变化的特性，克服了Sigmoid函数在自适应稳态阶段步长调整过程中的不足。另一方面，通过对自适应均衡的输入信号进行正交变换，也可提高LMS算法收敛速度。由于小波变换具有较好的去相关能力和良好的时频特性，并且复杂度较低，所以小波理论的出现为变换域自适应滤波开辟了新的思路［2，8］。

本文通过同时利用变步长LMS算法［4］和变换域LMS算法［2，8］的优势，提出了一种基于小波变换变步长LMS自适应线性均衡方法（WTVSLMSLE）。仿真结果表明，与传统方法相比，提出的方法有更快的收敛速率。

本文内容安排如下：第2节给出基于自适应信道均衡的系统模型；第3节重点介绍了本文提出的WTVSLMSLE方法；第4节给出了仿真结果；最后是结论。

2 系统模型

图1给出了含有自适应信道均衡的数字通信系统框图。其中，等效信道冲激响应h（n）抽象地代表了发送滤波器、调制器、传输介质和解调器总体效应，其径数假设为L。数据a（n）是发送的随机信息序列，信道输出信号x（n）为

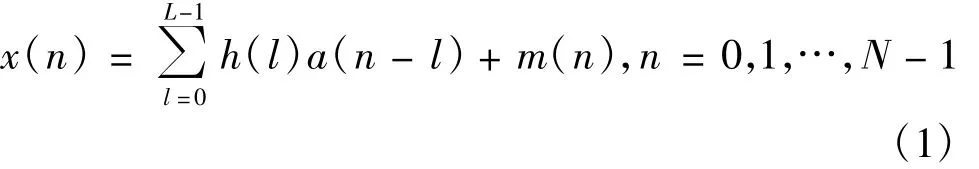
式中，m（n）表示均值为零、方差为σ2m的高斯白噪声。

图1 基于自适应信道均衡的数字通信系统框图Fig.1 Block diagram of a digital communication system using adaptive channel equalization

自适应均衡即是利用前一时刻获得的均衡器参数来自动调整当前时刻的均衡器参数，以适应信道中各个未知的或时变的统计特征，从而消除码间干扰。应用横向结构的滤波器形式来实现自适应滤波是最常用的一种方法。如果均衡器系数w（n）长为M，则可得均衡器的输出信号y（n）为

式中，均衡器系数w（n）的求解可类似于维纳滤波器时域解的求解方法，即使误差均方值最小的权系数为最小均方意义下的最佳值，如式（3）所示：

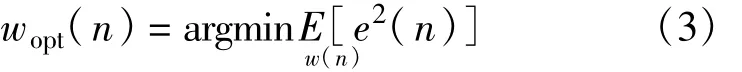
式中，e（n）=d（n）-y（n）是误差信号，d（n）为均衡器的期望信号。自适应模式大致可分为训练模式、判决引导模式和盲模式3种［4］。其中，判决引导模式一般跟训练模式相结合使用，在训练成功之后用判决引导算法来跟踪时变信道的变化，该模式为混合模式。在训练模式和判决引导模式下期望信号分别为

式中，tdelay表示由于信道传输引起的延时，取为fix（（M+L）／2）-L是比较合理的，以弥补信道和LE均衡器对信号引起的延时，其中fix表示取整函数。

3 提出的WTVSLMSLE方法

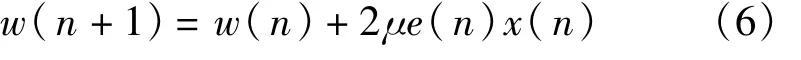
Widrow-Hoff LMS算法是求最佳权矢量的一个简单和有效的递推方法［8］，将其应用于LE问题的求解，其LE系数矢量迭代过程为式中，() x n为时刻n的LE均衡器输入信号矢量；μ为步长调整因子，它可以控制算法的稳定性和收敛速度，且有0＜μ＜1／λmax，λmax表示均衡器输入信号的自相关矩阵Rxx的最大特征值。算法的收敛性取决于矩阵Rxx的谱的特性，即矩阵Rxx的特征值扩展程度。

为了改善输入信号自相关矩阵的谱特性，可将输入信号进行正交小波变换，减小特征值扩散程度，提高算法收敛速度。另外，由于LMS算法的固定步长在收敛速度、跟踪速度与权失调噪声方面是相互矛盾的，因此若在小波变换域应用时变步长的LMS算法，则可以进一步改善均衡算法的性能。因此，本文方法结合小波正交变换和变步长调整的LMS方法对信道进行自适应均衡，框图如图2所示。

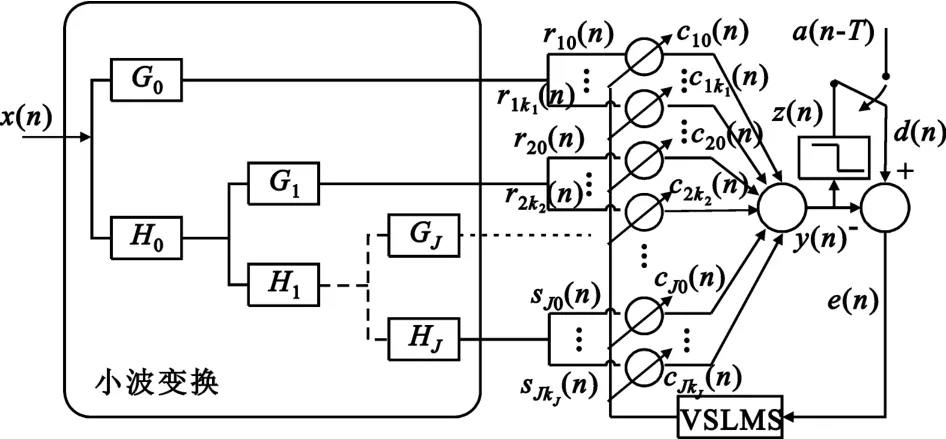
图2 提出的WTVSLMSLE方法框图Fig.2 Block diagram of the proposed WTVSLMSLEmethod

其具体实现步骤如下：

Step 1：对均衡器的输入信号x（n）进行小波变换r（n）=WTx（n），其中WT是小波变换矩阵，为

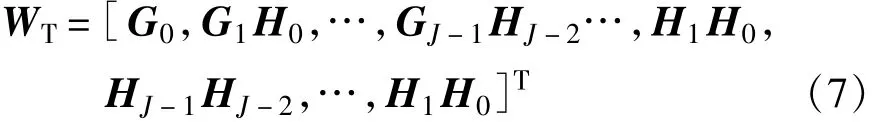
式中，Hj和Gj分别是由尺度滤波器和小波滤波器构成的矩阵，J为小波分解的最大分解尺度。

Step 2：计算均衡器输出信号y（n）=c（n）Tr（n），其中c（n）为小波变换后的均衡器系数矢量。

Step 3：计算均衡器的误差信号e（n）=d（n）-y（n）。

Step 4：由误差信号按照改进的Sigmoid函数［4］计算步长值，即：

式中，参数α＞0控制函数的形状，参数0＜β＜1／λmax控制函数的取值范围，exp（·）表示e指数操作。

Step 5：进行均衡器系数迭代计算，为

c（n+1）=c（n）+2μ（n）R-1（n）e（n）r（n）（9）

由于在变换域LMS算法中进行功率归一化可以改善收敛速率，所以，式（9）中的矩阵R() n是由经过小波变换后输入信号功率的估计值组成的对角阵，其对角向量为

式中，γ为控制估计精度和跟踪能力的平滑系数，取值范围为0＜γ＜1，一般取比较接近于1的值。

4 仿真与分析

本小节利用MATLAB仿真软件对经典RLS线性均衡（RLSLE）、经典LMS线性均衡（LMSLE）、变步长LMS线性均衡（VSLMSLE）、小波变换LMS线性均衡（WTLMSLE）算法以及提出的WTVSLMSLE算法收敛速度进行比较。仿真参数如表1所示。

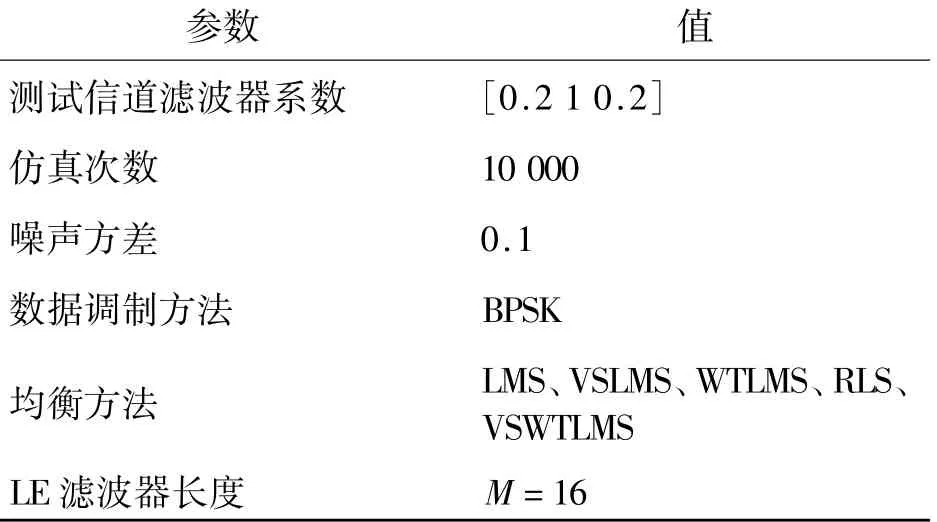
表1 仿真参数Table 1 The simulation parameters

仿真中自适应均衡算法参数的设置如表2所示。为了比较均衡算法的收敛速度，表2中参数的设置尽可能地满足相同均方误差水平，从而收敛速度可通过比较MSE首次低于平均MSE值的迭代次数来衡量。

表2 自适应算法参数Table 1 The parameters of adaptive algorithms

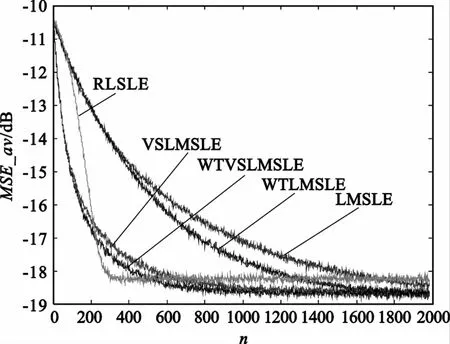
图4判决引导模式均衡算法收敛曲线比较Fig.4 Convergence rate of severalmethods in the decision-directedmode

图3 ～5分别给出了提出方法和传统方法在训练模式、判决引导模式以及混合模式下收敛曲线的比较结果。其中，在混合自适应模式中，当采样点数达到1 000时，均衡算法由训练模式转入判决引导模式。结果表明：在训练模式和混合模式下，WTLMSLE方法和VSLMSLE方法性能比较接近，且均优于经典LMSLE方法；在判决引导模式下，WTLMSLE方法略优于经典LMSLE方法，但远差于VSLMSLE方法的收敛性能；在3种自适应模式下，提出的WTVSLMSLE算法与RLS算法性能接近，收敛速度最快，而其它算法在相同的稳态误差条件下均劣于提出的WTVSLMSLE算法，这是由于所提出方法结合了变步长和小波变换域两者的优势，因此不论在哪种模式下都具有较快的收敛速度，均衡性能得到了进一步的提高。

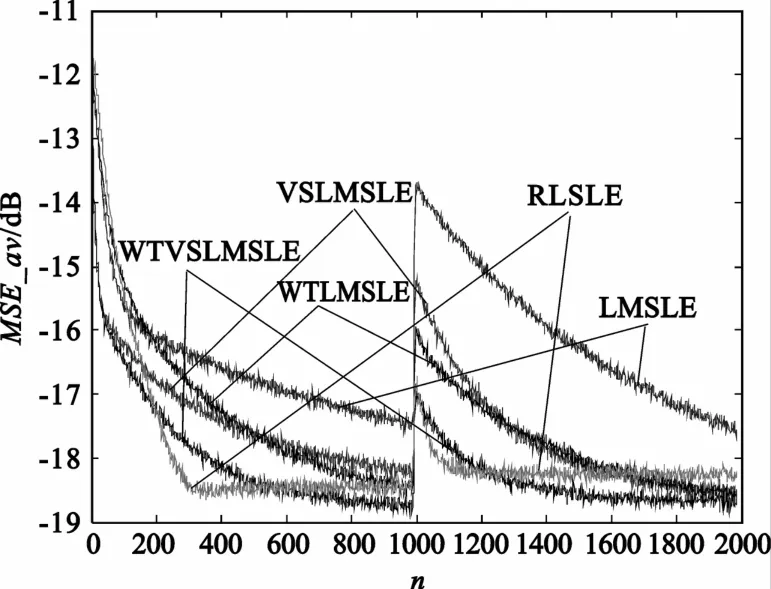
图5 混合模式下均衡算法收敛曲线比较Fig.5 Convergence rate of severalmethods in the hybridmode

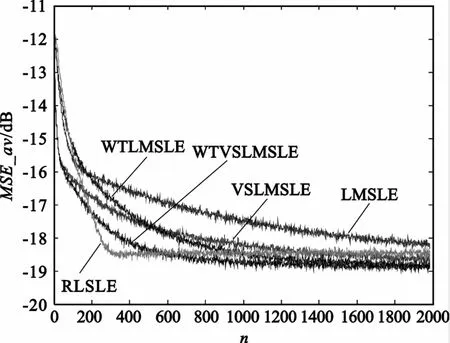
图3 训练模式下均衡算法收敛曲线比较Fig.3 Convergence rate of severalmethods in the trainingmode

5 结论

本文通过结合变步长LMS算法和变换域LMS算法的优势，提出了一种基于小波变换的改进Sigmoid函数变步长LMS线性均衡方法。与现有文献不同，本文在训练模式、判决引导模式及两者的混合模式下将所提方法与多种传统自适应均衡算法进行了仿真比较。结果表明：和传统的变步长LMS方法及小波变换域LMS方法相比，所提方法收敛速度更快，均衡性能更好。由于本文方法局限于线性均衡的范畴，所以仅适用于码间干扰比较弱的通信场合。本文进一步研究方向为分析信道突变对所提方法的影响，并将所提方法推广到适用于强码间干扰的非线性自适应均衡中。

［1］龚耀寰.自适应滤波［M］.北京：电子工业出版社，1989：12-28.GONGYao-huan.Adaptive filtering［M］.Beijing：Publishing House of Electronics Industray，1989：12-28.（in Chinese）

［2］Niu X.Research of discrete wavelet transform domain adaptive equalization algorithm［C］／／Proceedings of the 8th International Conference on Signal Processing.Beijing：IEEE，2006：1-6.

［3］贾景繁，欧阳景正.一种新的变步长LMS自适应滤波算法［J］.数据采集与处理，1997，12（3）：171-174. JIA Jing-fan，OUYANG Jing-zheng.A novel variable step size LMS adaptive filtering algorithm based on sigmoid function［J］.Journal of Data Acquisition and Processing，1997，12（3）：171-174.（in Chinese）

［4］高鹰，谢胜利.一种变步长LMS自适应滤波算法及分析［J］.电子学报，2001，29（8）：1094-1097. GAOYing，XIE Sheng-li.A varialbe step size LMS adaptive filtering algorithm and its analysis［J］.Acta Electronica Sinica，2001，29（8）：1094-1097.（in Chinese）

［5］靳翼，邵怀宗.一种新的变步长LMS自适应滤波算法及其仿真［J］.信号处理，2010，26（9）：1385-1388. JIN Yi，SHAO Huai-zong.Anovel variable step siza LMS adaptive filtering algorithm and its simulation［J］.Signal Precessing，2010，26（9）：1385-1388.（in Chinese）

［6］宋彦，汪萌，戴礼荣，等.一种新的变步长自适应滤波算法及分析［J］.电路与系统学报，2010，15（4）：70-74. SONG Yan，WANGMeng，DAILi-rong，etal.A new variable step-size adaptive filtering algorithm and its analysis［J］.Journalof Circuits and Systems，2010，15（4）：70-74.（in Chinese）

［7］李善姬.一种用于自适应噪声抵消的变步长LMS算法［J］.电讯技术，2010，50（11）：30-33. LIShan-ji.A Variable-Step LMSAlgorithm for Adaptive Noise Canceller［J］.Telecommunication Engineering，2010，50（11）：30-33.（in Chinses）

［8］王军锋，宋国乡.小波变换的自适应均衡算法［J］.西安电子科技大学学报（自然科学版），2000，27（1）：21-38. WANG Jun-feng，SONGGuo-xiang.Wavelet transformed adaptive equalization algorithm［J］.Jounal of Xidian University（Natural Science Edition），2000，27（1）：21-38.（in Chinese）

［9］王丹，于枫.基于小波分析的自适应均衡技术的研究［D］.长春：吉林大学，2004：69-77. WANG Dan，YU Feng.The technology of adaptive equalization based on walevet analysis［D］.Changchun：Jinlin University，2004：69-77.（in Chinese）

WANG Dan was born in Dashiqiao，Liaoning Province，in 1979.She received the Ph.D.degree from Shanghai Jiaotong University in 2009.She is now an associate professor and also the instructor of graduate students.Her research concerns signal processing on communications and computer testing technology.

Email：wangdaniel2004＠163.com

杨雷（1979—），男，河南洛阳人，2006年于河南科技大学获硕士学位，现为讲师，主要研究方向为信号分析与处理、智能传感技术以及计算机检测技术；

YANG Lei was born in Luoyang，Henan Province，in 1979. He received the M.S.degree from Henan University of Science and Technology in 2006.He is now a lecturer.His research concerns signal analysis and processing，intelligent sensor technology and computer testing technology.

普杰信（1959—），男，河南鹿邑人，2007年于华中科技大学获博士学位，现为教授、博士生导师，主要研究方向为模式识别与图像处理。

PU Jie-xin was born in Luyi，Henan Province，in 1959.He received the Ph.D.degree from Huazhong University of Science and Technology in 2007.He isnow a professor and also the Ph.D.supervisor.His research concerns pattern recognition and image processing.

Adaptive Channel Equalization Using Variable Step Size LMS Algorithm Based on Wavelet Transform

WANGDan，YANG Lei，PU Jie-xin
（Electronic Information Engineering College，Henan University of Science and Technology，Luoyang 471003，China）

By combining the advantages of transform domain leastmean square（LMS）and variable step size LMSalgorithms，an adaptive linear equalization LMS algorithm using variable step size based on wavelet transform domain is proposed，where the step size is adjusted as an improved Sigmoid function.This function is simple and varies slowly as the error signal approaches zero.Moreover，the proposed method is compared with the traditional channel equalizationmethods in the trainingmode，the decision-directedmode and the hybridmode，respectively.Simulations show that the proposed methodmay offer higher convergence rate and better equalization performance than the conventional LMSmethod，the variable step size LMSmethod and the LMSmethod based on wavelet transform domain.

adaptive channel equalization；linear equalization；LMS algorithm；variable step size；wavelet transform

The National Natural Science Foundation of China（No.61101167）；The Science and Technology Foundation of Henan Province（No.112102210431）；The Scientific Research Foundation for the Doctors（No.09001409）；The Youth Science Foundation of Henan University of Science and Technology（2010QN0019）

TN911.5

A

10.3969／j.issn.1001-893x.2011.09.023

王丹（1979—），女，辽宁大石桥人，2009年于上海交通大学获博士学位，现为副教授、硕士生导师，主要研究方向为通信信号处理和计算机检测技术；

1001-893X（2011）09-0112-05

2011-07-11；

2011-08-08

国家自然科学基金资助项目（61101167）；河南省科技攻关计划项目（112102210431）；河南科技大学博士科研启动基金资助项目（09001409）；河南科技大学青年科学基金资助项目（2010QN0019）