一种精简结构的浮点蝶形运算单元设计✴

于龙洋，段文伟，李署坚

（北京航空航天大学电子信息工程学院，北京100191）

一种精简结构的浮点蝶形运算单元设计✴

于龙洋，段文伟，李署坚

（北京航空航天大学电子信息工程学院，北京100191）

论述了一种结构精简且高效的浮点数蝶形运算单元设计，单元内部模块的使用效率接近100%。采用串行全流水线结构设计，与并行结构相比节省了75%的硬件资源消耗。利用按时间抽取（DIT）的快速傅里叶变换（FFT）算法，通过VHDL编程实现了以该蝶形单元为基础的1 024点浮点FFT处理器。QUARTUS II中的仿真结果证明了设计的正确性。该设计已成功应用于一种音频信号分析仪的信号处理部分。

信号处理；蝶形运算单元；浮点数；快速傅里叶变换；流水线；按时间抽取

1 引言

硬件FFT实现相对于软件实现最大的特点就是速度优势，为了更充分地发掘FPGA在这方面的潜能，该方面的研究大都集中在如何进一步提高处理速度上，例如文献［1］通过采用基-16算法提高并行度，文献［2］通过优化设计使其最高工作频率达到200MHz。这些设计都注重提高并行度和工作频率以提高处理速度，但是对硬件资源的要求都很高。在很多对资源和成本要求严格的领域，硬件FFT处理器得不到应用，改善这种情况的根本措施在于尽量压缩其最小计算单位——蝶形运算单元的硬件开销。

本文设计在保证流水线正常工作前提下，最大限度地减少了蝶形单元内运算模块数量，并且蝶形单元内模块的利用率基本达到100%。最终在不影响运算精度和效率的情况下对一般的蝶形单元进行了结构上的压缩。为了验证这种设计的可靠性，采用按时间抽取的FFT算法设计实现了1 024点的浮点数FFT运算。在QUARTUS II中的仿真结果表明，采用这种方案设计的蝶形运算单元不会影响到浮点FFT处理器的精度和运算效率，并且极大地降低了FFT处理器的最小资源需求，使其具有更广泛的适用范围，具有很强的实用意义。

2 FFT算法

FFT算法基本上可以分为两大类，即按时间抽选（Decimation-in-time，DIT）法和按频率抽选（Decimation-in-frequency，DIF）法。两种算法具有相同的运算量和复杂度，且都可以作原位运算，只不过DIT是先作复乘后作加减，而DIF的复数乘法只出现在减法之后［3］。所以严格来说两种算法没有优劣之分，但由于DIT算法更加直观［2］，所以采用DIT算法。

根据选取的基数的不同，DIT又可分成基-2、基-4和分裂基算法。分裂基算法比较复杂，不易在高速电路中实现。其它两种算法相比来说，基-2算法具有程序简单、效率高、使用方便等特点，所以应用范围最广。基-4算法比基-2算法具有更高的运算效率，但由于复杂度高，实现起来不仅困难，而且硬件开销大。由于设计的原则就是压缩蝶形单元的硬件开销，所以最后选择基-2 DIT算法来设计蝶形运算单元。

3 基-2 DIT的蝶形运算

基-2 DIT蝶形运算结构如图1所示［3］。

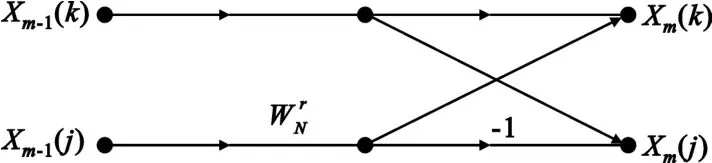
图1 基-2 DIT蝶形运算结构Fig.1 Structure of radix-2 DIT butterfly operation

由图1可知，每一次蝶形运算完成如下迭代运算：

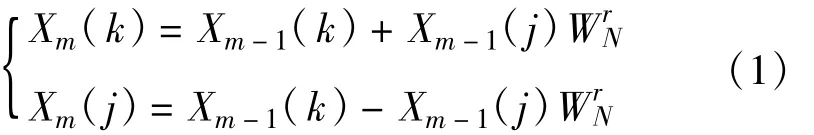
将上式中的变量写成实部和虚部构成的复数形式，即：

将这些复数形式代入上面的两个等式并令实部等于实部，虚部等于虚部，分别可得如下4个等式：

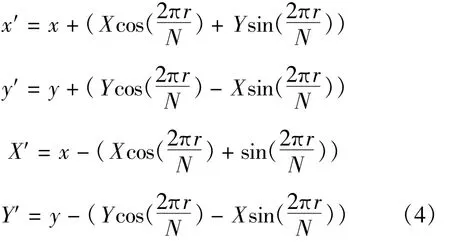
从上面的4个实数等式中可以看到，一个蝶形运算包含4个实数乘法和8个实数加法，但是这8个实数加法可以通过两级加法运算化简成6个加法，所以蝶形运算的流水线设计中包含两级加法器。

从功能上将整个蝶形运算单元看成一个封闭的系统，其输入包括参加蝶形运算的两个节点的实部和虚部4个数据，分别是x、y、X、Y，和系数WrN的实部和虚部两个数据（用cos和sin表示），总计6个数据；输出是这一级蝶形运算的结果，即对应节点在下一级上的实部和虚部4个数据，分别是x′、y′、X′、Y′，其功能如图2所示。

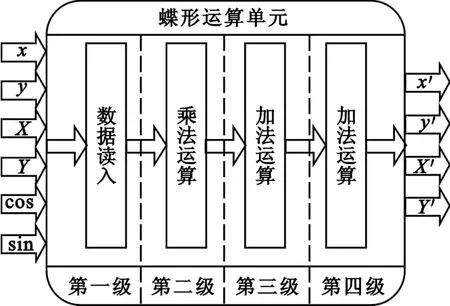
图2 蝶形运算单元功能示意图Fig.2 Functions of butterfly unit

4 蝶形运算单元的时序

参照图2，可以明确流水线包括4级，即数据读入级、乘法运算级、第一级加法运算和第二级加法运算。

遵循尽可能压缩蝶形单元硬件开销的原则，每一级流水线功能实现采用串行结构，这样乘法器和每一级加法器分别只用一个。流水线的每一级功能实现中运算次数的最大值是4，所以此时的蝶形运算周期是4个主时钟周期。流水线的时序如表1所示。表中的下标n表示蝶形运算序号，当n=1时，所有含有n-1下标项均为无效值。为了书写方便，表1中直接用cos和sin表示式（3）中的实部和虚部。一个蝶形运算周期包括4个阶段，依次记为C1～C4。

表1 蝶形运算单元的流水线时序Table 1 Pipeline sequence of butterfly unit

与文献［2］和文献［4］中选用的并行流水线结构对比，该设计方案具有以下优点：

（1）采用全流水线结构，充分体现出硬件处理的速度优势；合理地采用局部流水线技术，避免了并行结构引起的硬件资源消耗过多的弊端，因此更好地平衡了时间和硬件代价；

（2）将一次蝶形运算分解成4部分，所以以它为基础构建的FFT处理器可以把所有的数据放在同一个存储器中，只需要一个地址产生模块，所以可以降低后面FFT处理器的设计复杂度，减少硬件资源消耗；

（3）串行结构较并行结构会导致处理时间变长，但是这种劣势可以通过增加蝶形运算单元数目的方法来平衡，而采用全并行结构后，在资源比时间更为关键时却无能为力，所以本文设计具有更好的灵活性。

5 蝶形运算单元结构

蝶形运算单元的时序确定以后，就可以确定其具体结构了。其内部结构包括运算部分、寄存器部分、时序逻辑部分和多路选择器。运算部分包括一个浮点数乘法器、两个浮点数加法器和两个取反单元用以配合加法器实现减法运算；寄存器部分包括4个输入数据寄存器、两个乘法结果寄存器、两个一级加法结果寄存器、一个最终运算结果寄存器和一个移位寄存器；时序逻辑部分用来产生其它各个单元的工作时钟以保证整个流水线的正常工作。各个单元的工作时钟同主时钟关系的仿真结果如图3所示。

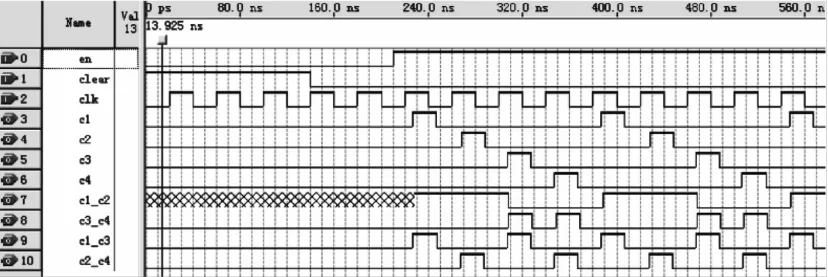
图3 时序逻辑单元输出仿真Fig.3 Output of sequence logic unit

蝶形运算单元内部具体结构如图4所示。由于浮点数加法运算的复杂性，一个时钟周期内根本无法完成运算，所以设计了一个多级流水线浮点加法器单元。为了保证整个流水线按照如表1所表示的时序正常工作，在第一级加法运算和第二级加法运算之间要加入必要的延时单元，延时功能通过移位寄存器实现。

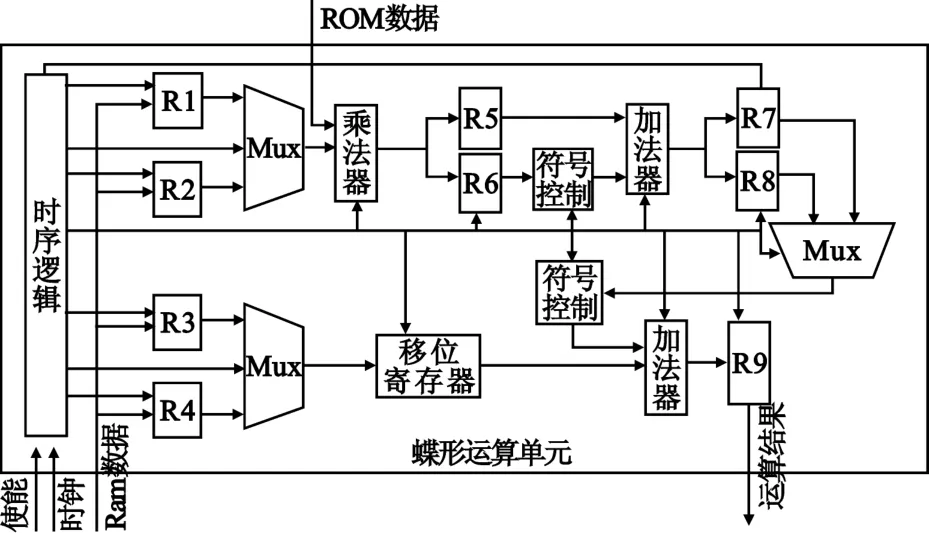
图4 蝶形运算单元结构框图Fig.4 Structure of butterfly unit

将图4与文献［2］中选用的并行流水线结构对比，可以发现采用串行全流水线结构后只用了并行结构1／4的硬件资源。并且可以将实数加法由8个简化为6个，提高了25%的加法运算效率。

综上所述，本文的设计方案可以极大地压缩碟形运算单元对硬件资源的消耗。

6 基-2 DIT的FFT结构

为了验证蝶形运算单元设计的可行性和可靠性，在它的基础上，通过增加地址产生单元、双口RAM以及旋转因子产生单元，设计实现了一个1 024点的基-2 DIT浮点FFT处理器，其结构组成如图5所示。

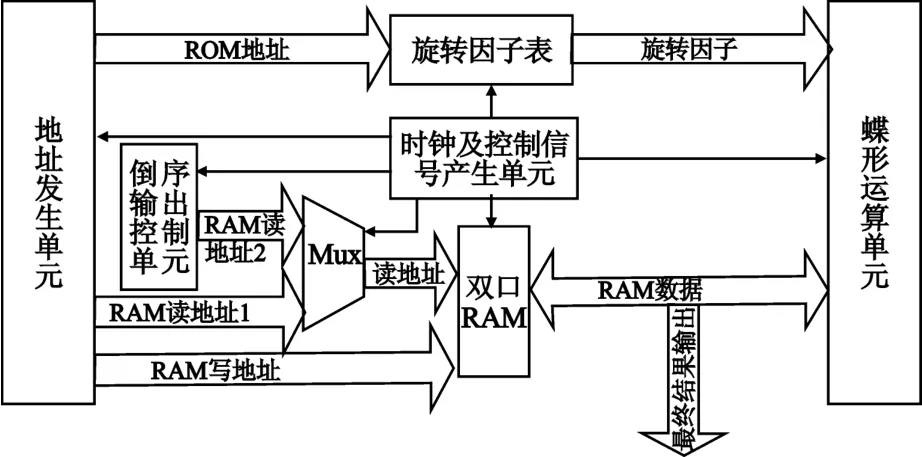
图5 基-2 DIT的FFT处理器结构框图Fig.5 Block diagram of radix-2 DIT FFT processor

旋转因子可以通过CORDIC算法迭代得到［5］，也可以采用查找表的方法实现。由于设计目标是减少资源开销，且面向的主要应用数据处理量不是很大，CORDIC算法的优越性得不到体现。相比较而言，查表法不仅设计简单，还具有线性度好的特点，所以FFT的设计采用查找表的方式获取旋转因子WrN。

采用输入自然序输出倒位序的算法［3］，由于该算法是原位运算，所以不需要中间存储器。地址发生单元负责产生对应级和对应序号的蝶形运算所需的数据和旋转因子所在的存储器地址。时钟及控制信号产生单元负责产生各个单元的工作时钟和控制信号。倒序输出控制单元负责产生倒序地址以输出正常顺序的运算结果。

7 设计的实现和仿真结果

7.1 蝶形运算单元和FFT处理器的实现

以Altera的Quartus II为设计工具，根据图4和图5所示的结构图，采取自底向上的设计方式，用VHDL编写各个模块，最后得到以设计的蝶形运算单元为基础的1 024点FFT处理器的逻辑综合结果如图6所示。

图6 1 024点FFT处理器逻辑综合结果Fig.6 Logic synthesis of1024-point FFT processor

7.2 仿真结果

为了验证蝶形运算单元和FFT处理器运算结果是否正确，用一个单位幅度、周期为16点的方波信号作为RAM的初始化数据，将FFT处理器的输出结果与Matlab对相同的方波信号处理的结果进行对比，以验证设计的功能是否实现。

FFT处理器的仿真结果如图7所示。选择5个不为零的数据与Matlab仿真结果进行对比，如表2所示，仿真结果与Matlab的计算结果一致，且精度很高。

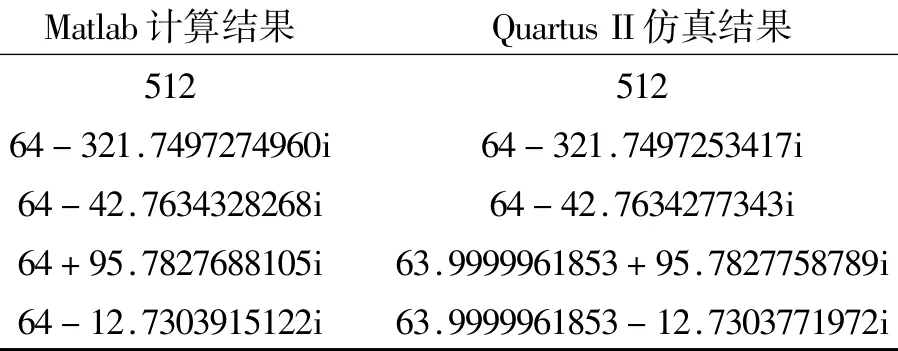
表2 计算结果精度比较Table 2 Comparison of precision

图7 T=25 ns时FFT处理器仿真结果Fig.7 Simulation result of FFT processor when T=25 ns

处理器的工作时钟周期用T表示，蝶形运算单元的处理周期为4T，1 024点FFT共包括10级蝶形，每级都有512个蝶形运算，加上流水线引起的延时为31T，所以总的处理用时为（31+52×10×4）T，即20 511T。以Altera公司的EP3C40F780C6为目标芯片在Quartus II 9.1中的仿真结果显示，整个FFT处理器的最高工作频率可达80 MHz，此时T取12.5 ns，可计算出整个运算用时为256.39μs。仿真结果如图8所示。

图8 主时钟频率为80 MHz时处理器仿真结果Fig.8 Simulation result of processor when the main clock frequency is80 MHz

8 结束语

将7.2节的仿真结果与文献［2］的仿真结果对比，可得到以下结论：

（1）由表2的对比结果可知，本文设计方案可以获得与文献［2］中相同的计算精度；

（2）同样地完成1 024点浮点FFT，采用本蝶形设计的FFT处理器需要的时钟周期数是文献［2］中处理器的20511／5520≈3.7倍，由本文第5节中的论述可知，该蝶形单元的硬件消耗只是其1／4。所以文中的串行全流水线结构设计不但可以大大压缩蝶形单元的结构，使得FFT处理器有更好的适用性，还可以提高硬件的利用效率。

该设计已成功应用于一种音频信号分析仪中，用来对采样的信号做傅里叶变换。该音频频谱仪信号处理速度快，硬件资源消耗低，在性能和资源方面达到了比较好的平衡。

［1］杨靓，黄士坦.一个高效的嵌入式浮点FFT处理器的实现［J］.信号处理，2003，19（2）：161-165. YANG Liang，HUANGShi-tan.Implementation ofa Highly Efficient Embedded Floating FFT Processor［J］.Signal Processing，2003，19（2）：161-165.（in Chinese）

［2］荣瑜，朱恩.一种高性能FFT蝶形运算单元的设计［J］.东南大学学报（自然科学版），2007，37（4）：565-568. RONGYu，ZHU En.Design of high-performance FFT butterfly unit［J］.Journal of Southeast University（Natural Science Edition），2007，37（4）：565-568.（in Chinese）

［3］程佩青.数字信号处理教程［M］.北京：清华大学出版社，2007. CHENG Pei-qing.Digital signal processing tutorial［M］. Beijing：Tsinghua University Press，2007.（in Chinese）

［4］Shaditalab.Self-sorting Radix-2 FFT on FPGAs Using Parallel Pipelined Distributed Arithmetic Blocks［C］／／Proceedings of 1998 IEEE Symposium on FPGAs.Montreal，Canada：IEEE，1998：337-338.

［5］杨军，郭跃东，丁俊.一种高速实时浮点蝶形运算单元的设计与实现［J］.仪器仪表学报，2010，31（3）：519-524. YANG Jun，GUOYue-dong，DING Jun.Design and implementation ofhigh-speed and real-time floating-pointbutterfly unit［J］.Chinese Journal of Scientific Instrument，2010，21（3）：519-524.（in Chinese）

YU Long-yang was born in Shandong Province，in 1989.He received the B.S.degree from Shandong University in 2010.He is now a graduate student.His research interests include spread spectrum communication and satalite navigation.

Email：sdyly0127＠163.com

段文伟（1987—），女，山东人，2010年于南京农业大学获学士学位，现为北京航空航天大学硕士研究生，主要研究方向为扩频通信；

DUANWen-wei was born in Shandong Province，in 1987. She received the B.S.degree from Nanjing Agricultural University in 2010.She is now a graduate student.Her research direction is spread spectrum communication.

李署坚（1953—），男，湖南人，副教授、硕士生导师，主要研究方向为扩频通信、高动态GPS信号接收技术、RFID关键技术等。

LIShu-jian was born in Hunan Province，in 1953.He is now an associate professor and also the instructor of graduate students. His research interests include spread spectrum communication，receiving technology of HDR GPS signal，RFID key technology.

Design of a Floating-point Butterfly Unit w ith Sim plified Structure

YU Long-yang，DUANWen-wei，LIShu-jian
（School of Electronic and Information Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China）

This paper presents an efficient design of butterfly unitwith simplified structure.The occupating coefficient of innermodules of the unit is almost100%.This unit uses a full pipeline structure，which saves 75% of the hardware resource consumption compared with the parallel structure.A floating-point FFT processor based on this butterfly unit is realized by using the FFT algorithm of DIT（Decimation-in-time）.The simulation results of QUARTUS IIdemonstrate the correctness of the design.This design has been successfully applied in the signal processing part of an audio signal analyser.

signal processing；butterfly unit；floating-point；FFT；pipeline；DIT

TN911.72

A

10.3969／j.issn.1001-893x.2011.09.015

于龙洋（1989—），男，山东人，2010年于山东大学获学士学位，现为硕士研究生，主要研究方向为扩频通信和卫星导航；

1001-893X（2011）09-0073-05

2011-03-30；

2011-05-31