美国货币政策对中国货币政策的溢出效应研究*
邢天才,唐国华
(1.东北财经大学 金融分析与模拟实验室,辽宁 大连 116025;2.东北财经大学 研究生院,辽宁 大连 116025)
长期以来,美国在全球经济中扮演着超级大国的角色,在国际经济政策的制定中也占据十分重要的地位,Kim曾指出“经济最发达国家的货币政策对其他国家的影响最为显著,而美国以外的其他国家的货币政策的国际传递效应则较之相比微弱的多”[1]。因此,当代学者十分关注美国货币政策的变化,尤其是在2007年美国爆发次贷危机之后,学者们更加关注美国货币政策的调整对全球经济的影响。中国自改革开放以来,经济发展取得了重大成就,对外开放度不断提高。随着对外开放的深入,中国经济与世界经济之间的联系也达到了空前紧密的程度,来自外部的货币政策冲击尤其是来自美国的货币政策冲击对中国货币政策的影响也越来越大。本文就美国货币政策对中国货币政策的溢出效应进行研究。Cooper提出货币政策的溢出效应和溢入效应,其中溢出效应指一国货币政策不仅会影响到本国经济的运行,还会通过各种途径影响到其它国家,相应的他国的货币政策影响到本国的经济就是货币政策的溢入效应[2]。美国货币政策对中国货币政策的溢出效应包含两层含义:第一层含义是美国货币政策对中国货币政策的影响,即美国的联邦基金利率调整是否会促使中国的利率或者是货币供应量发生变化;第二层含义是中国货币政策的自主性,即中国的狭义货币政策是否受到本国汇率变化的影响。
一、文献综述
Sheehan研究发现美国的货币政策对不同国家的影响不同。澳大利亚和德国的货币供应量受到美国货币供应Ml的影响,而意大利、日本、加拿大和英国的货币供应量并没有显著地受到来自美国货币供应量的影响[3]。Stam等考察了美国的货币供应量冲击对日本和欧盟的影响,文章认为美国的货币供应量对比利时、英国的影响较大,而对日本、德国和意大利的影响较小[4]。Sheehan采用了标准的IS-LM模型检验了美国货币政策冲击对外国货币供应量增长的影响,他认为,如果不考虑美国的经济变量,那么外国的货币政策决策过程是不完整的[5]。Chung则研究了美国、日本和德国货币政策之间的相互依赖,研究发现在浮动汇率制度下,一国的货币当局对其他国家的货币政策反应强烈[6]。Grilli和Roubini发现其他G-7国家的货币政策与美国货币政策之间的相互依赖性很强[7]。而Kim则得出不同的结论,他认为除加拿大以外,其他G-7国家的中央银行对美国货币政策的反应都不显著[1]。
二、研究方法及数据来源
本文采用SVAR方法分析美国货币政策对中国货币政策的溢出效应。USGDP代表美国的产出序列,采用取对数的美国月度工业生产指数来衡量;USCPI代表美国的通胀序列,用美国的月度CPI计算美国的月度通货膨胀水平来衡量;USNX代表美国的国际收支状况,用美国净出口数据绝对值的对数序列来衡量;FFR代表联邦基金利率;USM2代表美国的广义货币供应量序列,对基础数据进行了去对数的处理;CHI代表中国的利率水平,用中国的1年期贷款利率来衡量;用CHM2代表中国的广义货币供应量序列,并对基础数据进行了取对数的处理。具体的模型分析框架如下:

其中,p为选择的滞后阶数,最后一个变量Yt代表模型中考察的美国货币政策溢出冲击的变量。结构向量自回归模型中变量之间的当期关系并没有直接给出,而是隐藏在误差项相关关系的结构中。SVAR模型正是运用了施加约束条件的方法解决了参数过多的问题。一般来说,当系数矩阵C0为下三角矩阵时,结构向量自回归模型具有递归结构,此时,变量间的同期影响具有Wold因果链①任意两个变量的同期影响方式都是单向的,位置靠前的变量对位置靠后的变量具有当期影响力,而位置靠后的变量对位置靠前的变量没有当期影响力。的形式。本文的SVAR模型正是采用了这种约束条件。为了方便,下文中将 (1)的实证模型表示为本文的样本区间如无特殊说明为1995年1月到2010年12月,采用月度数据进行分析,总计192个数据样本。原始数据主要来源于Wind资讯数据库、Resset数据库、国际货币基金组织数据库和美联储网站。
三、实证检验及结果分析
1.美国货币政策对中国利率的溢出效应
美国货币政策的代理变量为联邦基金利率,但中国的同业拆借利率却并不能很好地反应出中国的货币政策走势。原因在于,中国的利率市场化改革还没有完成,中央银行对利率进行调整的实际操作是先确定1年期存贷款利率,再推出各档期限的利率。因此,本文采用1年期贷款利率作为中国货币政策的代理变量。
利用SVAR模型进行分析,估计模型为 (1),从表1中的信息准则数据中可以看到,对这个向量系统,滞后阶数为1和滞后阶数为3没有区别。本文在进行结构向量自回归时分别估计了滞后1阶和滞后3阶的模型,从脉冲响应和方差分解的结果来看,并没有太大的区别,因此文中只列出了滞后3阶的结果。

表1 政策渠道检验模型的滞后阶数选择标准 (1)
确定滞后阶数后,用递归假设进行估计,美国货币政策代理变量FFR对中国1年期贷款利率的脉冲响应函数如图1所示。从图1可以看到,FFR一个标准差的新息冲击,对中国的利率有正向的影响,4个月的脉冲值达到顶峰,为0.1295,脉冲值在10个月后基本稳定为0.11左右。以上结果反映出了美国货币政策对中国货币政策的溢出效应,美国加息,中国也会随之加息。
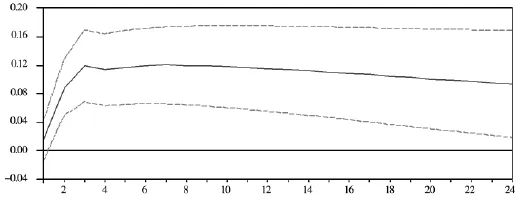
图1 美国货币政策冲击对中国利率的脉冲响应图
从表2的方差分解结果可以看出,中国1年期贷款利率变动的预测方差中,美国货币政策冲击的贡献率在1个月后不足1%,两个月后就达到10.66%,之后贡献率不断增大,在7个月后达到峰值25.37%。这一结果反映出中国的利率政策与美国利率政策的一致性,当美国利率提高时中国的利率也会提高。从利率变动的动态关系中我们可以看到,开放经济中货币政策的溢出效应是十分明显的,美国通过改变联邦基金利率对其国内经济进行调整时,也引起了中国利率政策的调整。当然,这种利率的同向调整离不开大量的资本流动,虽然我们的资本项目还没有完全放开,但是资本流动规模还是很可观的。目前中国的利率市场化还没有完全结束,中央银行还没有放开对1年期存贷款利率的限制,这意味着中国1年期贷款利率的调整反映的还是中央银行的政策意图,从货币政策国际协调的角度出发,中美利率的联动实际上很多是中国的中央银行的一种被动协调。

表2 FFR冲击对CHI变动的贡献率 (方差分解)
2.美国货币政策对中国货币供应量的溢出效应
多年来,中国一直采用货币供应量作为货币政策的中介目标,因此检验货币政策的国际溢出效应时,分析FFR对货币供应量的动态影响十分重要。由于缺乏1995年1月到1995年11月的广义货币供应量的统计数据,本文采用的检验区间为1995年12月到2010年12月。采用与上文一致的检验方法,考察包含模型。从表3可知,该向量自回归系统选择的滞后阶数为3。
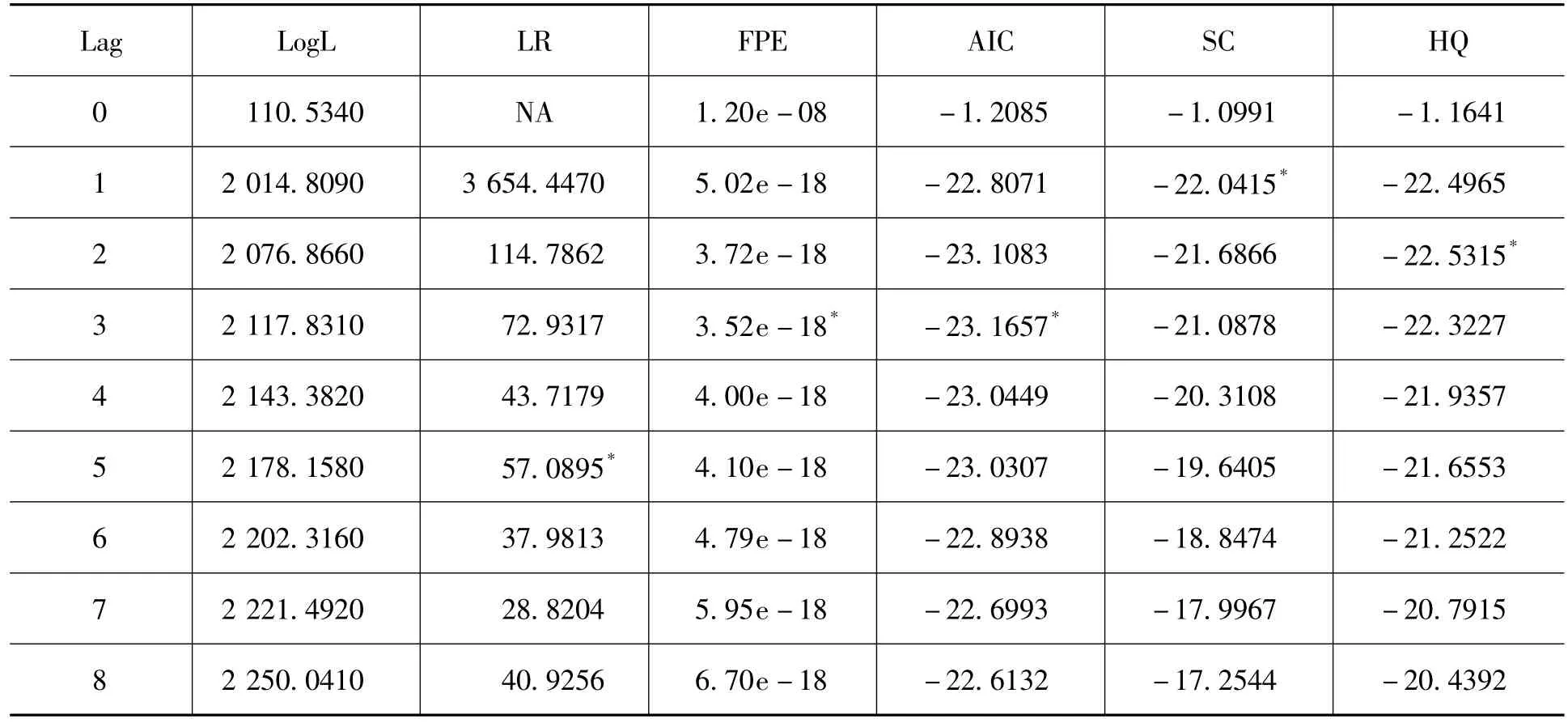
表3 政策渠道检验模型的滞后阶数选择标准 (2)
在进行滞后阶数的选择后,利用递归假设进行估计,得到了FFR对中国广义货币供应量的脉冲响应函数,如图2所示。从脉冲响应函数可以看到,美国联邦基金利率一个标准差的新息冲击对中国货币供给量的影响是正的。1个月的脉冲值为0.0007,之后随着时间的推移逐步上升,在7个月达到脉冲值的顶峰0.0016。这个结果意味着,美国的货币政策对中国的货币供应量有影响,当美国实施紧缩的货币政策时,中国的货币供应量反而是上升的。利率政策同向变动,而货币供应量却反向变动,这一结果的对比表面看起来是矛盾的,实际上却反应出在当前的经济环境下,中国虽然实行的是以货币供应量为中介目标的货币政策操作策略,但对货币供应量的控制力并不强。
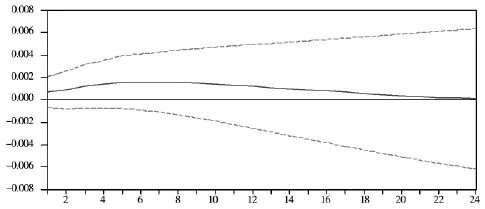
图2 美国货币政策冲击对中国广义货币供应量M2的脉冲响应图
从表4方差分解的结果可以看出,在中国广义货币供应量 M2变动的预测中,美国货币政策代理变量联邦基金利率冲击的贡献率从第一个月的不足1%,逐渐上升,八个月后的贡献率达到2.69%。

表4 FFR冲击对CHM2变动的贡献率 (方差分解)
3.中国货币政策的自主性检验
伴随着全球金融一体化进程对资本流动的关注,理论界也提出了一些方法对货币政策自主性进行检验。检验货币政策自主性的基本思想是,如果中央银行在公开市场上进行操作从而来改变其国内的资产规模进而影响到货币供应量,国内的资产价格就会发生变化,相应的收益率也会发生变化。如果在资本自由流动的背景下,国际流动资本的套利活动就会抵消央行国外净资产发生相反方向的变化,从而国内的货币量就不会发生变化。简单来说,如果资本流动性较低,那么中央银行拥有的货币政策自主性就会比较高。
对货币政策自主性的检验主要是考察中央银行的资产负债表结构的变化。从中央银行的资产负债表出发,一国的货币供应可以来源于国内的部分和国外的部分,其中前者表现为央行的国内净资产,后者表现为央行的国外净资产。用TA表示央行的总资产,DA表示央行的国内净资产,FA表示央行的国外净资产,则存在如下的数量关系:

以中国的央行为例,国内净资产DA主要由对政府债券、其它金融机构债券、非金融性公司债券以及其他资产组成;国外净资产FA主要由外汇、黄金和其它国外资产组成。
如果一个国家的货币政策有较大的独立性,那么中央银行可以通过改变DA来改变TA,从而达到影响货币供应量的目的。但是,如果一个国家的中行在改变DA的同时,引起了FA相应的反方向变化,TA就可能不会发生改变或者变化非常小。换言之,在开放经济中,如果DA的变化会导致FA的变化,且dDA和dFA之间是反向相关关系,那么这个国家的货币政策自主性就受到了很大的限制。从2002年1月到2010年7月中国人民银行国内净资产和国外净资产的变动情况可以看出,央行的国内净资产和国外净资产在我们的考察区间内都呈现出了上升的趋势,并且国外净资产的上升趋势要更加明显。由于中国经济处于高速的发展阶段,经济规模不断扩大,因此央行两类资产的规模都表现出上升趋势是合理的。在这样的情况下,央行实施货币政策的方向更多地应该从两类资产规模变动率的波动上。也就是说,当央行实施宽松的货币政策时,总资产规模的增长率上升;当央行实施紧缩的货币政策时,总资产规模的增长率下降。
利用SPSS16.0计算出央行国内净资产变动的波动率和国外净资产变动的波动率之间存在着负的相关关系,系数为-0.5890,该相关系数在1%的显著性水平下显著。姜波克等曾经计算过1987—1997年二者季度数据之间的相关系数,结论为-0.37[8]。比较这两个数据可以看出,随着中国经济开放度的提高,央行的国内净资产变动的波动率和国外净资产变动的波动率之间负的相关性在大幅的提高,中国央行的货币政策自主性在不断地降低,从这个角度来看,必须充分重视中国货币政策的国际协调,否则央行的货币政策将是无效的,央行利用国内的资产进行的货币政策将很大一部分被国外净资产的被动调整所抵消。进一步分析,我们利用央行国内净资产变动的波动率和国外净资产变动的波动率进行格兰杰因果关系检验。综合考虑AIC等信息准则 (如表5所示),本文选取的滞后阶数为4。

表5 格兰杰因果检验滞后阶数选择标准
确定了滞后阶数后,我们首先检验央行的国内净资产变动率的波动是否是央行国外净资产变动率波动的格兰杰原因。建立如下的检验模型:
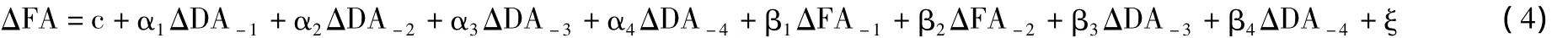
检验是否为格兰杰原因的零假设为H0:α1=α2=α3=α4=0。利用Eviews6.0进行检验,得到F统计量为2.1643,伴随概率为0.0796。这一结果表明,在5%的显著性水平下,拒绝原假设,此时央行国内净资产变动的波动是央行国外净资产变动波动的格兰杰原因。表明央行国外净资产变动的波动对国内净资产变动的波动有显著的影响,央行实施冲销性的货币政策,来自外部的冲击被央行国内净资产变动的波动所抵消。
同样的方法,检验央行的国外净资产变动率的波动是否是央行国内净资产变动率的波动的格兰杰原因。建立如下的检验模型:

检验是否为格兰杰原因的零假设为H0:β1=β2=β3=β4=0。同样利用Eviews6.0进行检验,得到F统计量为1.0360,伴随概率为0.3933。结果表明,在5%的显著性水平下,拒绝原假设,此时央行国外净资产变动的波动是央行国内净资产变动波动的格兰杰原因。这样的结果表明,央行通过采取改变国内资产规模从而改变货币政策方向的愿望难以实现。
四、结 论
本文利用SVAR等方法对美国货币政策对中国货币政策溢出效应的实证研究表明,中国的货币政策会受到美国货币政策调整的影响。结果显示,美国的利率政策变动会引起中国的利率发生同方向的变动,来自美国的货币政策冲击在两个月后可以解释中国利率变动的10%。美国的货币政策冲击会引起中国广义货币量的同向变化,其影响大小和解释力度在第七个月左右达到最大。对货币政策自主性检验的结果显示,在当前的经济背景下,中国的央行在制定货币政策时受到国际因素的影响很大,央行的货币政策虽然采取了冲销性的操作策略,可是并不能够有效地应对外部冲击。
美国的货币政策之所以能够对中国的货币政策产生这样的溢出效应,原因在于,美国货币政策的调整必然会导致美元汇率的波动以及国内外利差的波动,在中国资本管制逐渐放松、汇率制度还没有完全浮动的背景下,要防止国际短期资本的流动对中国国内金融市场的冲击,维持人民币的汇率稳定,势必会影响到中国货币政策的独立性,中国货币政策的制定过程也必然会渗透了美国的因素。
[1]Kim,S.International Transmission of U.S.Monetary Policy Shocks:Evidence from VAR's[J].Journal of Monetary Economics,2001,48(2):339-372.
[2]Cooper,R.N.Macroeconomic Policy Adjustment in Interdependent Ecnomics[J].The Quarterly Journal of Economics,1969,83(1):1 -24.
[3]Sheehan,R.G.Does U.S.Money Growth Determine Money Growth in Other Nations?[J].Federal Bank of St.Louis Journal Review,1987,69(1):5 -14.
[4]Stam,A.,Delorme,Jr.C.,Fintenstadt,B.Cross National Money - Income Causality for the Floating Exchange Rate Period:Has the Influence of U.S.and German Money Persisted?[J].Journal of Macroeconomics,1991,13(2):207-237.
[5]Sheehan,R.Influences on Foreign Monetary Policy[J].Journal of Money,Credit& Banking,1992,24(4):447 -464.
[6]Chung,J.W.Monetary Interdependence among G -3 Countries[J].Applied Economics,1993,25(5):681 -688.
[7]Grilli,V.,Roubini,N.Liquidity and Exchange Rates:Puzzling Evidence from the G -7 Countries[R].Yale University Working paper,1995.
[8]姜波克,傅浩,钱钢.开放经济下的政策搭配[M].上海:复旦大学出版社,1999.112-120.

