偏心与安装误差对封闭差动人字齿轮传动系统静力学均载特性的影响*

朱增宝 朱如鹏 鲍和云 靳广虎

(南京航空航天大学机电学院，江苏南京210016)

封闭差动人字齿轮传动系统是星型轮系封闭差动行星轮系的组合传动机构.广泛应用于工程机械、船舶运输、航空航天的动力传动等诸多领域.利用多个行星轮和星轮分担载荷，形成功率分流，具有体积小、质量轻、传动平稳、承载能力强、传动效率高等优点.不可避免的制造和安装误差以及构件的变形等因素是造成行星轮和星轮载荷不均的主要因素，载荷的均衡分配是发挥封闭差动人字齿轮传动系统特点和保证正常工作的重要条件.

国外学者对行星传动系统均载特性作了许多研究，文献［1-2］中对行星传动系统静力学均载特性进行了较为全面的研究，文献［3-6］对行星传动系统均载特性进行了动力学理论研究，文献［7-8］对行星传动系统均载特性进行了实验研究;国内肖铁英等［9］研究了行星传动系统静力学载荷不均匀系数计算方法，方宗德等［10］研究了行星传动系统的动态均载特性，孙智民等［11］研究了封闭差动行星传动系统动力学特性.这些研究主要针对直齿轮的传动系统，模型中没有包含中间浮动构件.目前，针对封闭差动行星传动系统静力学均载特性的研究还鲜见报道.文中考虑了中间浮动构件的影响，建立了封闭差动人字齿轮传动系统静力学模型，分析了偏心与安装误差对传动系统静力学均载特性的影响，研究成果可以为封闭差动人字齿轮传动系统的误差精度等级控制及齿轮安装提供理论依据.

1 系统的静力学模型

图1为封闭差动人字齿轮传动系统示意图.系统由差动行星轮系和星型轮系进行封闭式联接组成.下文分别称这两个轮系为差动级和封闭级.差动级包含太阳轮 Zs1、行星轮 Zpi(i=1，2，…，N)、内齿轮Zr1、行星架H、中间浮动构件Zg1、浮动齿圈Zf1等构件;封闭级包含太阳轮 Zs2、星轮 Zmj(j=1，2，…，M)、内齿轮Zr2、中间浮动构件Zg2、浮动齿圈Zf2和输出轴L等构件.输入功率W1经过差动级太阳轮Zs1分流到行星架H和内齿轮Zr1后，再由行星架H和浮动齿圈Zf2汇流到输出轴L上，以功率W2输出.图1中的中间浮动构件Zg1和Zg2也称双齿联轴器，是封闭差动人字齿轮传动系统中不可缺少的构件，有均载作用.文中N为行星轮个数，M为星轮个数.

图2(a)为差动级静力学模型，采用以行星架转速ωH旋转的动坐标系;图2(b)为封闭级静力学模型，采用固定坐标系.

图1 封闭差动人字齿轮传动系统示意图Fig.1 Sketch map of encased differential herringbone train

图2 封闭差动人字齿轮传动系统静力学模型Fig.2 Static model of encased differential herringbone train

图2 中，Ks1、Kp、Kr1、Ks2、Km和 Kr2分别为齿轮Zs1、Zpi、Zr1、Zs2、Zmj和 Zr2的支撑刚度;KH为行星架H在行星轮公转半径rH上的等效切向刚度;KHL、Kf1s2和 Kf2L分别为联接 H 与 L、Zf1与 Zs2、Zf2与 L 的扭转刚度;Kg1q、Kf1q、Kg2q和 Kf2q分别为 Zr1与 Zg1、Zg1与Zf1、Zr2与 Zg2和 Zg2与 Zf2接触的切向刚度;Gs1、Gp、Gr1、Gs2、Gm和 Gr2分别为齿轮 Zs1、Zpi、Zr1、Zs2、Zmj和Zr2的重量;Fpi为各行星轮的公转离心力.

封闭差动人字齿轮传动系统共有(18+3×(N+M))个自由度，其广义位移列向量X表示为

式中:xs1、xpi、xr1、xs2、xmj和 xr2分别为齿轮 Zs1、Zpi、Zr1、Zs2、Zmj和 Zr2沿基圆半径扭转的线位移;xg1、xf1、xg2和 xf2分别为构件 Zg1、Zf1、Zg2和 Zf2沿分度圆半径扭转的线位移;xH为行星架H在其半径rH扭转的线位移;xL为输出轴L与浮动齿圈Zf2接触处rL上的线位移;Hs1与 Vs1、Hpi与 Vpi和 Hr1与 Vr1分别为齿轮Zs1、Zpi和Zr1中心在旋转坐标系中的横向与纵向位移;Hs2与 Vs2、Hmj与 Vmj和 Hr2与 Vr2分别为齿轮 Zs2、Zmj和Zr2中心在固定坐标系中的水平方向与垂直方向位移.

2 系统的静力学方程

差动级齿轮副Zpi与Zr1之间称为内啮合，Zs1与Zpi之间称为外啮合，一起简称为差动级内外啮合;封闭级齿轮副Zmj与Zr2之间称为内啮合，Zs2与Zmj之间称为外啮合，一起简称为封闭级内外啮合.

令Prpi和Pspi分别为差动级内外啮合的弹性啮合力，则

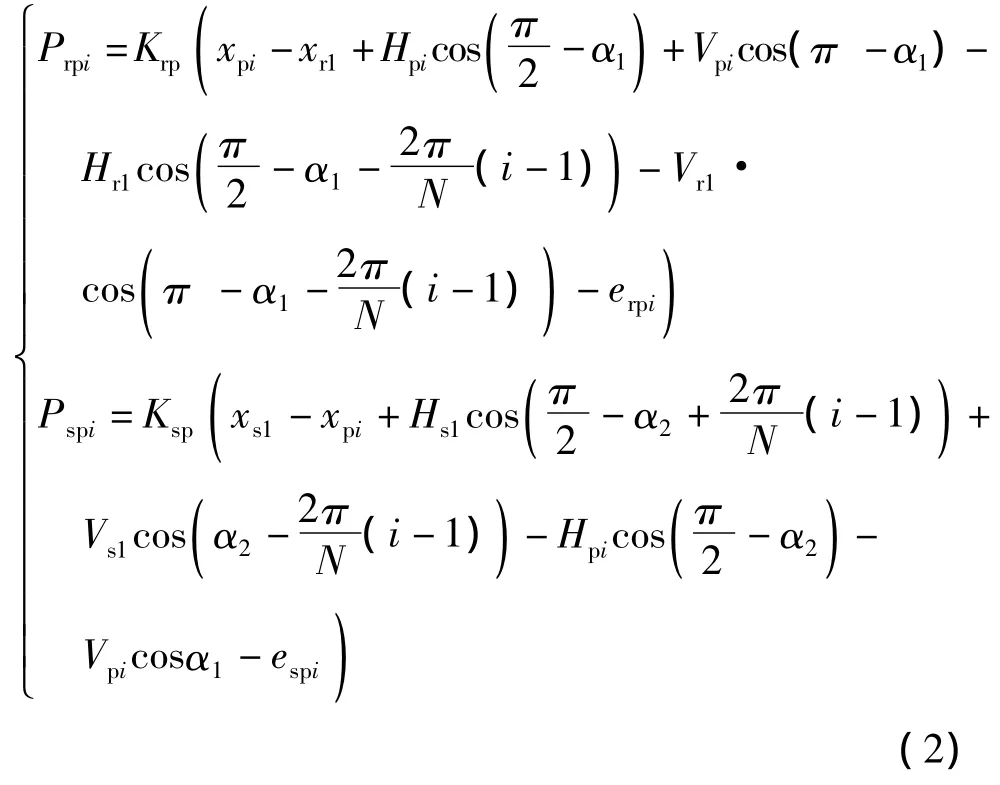
式中:Krp和Ksp分别为差动级内外啮合平均啮合刚度;α1和α2分别为差动级内外啮合的啮合角;erpi和espi分别为差动级内外啮合线上误差等效位移;2π·(i-1)/N表示第i个行星轮相对第1个行星轮的位置角.

令Prmj和Psmj分别为封闭级内外啮合的弹性啮合力，则

式中:Krm和Ksm分别为封闭级内外啮合平均啮合刚度;α3和α4分别为封闭级内外啮合的啮合角;ermj和esmj分别为封闭级内外啮合线上误差等效位移;2π·(j-1)/M表示第j个星轮相对第1个星轮的位置角.

人字齿平均啮合刚度采用国标GB/T3480—1997斜齿轮啮合刚度计算公式按刚度并联方式计算.太阳轮与各个行星轮/星轮之间及各个行星轮/星轮内外啮合之间的相位差按Parker等［12］推导的公式计算.

考虑中间浮动构件的影响，建立的封闭差动人字齿轮传动系统静力学方程见式(4)-(15).

式中:mp为行星轮质量;t为时间历程;PD为输入转矩TD在太阳轮Zs1基圆半径rs1b上的等效力，PD=TD/rs1b;PL为负载转矩TL在输出轴L与浮动齿圈Zf2接触处rL上的等效力，PL=TL/rL;rs2b为太阳轮Zs2的基圆半径;rf1b和rf2b分别为浮动齿圈Zf1和Zf2的分度圆半径.

3 误差等效位移

进行静力学均载研究时，影响行星轮和星轮间载荷分配的误差主要有偏心误差和安装误差.由于采取中心轮(太阳轮和内齿轮)浮动均载方式，行星架作为参照，其偏心及安装误差包含在各齿轮误差中，所以认为行星架偏心及安装误差为零.算例中行星轮和星轮支撑轴的制造与安装精度足够精确，为简化分析，不考虑行星轮和星轮的安装误差.

各齿轮误差对齿轮副啮合的影响体现在啮合线方向上的位移变化，研究时把以上两种误差转化到齿轮副啮合线上.误差转化到齿轮副啮合线上的处理方法有多种，如用实测的误差值、实测的齿轮误差曲线、傅里叶级数、简谐函数和随机数等表示［13］.简谐函数具有直观、简洁的特点，行星传动系统均载研究常采用简谐函数进行行星传动系统误差分析.文中用简谐函数把误差转化到齿轮副啮合线上，叠加后得到差动级齿轮偏心与安装误差在齿轮副啮合线上等效位移为

式中:Es1、Epi和 Er1分别为齿轮 Zs1、Zpi和 Zr1的偏心误差;φs1、φpi和 φr1分别为齿轮 Zs1、Zpi和 Zr1的偏心误差初相角;As1和Ar1分别为齿轮Zs1和Zr1的安装误差;δ1和 δ2分别为齿轮 Zs1和 Zr1的安装误差位置角;ω1为差动级的啮合齿频;ωH为行星架H的角速度;ωsH、ωpH和 ωrH分别为齿轮 Zs1、Zpi和 Zr1相对行星架H的相对角速度.

得到的封闭级齿轮偏心与安装误差在齿轮副啮合线上等效位移为

式中:Es2、Emj和 Er2分别为齿轮 Zs2、Zmj和 Zr2的偏心误差;φs2、φmj和 φr2分别为齿轮 Zs2、Zmj和 Zr2的偏心误差初相角;As2和Ar2分别为齿轮Zs2和Zr2的安装误差;δ3和 δ4分别为齿轮 Zs2和 Zr2的安装误差位置角;ω2为封闭级的啮合齿频;ωs2、ωm和 ωr2分别为齿轮 Zs2、Zmj和 Zr2的角速度.

4 载荷不均匀系数计算

行星轮/星轮之间载荷分配均匀性用载荷不均匀系数表示，载荷不均匀系数越大载荷分配越不均衡.采用外啮合载荷不均匀系数反映行星轮/星轮载荷分配的均匀性.

静力学载荷不均匀系数Ω为

式中:Nc为行星轮或星轮个数;F为齿轮副的啮合力;P为理论载荷.

求解静力学方程式(4)-(15)获得(18+3(N+M))个待求变量，即广义位移列向量X.将X代入式(2)和式(3)中，得弹性啮合力 Frpi、Fspi、Frmj和 Fsmj.则差动级第i个行星轮的载荷不均匀系数Ωspi和封闭级第j个星轮的载荷不均匀系数Ωsmj为

式中:T2为作用在封闭级太阳轮Zs2基圆半径rs2b上的转矩.

则差动级和封闭级静力学载荷不均匀系数Ωp和Ωm为

5 均载特性分析

文中针对某封闭差动人字齿轮减速器进行分析.减速器的基本参数如下:差动级模数m1=7mm，行星轮个数N=3，太阳轮齿数Zs1=37，行星轮齿数Zp=56，内齿轮齿数Zr1=149，齿宽系数φd1=1.2，压力角αn1=20°，螺旋角 β1=22°;封闭级模数 m2=7mm，星轮个数M=5，太阳轮齿数Zs2=71，星轮齿数Zm=39，内齿轮齿数Zr2=149，齿宽系数φd2=0.6，压力角 αn2=20°，螺旋角 β2=22°;输入轴转速n=3000r/min，输入功率P=2000 kW;差动级和封闭级的中心轮(太阳轮和内齿轮)的支撑刚度为3×108N/m，行星轮和星轮支撑刚度为109N/m;各齿轮偏心误差为32μm，中心轮安装误差为32μm.

为研究偏心误差对系统载荷不均匀系数的影响，安装误差不变，改变差动级和封闭级各个齿轮偏心误差，获得系统载荷不均匀系数曲线如图3和图4所示.图中E为偏心误差.图3(a)为系统两级载荷不均匀系数分别与各级太阳轮偏心误差变化关系，图3(b)为系统两级载荷不均匀系数分别与各级内齿轮偏心误差的关系，图4(a)为系统两级载荷不均匀系数分别与行星轮和星轮偏心误差的关系.图3和图4(a)中，随着两级太阳轮、内齿轮和行星轮/星轮偏心误差增大，系统两级载荷不均匀系数增大.

图3 系统两级载荷不均匀系数与中心轮偏心误差变化关系Fig.3 Relationship between load sharing factors of two stages and eccentric errors of center gears

图4 系统两级载荷不均匀系数与行星轮/星轮偏心误差变化关系Fig.4 Relationship between load sharing factors of two stages and eccentric errors of planet/star gears

图4(a)中，差动级各行星轮和封闭级各星轮偏心误差的初相角不相同，当差动级各行星轮和封闭级各星轮偏心误差的初相角取相同值时，系统两级载荷不均匀系数分别与差动级行星轮和封闭级星轮偏心误差的关系如图4(b)所示.由图4(b)可见，差动级载荷不均匀系数为1.0698，封闭级载荷不均匀系数为1.0452，差动级和封闭级载荷不均匀系数均不随行星轮和星轮偏心误差变化而改变.行星轮/星轮偏心误差初相角相同时各行星轮和星轮偏心误差沿啮合线的等效位移互相抵消，所以偏心误差的大小对系统两级载荷不均匀系数没有影响.对于一般的大批量生产的行星传动系统，采取行星轮/星轮偏心误差初相角相同的措施会增加安装工序，提高生产成本，不太现实;对于载荷分配均匀性要求高的重要传动系统，装配时可以通过对行星轮/星轮的偏心相位进行选配和调整，使行星轮/星轮偏心误差初相角相同来实现均载.

为研究安装误差对系统载荷不均匀系数的影响，偏心误差不变，改变差动级和封闭级的太阳轮和内齿轮的安装误差，获得系统载荷不均匀系数曲线如图5所示，图5中A为安装误差.图5(a)为系统两级载荷不均匀系数分别与各级太阳轮安装误差的关系，图5(b)为系统两级载荷不均匀系数分别与各级内齿轮安装误差的关系.图5中，随着两级太阳轮和内齿轮安装误差的增大，系统两级载荷不均匀系数增大.图3-5说明误差越大，载荷不均匀系数越大，载荷分配越不均衡.这一规律与行星传动均载研究的已有结论一致，说明该系统的静力学建模是可行的.

图5 系统两级载荷不均匀系数与中心轮安装误差变化关系Fig.5 Relationship between load sharing factors of two stages and installation errors of center gears

上文研究了系统两级载荷不均匀系数分别随偏心误差和安装误差变化的规律.传动系统受偏心与安装误差的共同作用，为研究偏心与安装误差共同作用对系统两级载荷不均匀系数的影响，首先计算偏心与安装误差单独作用下系统两级的载荷不均匀系数.

不考虑安装误差影响，假设安装误差为0，偏心误差单独作用下系统两级各行星轮和星轮载荷不均匀系数曲线如图6所示，差动级载荷不均匀系数为1.0522，封闭级载荷不均匀系数为1.0252.不考虑偏心误差影响，假设偏心误差为0，安装误差单独作用下系统两级各行星轮和星轮载荷不均匀系数曲线如图7所示，差动级载荷不均匀系数为1.0255，封闭级载荷不均匀系数为1.0121.

安装误差单独作用下对差动级和封闭级载荷不均的影响不同.差动级各行星轮载荷不均匀系数随时间的变化如图7(a)所示;由于封闭级星轮的旋转中心固定，没有公转，所以安装误差仅改变封闭级各星轮间的载荷分配，各星轮的载荷不均匀系数不随时间变化，如图7(b)所示.

偏心误差和安装误差共同作用下，系统两级各行星轮和星轮载荷不均匀系数曲线如图8所示，差动级载荷不均匀系数为1.0771，封闭级载荷不均匀系数为1.0370，系统两级载荷不均匀系数比图6和图7中偏心误差和安装误差单独作用下载荷不均匀系数大，说明偏心误差和安装误差对系统两级载荷不均匀系数的影响具有累加作用.这一规律符合行星传动均载研究的已有结论，进一步证明了该系统静力学建模的正确性.

由图3-8可见，差动级载荷不均匀系数大于封闭级载荷不均匀系数.载荷越大传动系统越均载［14］，由行星传动理论知，封闭差动人字齿轮传动系统封闭级载荷远大于差动级，所以封闭级载荷分配较为均匀，封闭级载荷不均匀系数对误差变化没有差动级敏感，载荷不均匀系数较小.

图6 偏心误差单独作用下载荷不均匀系数曲线Fig.6 Curves of load sharing factors under action of eccentric errors

图7 安装误差单独作用下载荷不均匀系数曲线Fig.7 Curves of load sharing factors under action of installation errors

图8 偏心误差、安装误差共同作用下载荷不均匀系数曲线Fig.8 Curves of load sharing factors under action of eccentric and installation errors

6 结论

(1)各行星轮/星轮的偏心误差初相角相同情况下，行星轮和星轮的偏心误差变化不会改变系统两级载荷不均匀系数，对系统两级载荷分配没有影响.对于载荷分配均匀性要求高的重要传动系统，装配时可以通过对行星轮/星轮的偏心相位进行选配和调整，使行星轮/星轮偏心误差初相角相同来实现均载.

(2)安装误差对差动级各行星轮和封闭级各星轮载荷不均的影响不同，安装误差引起的差动级各行星轮载荷不均匀系数随时间变化;安装误差仅改变封闭级各星轮间的载荷分配，安装误差引起的封闭级各星轮载荷不均匀系数不随时间变化.

(3)载荷越大传动系统越均载，封闭差动人字齿轮传动系统封闭级载荷远大于差动级，所以封闭级载荷分配比差动级均衡，封闭级载荷不均匀系数对误差变化没有差动级敏感，差动级载荷不均匀系数大于封闭级.

［1］日高照晃，山本信行，石田武.行星齿轮装置均载机构中的各种误差和载荷分配的关系［J］.日本机械学会论文集:C 编，1986，52(480):2200-2206.Hidaka T，Sugimoto N，Ishida T.Effects of errors of elements on load distribution in planetary gears with various load equalizing machanisms［J］.Japanese Mechanical Academic Society Collection:Series C，1986，52(480):2200-2206.

［2］Bodas A，Kahraman A.Influence of carrier and gear manufacturing errors on static load sharing behavior of planetary［J］.JSME International Journal:Series C，2004，l47(3):908-915.

［3］Singh A.Load sharing behavior in epicyclic gears:physical explanation and generalized formulation［J］.Mechanism and Machine Theory，2010，45(3)，511-530.

［4］Kahraman A.Load sharing characteristics of planetary transmisions［J］.Mechanism and Machine Theory，1994，29(8):1151-1165.

［5］Krantz T L.A method to analyze and optimize the load sharing of split path transmissions［R］.San Diego:NASA，1996.

［6］Singh A.Application of a system level model to study the planetary load sharing behavior［J］.ASME Journal of Mechanical Design，2005，127(12):469-476.

［7］Ligata H，Kahraman A，Singh A.An experimental study of the influence of manufacturing errors on the planetary gear stresses and load sharing［C］∥Proc of ASME DETC2007 Conf.Las Vegas:［s.n.］，2007.

［8］Krantz T L，Delgado I R.Experimental study of split-path transmission load sharing［R］.San Diego:NASA，1996:1-9.

［9］肖铁英，袁盛治，陆卫杰.行星齿轮机构均载系数的计算方法［J］.东北重型机械学院学报，1994，16(4):290-295.Xiao Tie-ying，Yuan Sheng-zhi，Lu Wei-jie.Calculative method of load balance coefficient in planetary gear［J］.Journal of Northeast Heavy Machinery Institute，1994，16(4):290-295.

［10］方宗德，沈允文，黄镇东.2K-H行星减速器的动态特性［J］.西北工业大学学报，1990，10(4):361-371.Fang Zong-de，Shen Yun-wen，Huang Zhen-dong.Dynamic characteristics of 2K-H planetary gearing［J］.Journal of Northwestern Polytechnical University，1990，10(4):361-371.

［11］孙智民，沈允文，李素有.封闭行星齿轮传动系统的动态特性研究［J］.机械工程学报，2002，38(2):44-48.Shen Zhi-min，Shen Yun-wen，Li Su-you.Study on dynamic behavior of encased differential gear train ［J］.Chinese Journal of Mechanical Engineering，2002，38(2):44-48.

［12］Parker R G，Lin J.Mesh phasing relationships in planetary and epicyclic gears［J］.Journal of Mechanical Design，2004，126(3):365-370.

［13］孙智民.功率分流齿轮传动系统非线性动力学研究［D］.西安:西北工业大学机械系，2001.

［14］马从谦，陈自修，张文照，等.渐开线行星齿轮传动设计［M］.北京:机械工业出版社，1987:335-337.