泥沙颗粒相对隐蔽度理论分析及其应用

杨文俊，孟 震

(长江科学院水利部江湖治理与防洪重点实验室，武汉 430010)

1 概述

在研究泥沙起动流速时，需要考虑颗粒在床面位置的高低或是否暴露于床面之上，这就出现一个问题，如何定义平均床面(基准面)。为回避这个难题，1965年，长江科学院在四川五通桥茫溪河野外水槽试验中，韩其为等研究人员提出用(绝对)暴露度Δ来表示所研究颗粒在床面的位置(图1(a))。它直接反映了颗粒滚动时力臂的大小，而这个力臂恰好反映了所研究颗粒滚动起动的临界条件和滚动速度，还反映了颗粒起跳时的碰撞效果。Δ愈小表示暴露愈充分，在实际应用中，常用Δ'=Δ/D来表示，即为(二维)相对暴露度［1］。自 Einstein(1950)提出用隐蔽系数概念之后，隐蔽度、暴露度和隐暴度等名称相继出现，其实它们都是表达同一含义。为从物理概念上理解方便，本文尝试对以上名称做一个统一:①暴露度为床面泥沙颗粒在水中的裸露程度;②隐蔽度为由于受其他颗粒的影响，所研究颗粒不能完全暴露在水中的程度。不难推断泥沙颗粒的暴露度大，则其隐蔽度就小，更易起动;反之，若其暴露度较小，则其隐蔽度就大，更难以起动。

图1 不同概化条件下的均匀沙颗粒隐蔽度计算图解Fig.1 Calculation diagram for hidden degree of uniform sediment under different generalized conditions

近50年来，无论是在河流泥沙起动还是在风沙起动研究中，泥沙颗粒相对隐蔽度的应用得到很大发展。但是为研究方便，我国大多研究者都将泥沙颗粒概化为二维“圆饼”模型研究颗粒隐蔽度，即二维泥沙颗粒相对隐蔽度。然而泥沙颗粒实际上多可概化为球体，为研究泥沙颗粒的二维“圆饼”状与三维球状概化对泥沙颗粒隐蔽度的计算有何影响，2011年长江科学院提出了三维泥沙颗粒相对隐蔽度概念［2］。即床面上所研究颗粒的最低点到与下游颗粒接触点或者下游2个颗粒交点之间的一个“虚拟点”之间沿床面的垂向距离(隐蔽长度)与所研究颗粒粒径的比值，记为η，同时可定义ξ=1－η为相对暴露度。不仅如此，2011年长江科学院又提出并解决了受床面坡度影响下的泥沙相对隐蔽度最小值的问题［3］，即非均匀沙隐蔽度的最小值不是从0算起，而是至少从(1－cosθ)/2算起，其中θ为床面坡度，只当θ=0时，相对隐蔽度的最小值才可能取0。下面就基于不同维度的相对隐蔽度、隐蔽度的分布规律等相关研究进行简要阐述。

2 相对隐蔽度研究

2.1 均匀沙相对隐蔽度

如图1(a)所示，D为所研究颗粒直径，O为该颗粒的球心，E为该颗粒沿床面垂向的最低点，J2为与下游颗粒的交点，B为该颗粒与下游颗粒的交点J2在OE线上的垂足，O1和O2为下游颗粒的球心，θ为线OO2与线OE之间的夹角。根据二维泥沙颗粒隐蔽度的定义，可以得出均匀沙隐蔽度η的计算式为

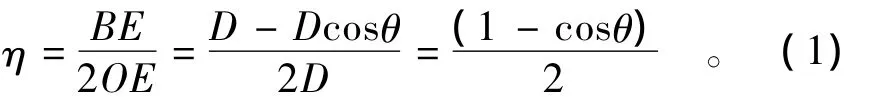
如图1(b)所示，O'是O沿河床垂向在3颗“次表层”泥沙球心 O1，O2，O3所构成平面上的投影，BJ2与线O'O2平行，其余符号含义与图1(a)相同。根据三维泥沙颗粒隐蔽度概念，同样可由式(1)得出均匀沙隐蔽度η，并不难论证π/2］，由此推得该定义下 η的取值区间为［1/2－

根据上述分析，可以发现三维泥沙颗粒隐蔽度在数值上较之经典的二维泥沙颗粒隐蔽度为大。显然，由于在三维模型中，“次表层”颗粒会为所研究的“表层”颗粒提供一个更深的“凹槽”来稳定该颗粒。这里也有必要说明:当泥沙颗粒隐蔽度大于0.5时，则所研究颗粒处于“次表层”，该颗粒不会瞬时起动，在统计意义上，无须研究泥沙颗粒隐蔽度大于0.5的情况。

2.2 相对隐蔽度分布形式

由于缺乏丰富的实测资料检验，泥沙颗粒相对隐蔽度分布形式至今没有得到很好的解决。即便均匀沙相对隐蔽度分布形式也没有一致的结论，非均匀沙隐蔽度分布问题更是未知。对于均匀沙来讲，Paintal、韩其为等一些开创者都认为颗粒隐蔽度在理论上应该符合均匀分布，并把这一假设推广到非均匀沙隐蔽度研究领域中。均匀沙隐蔽度是非均匀沙的特殊情况，目前本文仅能对比较简单的均匀沙颗粒相对隐蔽度的分布问题进行一些讨论。为简单起见，在此以韩其为定义的二维相对隐蔽度为研究对象［3］。

2.2.1 均匀分布

2.2.2 反余弦分布

分析公式(1)，如果理论上认为泥沙颗粒隐蔽度符合均匀分布成立，那么也没有理由否定“角度θ在［π/6，π/2］也有可能符合均匀分布”这一论点。由于颗粒排列是随机的，不同的排列对应不同的角度，若假定角度θ对应的区间上符合均匀分布，即θ的密度函数为

运用概率论不难求出隐蔽度η的密度函数，即

2.2.3 某种正偏态分布

随着水流强度的增大，表层泥沙颗粒所受的水流拖拽力增大，同时“次表层颗粒”也会因受到“表层泥沙”的作用力而发生蠕动(密实度增大)，即“次表层颗粒”之间的“间距”变小，此时“支撑颗粒”所形成的“凹槽”会变小，这必然引起θ的取值范围变小，即促使“表层”泥沙颗粒隐蔽度的减小(暴露度增大，泥沙更容易起动，这一过程也可以用泥沙止动流速小于泥沙起动流速这一事实来理解)。这时泥沙颗粒隐蔽度可以用某一“正偏态分布”(右偏态分布)来描述。事实上，在程年生实验成果的基础上，杨奉广在文献［4］拟合出了二维泥沙颗粒隐蔽度的概率分布曲线(见图2)，其中f(η)=2.309为“泥沙颗粒隐蔽度符合均匀分布”假定下的概率密度函数。

图2 均匀沙相对隐蔽度密度函数Fig.2 Density function of the relative hidden degree of uniform sediment

从图2可知泥沙颗粒隐蔽度的期望稍微偏大于0.186，若采用经典的“均匀分布假设”，可以得出η期望(最值的算术平均)分别为0.283 5(二维)和0.296(三维)。由于几何平均值小于算术平均值，可以用来描述某一“正偏态分布”，若假定泥沙颗粒隐蔽度η的期望用其最值的几何平均来计算，可以分别得到 0.183(二维)和 0.214(三维)。巧合的是，文献［4］反算出的隐蔽度为0.215，三维泥沙颗粒隐蔽度η的期望可近似取其最值的几何平均值，至于隐蔽度准确的分布形式(如比较经典的对数正态分布、瑞利分布等一些正偏态分布)，本文目前还不能给出确凿的结论。

2.3 非均匀沙相对隐蔽度

2.3.1 二维均匀分布

笔者在“均匀分布”假设的基础上，探讨了宽级配非均匀沙任意级配颗粒的二维相对隐蔽度的期望计算式［5］，即

式中:ηi，j为颗粒 Di在颗粒 Dj影响的综合隐蔽度;Pi，j为对应组合的概率;Ni为颗粒Di在表层床沙中的粒数。对于均匀沙，二维相对隐蔽度期望值为0.283 5。

2.3.2 三维正偏态分布

笔者在“某种正偏态”假设的基础上，探讨了宽级配非均匀沙任意级配颗粒的三维相对隐蔽度的期望计算式［2］，即

式中:ηi，j，Pi，j，Ni与式(5)含义相同。对于均匀沙，三维相对隐蔽度期望值为0.214。

无论分析式(5)还是式(6)，均可发现:在宽级配非均匀沙中，粗颗粒的隐蔽度较同等粒径下的均匀沙小;中等颗粒的隐蔽度较同等粒径下的均匀沙相近;细颗粒的隐蔽度较同等粒径下的均匀沙为大。结合宽级配非均匀沙的起动特性，由于人们对宽级配非均匀沙中“大颗粒”、“中等颗粒”、“小颗粒”泥沙的理解不统一，也不能有效地界定。结合本文3.3节的研究，笔者认为在宽级配非均匀沙中:①“大颗粒”为该粒径的泥沙颗粒隐蔽度较之同等粒径条件下的均匀沙隐蔽度为小的颗粒;②“中等颗粒”为该粒径的泥沙颗粒隐蔽度与同等粒径条件下的均匀沙隐蔽度相当的颗粒;③“小颗粒”为该粒径的泥沙颗粒隐蔽度较之同等粒径条件下的均匀沙隐蔽度为大的颗粒。

3 基于相对隐蔽度的泥沙起动研究

3.1 泥沙近底起动流速

相对隐蔽度可以很好地解决底坡和岸坡上的泥沙起动问题，相反地，研究底坡上泥沙起动可以完善相对隐蔽度理论。为简单起见，以研究散体沙为例。

3.1.1 底坡上泥沙起动

泥沙起动流速(切应力)是一个瞬时量，所研究的泥沙颗粒是表层床沙，也就是说所建立的起动流速公式仅仅适合“第一层”床沙。如图3所示，利用经典的受力分析和力矩分析可以容易建立粒径为Di泥沙颗粒绕点Pi滚动起动的力矩平衡方程，进而可以解出底坡上泥沙近底作用起动流速［6］，即

图3 不同底坡上泥沙起动简化模型Fig.3 Simplified model for incipient motion of sediment particles on different bed slopes

式中:CD，CL为拖拽力及升力系数;αD，αL为对应的面积修正系数;α为体积修正系数;Di为所研究的泥沙颗粒粒径;ηi和ξi分别为该颗粒的隐蔽度和暴露度;ubi为所研究泥沙颗粒的近底作用起动流速;kξi为颗粒Di所受水流推力力臂的修正系数，可取0.53。具体推导过程见文献［6，7］。

3.1.2 岸坡上泥沙起动

以往常利用滑动起动模型来研究岸坡上的泥沙起动问题，而采用滚动模型来研究泥沙起动的成果却不多见，主要原因是坡面上泥沙颗粒的转动支点难以确立，而三峡大江截流试验表明岸坡上不少泥沙颗粒是以滚动形式运动的［8］。若假定水流推力方向与坡面平行，并忽略河床纵向下切对岸坡的影响(钱宁观点［9］)，按照滚动起动观点，泥沙起动的原因是促使泥沙起动的动力矩大于阻碍泥沙起动的约束力矩。不妨把阻碍泥沙起动的约束力矩分成2个虚拟分量:x和y方向(如图4示)，当2个促使所研究泥沙颗粒起动的虚拟动力矩的合力矩大于2个虚拟阻力距的合力矩时，认为此泥沙开始滚动(起动)。

图4 单颗粒泥沙受力及力矩分析示意图Fig.4 Forces and moments on single sediment particle

根据图4所示，按照经典的受力分析及力矩分析，不难得到Rx轴向的虚拟动力矩MΣ，y与虚拟阻力距 RΣ，y和 Ry轴向的虚拟动力矩 MΣ，x与虚拟阻力距RΣ，x。当坡度小于时，所研究泥沙的2个“虚拟支点”距床面高程相当，此时可以应用力矩合成原理，建立岸坡上泥沙滚动起动平衡方程:进而可以求出近底作用起动流速，即

式中:kξy为水流推力FD在y方向的分量FD，y的力臂系数;kξx为水流推力FD在x方向的分量FD，x的力臂系数;当坡度不大于时，二者可近似取0.53;ηy表示有坡度的床面上的泥沙颗粒隐蔽度。由于岸坡上“次表层泥沙”受水下重力沿斜面分量的影响，这些颗粒间的排列较平坡床面上紧凑，会引起“表层泥沙颗粒”隐蔽度的期望值较平坡上对应的隐蔽度为小(更容易起动)。对于散体均匀沙来讲，只要岸坡坡度不超过可假定隐蔽度最小值不会发生变化。

3.2 泥沙起动的几个特殊现象

3.2.1 底坡上泥沙起动现象

3.2.1.1 坡度 θ趋于零情况

若床面坡度θ趋于零，则此时式(7)成为

可以利用式(9)论证泥沙起动的几个有趣的现象，如下:

(1)“完全暴露”:如图5(a)所示(ηi→0)，由于此时所研究颗粒Di的隐蔽度ηi趋于零，不难发现

图5 泥沙颗粒几种运动状态示意图Fig.5 Several movement states of sediment particles

这说明当某个颗粒处于“完全暴露”状态时，任何微小流速的水流都可以使该泥沙颗粒起动。同时也表明泥沙颗粒的“个别起动”作为泥沙起动的标准并不合适。

(2)“极限跳跃”:如图5(b)所示(ηi→1)，个别表层泥沙颗粒的隐蔽度ηi趋近1时，水流推力不能有效地促使该颗粒向下游转动，但是由于上游颗粒并不能给予该颗粒有效的“压力”，水流升力(脉动上举力)仍能促使该颗粒以跳跃方式起动［4］，此时上举力系数为某一常数。若把ηi→1代入式(9)可以得到

该式恰好是被广泛采用的平坡床面上泥沙颗粒的跃移起动流速公式。

(3)“完全隐蔽”:如图5(c)所示(ηi=1)，受“粒间作用力”N的影响，认为上举力系数CL趋近于零。把此时的隐蔽度和上举力系数代入式(9)得到

说明“次表层”泥沙颗粒不会起动，参考M.S.Yalin的观点(在相邻颗粒没有他移以前，该颗粒不可能进入运动状态［9］)，可认为“完全隐蔽”的泥沙颗粒处于“自锁”状态。

3.2.1.2 坡角 θ不为零情况

(1)“临界暴露”:当所研究泥沙颗粒隐蔽趋于(1－cosθ)/2 时，将其代入式(7)可以得到

说明当坡面上泥沙颗粒处于“临界暴露”状态时，任何微小流速的水流也可以使该泥沙颗粒起动。不难发现这也说明应用韩其为的宽级配非均匀沙隐蔽度理论在有坡度床面上并不适合。即在研究有坡度床面上泥沙颗粒的隐蔽度时，宽级配非均匀沙隐蔽度的最小值至少为(1－cosθ)/2(平坡时，该值才为零)，同时这是对泥沙颗粒相对隐蔽度理论的一个发展。值得注意的是:国内许多研究者在应用相对隐蔽度来研究底坡上宽级配非均匀沙起动问题时，往往认为隐蔽度的最小值为0，这一错误的观点需要引起同行足够的重视。

(2)“完全隐蔽”:通过对式(7)进行三角函数变换，可以得到另一种等价关系，即

可以证明

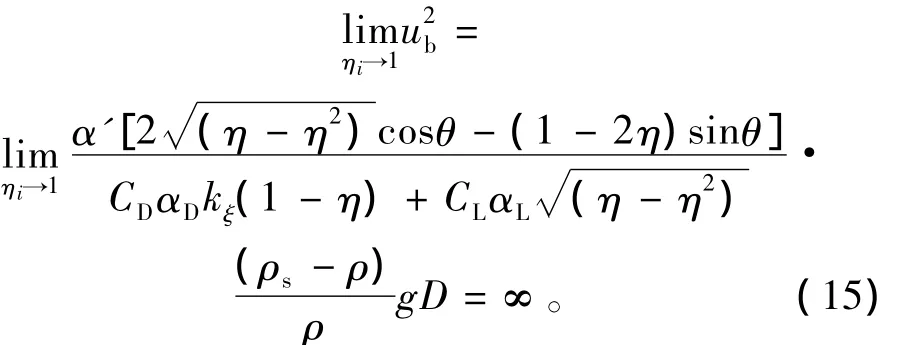
表明无论是否修正上举力系数CL，非平坡床面上的“泥沙颗粒的起动”不可能仅仅是因为上流升力(脉动上举力)与重力沿床面法向分量2种力对比的结果，也即采取跳跃起动模型来研究有坡度床面上的泥沙起动并不太理想。

3.2.2 岸坡上泥沙起动现象

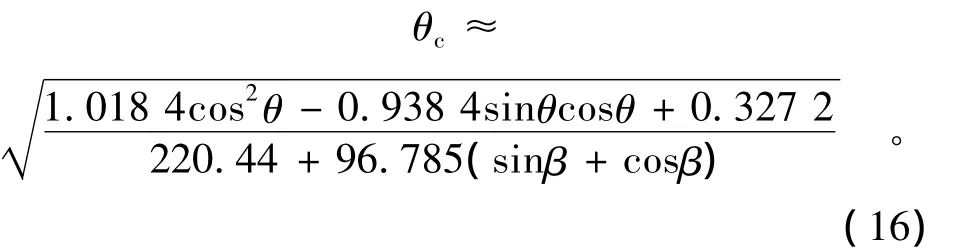
分析上式可以发现(以泥沙颗粒向斜下方滚动为例):

(1)岸坡坡度一般小于泥沙水下休止角，而泥沙水下休止角一般小于45°，当水流的方向固定时，因为可以得到随着岸坡坡度的增大，坡面上的散体沙的起动条件会减小，即容易起动。

(2)岸坡坡度θ固定情况下，当β=π/4时，sinβ+cosβ最大，也即当水流方向与岸坡水平方向呈45°时，岸坡上散体均匀沙起动条件最小，即最容易起动。

3.3 宽级配非均匀沙起动特性论证

对于宽级配非均匀沙起动特性:“大颗粒”较之同粒径的均匀沙易于起动，“小颗粒”较之同粒径的均匀沙难于起动，“中等颗粒”与同粒径的均匀沙起动条件相当。长江科学院在不引进任何“附加动力”、“附加阻力”、“附加质量力”、“等效粒径”等认为人为创造的“虚拟参量”情况下，利用相对隐蔽度从最基本的方程中论证了宽级配非均匀沙的起动特性，这无疑是泥沙颗粒相对隐蔽度在研究泥沙起动研究中的一大特色，证明如下:

若将式(7)对相对隐蔽度η求偏导数可得

这表明对于宽级配非均匀沙来讲，泥沙起动流速是颗粒相对隐蔽度η的增函数;即随着该泥沙颗粒相对隐蔽度η的增大，该颗粒的起动流速也增大。结合式(5)或式(6)不难得出结论:在宽级配非均匀沙条件下，粗颗粒较之同粒径的均匀沙易于起动，细颗粒较之同粒径的均匀沙难于起动，中等粒径泥沙颗粒与同粒径的均匀沙起动条件相当。

同样地，由式(7)对床面坡度求偏导可得

这表明泥沙近底作用起动流速是关于河床坡度的减函数，物理意义为:随着河床坡度的增大，床面上泥沙颗粒的起动流速变小，这与现实也是吻合的。

3.4 Shields带状成因论述

Shields带状曲线反映了诸多学者的研究成果［1］，具有很强的应用价值。Shields曲线表现出的是带状而非一条曲线说明人们对泥沙起动条件的认识存在分歧。我国学者褚君达也分析研究了部分国内学者的研究成果，并绘制了一个表格［10］。他为了统一比较众学者的研究成果，特取近底流速特征高度为泥沙颗粒粒径，即取近底作用流速与摩阻流速的转化关系为 ub=8.5u*(紊流粗糙区)，同样将π/6代入式(7)可以得到

这说明采用不同的隐蔽度值，可以得到相应的散体均匀沙起动条件。特别地，对平坡床面上(θ=0)散体均匀沙而言，式(20)的取值区间变为［0.024 1，0.059 1］，该区间基本涵盖了褚君达对众多学者的统计值［10］，也基本涵盖紊流粗糙区范围内Shields曲线所呈现的数值(如钱宁的统计区间［0.03，0.06］［9］)。

一般来讲，影响泥沙起动条件不同的原因有3种:①起动模型不一，跳跃起动条件明显较大;②起动标准不一(弱动、中动、普动);③近底流速特征高度不一。其中的原因②尤为重要，由于床沙组成特征影响着泥沙颗粒的隐蔽度，所研究泥沙颗粒在不同时刻、不同位置时往往表现出不同的数值，从而导致了在不同起动标准下对应着不同的起动条件，受人们主观因素的影响，会根据相应的实验结果选取不同的起动条件，这便是Shields带状曲线最主要的成因之一。

3.5 泥沙起动条件进一步探讨

根据韩其为的观点(近底作用流速高度取2/3泥沙粒径)［1］，即近底作用流速与摩阻流速的转化关系为 ub=7.49u*［10］，此时式(19)可以转化为

3.6 泥沙水下内摩擦角试验

人们普遍认为泥沙颗粒水下休止角的正切值为泥沙颗粒摩擦系数，即泥沙颗粒水下休止角与内摩擦角相等［10］。若采用滑动起动模型，利用经典的水下受力分析可以容易建立滑动起动平衡方程，进而可以求出滑动起动切应力。同样地取 CD=0.4，θ=0可得当令θci=0.046 9时，可以反算出散体沙颗粒水下休止角为44.52°。而传统的泥沙颗粒水下休止角实验数据均远小于该值［10］。为了解泥沙颗粒水下休止角的数值是否等于泥沙颗粒的摩擦角，笔者进行了泥沙颗粒水下休止角与摩擦角差异化的试验研究。

试验所采用的泥沙为河道中的天然沙，为避免颗粒黏结力的影响，筛选较粗的颗粒，粒径范围为0.9～10 mm。分别筛选出泥沙级配粒径为:①0.9～1.0 mm，② 1.0 ～ 1.25 mm，③ 1.25 ～ 1.43 mm，④1.43 ～1.6 mm，⑤1.6 ～2.0 mm，⑥2.0 ～ 2.5 mm，⑦2.5 ～ 3.2 mm，⑧3.2 ～ 5.0 mm，⑨5.0 ～ 7.0 mm，⑩7.0 ～8.0 mm，[110]～10.0 mm，共11 组。

水下休止角采用传统的抽板法:制作一个有机玻璃水槽(50 cm×20 cm×25 cm)，两端封死，在居其中一端20cm处设置挡板内部填沙，装沙充水完毕后缓慢抽出挡板，沙将在水下重力作用下下滑，形成稳定斜坡，该斜坡坡度为泥沙水下休止角，如图6(a)所示。

图6 泥沙颗粒水下休止角和内摩擦角量测试验Fig.6 Measuring experiment on underwater rest angle and internal friction angle of sediment particles

泥沙颗粒水下内摩擦角反映的是床面上泥沙起动时“表层”泥沙与“次表层”泥沙的摩擦关系。那么在设计试验中特别需要注意两点:其一，如何设定铺沙厚度;其二，如何对床面底部进行铺沙。本次试验在这二点进行初步探索:为解决铺沙厚度问题，引入泥沙颗粒“可动层”概念;为解决床面底部铺沙问题，引入泥沙颗粒“相对隐蔽度”概念。

试验中的铺沙厚度为2倍的粒径(借鉴拜格诺Bagnold床面可动层厚度为1.4倍的粒径和彭凯提出可动层厚度为1.2倍的“起动粒径”［11］)。在第三层“不动层”的铺沙时，“不动层”颗粒间距问题成为难点:过密与过疏均不符合事实，因为第三层的排列将影响次表层的部分“可动层”的稳定性。引用三维泥沙颗粒相对隐蔽度的概念，取均匀沙相对隐蔽度的期望值为0.214，在此基础上经过复杂的初等几何计算，得出第三层“不动层”颗粒间距为 0.420 7倍的粒径，于是根据不同粒径级配的泥沙制作相应的铺凹槽。由于颗粒铺沙间距按照严格的数值，造成小颗粒泥沙铺沙难度非常大，该试验共制作了适用于级配⑥－○11的6块铺沙凹槽。

当铺沙凹槽在水槽内逐步抬高的过程中，可以发现床面上同样存在“弱动”(部分颗粒滚落)、“中动”(床面上某一小片滑落)与“普动”(整个床面上的泥沙一起滑落)的泥沙起动现象。当然在试验的过程中铺沙不会严格平整，受隐蔽度和暴露度因素的影响，存在“个别起动”的假象，可以用肉眼甄别。根据对应的起动标准，锁死拉杆，量测对应的铺沙凹槽坡度，如图6(b)所示。同时也把级配①－⑤的泥沙颗粒放在第6组级配泥沙的铺沙凹槽中进行水下内摩擦角试验。

经过大量重复试验，结合708组试验数据绘制了颗粒水下休止角和内摩擦角的对比曲线(见图7)。可以分析，“中动”摩擦角基本上在44.5°左右摆动，这与反解出的泥沙颗粒内摩擦角是一致的。其中“中动”摩擦角曲线左端的角度较小是因为铺沙厚度过后引起的，这导致“可动层”增大，所得到的内摩擦角向休止角靠近;可以想象:若铺沙更厚(如1 000倍的粒径)，在床面抬高的过程中，所形成临界滑动角度(内摩擦角)将与泥沙颗粒水下休止角趋于一致。该曲线右端角度较大，原因是受尺寸效应的影响，“中动”与“普动”的界限难以分辨，导致其数值较大。该试验的结论为:泥沙颗粒水下休止角小于内摩擦角。原因是在泥沙起动研究范畴中，床沙“不动层”对“可动层”的推移质起到了防滑的作用。在研究泥沙颗粒水下休止角时，由于“可动层”(表层沙)下面的一部分泥沙存在沿斜面的重力分量，这无疑促使斜坡坡度(休止角)变小，这正是泥沙颗粒水下休止角与内摩擦角的本质区别。

4 泥沙相对隐蔽度实验研究展望

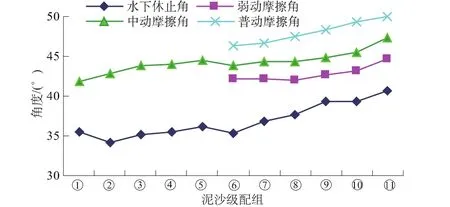
图7 泥沙颗粒水下休止角与内摩擦角差异化对比Fig.7 Difference between underwater rest angle and internal friction angle of sediment particles

综上所述，泥沙颗粒相对隐蔽度对泥沙起动相关的研究具有重要的意义。虽然在理论上可以取得一定的研究成果，但是近50年来，还没有严格的相对隐蔽度物理实验成果，最主要的原因是颗粒排列的随机性以及颗粒形状的复杂性。笔者曾利用长江科学院岩土重点实验室的先进仪器CT进行过相对隐蔽度实验，分别扫描了均匀玻璃球和天然卵石，扫描图片如图8(a)、图8(b)所示;在研究相当对隐蔽度时，把扫描的三维图像剖开为二维图片，见图8(c)、图8(d)所示。虽然由于受处理手段的限制，加上有效的实验图较少，笔者还不能对相对隐蔽度的数据进行有效的采集，但这为隐蔽度的实验研究提供了一种可能性的研究方法。泥沙颗粒相对隐蔽度的实验研究还亟待进一步探索。

［1］韩其为，何明民.泥沙起动规律及起动流速［M］.北京:科学出版社，1999:3－124.(HAN Qi-wei，HE Mingmin.Incipient Characteristics and Incipient Velocity of Sediment Motion［M］.Beijing:Science Press，1999:3－124.(in Chinese))

［2］孟 震，杨文俊.基于三维泥沙颗粒的相对隐蔽度初步研究［J］.泥沙研究，2011，(3):17－22.(MENG Zhen，YANG Wen-jun.Preliminary Analysis on 3-D Hidden Degree of Sediment Particles［J］.Journal of Sedi-ment Research，2011，(3):17－22.(in Chinese))

［3］孟 震，杨文俊.均匀沙相对隐蔽度分布形式研究［J］.人民长江，2011，(16):10－12.(MENG Zhen，YANG Wen-jun.Research on Distribution of Relative Hidden Degree for Uniform Sediment Particles［J］.Yangtze River，2011，(16):10－12.(in Chinese))

［4］杨奉广，刘兴年，黄 尔，等.唐家山堰塞湖下游河床泥沙起动流速研究［J］.四川大学学报(工程科学版)，2009，41(3):84－89.(YANG Feng-guang，LIU Xingnian，HUANG Er，et al.Study on the Incipient Velocity of Tangjiashan Barrier Lake Downstream Area Sediment［J］.Journal of Sichuan University(Engineering Science Edition)，2009，41(3):84－89.(in Chinese))

［5］孟 震，杨文俊.基于二维泥沙颗粒的相对隐蔽度初步研究［J］.长江科学院院报，2011，(5):1－4.(MENG Zhen，YANG Wen-jun.Preliminary Research on 2-D Hidden Degree of Sediment Particles［J］.Journal of Yangtze River Scientific Research Institute，2011，(5):1－4.(in Chinese))

［6］孟 震，杨文俊.基于三维泥沙颗粒相对隐蔽度的底坡上散体沙起动初步研究［J］.泥沙研究，2011，(4):17－22.(MENG Zhen，YANG Wen-jun.Preliminary Research on Incipient Motion Based on 3-D Hidden Degree of Cohesionless Sediment Particles on Bed Slope［J］.Journal of Sediment Research，2011，(4):17－25.(in Chinese))

［7］孟 震，杨文俊.泥沙颗粒相对隐蔽度在散体沙起动研究中的应用［J］.长江科学院院报，2011，(7):1－6.(MENG Zhen，YANG Wen-jun.Application of Hidden Degree to Incipient Motion of Cohesionless Sediment Particles［J］.Journal of Yangtze River Scientific Research Institute，2011，(7):1－6.(in Chinese))

［8］杨文俊，刘力中，郭红民.三峡工程大江截流试验与实践［J］.水力发电，1998，(1):65－68.(YANG Wen-jun，LIU Li-zhong，GUO Hong-min.Test on and Practice of River Closure of Three Gorges Project［J］.Water Power，1998，(1):65－68.(in Chinese))

［9］钱 宁，万兆惠.泥沙运动力学［M］.北京:科学出版社，1983:229－233.(QIAN Ning，WAN Zhao-hui.Dynamics of Sediment Movement［M］.Beijing:Science Press，1983:229－233.(in Chinese))

［10］褚君达.无粘性泥沙的起动条件［J］.水科学进展，1993，4(1):37－43.(ZHU Jun-da.Conditions of Incipient Motion of Non-cohesive Sediments［J］.Advances in Water Science，1993，4(1):37－43.(in Chinese))

［11］冷魁，王明甫.泥沙起动判别标准的研究［J］.人民黄河，1994，(7):1－4.(LENG Kui，WANG Ming-fu.Criteria of Sediment Incipient Motion［J］.Yellow River，1994，(7):1－4.(in Chinese))