SHAPF复合控制策略的改进与仿真研究

谢明磊 廖 明

（广东电网公司梅州供电局，广东 梅州 514021）

随着经济的发展，工业和生活用电中的非线性负荷向电网注入了大量高次谐波电流，严重影响了整个电力系统的安全稳定运行。因此，如何快速有效地滤除电网谐波已经引起了各国学者的普遍关注。

目前，常用的滤波方法有无源滤波和有源滤波两类，其中有源滤波以其优良的性能成为了电网谐波治理的主要研究方向。本文以并联混合有源滤波器（Shunt Hybrid Active Power Filter, SHAPF）为研究对象，介绍了其拓扑和复合控制策略的基础上，针对负荷变化较大时滤波效果受到影响的情况，改进了控制策略并用Matlab软件搭建仿真模型进行了验证。

1 拓扑结构

SHAPF是指有源滤波器与无源滤波器串联之后并入电网的拓扑结构，其结构示意图如图1所示。

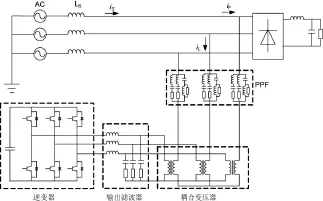
图1 SHAPF拓扑结构示意图

它由无源滤波器、电压型逆变器、输出滤波器以及耦合变压器等4个主要部分组成。其中，无源滤波器采用多个单调谐滤波器组成，主要起到滤除固定次谐波并隔离基波电压的作用，文中由5次、7次单调谐滤波器和二阶高通滤波器并联构成。有源滤波器采用电压型逆变器，输出幅值和相位可调的补偿电流，用以滤除电网中谐波电流并抑制电网阻抗和无源滤波器的谐振。输出滤波器用于滤除逆变器载波频率附近的高频分量，防止高频谐波进入电网。

2 控制策略

SHAPF常用的控制策略大致可分为开环控制[1]和闭环控制[2]，其中常用的开环控制策略是根据负载谐波电流 iLh进行控制，此时系统为前馈控制，动态特性好，无系统稳定性问题，但容易发生欠补偿或过补偿，无法抑制滤波器阻抗与系统阻抗之间的谐振；而常用的闭环控制策略是根据电网谐波电流iSh进行控制，此时系统为反馈控制，能够自我调节补偿效果并抑制串并联谐振，但是系统存在稳定性的问题。因此，为了改善前馈开环调节的准确性和反馈闭环调节的系统稳定性，可采用反馈控制+前馈控制的复合控制策略。即同时检测电网谐波电流iSh和负载谐波电流 iLh，控制逆变器输出电压 uF= K1iLh+ K2iSh。此时系统的主要控制信号来自于 iLh，当其变化时立即对有源滤波器进行相应调节，加速系统响应速度；系统中的反馈控制主要是用来弥补前馈控制的不足，克服因模型不精确所带来的影响，对被控量iSh进行监控调节。

采用输入输出法对图1的系统拓扑进行建模，可得到系统的单相电气模型，如图2所示。

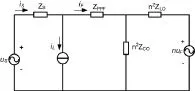
图2 SHAPF的网侧单相电气模型

图中， uS为电网电压， uF为逆变器输出电压，iL为负载电流，ZPPF、ZLO、ZCO分别为无源滤波器阻抗、输出滤波器的感抗和电容支路的阻抗。假设电网电压无畸变，则应用叠加定理，可以得到电网电流中的谐波分量如式（1）所示。

采用复合控制时，将 uF= K1iLh+ K2iSh代入式（1）可得

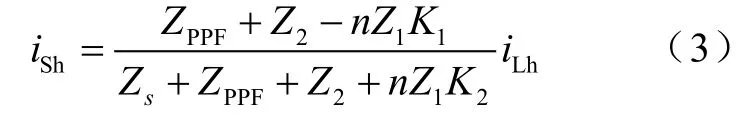
由式（3）可得系统等效电路图，如图3所示。这种控制策略等效为控制有源滤波器来增大电网支路谐波阻抗，同时减小滤波器支路阻抗，从而使大部分谐波“流入”滤波器支路，有效地减少电网电流的谐波含量。

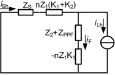
图3 复合控制策略的系统等效电路图

此时可同时调节K1、K2值来获得更好的补偿性能。在相同的滤波要求下，K2能取得更小值，有利于系统稳定。

3 存在问题与改进措施

SHAPF一般采用PWM调制产生uF，其过程如图4所示。

图4 uF控制信号的产生过程

负载电流 iL经过变比为 n:1的电流互感器后进入数字控制器进行谐波计算，得到负载谐波电流后乘以归一化因数μ，去和三角形载波进行比较，产生控制逆变器的PWM调制波。令 iLh表示负载谐波电流，表示经过电流传感器和谐波计算器后的负载谐波电流，如果检测精度足够，则显然有

当非线性负载突然加重，使谐波电流增大较多时，SHAPF控制器检测到的谐波信号乘以归一化参数得到的调制信号会超过载波幅值，从而丢失了部分调制波信息，造成逆变器输出的补偿电流与电网谐波电流有较大误差，影响滤波效果，此时通常改变归一化参数来缩小调制波，但是可以发现滤波效果改善不大。这是因为根据 PWM调制原理，在载波幅值内，逆变器输出电压与调制信号的关系如下

式中，m为载波幅值的倒数，通常取为1，PWM逆变器确定后，m是不变的；电流互感器确定后，变比n一般也是不变的。当为了保证逆变器的谐波调制信号大部分在载波幅值之内，将归一化因数除以一个值时（假设为A），因为直流侧电容电压 udc控制不变，会导致有源滤波器输出容量不足，仅输出iLh/A的补偿电流，无法完全补偿谐波电流 iLh。因此如式（6）所示，还必须改进控制策略，相应增大udc，提高逆变器的输出容量。

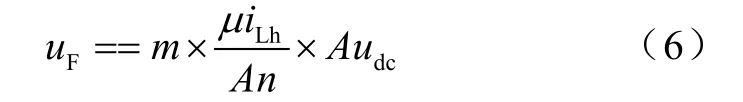
如何合理地改变归一化因数，即确定 A值是改进的控制策略的关键。假设负载改变前的调制波在载波幅值之内，对于不含谐波分量的电流波形，测得负载改变后的基波幅值，按比例减小归一化因数，就可使负载变化后的调制波缩小在载波幅值之内。但是对常用的LC滤波三相不可控整流装置来说，负载不同时，交流侧的电流波形因谐波含量不同而呈不规则变化，因此无法根据上述规则确定归一化因数的改变值。文献[3]给出LC滤波三相桥式不可控整流电路网侧谐波电流的表达式，如式（7）、（8）所示。

式中， X6=6ω L -1/6ωC ，三相不可控整流装置确定后，L、C一般均不改变，即 X6不变；改变的通常是R，它的大小反应负载轻重。

由式（8）可以看出，当系统电压保持不变时，系数 an仅与X6有关； bn仅与R有关。当负载R变化时，基波和各次谐波幅值的增量主要受 bn影响。又基波电流的 b1值与各次谐波电流的 bn值成一定比例，因此可用 b1值变化量来反映 bn的变化量，从而进一步近似反映谐波幅值的变化量。即假设轻载时，逆变器的谐波调制信号大部分在载波幅值之内，测得负载电流 i2的 b1*值；负载加重后，测得此时的 b1值，按 b1/b1*得比例减小归一化因数，即可保证负载变化后的谐波调制信号也在载波幅值之内，减小调制误差。同时 b1/b1*比例增大直流侧电压，就可保证逆变器有足够容量输出相应的补偿电流。

当采用广义dp-dq法检测计算谐波时，通过低通滤波器后得到的直流量如式（9）所示。

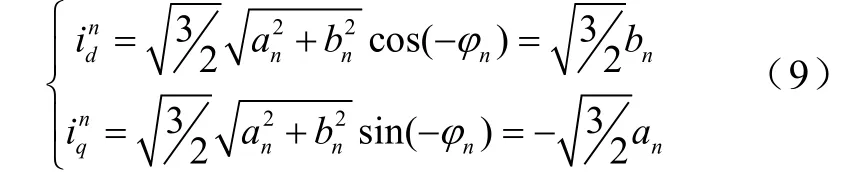
检测低通滤波器处理后的基波有功分量即可很容易得到负载变化前后的 b1值，如式（10）所示。

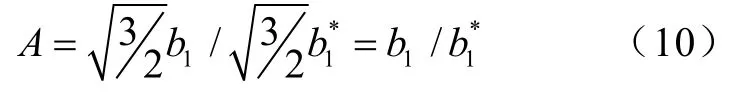
4 仿真实验

用Matlab软件搭建380V低压系统模型进行仿真实验，SHAPF主电路和控制电路的仿真模型分别如图5和图6所示。

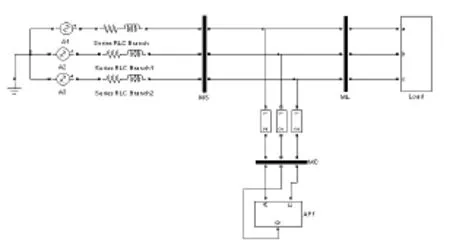
图5 SHAPF仿真模型

谐波源采用 LC滤波的三相不可控整流电路，初始负载为2.5Ω，0.4s增加3Ω。直流侧电容电压初设为350V，负载减轻时，控制策略不会改变电容电压，负载加重时则自动调整归一化因数和直流侧电容电压值，常规和改进控制策略后的滤波效果对比如表1所示。

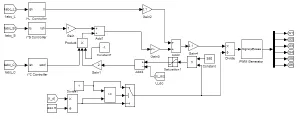
图6 改进的控制策略仿真模型

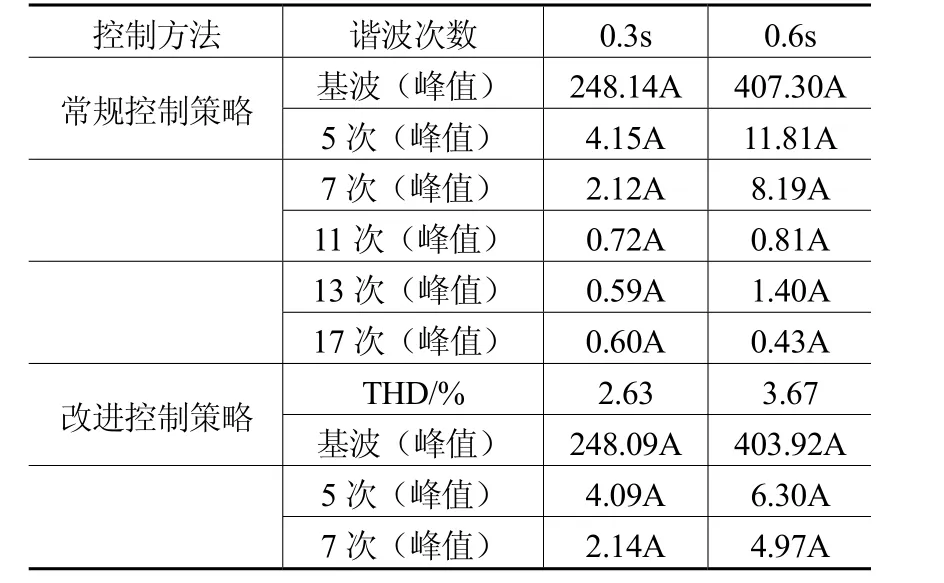
表1 滤波效果比较

从表1中可以看出，当负荷加重时，采用常规控制策略，谐波畸变率增大，滤波效果受到影响，而对控制策略改进后，仍能保持较好的滤波效果。

5 结论

文章在分析了 SHAPF的电路拓扑和控制策略的基础上，针对负荷变化较大时，可能影响滤波效果的情况，提出了改进的方法，并用Matlab软件搭建仿真模型进行了验证，实验结果证明本文提出的改进方法是正确可行的。

[1]BLAJSZCZAK, G Direct method for voltage distortion compensation in power networks by series converter filter. IEE Proc. E.PA., 1995, 142(5):308-312.

[2]朱海平.无变压器混合有源电力滤波器及其控制策略研究[J].通信电源技术,2009,26(6):14-17.

[3]裴云庆,姜桂宾,王兆安.LC滤波的三相桥式整流电路网侧谐波分析[J].电力电子技术,2003,37(3):34-36.