Coupled Vibration of Fluid-filled Functionally Graded Material Cylindrical Shell
(College of Planning and Architectural Engineering,Henan University of Science and Technology,Luoyang 471003,China)
Coupled Vibration of Fluid-filled Functionally Graded Material Cylindrical Shell
LIANG Bin,LI Rong,ZHANG Wei
(College of Planning and Architectural Engineering,Henan University of Science and Technology,Luoyang 471003,China)
The coupled vibration of fluid-filled cylindrical shell based on functionally graded material(FG)is presented.The study is carried out using Love’s thin shell theory.Based on wave propagation method the equation of motion of the coupled system with the fluid effect is derived.By means of conversion switch on axial wave number,the coupled frequency of FG cylindrical shell with various boundary conditions is obtained.Then the frequency of fluid-filled FG cylindrical shell with different boundary conditions is illustrated by examples.The present analysis is validated by comparing results with those in the literature.The results show that the influences of liquids on natural frequencies of fluid-filled FG cylindrical shell are obvious.The effects of axial half wave number,boundary condition and ratio of length to radius on natural frequencies have mainly manifested in the cases of low circumferential wave numbers.
functionally graded materials;cylindrical shell;fluid-filled;natural frequency
Biography:LIANG Bin(1963-),male,professor of Henan University of Science and Technology,E-mail:liangbin4231@163.com;corresponding author:LI Rong(1986-),female,master student of Henan University of Science and Technology.
1 Introduction
FG cylindrical shell is a new kind of compound material structure with component and structure graded distribution along thickness.By using the new kind of functionally graded material,the requirements of special extreme environment such as ultra-temperature,larger temperature gradient and the strong thermal shock on fluid-filled FG cylindrical shell are satisfied.The internal liquid medium and the material properties of functionally graded material have significant impact on the vibration characteristics of cylindrical shell.So the structural analyses of FG cylindrical shell need to be carried out in the presence of liquid.However,since FG cylindrical shell is a group of innovative material structure,the research on the mechanical behavior of fluid-filled FG cylindrical shell is very limited.Since the pioneer work of Junger[1]was published,a lot of theoretical investigations have appeared.The free vibrations of cylindrical shell,filled partially or completely with an incompressible,non-viscous fluid,were discussed by comparative study of shell frequencies to the natural frequency of FG cylindrical shell with various volume fraction law was presented[2-3].The vibration characteristics of cylindrical shell with the impact of the fluid was considered by using wave propagation method[4-6].Sheng[7]presented the report of an investigation for the vibration of FG cylindrical shells with flowing fluid by employing the first-order shear deformation theory.Free vibration analysis of simply supported FG cylindrical shells including thermal effects was performed by Haddadpour[8].Some related researches have been carried out,such as Refs.[9-14].
Based on the Love’s thin shell theory,the equation of motion of the coupled system with the fluid effect is obtained.By means of conversion switch on axial wave number,the natural frequency of fluid-filled FG cylindrical shell with various boundary conditions is derived.By numerical calculations,the coupled frequencies of fluid-filled FG cylindrical shells are discussed.
2 Functionally graded materials
In general,the property of functionally graded material can be expressed as the function of temperature and volume fraction.Based on the temperature coefficients the temperaturedependent material properties are evaluated as follows

where P0,P-1,P1,P2,P3are the coefficients of temperature T(K)and are unique to the constituent materials.We suppose that the material property along the thickness direction of the shell is a function of the constituent materials percentage.

where Viand Voare the volume percentages of the internal and external surfaces of the functionally graded material,respectively.And the expression of Vocan be given as

where Riand R0represent inner and outer radius of the shell,z is the radial distance in the thickness direction,and p is the power-law exponent(0≤p≤∞).Then the definitions of effective mechanical properties such as Young’s modulus E,Poisson’s ratio μ and the mass density ρ can be written as

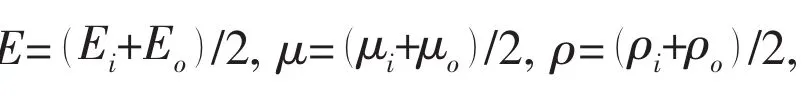
3 Formulation
Consider a cylindrical shell with radius R,length L and thickness h,see Fig.1.The reference surface of the shell is taken to be at its middle surface where an orthogonal coordinate system (x,θ,z) is fixed.The x,θ and z are the axial coordinate,circumferential coordinate and radial coordinate,respectively.
By using Love’s shell theory[9],the equations of motion for a cylindrical shell are obtained.
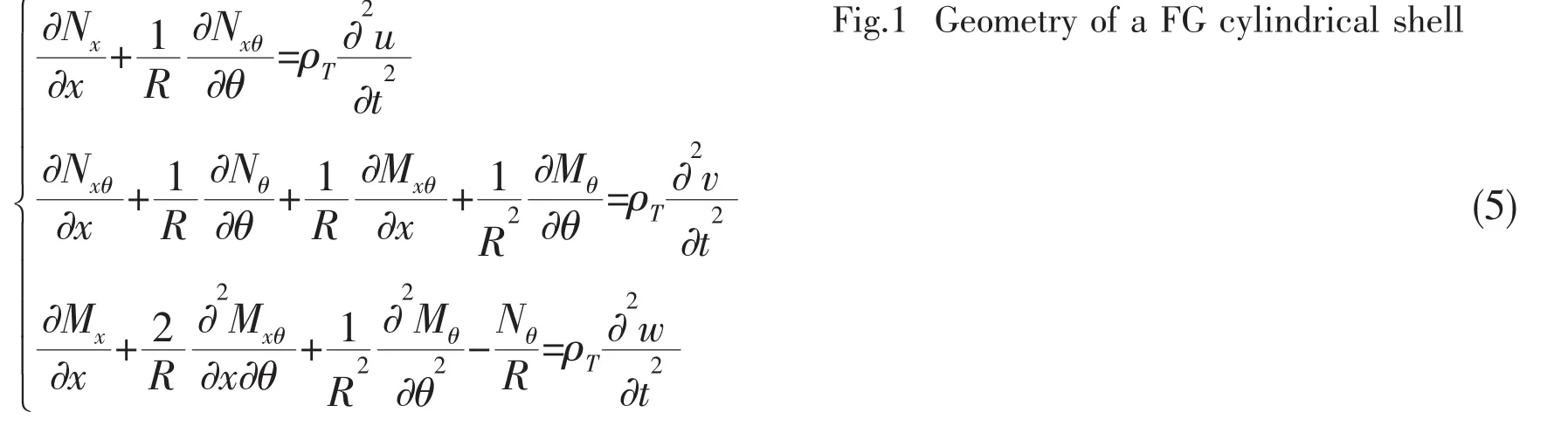
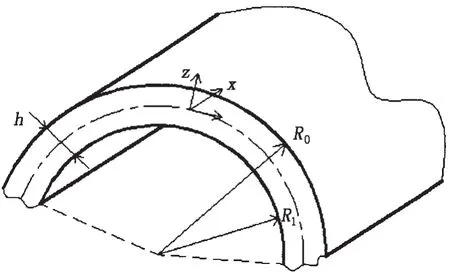
Fig.1 Geometry of a FG cylindrical shell

The displacements of the cylindrical shell can be expressed in the form of wave propagation,associated with an axial wave number kmand circumferential wave number n.

where Um,Vmand Wmare the wave amplitudes in the x,θ and z directions,ω is the natural angular frequency.
The force and moment resultants are related to the strains and curvatures as
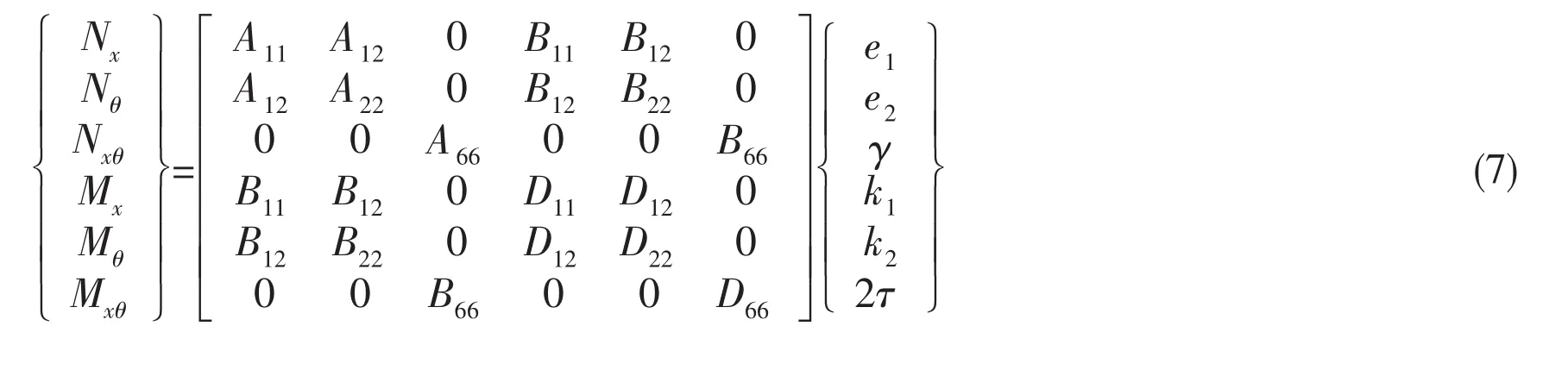
where Aij,Bij,Dij(i, j =1,2,6 )are the extensional,coupling and bending stiffness,e1,e2and γ are the reference surface strains,k1,k2and τ are the surface curvatures.
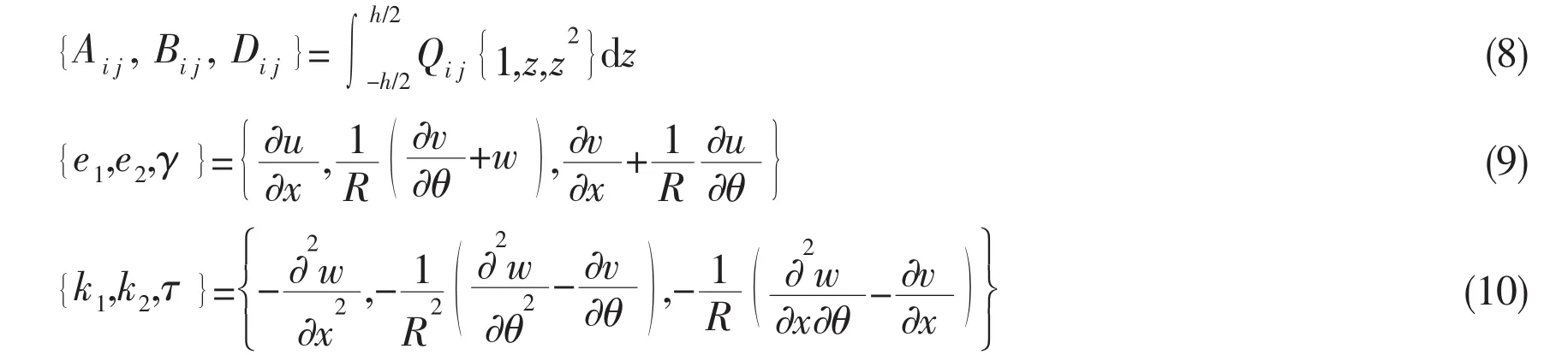
where Qij(i, j =1,2,6 )are stiffness matrix.Because of the isotropy of the functionally graded material,the reduced stiffness can be expressed as
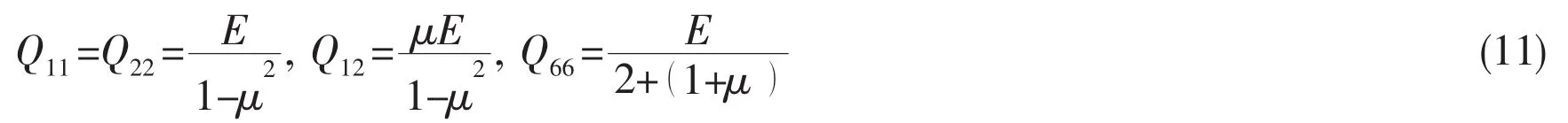
By substituting Eqs.(7)-(11)into Eq.(5),the following equation can be obtained.

where Lij(i, j =1,2,3 )are the differential operators with respect to x and θ.
The fluid exterior of the cylindrical shell is assumed non-viscous which satisfies the acoustic wave equation.The equation of motion of the fluid can be written in the cylindrical coordinate system(x,θ,r ) as

The associated form of the acoustic pressure field exterior of the shell,which satisfies the acoustic wave Eq.(13),is given as

where Jn()is the Bessel function of order n.The relationship between radial wave number krand axial wave number kmis applied to the following.

where Ω is the non-dimensional frequency,CLand CFare the sound speed of the shell and fluid,respectively.The fluid radial displacement and shell radial displacement must be equal at the interface of the shell inner wall and the fluid.This coupling condition is then

where ρFis the density of the contained fluid in the shell,the prime on the Jn()denotes dif-ferentiation with respect to the argument krR.Substituting Eq.(6)into Eq.(12),with consideration of acoustic pressure on the shell and coupling Eq.(17),the equations of motion of coupled system in matrix form can be obtained.
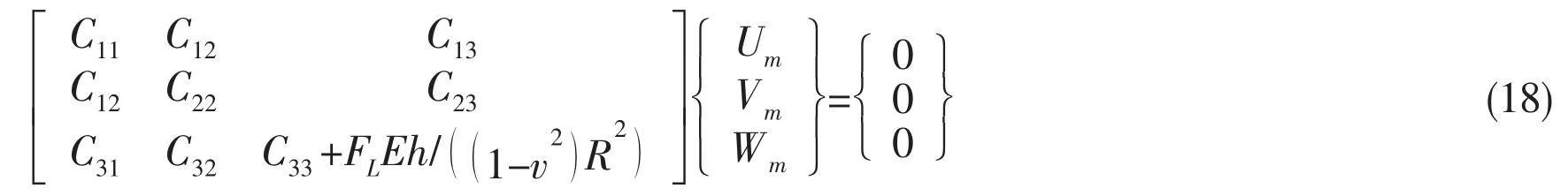
where Cij(i, j =1,2,3 )are the parameters from the Lijafter they are operated with the x and θ,and FLis the fluid loading term due to the presence of the fluid acoustic field.
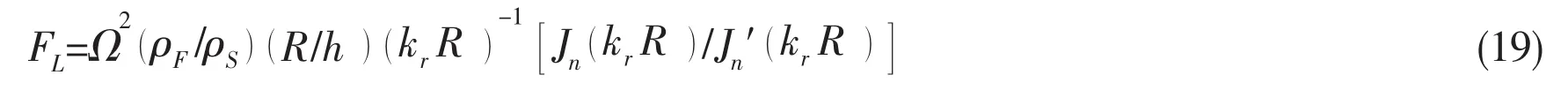
By substituting a boundary condition into kr,the solution of Eq.(18)can be derived.

where both N1(ω ) and N2(ω ) are polynomials of ω.In the case of uncoupled analysis,FL=0.
经病理证实,42例疑似乳腺病变患者中,阳性共计32例,阴性10例;乳腺MR动态增强单一检查中,阳性25例,阴性17例;乳腺MR动态增强扫描联合扩散加权成像检查中,阳性31例,阴性11例。详情见表1。
4 Examples
The natural frequencies of fluid-filled isotropic cylindrical shell with clamped-clamped ends are listed in Tab.1.And the validity and feasibility of the study are verified by comparing results with those in Ref.[4].The geometric parameters of the shell are defined as L/R=20,h/R=0.01,R=1m,p=1.
In this paper,the materials are Stainless steel and Ti-6Al-4V,while the ceramic materials are Si3N4and Zirconia.The material properties are taken into consideration the temperature dependency for the temperature of T=300K as given in Tab.2 from Refs.[10-11].
As an example,natural frequencies with different constituent materials and volume fraction for simply supported ends(S-S),clamped-clamped ends(C-C)and clamped-free ends(C-F)are studied in this paper,see Tab.3,Tab.4 and Figs.2-4.The shells are filled with water of sound speed CF=1 500m/s and mass density ρF=1 000kg/m3.
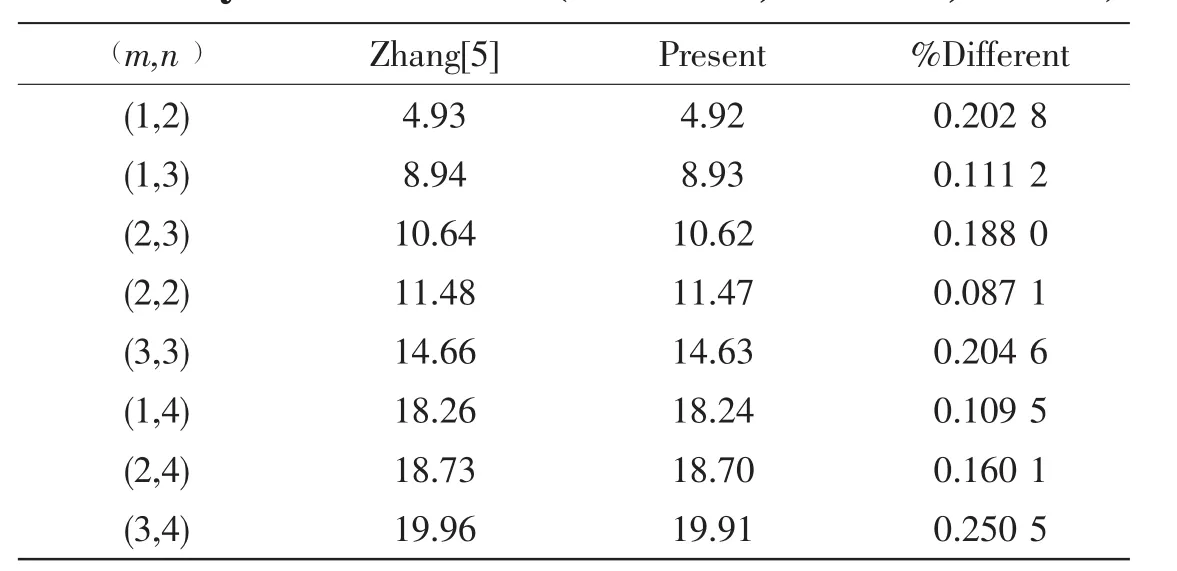
Tab.1 Comparison of natural frequencies for a clamped-clamped fluid-filled isotropic cylindrical shell(h/R=0.01;L/R=20;R=1m)
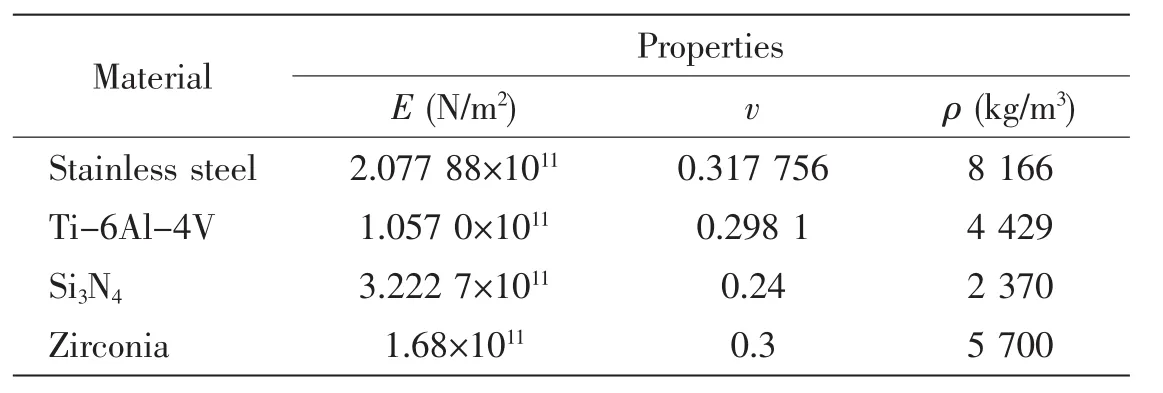
Tab.2 Properties of the functionally graded material components(from Refs.[11-12])
The natural frequencies with different constituent materials for simply supported boundary condition are presented in Tab.3.As can be seen from the table,with the changing of constituent materials,the natural frequencies of the shell change significantly.The coupled frequencies and uncoupled frequencies of FG cylindrical shells first decreased and then increased with circumferential wave number n.
The natural frequencies with different constituent materials for simply supported boundary condition are presented in Tab.3.As can be seen from the table,with the changing of constituent materials,the natural frequencies of the shell change significantly.The coupled frequencies and uncoupled frequencies of FG cylindrical shells first decreased and then increased with circumferential wave number n.
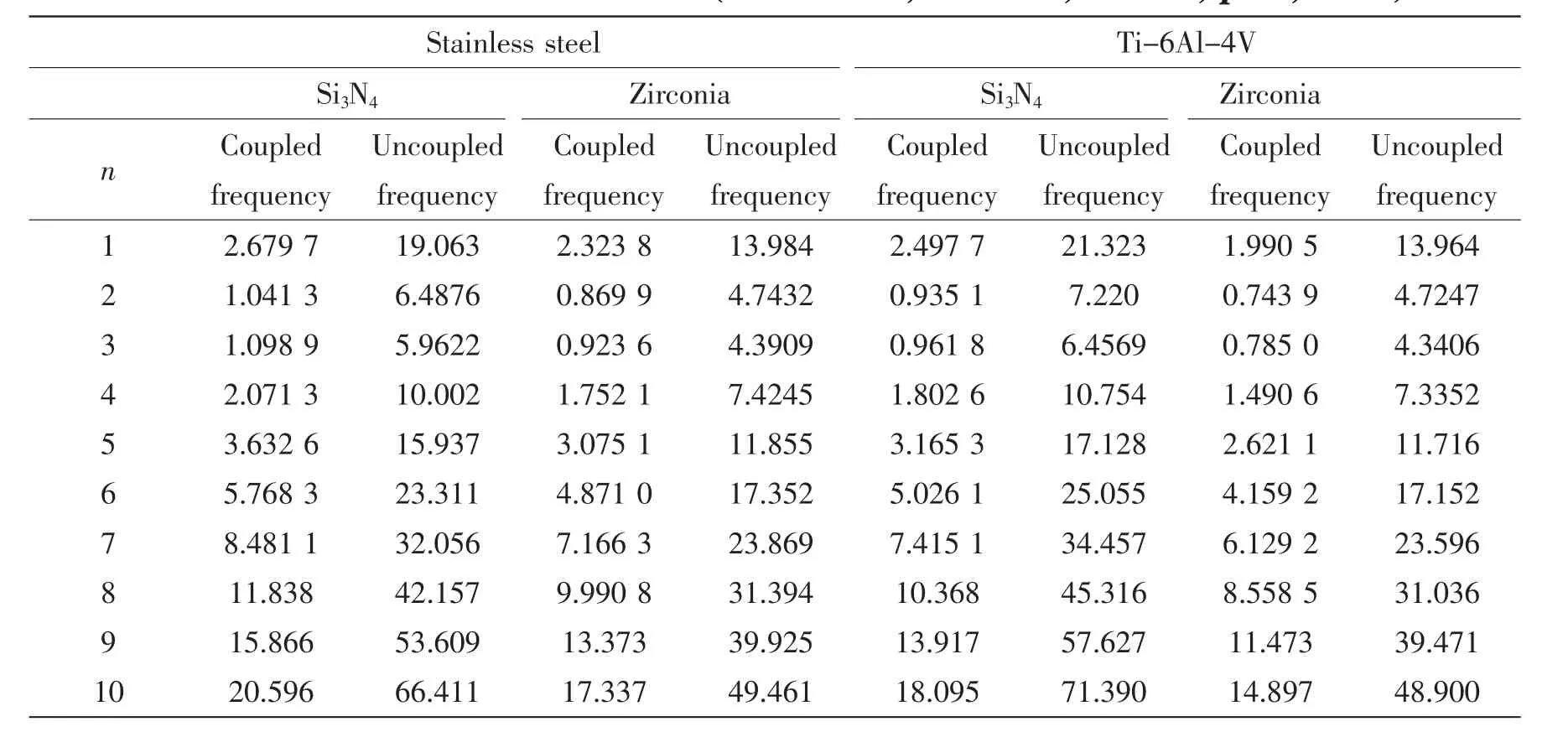
Tab.3 Natural frequencies(Hz)of simply supported FG cylindrical shell for some different constituent materials(h/R=0.002;L/R=20;R=1m;p=1;m=1)
The natural frequencies with different values of volume fraction for simply supported boundary condition are shown in Tab.4.It is shown that when the exponent p comes to a certain degree,the effect of exponent on the volume fraction is not significant.With the decreasing of volume fraction of Stainless steel,the natural frequency of fluid-filled FG cylindrical shell increases gradually.To represent the effect of volume fraction on the natural frequency directly,we take z=0 in this paper.
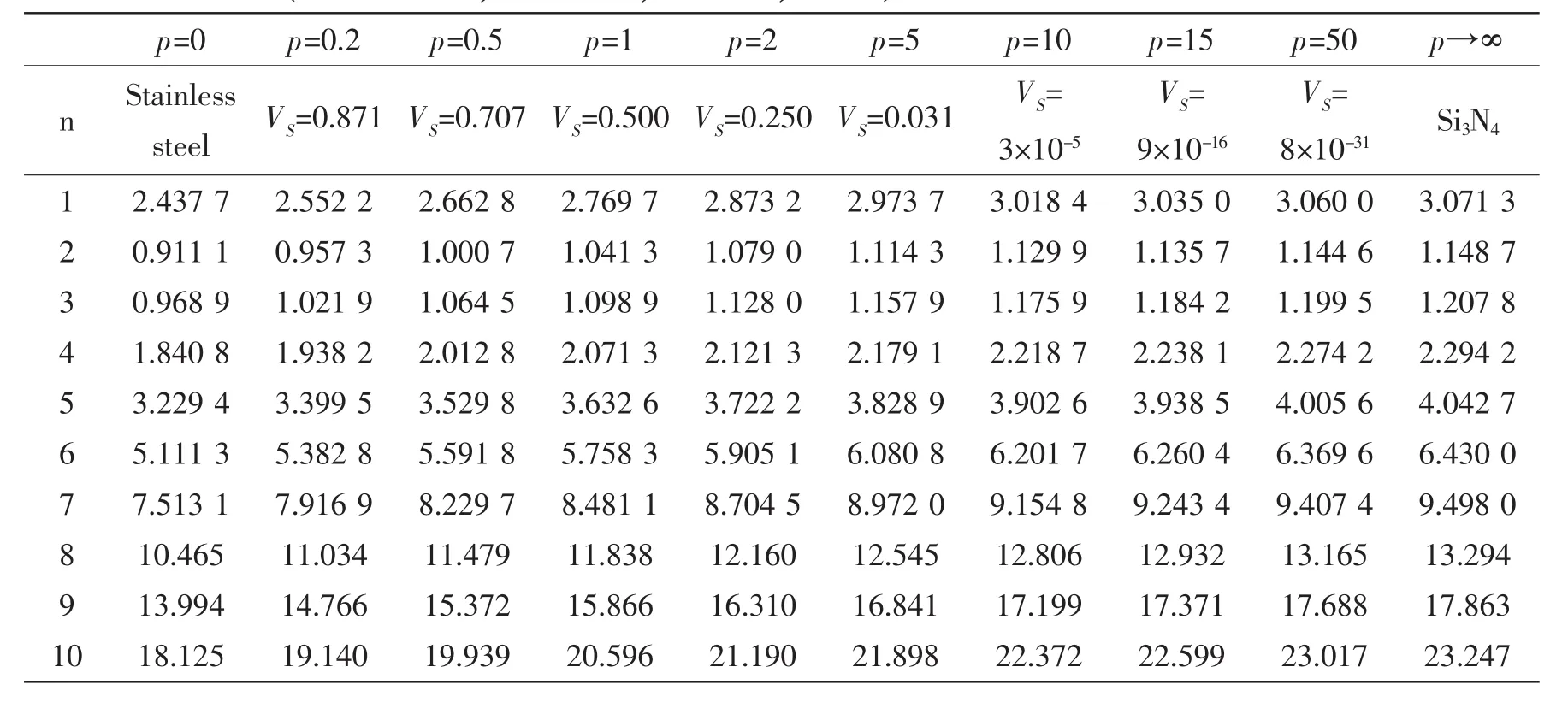
Tab.4 Natural frequencies(Hz)of simply supported fluid-filled FG cylindrical shell for some different values of volume fraction(h/R=0.002;L/R=20;R=1m;m=1)
Fig.2 shows the variations of natural frequencies of FG cylindrical shell and fluid-filled FG cylindrical shell with three kinds of boundary conditions,for the functionally graded material is made up of Stainless steel and Si3N4.It is shown that the fluid effect on natural frequency is significant.Obviously,the coupled frequency is lower than uncoupled frequency.The influence of boundary condition on natural frequencies is mainly reflected in the cases of low circumferential wave numbers.Some parameters are selected as m=1,p=1,h/R=0.002,L/R=20,and R=1m.
The variations of natural frequencies with different constituent materials for three different support conditions are shown in Fig.3.Results given in these figures are obtained by setting m=1,p=1,L/R=20,h/R=0.002 and R=1m.It is shown in these figures that the influence of constituent materials on natural frequencies is evident.The influence of boundary condition on natural frequencies is mainly reflected in the cases of low circumferential wave numbers.The coupled frequencies for clamped-clamped boundary condition are higher than those for simply supported boundary condition,and the coupled frequencies for clampedfree boundary condition are lower than those for simply supported boundary condition.
Fig.4 describes the variations of natural frequencies of fluid-filled FG cylindrical shells for some different axial half wave numbers.It is shown that the influence of axial half wave number on natural frequencies has mainly manifested in the cases of low circumferential wave numbers.With the increasing of axial half wave number,the natural frequency increases gradually.The geometric parameters of the shell are defined as p=1,h/R=0.002,L/R=20,R=1m.
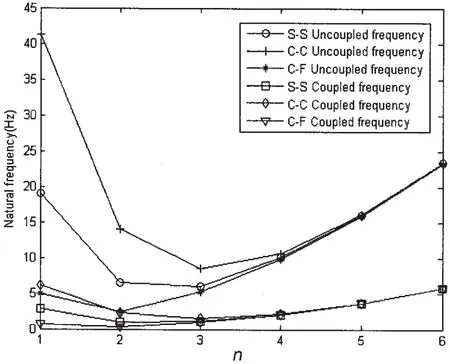
Fig.2 Variation of coupled and uncoupled frequencies of FG cylindrical shells associated with various boundary conditions
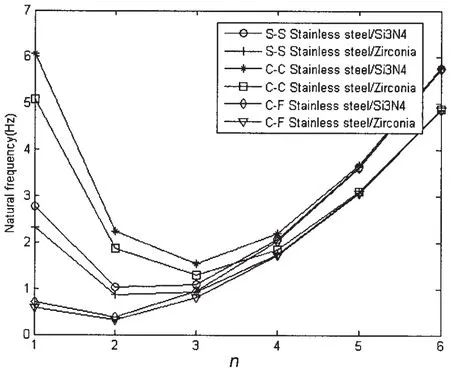
Fig.3 Variation of natural frequencies of fluidfilled FG cylindrical shells for some specified different constituent materials
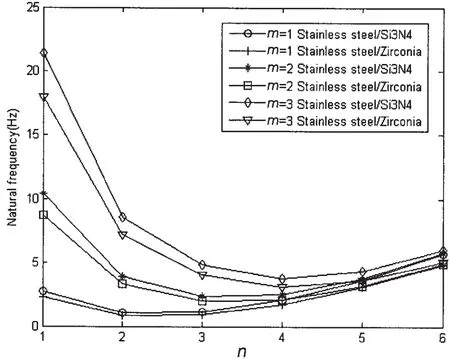
Fig.4 Variation of coupled frequencies of fluidfilled FG cylindrical shells for some different axial half wave numbers
The variations of coupled frequencies of FG cylindrical shells with different L/R ratios are shown in Fig.5.Results given in these figures are obtained by setting m=1,p=1,h/R=0.002 and R=1m.As can be seen from the diagram,the influence of L/R ratios on coupled frequencies is mainly reflected in the cases of low circumferential wave numbers.And the change in natural frequency for small L/R ratios is much greater than for big L/R ratios.
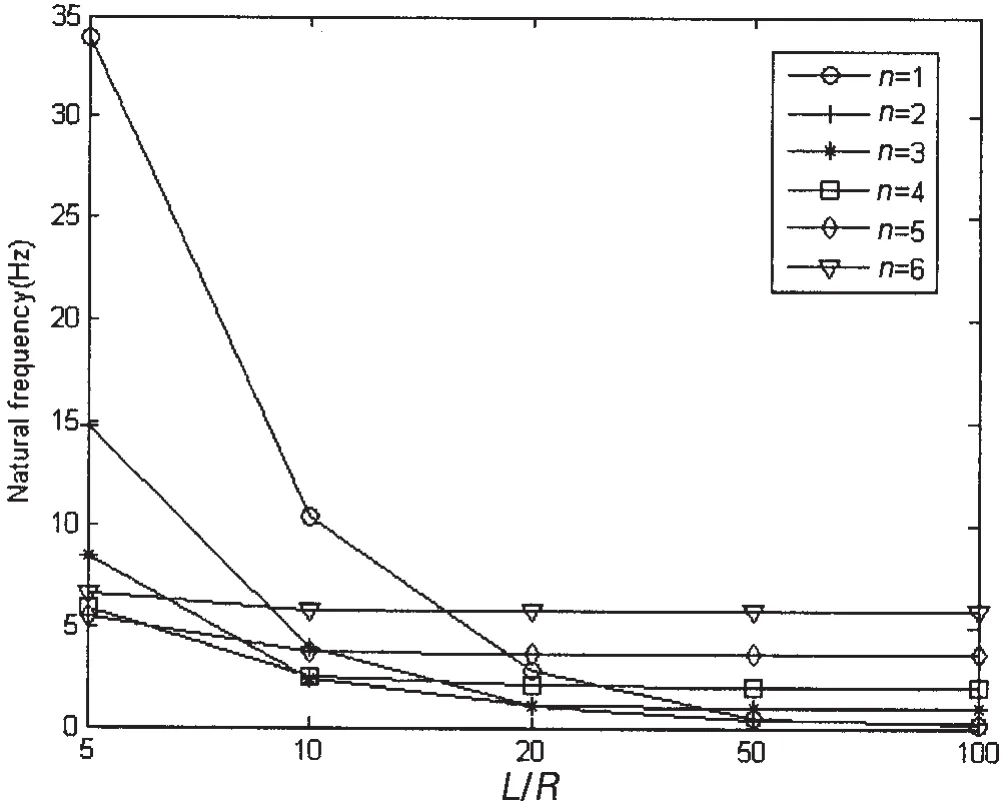
Fig.5 Variation of natural frequencies of simply supported fluid-filled FG cylindrical shells with different L/R ratios
5 Conclusions
In the present paper,the natural frequencies of fluid-filled FG cylindrical shells with three types of boundary conditions are investigated based on the Love’s thin shell theory.To present a relatively comprehensive study,kinds of materials and some specified different values of volume fraction are adopted to describe variations of the natural frequencies.By means of conversion switch on axial wave number,the natural frequency of fluid-filled FG cylindrical shell with various boundary conditions is obtained.Effectiveness of the present work in predicting exact behavior of the shell is checked by comparing its numerical results with the related published results in literature.From the study,some conclusions can be made:
(1)The influence of liquids on natural frequencies of fluid-filled FG cylindrical shell is obvious.The natural frequencies of fluid-filled FG cylindrical shells are lower than those of FG cylindrical shells.
(2)The effects of boundary condition on natural frequencies are mainly reflected in the cases of low circumferential wave numbers.Compare with the simply supported boundary condition,the coupled frequencies for clamped-clamped boundary condition are higher,and the frequencies for clamped-free boundary condition are lower.
(3)The configurations of constituent materials have considerable effect on the natural frequency of fluid-filled FG cylindrical shells.With the changing of constituent materials,the natural frequencies of the shell changes significantly.The coupled frequencies and uncoupled frequencies of FG cylindrical shells first decrease and then increase with circumferential wave number n.
(4)When the exponent p comes to a certain degree,the effect of exponent on the volume fraction is not obvious.With the decreasing of volume fraction of Stainless steel,the natural frequency of fluid-filled FG cylindrical shell increases gradually.
(5)The effects of axial half wave number on natural frequencies have mainly manifested in the cases of low circumferential wave numbers.With the increasing of axial half wave number,the natural frequency increases gradually.
(6)The impacts of ratio of length to radius on coupled frequencies have manifested themselves mainly in the cases of low circumferential wave numbers.And the change in natural frequency for small ratios of length to radius is greater than for big ratios of length to radius.
[1]Junger M C,Mass C.Vibration of elastics shells in a fluid medium and the associated radiation of sound[J].Journal of Applied Mechanics,1952,74:439-445.
[2]Ergin A,Temarel P.Free vibration of a partially liquid-filled and submerged,horizontal cylindrical shell[J].Journal of Sound and Vibration,2002,254(5):951-965.
[3]Arshad S H,Naeem M N,Sultana N.Frequency analysis of functionally graded material cylindrical shells with various volume fraction laws[J].Proc IMechE Part C:Journal of Mechanical Engineering Science,2007,221(12):1483-1495.
[4]Zhang X M,Liu G R,Lam K Y.Coupled vibration analysis of fluid-filled cylindrical shells using the wave propagation approach[J].Journal of Applied Acoustics,2001,62(3):229-243.
[5]Zhang X M.Frequency analysis of submerged cylindrical shells with the wave propagation approach[J].International Journal of Mechanical Sciences,2002,44(7):1259-1273.
[6]Iqbal Z,Naeem M N,Sultana N,Arshad S H,Shah A.Vibration characteristics of FGM circular cylindrical shells containing fluid using wave propagation approach.Applied Mathematics and Mechanics,2009,30(11):1307-1317.(in Chinese)
[7]Sheng G G,Wang X.Thermomechanical vibration analysis of a functionally graded shell with flowing fluid[J].European Journal of Mechanics-A/Solids,2008,27(6):1075-1087.
[8]Haddadpour H,Mahmoudkhani S,Navazi H M.Free vibration analysis of functionally graded cylindrical shells including thermal effects[J].Journal of Thin-Walled Structures,2007,45(6):591-599.
[9]Love A E H.A treatise on the mathematical theory of elasticity[M].4th ed.Cambridge:Cambridge University Press,1952.
[10]Shariyat M.Dynamic buckling of suddenly loaded imperfect hybrid FGM cylindrical shells with temperature-dependent material properties under thermo-electro-mechanical loads[J].International Journal of Mechanical Sciences,2008,50(12):1561-1571.
[11]Kim Y W.Temperature dependent vibration analysis of functionally graded rectangular plates[J].Journal of Sound and Vibration,2005,284(3-5):531-549.
[12]Kwak M K,Koo J R,Bae C H.Free vibration analysis of a hung clamped-free cylindrical shell partially submerged in fluid[J].Journal of Fluids and Structures,2011,27(2):283-296.
[13]Sabri F,Lakis A A.Hydroelastic vibration of partially liquid-filled circular cylindrical shells under combined internal pressure and axial compression[J].Aerospace Science and Technology,2011,15(4):237-248.
[14]Xiang Y,Yuan L Y,Huang Y Y,Ni Q.A novel matrix method for coupled vibration and damping effect analyses of liquid-filled circular cylindrical shells with partially constrained layer damping under harmonic excitation[J].Applied Mathematical Modelling,2011,35(5):2209-2220.
基于功能梯度材料的充液圆柱壳耦合振动研究
梁 斌,李 戎,张 伟
(河南科技大学 规划与建筑工程学院,河南 洛阳471003)
根据Love壳体理论研究了基于功能梯度材料的充液圆柱壳的耦合振动特性。利用波动法,推导出考虑液体影响时FG圆柱壳耦合系统的振动方程。通过变换轴向波数,得到不同边界条件下充液FG圆柱壳的固有频率。与已有文献的分析结果进行对比,验证了文中研究的准确性。研究表明,液体对FG圆柱壳的固有频率有着明显的影响,轴向半波数、边界条件和壳体长度与半径比对固有频率的影响主要表现在周向波数较小的情况下。
功能梯度材料;圆柱壳;充液;固有频率
TB535+.1
A
梁 斌(1963-),男,河南科技大学规划与建筑工程学院教授;
张 伟(1966-),男,河南科技大学规划与建筑工程学院教授。
TB535+.1
A
1007-7294(2011)12-1429-10
date:2011-09-27
李 戎(1986-),女,河南科技大学规划与建筑工程学院硕士生;
- 船舶力学的其它文章
- On Generation of Standardized Load-time Histories and Standardized Load Spectra
- Study of the Prediction of the Engine’s Underwater Exhaust Noise
- Nonlinear Model for Vibration Analysis of Fluid-conveying Pipes via the Incremental Harmonic Balance Method
- Study of Damage Characteristics during Fatigue by Acoustic Emission Techniques
- Comparative Analysis of Vortex Induced Nonlinear Vibration of Casing Pipe under Three Different Boundary Conditions
- Experimental Investigation of Sloshing Loads and Structural Dynamic Responses in Tanks of LNG Carriers

