金属Mo的价键结构随温度和压力的变化
彭红建 ,武青,周姣连,李小波,谢佑卿
(1. 中南大学 化学化工学院,湖南 长沙,410083;2. 中南大学 材料科学与工程学院,湖南 长沙,410083)
价键结构是指固体或分子中原子的价电子结构和原子与原子之间形成的键以及两者之间的关系。研究材料的价键结构有助于从原子结构层次和电子结构层次更深入地了解材料的微观结构,设计出满足人们需要的新材料,也是当今材料设计最为活跃的前沿领域之一[1-6]。确定材料的价键结构主要有2种:第一原理方法和键价法。键价法是在 Pauling电价规则基础上发展起来的,采用与量子力学不同的规则,通过键中求价来确定材料的键价关系。本文作者根据金属材料系统科学框架[7-11],从“能”和“形”2个方面确定价电子结构。能形法[12]是在单原子状态自洽法的基础上将三态杂化扩展为多态杂化,原子杂化状态可连续地变化,其中能量最低的原子状态即为最稳定结构的原子状态,克服两态杂化和三态杂化多解的问题及基本态选择的困难,定出更加精细的原子状态。根据能形法确定金属Mo的价键结构,与第一原理方法和键距差等方法进行比较,并研究其随温度和压力的变化。
1 能形法的原理与方法
金属的价键结构包括价电子结构、键结构和单键半径如图1所示。

图1 BCC体系价键结构的示意图Fig.1 Valence bond structure of BCC-centered cubic crystal
根据晶格常数(式(1))和结合能(式(2))便可计算金属的晶格常数和结合能。
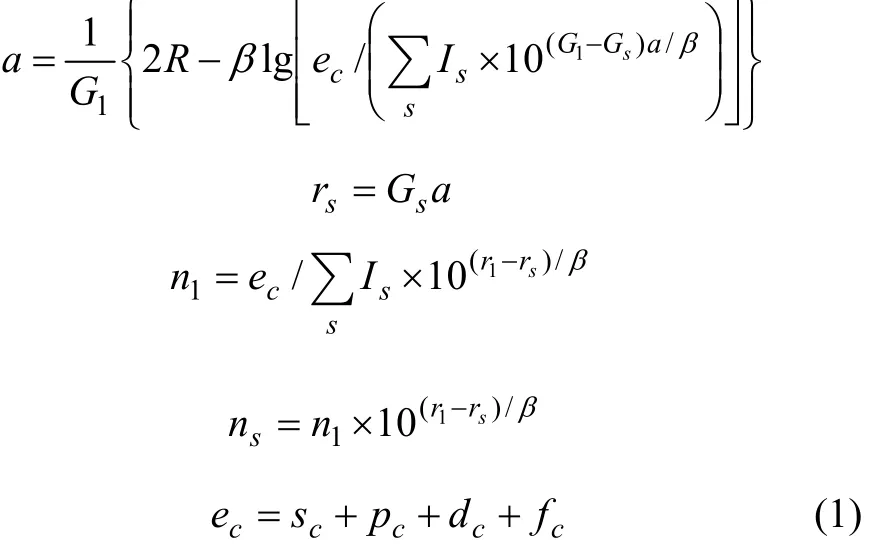
式中:ec为杂化原子的共价电子数,sc为 s轨道共价电子数;pc为 p轨道共价电子数;ef为杂化原子的自由电子数;a为晶格常数;s代表不同键的类型(1代表最近邻键,2代表第二近邻键,3代表第三近邻键,…);ec和R分别为杂化原子的共价电子数和单键半径;rs,Is和ns分别为各类键的键长、等同键数和键价;Gs和Is为与晶格类型相关的常数;β按EET理论取值。对于fcc和bcc晶体结构,仅考虑原子的近邻、第二近邻和第三近邻的相互作用。
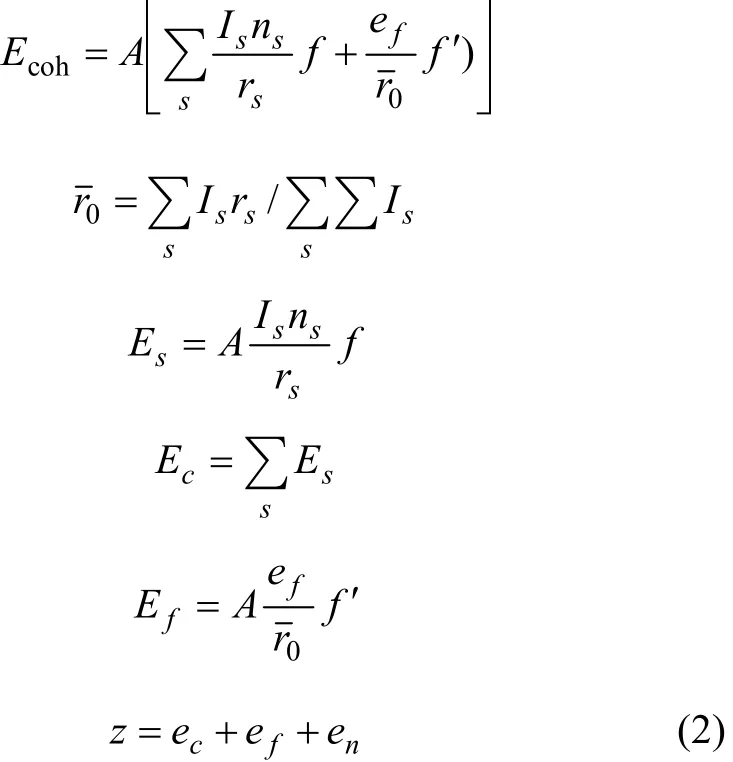
式中:A表示原子中电子电荷对核电荷的屏蔽常数,由于原子内层电子的屏蔽、电子的库仑、交换及关联作用对键能影响的总效应,它是一个与元素相关的量,其值通过晶体结合能的实验值来定;z是原子外层电子总数;f 和 f´分别表示共价电子和近自由电子的成键能力,它与价电子的关系为:
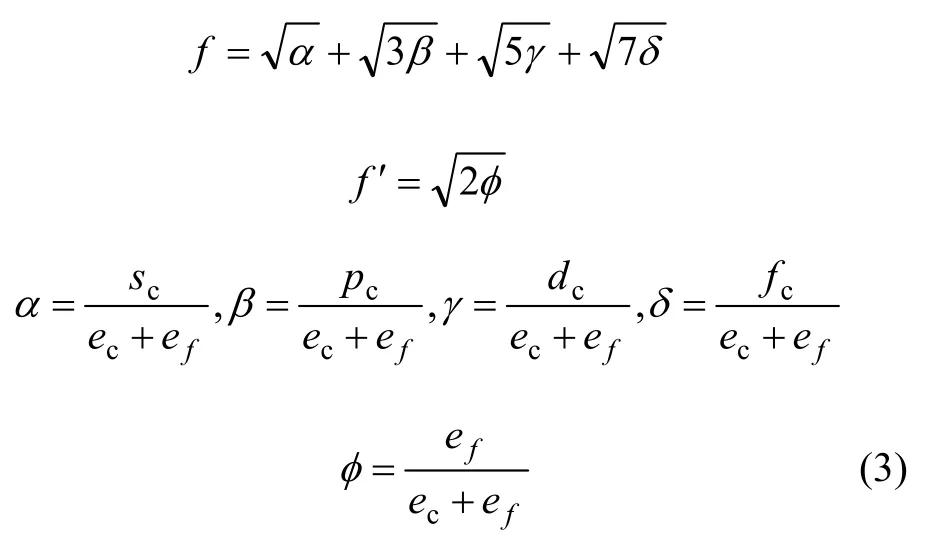
任意温度T下的平衡晶格常数为:

其中:a293为293 K时的晶格常数;α为线热膨胀系数。
对于随压力的变化采用 Rose物态方程[13],其函数表达式采用如下形式:
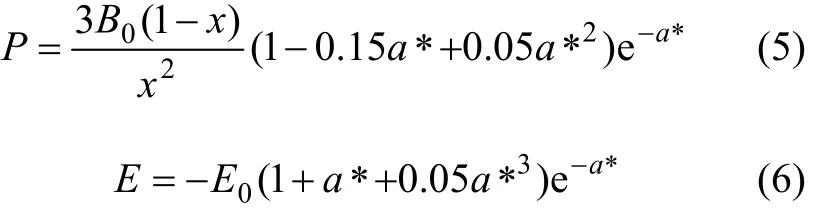
其中:

B0,V0和E0分别是零温零压下体弹性模量、原子体积和结合能,从式(5)可知压力与晶格常数的关系。
2 金属Mo的价键结构
从金属Mo的外层电子结构来看,约4.910 4个(平均数)共价电子用来形成具有定域特征的共价键,1.089 6个(平均数)近自由电子用来形成具有离域特征金属键,这与金属导电性和硬度极其相关;由于原子轨道的d-s-p杂化,约1.650 0个(平均数)的d或者s轨道电子升级到p轨道以形成更强的共价键。
从能量分配来看,金属的结合能主要来源于近邻和次近邻原子的相互作用所形成的共价能,共价电子形成的共价能为634.366 3 kJ/mol,但近自由电子所形成的自由能为23.972 4 kJ/mol,也是一种不可忽视的能量。对于金属Mo外层价电子数有很多,但只有一种的能量是最低的,相对结合能随sc和pc电子占居数的变化如图2所示,因此,可以确定最稳定状态的sc和pc电子占居数。
对于Mo的价态,Pauling将它的价定为6;Raju[15]则认为是ds杂化,将其价态定为4d55s1,与自由原子相同;能形法将 Mo定为固定价 4.910 4,流动价1.089 6,其总价等于6.000 0;Mulliken方法计算金属Mo的原子价轨占居数,外层电子的值为键或离域成键,又不能计算,因为第一原理是按能量的高低填充电子,因此,可以看出能形法能更精细地确定价电子结构。
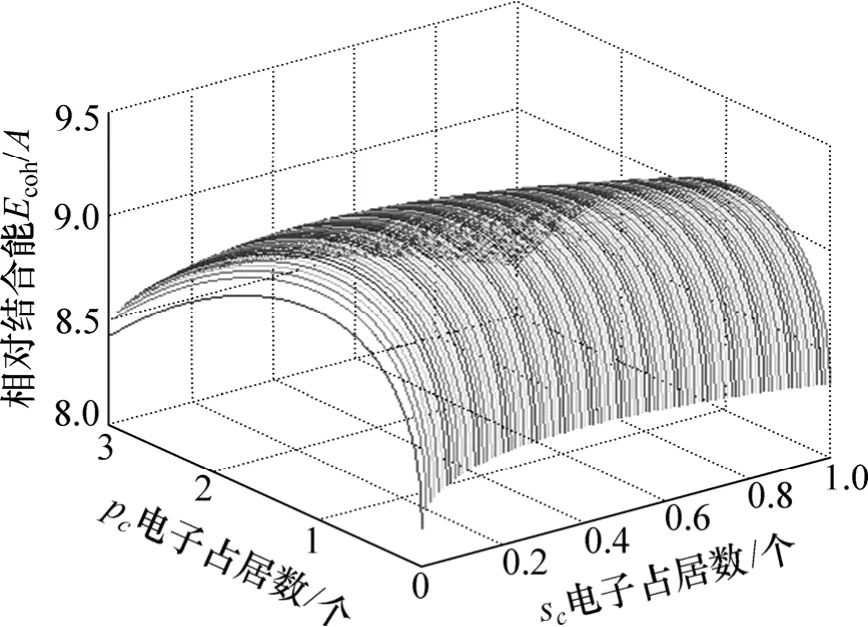
图2 金属Mo的相对结合能随sc和pc电子占居数的变化Fig.2 Relative cohesive energy of Mo with sc and pc electrons
另外,键距差[15](BLD)法确定金属 Mo价电子结构为哑对电子数nd(0.761 4),共价电子数nc(4),晶格电子数nl(1.238 6),总价电子数nT(5.238 6),单键半径R(0.123 78 nm)。BLD法是元素2个极限价态之间的某一离散价态,该价态的晶格常数与实验晶格常数之差小于等于0.005 nm。由能形法所得无素价态是元素所有可能的价态中,与实验晶格常数和结合能相差最小的价态。相比BLD法,能形法增加了“能”的判据。
对于单键半径,Pauling的单键半径为0.129 6 nm,计算值为0.128 08 nm。比较小的原因主要有2个:一是 Pauling只考虑了原子的近邻相互作用,能形法不仅考虑近邻原子的相互作用,而且考虑第二近邻、第三近邻原子的相互作用等;二是近自由电子对共价键的键长不起作用,由于它的存在导致共价电子数减少。
3 金属Mo的价键结构随温度的变化
金属Mo的价键结构随温度变化关系如图3所示。其中:金属 Mo价电子结构(dc,sc,pc,ec和 ef)随温度变化如图3(a)所示;单键半径(R)和晶格常数(r2)随温度变化如图3(b)和3(c)所示;最近邻键长(r1)及键价(n1)随温度变化如图3(d)和3(e)所示;结合能(Ecoh)、相对结合能(Ecoh/A)及屏蔽常数A随温度变化如图3(f),(g)和(h)所示。
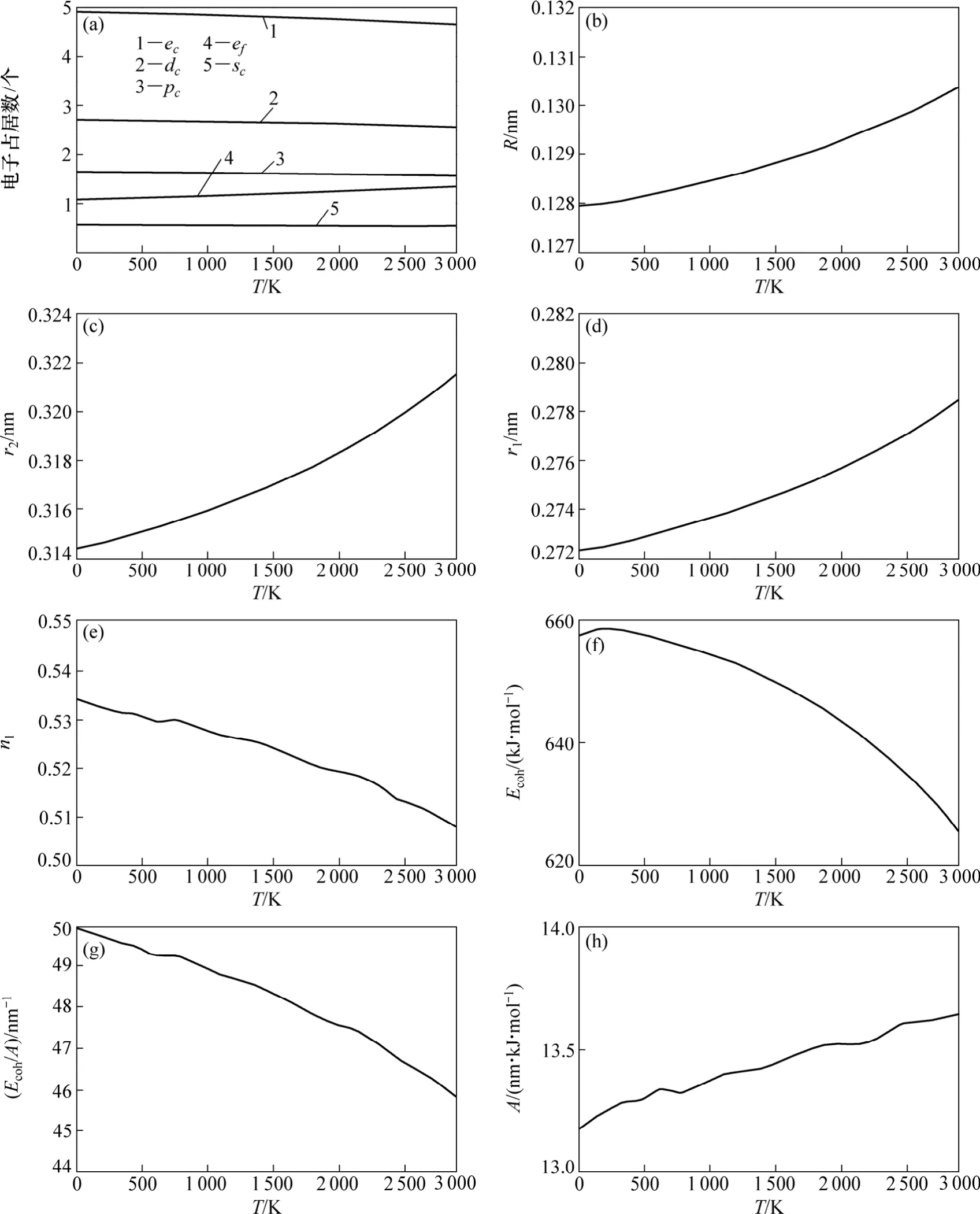
图3 金属Mo的价键结构与温度的关系Fig.3 Relationship between valence bond structure of Mo metal and temperature
从图 3(a)可以看出:随着温度升高,共价电子ec(sc,pc,dc) 减少,近自由电子ef增多,但在固相范围内变化不大;图3(b)和(c)说明了键长与温度的关系,键长随温度的升高而增大。图3(d)和(e)说明了最近邻键长与其键价的相互关系,可见:随着温度升高,键长增长,键价降低;图3(f),(g)和(h)说明了键能与温度的关系,发现随着温度升高,键长变长,键价减少,即键上电子对数减少,键能也降低。这是成键电子减少、原子间距变大造成的。
4 金属Mo的价键结构随压力的变化
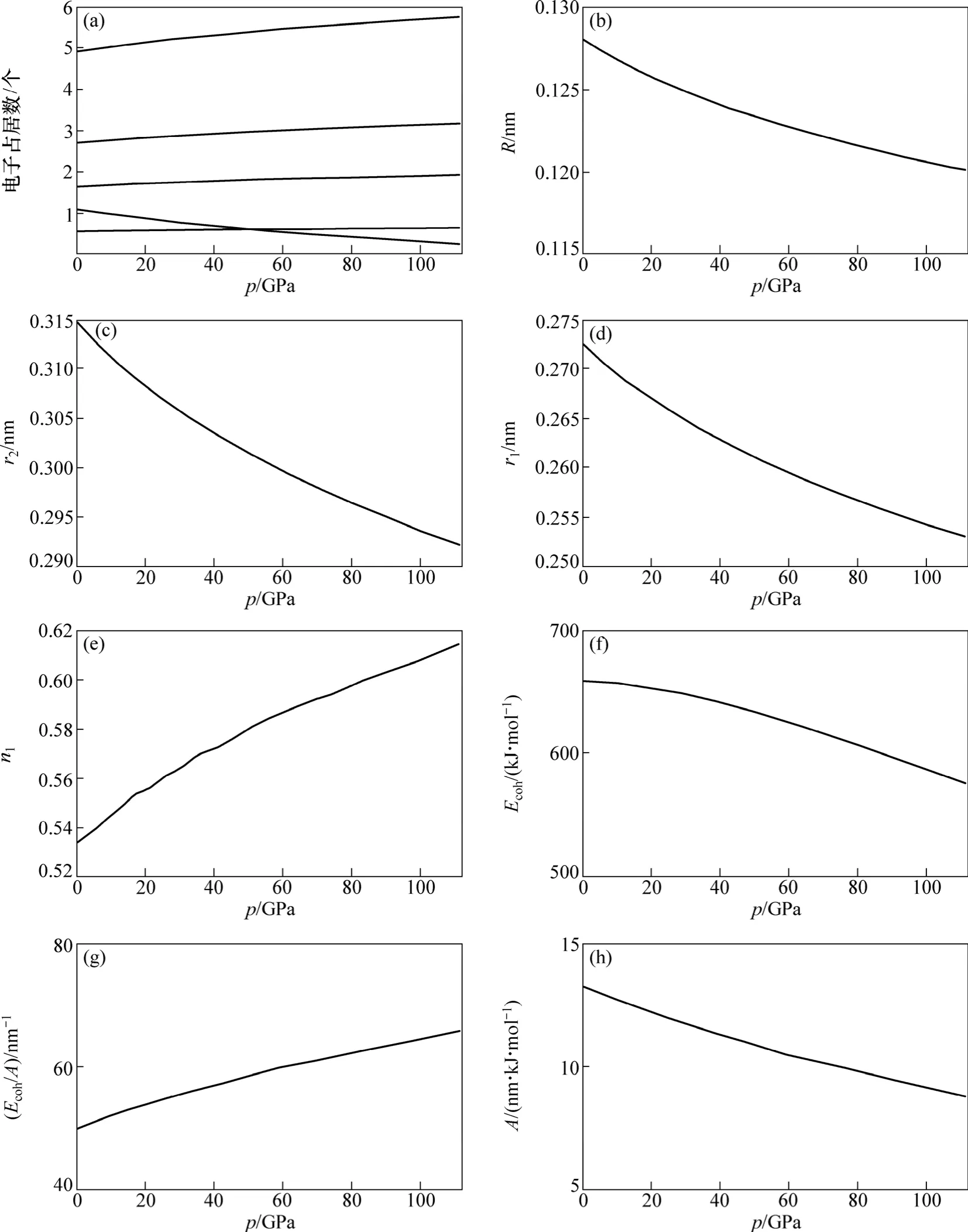
图4 金属Mo的价键结构与压力的关系Fig.4 Relationship between alence bond structure of Mo metal and pressure
根据式(5)和(7)及Rose在文献[14]中确定3个参数B0,V0和E0,可以确定金属Mo的价键结构随压力变化如图4所示。其中:金属Mo价电子结构(dc, sc, pc, ec和ef)随压力变化如图4(a)所示;单键半径(R),晶格常数(r2)随压力变化如图4(b)和4(c)所示;最近邻键长(r1)及键价(n1)随压力变化如图 4(d)和 4(e)所示;结合能(Ecoh),相对结合能(Ecoh/A)及屏蔽常数A随压力变化如图 4(f),(g)和(h)所示。
从图 4(a)可以看出:随着压力的增大,金属 Mo的共价电子数ec(sc,pc,dc)增多,近自由电子数ef减少;在压力0~130 GPa范围内,压力对价电子结构影响显著,其表现金属性下降,共价性增加。图(b)和(c)说明了键长与压力的关系,单键半径随压力的增大而减小。图4(d)和(e)说明了最近邻键长与其键价的相互关系,可见键长变短,键价增加,即键上电子对数增加。图4(f),(g)和(h)说明了键能与压力的关系,可见压力增大,结合能降低。这是外界做功转化为内能的缘故。在整个压力范围内,结合能变化还是很大,相对结合能与压力呈单调递增关系,这是成键电子增加、原子间距变小造成的。
通过结合能和相对结合能可以定出屏蔽常数,屏蔽常数与压力呈单调递减关系,因此,温度和压力对结合能的影响机理是不一样的,结合能的变化是相对结合能和屏蔽常数相互作用的结果。当温度变化时,相对结合能的减少量超过屏蔽常数的增大量,导致结合能降低;而压力变化时,相对结合能的增加量小于屏蔽常数的减少量,导致结合能降低。
5 结论
(2) 随着温度升高,共价电子减少,近自由电子增加,但在固相范围内变化不大;随着温度升高,键长增长,键价降低,键能也降低。
(4) 随着压力的升高,共价电子增加,近自由电子减少,晶体的共价性增加,金属性下降,且键长缩短,键价增大,键能降低。
[1] Brown I D. The chemical bond in inorganic chemistry: the valence bond model[M]. New York: Oxford University Press,2002.
[2] Brown I D. Influence of chemical and spatial constraints on the structures of inorganic compounds[J]. Acta Cryst. B, 1997, 53:381-393.
[3] Hunter B A, Howard C J, Kim D J. Bond valence analysis of tetragonal zirconias[J]. J Solid State Chem, 1999, 146(2):363-368.
[4] Swenson J, Adams S. Application of the bond valence method to reverse Monte Carlo produced structural models of superionic glasses[J]. Phys Rev B, 2001, 64(2): 024204(1-10).
[5] Adams S, Swenson J. Bond valence analysis of reverse Monte Carlo produced structural models; a way to understand ion conduction in glasses[J]. J Phys: Condens Matter, 2005, 17(5):S87-S101.
[6] Urusov V S. Semi-empirical groundwork of the bond-valence model[J]. Acta Cryst B, 1995, 51: 641-649.
[7] 陶辉锦, 谢佑卿, 彭红建, 等. 面心立方和亚稳液相金属 Cu的电子结构和物理性质[J]. 中南大学学报: 自然科学版, 2007,38(1): 1-8.TAO Hui-jin, XIE You-qing, PENG Hong-jian, et al. Electronic structures and physical properties of FCC and metastable liquid Cu metals[J]. Journal of Central South University: Science and Technology, 2007, 38(1): 1-8.
[8] PENG Hong-jian, XIE You-qing, NIE Yao-zhuang,Thermodynamic properties of stable and metastable phases of Pt metal[J]. Tans Nonferrous Met Soc China, 2009, 19(2):428-432.
[9] XIE You-qing. The electronic structure and properties of pure iron[J]. Acta Metall Mater, 1994, 42(11): 3705-3715.
[10] 彭红建, 谢佑卿, 李小波. 单原子状态自洽法的算法[J]. 中南大学学报: 自然科学版, 2007, 38(5): 900-905.PENG Hong-jian, XIE You-qing, Li Xiao-bo. Algorithms of single-atom self-consistency method[J]. Journal of Central South University. Science and Technology, 2007, 38(5): 900-905.
[11] LI Xiao-bo, XIE You-qing, NIE Yao-zhuang, et al. Energy and shape method for determining the valence and bond structure of crystals[J]. Physica B, 2007, 391(2): 249-255.
[12] Rose J H, Smith J R, Guinea F, et al. Universal features of the equation of state of metals[J]. Phys Rev B, 1984, 29(6):2963-2969.
[13] Gray D E. American Institute of Physics, American Institute of Physics Handbook[M]. 3rd ed. New York: McGraw-Hill Book Company, 1972: 23-24.
[14] Raju S, Mohandas E, Raghunathan V S. Engel-brewer electron correlation model: A critical discussion and revision of concepts[J]. Mater Trans JIM, 1996, 37(3): 195-202.
[15] 张瑞林. 固体与分子经验电子理论[M]. 长春: 吉林科学技术出版社, 1993: 255-257.ZHANG Rui-lin. The empirical electronic theory of solids and molecules[M]. Changchun: Jilin Science and Technology Press,1993: 255-257.
- 中南大学学报(自然科学版)的其它文章
- 有菌和无菌体系下磁黄铁矿氧化的电化学研究
- 3株细菌降解木质素的条件调控研究

