大跨度悬索桥的静风稳定性分析

黄传岳 上海铁路局宁波工务段

1 概述

随着现代交通的发展，往往需要修建穿越大江大河、海湾海峡的结构，大跨度悬索桥是满足这种需要的优秀结构形式。目前世界上跨径超过1 100 m的桥梁都是悬索桥，已经建成的日本明石海峡大桥的主跨为1 991 m，而规划中的我国琼州海峡大桥的主跨达到了3 500 m。悬索桥是一种柔性结构，随着悬索桥跨径的不断增大，其最关键的问题就在于设计风速下的气动稳定性。

空气静力失稳是指结构在给定风速作用下，主梁发生弯曲和扭转，一方面改变了结构刚度，另一方面改变了风荷载的大小，并反过来增大结构的变形，最终导致结构失稳的现象。相对于动力失稳现象，桥梁静力失稳突发性更强、破坏性更大。过去，人们普遍认为颤振临界风速一般低于静力失稳风速。Boonyapinyo、Miyata、谢旭、方明山等学者通过计算发现了静风失稳现象出现的可能性。因此，有必要对大跨度桥梁的静风稳定性问题进行全面的研究。

2 静风荷载的计算

静风荷载是指作用在桥梁结构上气动力中的定常部分，如图1按主梁三个方向对静风荷载进行分解，采用风轴坐标系时得到横向风荷载FH、竖向风荷载FV以及扭转力矩M。

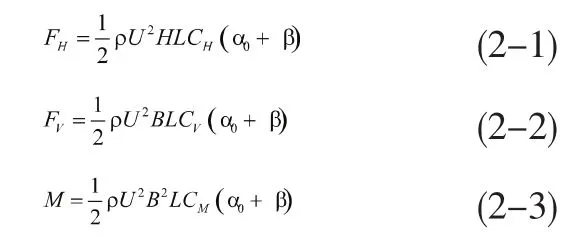
转换到结构整体坐标系下为：

式中：α=α0+β为有效风攻角，α0为初始风攻角，β为主梁扭转变形角；1/2 ρU2为空气平均动压；H，B，L分别为主梁的高度、宽度与长度；CH，CV，CM分别为荷载对应无量纲阻力系数、升力系数及力矩系数。

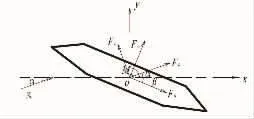
图1 静风荷载示意图

3 非线性静风稳定性分析方法

3.1 非线性静风稳定理论

超大跨度悬索桥为柔性结构，几何非线性效应明显，变形对结构内力平衡方程的影响不能忽略。另一方面，由静风荷载表达式，静风荷载随风攻角改变而变化，在某一静风荷载作用下桥梁结构发生扭转变形，致使风攻角改变，从而反过来又改变静风荷载，因此静风荷载也具有非线性。

非线性静风稳定问题可归结为求解如下形式非线性平衡方程：

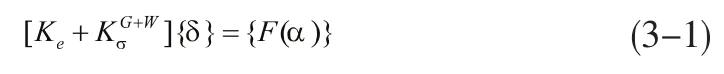
式中，[Ke]、[KσG+W]分别为结构的线弹性和几何刚度矩阵；α为有效攻角；δ为节点位移；F为静风荷载；上标G和W分别为重力和风力。

式(3-1)可写成增量方程组形式：

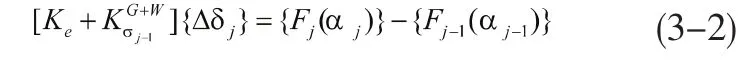
式中， 为第j-1步状态时，由恒载及第i级静风荷载引起的单元内力形成的几何刚度矩阵； 为第j步状态下结构的位移增量列阵； 为第i级风速对应第j步有效风攻角αj的静风荷载列阵。

3.2 分析流程

为有效求解式(3-1)，采用风荷载增量与两重迭代相结合的方法，通过风速分级将风速按一定步长增加，以跟踪结构失稳的全过程，并根据需要适时调整步长以搜索结构的失稳临界风速。在各级风速作用下设置内外双重迭代循环，内层迭代循环计算考虑结构的几何非线性特征后的结构平衡；外层迭代则在某级风速下，根据主梁位移计算结果不断调整静风荷载值，直至风荷载变化不大的平衡位置，由此考虑了静风荷载的非线性影响。

风荷载增量与内外两重迭代法具体求解过程如下：

(1)确定初始风攻角与起始计算风速；

(2)计算该风速条件下的主梁静风荷载；

(3)采用增量法与Newton-Rapson法相结合的方法求解式(3-2)，进行内层迭代，得到结构位移；

(4)检查风荷载及主梁位移是否收敛，如果收敛，则执行步骤 6)；否则，执行步骤(5)；

(5)提取主梁各位置扭转位移，形成新的有效风攻角，重新计算结构的静风荷载，执行步骤(3)～(4)；

(6)按预定步长增加风速，重复步骤(2)～(4)计算；

(7)如果在某一级风速下，外层迭代过程中位移出现发散趋势，或者内层迭代计算中结构位移不收敛，则恢复到上一级风速状态，缩短风速步长，重新计算直至相邻两次风速之差小于预定值为止，最后一级风速为临界风速。

从空气静力失稳的发生机制来看，随着主梁变形增大，一方面结构刚度降低，另一方面风荷载也发生改变，并反过来增大结构变形，结构-荷载不能平衡，最终导致失稳。显然，风荷载迭代不收敛是静力失稳的一个特征，通常被看作空气静力失稳的判据。

4 大跨度悬索桥静风失稳的参数分析

4.1 分析模型概况

以主跨为1 385 m的江阴长江大桥为基础模型分别选择不同的约束体系、主缆矢跨比及主缆安全系数，分析结构参数变化对大跨度悬索桥静风稳定性能的影响，参数取值见表1。

表1 参数取值表

采用ANSYS建立有限模型，加劲梁采用BEAM44单元模拟，桥塔采用BEAM188单元模拟，主缆及吊索采用LINK10单元模拟，采用质量单元MASS21模拟桥面铺装等二期恒载。利用APDL语言编制了通用的悬索桥建模、失稳过程跟踪及临界风速计算程序，只要给定风初始攻角和初始计算风速就可以跟踪结构失稳全过程并得到临界风速。全桥模型如图2所示。

4.2 参数分析结果

（1）约束体系的影响

图3示出了在不同约束体系下的结构静风失稳的临界风速及加劲梁变形。从图中可以看出不同约束体系对临界风速的影响并不大，结构能够承受的最大风速为105 m/s，失稳形式为加劲梁扭转失稳。

图3 不同约束体系的临界风速

（2）矢跨比的影响

图4示出了不同的矢跨比下，结构的静风失稳的临界风速和加劲梁变形情况。从图中可以看出矢跨比对结构静风失稳的临界风速影响较大，矢跨比越小，加劲梁发生扭转失稳及横向挠曲失稳的临界风速越低，而竖向挠曲失稳的临界风速越高。结构失稳的临界风速由加劲梁扭转失稳控制，最大临界风速为104 m/s。

图2 全桥有限元模型

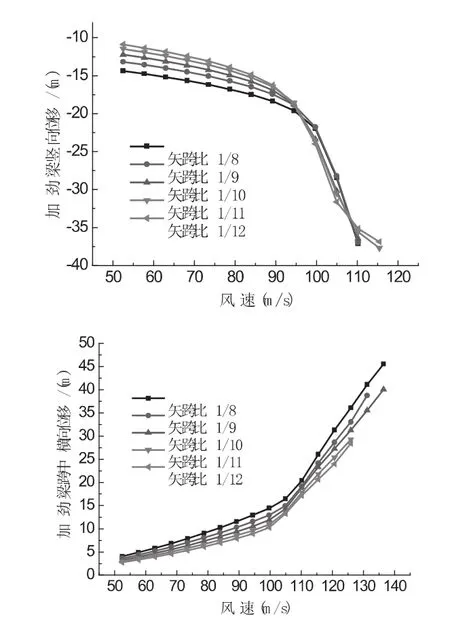
图4 不同矢跨比下的临界风速

（3）主缆安全系数的影响

图5示出了不同的主缆安全系数下，结构的静风失稳的临界风速和加劲梁变形情况。从图中可以看出主缆安全系数对结构静风失稳的临界风速影响较大：主缆安全系数越高，加劲梁发生失稳临界风速越大，结构失稳的临界风速由加劲梁竖向挠曲失稳控制，最大临界风速为94.8 m/s。

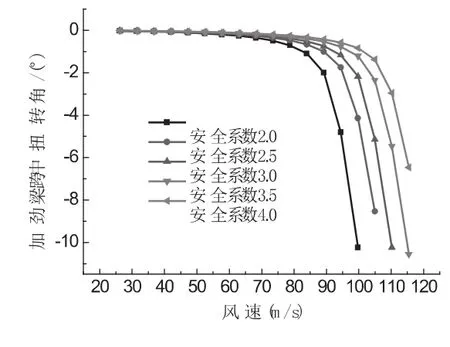
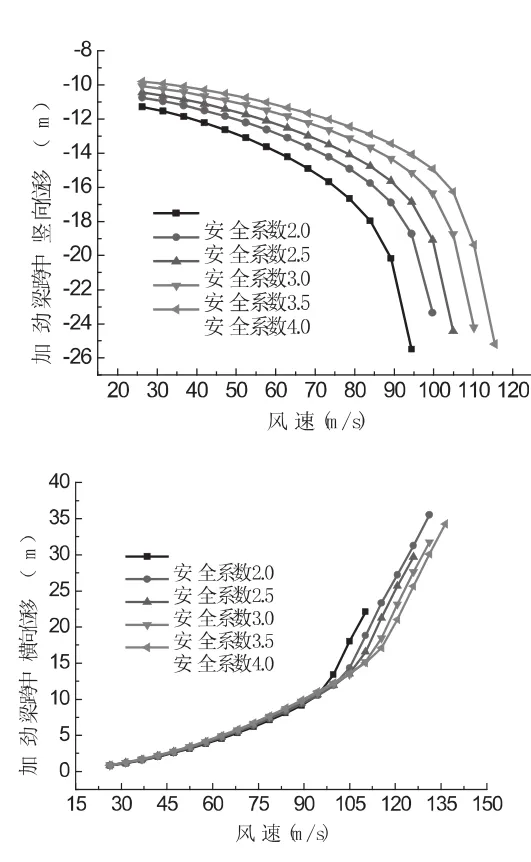
图5 不同主缆安全系数下的临界风速

5 结论

根据悬索桥非线性静风稳定性理论，基于ANSYS软件平台，采用APDL语言编制了大跨度悬索桥非线性静风稳定性分析程序，对影响大跨度悬索桥静风失稳的参数进行了研究，分析结果表明：矢跨比、主缆安全系数是影响大跨度悬索桥静风稳定性的主要因素，加劲梁约束形式对悬索桥静风稳定性影响较小；大跨度悬索桥的失稳往往是由加劲梁的扭转失稳引起，应该采取合理的结构措施增强加劲梁的扭转刚度。