一种基于新型控制器的PMSM矢量控制
浦清云,黄守道
(湖南大学,湖南长沙410082)
0 引 言
电流控制目前常用的有PI控制、滞环控制等控制方案[1-3]。PI控制具有算法简单和可靠性高的特点,因此被广泛应用于工业过程控制中。传统PMSM矢量控制就是个例子。将测得的三相交流电量转化到同步旋转坐标系下,再将PI控制器产生的控制信号转化到静止坐标系下执行,多次坐标旋转变换增加了控制算法实现的难度,且常规的PI控制对正弦的参考电流难以达到理想的控制效果[4-5]。同时,为实现解耦控制,获得良好的动态性能,控制系统中需引入与温度和电路参数有关的交叉耦合项和前馈补偿项,影响了控制系统的鲁棒性;而PR控制器具有能够在静止坐标系下对交流信号进行无静差调节、无需坐标旋转变换、不存在耦合项和前馈补偿项,易于实现低次谐波补偿的优势,但其存在高增益频带过窄的缺点[6],这将导致系统对输入信号频率参量过度敏感,在实际系统中易引起系统的波动。针对上述问题,本文设计了一种基于改进PR控制器的转子磁链定向矢量控制策略,减小了控制算法实现难度,提高了控制系统的鲁棒性和稳定性。
1 改进PR控制器
PR(proportional resonant)控制器是由比例环节和广义积分(GI)环节组成。其传递函数:
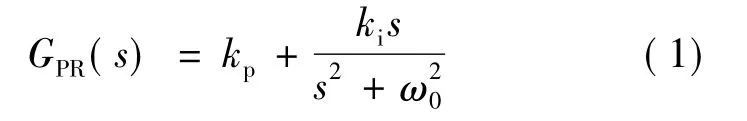
式中:kp、ki分别为比例常数和积分时间常数;ω0为谐振频率。
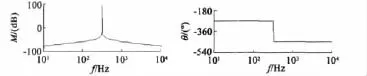
图1 ω0=100πrad/s时的波特图

式中:ωc为截止频率。
从图2可以看到,改进的G'(s)不改变在频率点ω0处为高增益的特性,且高频增益频带加大,ωc越大,其高频增益频带越宽。因此可以将改进的G'(s)应用到PR控制器中,得到其改进的PR模型。

图2 ω0=100π rad/s,ωc=2 rad/s及ω0=100 π rad/s,ωc=10 rad/s的波特图
为了便于实现改进的PR控制器在数字系统中的离散化,将式(2)中改进的广义积分项分解为三个简单环节,令:

式(3)等效于:
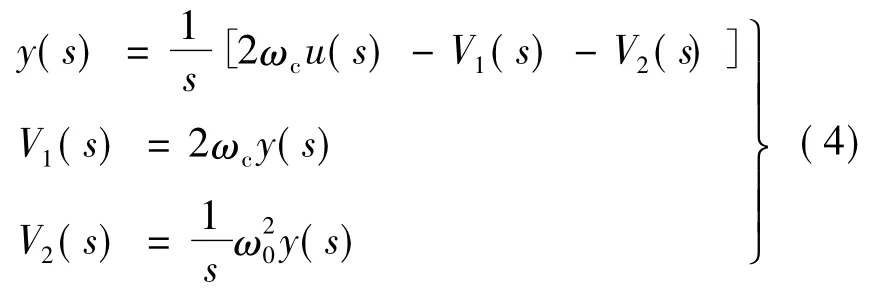
根据式(4)得到相应的原理框图如图3所示。可以看出将其分解后更为明了且容易实现。
将其离散化得:
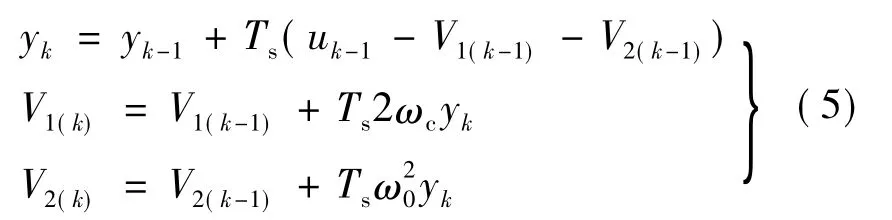
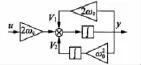
图3 改进广义积分原理框图

将其离散化得:
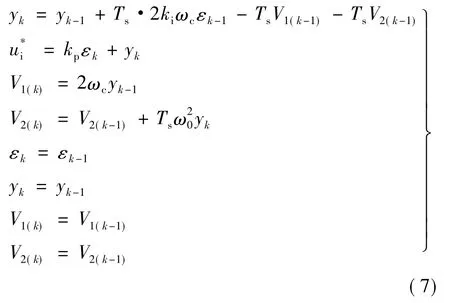
2 PMSM矢量控制
2.1 PMSM 数学模型
根据PMSM控制理论[7],忽略参数变化、磁滞、涡流损耗、转子无阻尼绕组等,基于旋转坐标系d,q轴的PMSM定子磁链方程:
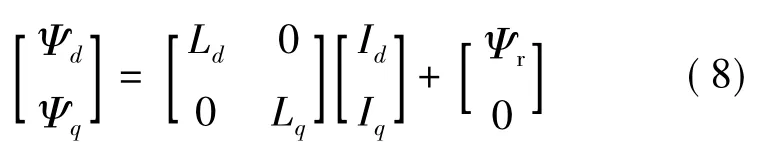
式中:Ψr为转子磁链在定子上的耦合磁链;Ld、Lq分别为PMSM的d、q轴电感;Id、Iq分别为定子电流矢量的d、q轴电流。
PMSM在d、q轴上的定子电压方程式:

式中:Vd、Vq分别为定子电压矢量V的d、q轴分量;ωr为转子旋转角速度。
在认为旋转坐标系的旋转角频率与转子旋转角频率一致,且当d轴与转子主磁通方向一致时,将式(8)代入式(9)得到PMSM转子磁通定向的电压回路方程式:
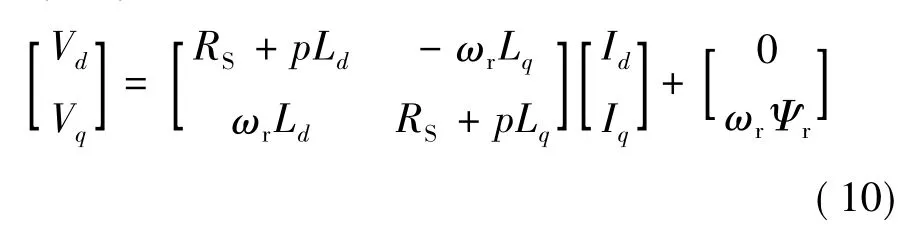
电磁转矩方程:

式中:p为电机极对数。
基速以下恒转矩运行区中,采用转子磁链定向的PMSM定子电流矢量位于q轴,无d轴分量,即Iq=I,Id=0,定子电流全部用来产生转矩。而对于面贴式永磁电机而言,气隙均匀,即Ld=Lq,因此PMSM的电压方程可写:
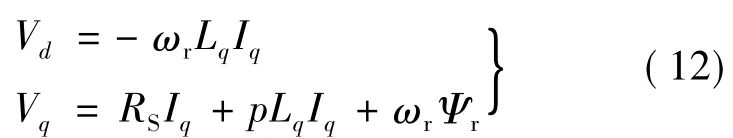
电磁转矩方程可简化:

由上述可知,基速以下,定子电流给定时,控制Id=0可更有效产生转矩,由式(13)可知,控制Iq就能控制转速实现矢量控制。
2.2 基于PR下的PMSM控制策略
基于以上分析,结合传统方法,可将系统设计为基于PI控制器及转子磁链定向的矢量控制系统。其系统控制原理如图4所示。
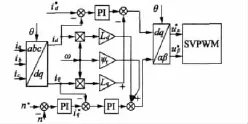
图4 基于PI的PMSM矢量控制策略
图4中,进行d、q轴电流的解耦,电流反馈和电流PI调节器构成双闭环。为提高系统的抗扰动能力,通常需引入电流状态反馈和电网电压作为前馈补偿。图5为基于改进PR的PMSM矢量控制策略。对比发现,它无需耦合项ωLiq、ωLid和前馈补偿项ωΨr,消除了电路参数对系统控制的影响,提高了系统鲁棒性。
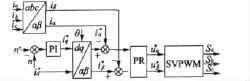
图5 基于改进PR的PMSM矢量控制策略
3 结果与分析
依据上述数学模型和控制策略,利用Matlab/Simulink仿真工具,对基于改进PR控制器的PMSM进行了转子磁链定向矢量控制仿真研究。PMSM参数如下:额定电压UN=380 V,定子电阻Rs=0.86Ω,定子电感Ld=Lq=11.3 mH,电机极对数p=4,转子磁链 Ψr=0.25 Wb。转速给定n*=2 500 r/min,t=0.13 s时转速给定突变为n*=3 000 r/min。负载方面,在t=0.11 s时,突加TL=7 N·m;t=0.12 s时除去负载;t=0.15 s时又突加负载TL=7 N·m。
从图6可以看到,采用PI及改进的PR控制器均能获得良好的动静态转速响应。由图7可以看到,PI控制下在转速给定突变时定子三相电流有一定的脉动,而改进PR控制下无此情况发生。从图8和图9对比可知,在起动、转速给定突变、负载突变时电磁转矩几乎无脉动。图10是经改进PR控制器后静止坐标系下定子电流分量的响应情况。可以看到,其波形几乎重合,可以说明在改进PR控制器下交流电流跟踪得非常好,误差非常小,验证了改进PR控制器应用于PMSM矢量控制中的优势。
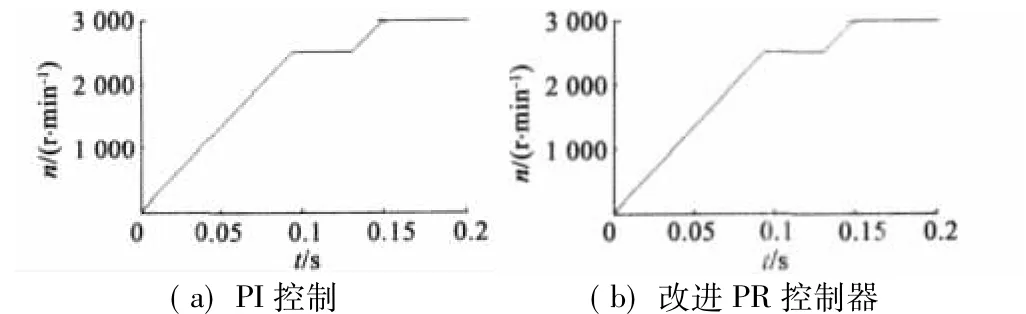
图6 PMSM转速

图7 PMSM定子电流

图8 PI控制下的PMSM电磁转矩

图9 改进PR控制下的PMSM电磁转矩

图10 改进PR控制下定子实际电流与反馈电流
4 结 语
基于PR控制器对交流量能实现无静控制的优点,对其进行优化改进,并将改进的PR控制器应用于转子磁链定向的PMSM矢量控制中,并且通过仿真验证了该方法的可行性。仿真结果表明系统具有良好的动态性能和稳态性能。
[1]赵为,余世杰,沈玉梁,等.光伏并网发电系统的控制方法[J].电工技术,2002(3):12-13.
[2]戴朝波,林海雪.电压源型逆变器三角载波电流控制新方法[J].中国电机工程学报,2002,22(2):99-102.
[3]姜俊峰,刘会金,陈允平,等.有源滤波器的电压空间矢量双滞环。电流控制新方法[J].中国电机工程学报,2004,24(10):82-86.
[4]唐欣,罗安,涂春鸣.基于递推积分PI的混合型有源电力滤波器电流控制[J].中国电机工程学报,2003,23(10):38-41.
[5]孙强,程明,周鹗,等.新型双凸极永磁电机调速系统的变参数Pl控制[J].中国电机工程学报,2003,23(6):117-122.
[6]Teodorescu R,Blaabjerg F,Borup U,et al.A New Control Structure for Grid-Connected LCL PV Inverters with Zero Steady-State Error and Selective Harmonic Compensation[J].IEEE Trans.on Power Electronics Conference and Exposition,2004(1):580-586.
[7]唐任远.现代永磁电机理论与设计[M].北京:机械工业出版社,1997:244-252.

