基于损伤梁桥在控制荷载作用下的有限元分析

王刚 赵扬 赵士辉

0 引言

当前，我国桥梁建设已趋于饱和，已建或建成后不久的桥梁均出现了不同病害。其中，由于当时设计荷载不足，加之日后交通量增大、超载现象频频发生，许多桥梁在建成后不久引起不同程度、不同位置的受力裂缝较为常见。结合桥梁出现的类似病害，考虑相关的研究结论与理论尚较少，给养护部门带来不便。针对此问题，为了更好的给其养护部门提供相应的技术参数及处理意见，对这方面的研究显得非常有必要。

1 实桥简介

洮儿河二号桥(旧)位于洮北区207省道K121+501处，桥梁全长为243 m，桥跨结构(孔数×跨径):13 m×17 m。上部结构每孔采用5片工字梁，采用预制吊装施工，梁高100cm，间距160cm，混凝土标号25号。下部结构采用钻孔灌注桩基础，双柱式墩台，柱顶设置钢筋混凝土帽梁。支座采用钢铰支座。桥面横向布置为 0.5 m(栏杆)+7.0 m(行车道)+0.5 m(栏杆)，总宽8 m，桥面铺装采用沥青混凝土。该桥设计荷载:汽—15、挂—80，建成时间为1982年，主要病害是1/4L，1/2L有受力裂缝，3号～4号主梁之间微弯板处有纵向裂缝，在桥下底部观测时发现行车作用下主梁变形过大。主梁截面及全桥截面尺寸如图1，图2所示。

图1 计算截面尺寸（单位:cm）

图2 主梁截面尺寸（单位:cm）

2 桥梁理论承载能力的计算

本研究只考虑桥梁在损伤后控制荷载作用下的有限元分析，故实际加载均使用老规范荷载。模拟过程如下:按照梁格理论，采用midas.civil进行模拟，共划分157个梁单元。端横隔按实际模拟，厚度h=0.2 m;纵向梁格以1 m为一个单元，跨中部分因无横隔梁，故采用虚拟横梁，横梁梁格截面特性按板厚h=0.2 m，宽b=0.5 m取，间距1 m。支座边界条件设置为简支，主梁节点与支座节点设置梁端释放约束(主梁节点与支座节点之间采用刚性连接)。桥面设置两个车道，车道系数取1，挂车加载按一车道设置［1］，按汽—15，挂—80加载，承载能力按组合荷载计算。最后计算得到在挂车荷载综合作用下42号单元J端，即1号梁跨中内力为最大2018.97 kN·m，从而确定挂—80为该桥控制荷载。然后根据最大内力影响线加载方法找出最不利的移动荷载位置。

3 桥梁实体模型

3.1 实体单元及控制荷载的模拟

整个模拟利用大型有限元软件midas.fea进行，生成实体单元后共2213个单元，边界条件为铰支。其中，Ⅰ型主梁从左至右编号依次定义为1号～5号，Ⅰ型主梁与微弯板按固结处理，Ⅰ型主梁与微弯板组合横截面生成平面单元，划分50个网格单元，然后将该平面单元沿跨径方向按支座长度、损伤位置等进行划分均匀后生成空间实体单元，端横隔板横截面按在Ⅰ型主梁的实际坐标位置与主梁节点共用，将两边主梁节点连成三维曲线，生成平面单元后扩展成实体单元。因midas.fea移动荷载的施加较为不便，故模拟时利用midas.civil移动荷载追踪器找出位置后，控制荷载用等效节点载荷代换来完成。模型如图3所示。

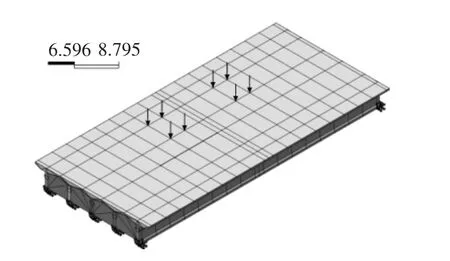
图3 实体单元模型

3.2 损伤的模拟

因各主梁底部1/2L，1/4L处已有受力裂缝并出现损伤，为了方便的找出1/2L，1/4L处的破损位置，在建模时，主梁单元沿纵向尺寸为(0.2+8@1+2@0.3+8@1+0.2)m，(其中，0.2 m 为支座沿跨径方向的长度)。参照有关培训资料，考虑模拟条件的局限性，本文将梁底相应位置处节点分割，以期实现主梁横向裂缝(1/4L，1/2L处损伤位置)、3号～4号梁微弯板间的纵向裂缝。

4 分析

4.1 各根主梁沿跨径方向的主应力分析

将控制荷载作用下，损伤桥梁与未损伤桥梁模型计算所得到的数据整理成图。以下为计算后经提取并整理好的未损伤与损伤桥梁每根主梁的主应力对比分析，如图4所示。

图4 损伤与无损伤情况下桥梁各主梁的主应力对比分析

从数据及图形分析能够得到如下结论:1)将1/2L，1/4L跨做损伤与未损伤模拟，每根主梁主应力在跨径方向上的分布趋势相同。各根主梁主应力在跨中位置，有损伤的要大于无损伤的，其中，1号主梁在桥跨1/2处有损伤位置承受的拉应力较大，而且有突变现象，较明显，有此明显现象主要是因行车控制荷载作用下在此处产生最大内力、裂缝位置有应力集中现象造成的。2)各根主梁主应力在支座位置及1/4L跨之间，有损伤与无损伤的情况相比，有损伤主梁承受的主应力与无损伤主梁位置承受的应力相差不大，在1/4L位置，损伤桥应力要小于未损伤桥应力。

4.2 损伤后在控制荷载作用下各主梁跨中裂缝宽度及相应挠度

4.2.1 损伤后在控制荷载作用下各主梁的跨中裂缝宽度

本次研究假设该桥材料为线弹性结构计算，故裂缝宽度的数值也为线弹性材料在荷载作用下的裂缝宽度。经过控制荷载的实际作用，通过midas.fea软件实际分析得到各根主梁在行车荷载作用下的最大宽度，以供养护参考，数据整理如表1所示。

表1 各主梁跨中裂缝最大宽度 mm

结合《公路桥梁养护技术规范》［2］承重结构在车载作用下跨中裂缝最大不允许超过0.5mm，可知在挂车控制载荷作用下，位于挂车车道附近的1号，2号，3号主梁均裂缝超限，说明主梁刚度将有所下降，4号，5号缝宽未超限。但因上述车载的布置只是为了得到该桥内力的控制荷载而考虑，人为的将车道定于左幅。而实际行驶中挂车行驶在右幅，所以在控制荷载作用下，该桥各根主梁跨中裂缝均超限。即说明在损伤情况下，理论的控制荷载作用将对该桥裂缝破损有加剧破坏的趋势。

4.2.2 损伤后在控制荷载作用下各主梁的跨中最大挠度

经过控制荷载的实际作用，通过midas.fea软件实际分析得到各根主梁在行车荷载作用下的最大挠度，以供养护参考，数据整理如表2所示。

表2 各主梁跨中最大挠度 cm

参照预应力混凝土桥涵设计规范，主梁的最大挠度不应超过计算跨径的L/600，可知1号，2号梁在跨中损伤时控制荷载作用下最大挠度将超过规范允许值，3号梁因处于行车道中间，在损伤后挠度未超过规范数值，同理，如挂车作用右车道位置，4号，5号梁跨中挠度也将超过规范允许数值。即说明只要在损伤情况下，理论的控制荷载作用将对该桥刚度有明显影响，如果未加固的情况下，在超限荷载作用下对该桥的抗弯性能将会有更大的折损。

综上分析，若桥梁因超载或其他原因发生如上损伤，即便是在理论的控制荷载作用下，对该桥的破坏也是十分明显的。因此若从长远角度考虑，为使桥梁结构不受损坏，设计部门一定要尽量提高桥梁的设计等级，此外路政部门加大超载车辆的控制、处罚力度，也是使桥梁不受损害的重要手段。

4.3 微弯板有纵向裂缝下的横、竖向剪应力研究

为了更好的研究微弯板有裂缝作用下的剪应力分布，本次特意选取裂缝长度方向的端部、中部、尾部，不利车载作用的所有位置及无裂缝状态下的位置查看应力，将裂缝长度方向的横向、竖向剪应力数据提取整理，如图5所示。

图5 纵缝方向对应的横竖向剪应力

经研究数据得到如下规律:在纵向裂缝损伤情况下，沿裂缝长度范围内，靠近车后轮载荷的裂缝横向剪应力最大，相对车前轮载荷的裂缝横向剪应力相对略小，而裂缝的两端部横向剪应力相等(不是最大)，基本呈波浪形式。竖向剪应力明显要大于同一位置的横向剪应力，距车载较远的端部出现最大负剪应力，是对应的横向剪应力的近40倍，其他位置相对降低，在接近裂缝长度1/3位置出现最大正剪应力。

结合数据分析得到如下结论，在控制荷载作用下及微弯板有纵向裂缝情况下，产生的横竖剪应力因数值较小，对整个桥面不构成加剧损伤破坏的影响。

5 结语

1)通过损伤与未损伤梁桥模拟分析，得出了两种工况下各主梁沿跨径方向的主应力分布趋势、损伤与未损伤位置主应力谁大谁小的结论。

2)该桥在设计控制荷载不超限的情况下行驶，如跨中有损伤，跨中挠度、裂缝宽度均将超过规范允许范围，有加剧破损的影响。

3)得出了桥面微弯板有纵向裂缝情况下的横向、竖向剪应力分布规律，通过计算数据证明在控制荷载作用下该剪应力对其不构成加剧损伤的影响。

［1］ JTG D260-2004，公路桥涵设计通用规范［S］.

［2］ JTG H11-2004，公路桥涵养护技术规范［S］.

［3］ 张 鑫，江光炫.某反修桥加固设计加固原理［J］.山西建筑，2010，36(9):332-333.