射频自适应干扰抵消系统的分析与设计

邹 敏,纪学军

(中国电子科技集团公司第五十四研究所,河北石家庄050081)

0 引言

在现代武器装备中,同一个平台上往往存在大量的接收和发射设备,特别是在电子对抗设备中经常存在大功率干扰与高灵敏度的接收设备,为了使得所有设备能正常工作,传统的做法就是通过复杂的频谱管理使设备分时分频工作。但是在信息密度极高的现代战争环境下,战场形势瞬息万变,重要设备的分时工作意味着可能丢掉重要战场情报,这将使得设备的战术性能大大降低,还可能造成重大损失。自适应干扰抵消系统则是解决这个问题的一种有效手段,自适应干扰抵消不仅能使得同平台的接收和发射设备同时工作,而且还可能同频工作。这样在提高装备战术性能的同时,还提高了频谱利用率,减轻了复杂电磁环境下的频谱管理难度。

在基于最小均方(LMS)算法的自适应干扰抵消系统原理的基础上,重点对系统的射频实现方式进行了分析,给出了具有较强工程指导意义的设计公式,对工程设计中的一些问题进行了讨论,并给出了解决方法。

1 系统模型

自适应干扰抵消系统原理如图1所示。图1中vm(t)为从天线接收的干扰信号;vr(t)为与干扰信号相关的参考信号,一般由本地接收机从发射机取样得到;w(t)为对参考信号vr(t)的加权值;e(t)为抵消后输出的误差信号。参考信号vr(t)经过w(t)加权调整以后与干扰信号vm(t)求和,求和误差e(t)作为抵消后的输出信号。为了适应干扰信号vm(t)幅度和相位的变化,w(t)将随vm(t)的变化进行自适应的调整。调整过程由最优化算法实现如LMS算法,自适应调整的结果使得误差信号e(t)达到最优化算法收敛的极小值。

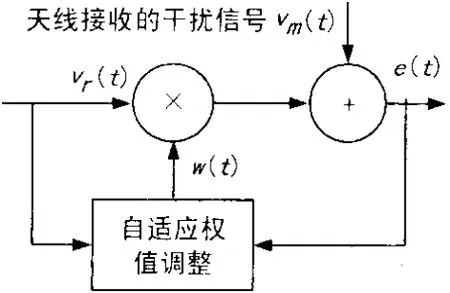
图1 自适应干扰抵消系统原理模型

定义干扰信号vm(t)与误差信号e(t)的功率比为自适应干扰抵消系统的抵消比(ICR),ICR将作为衡量系统性能的主要指标。

设本地发射机辐射的信号为:

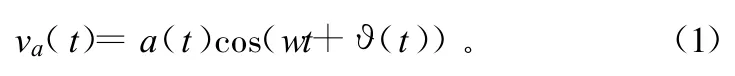
式中,a(t)、θ(t)分别为信号幅度和相位。由本地接收机接收的干扰信号为:

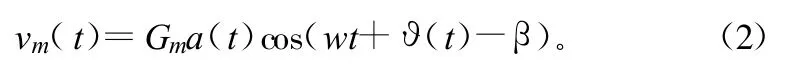
式中,Gm、β分别为信号由发射天线传播到接收天线的幅度衰减和相移。本地从发射机取样的干扰信号为:

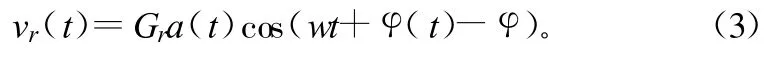
式中,Gr、φ分别为取样系数和相移。对于以LMS算法进行自适应调整的抵消系统的抵消比可表示为:

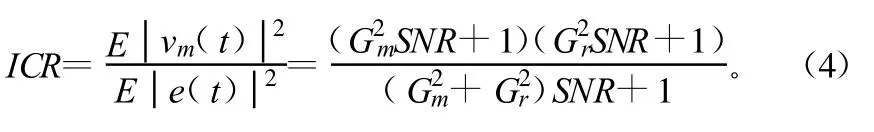
式中,SNR=pa/pn,pa为发射信号功率,pn为系统随机热噪声。这里得到的抵消比没有考虑系统实现方式,忽略了系统本身误差,是系统理想情况下具有的性能。对于具体的抵消系统,抵消比则必须考虑系统引入的误差,抵消比将在式(4)的基础上进行修正,并且主要由系统本身参数来描述。

2 射频实现方案的设计与分析

在实际应用中,为了保护接收信道,通常大信号干扰抵消需要在射频最前端完成,这样一来,系统直接在射频段实现就变得很有必要。现有资料已指出,射频实现LMS算法比较适合自适应干扰抵消系统,特别是在微波频段。

这里基于正交矢量合成原理对自适应抵消系统的射频实现方案进行设计和分析。方案原理框图如图2所示。

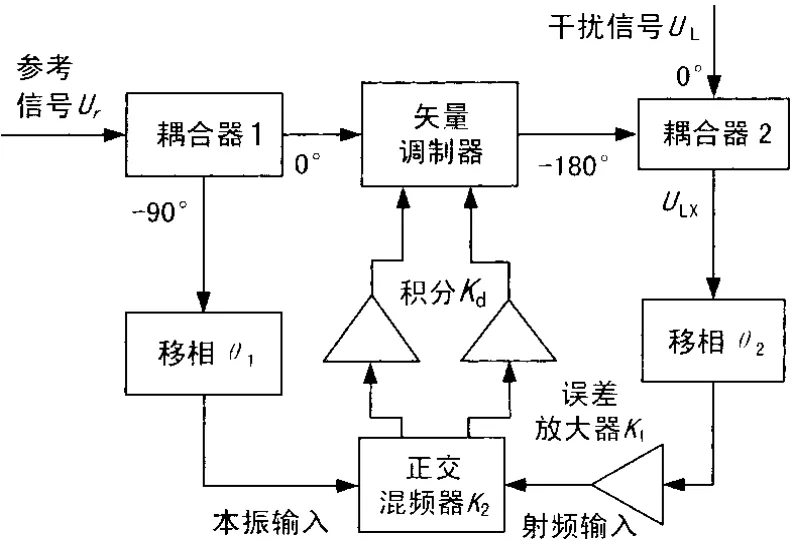
图2 系统的射频实现方案

UL为到达的干扰信号,其相位为 ϑL,ULx为耦合器2输出端抵消后剩余的误差信号,其相位为ϑLx,取样的参考信号为Ur,其相位为 ϑr。Ur与ULx的相位差为ϑ=ϑLx-ϑr,耦合器1到混频器本振端的路径相移为ϑ1,耦合器2到混频器射频输入端的路径相移为 ϑ2,耦合器1到矢量调整器的路径相移为 ϑ3,矢量调制器到耦合器2的路径相移为 ϑ4,其中耦合器1,耦合器2为3 dB耦合器,对于耦合器引入的路径移相,耦合器1为 ϑ5,耦合器2为 ϑ6,正交混频器和矢量调制器的路径移相分别包含在 ϑ1、ϑ2、ϑ3和 ϑ4中,耦合器 1 为 90°混合网络 ,耦合器 2为180°混合网络,环路中以二阶低通滤波器代替理想积分器完成算法的积分功能。误差放大器增益为K1,混频器传输系数为K2,矢量调制器传输系数为K3,滤波器增益为Kd,矢量调制器调制斜率为M。

正交混频器同相输出端积分器输出信号为:

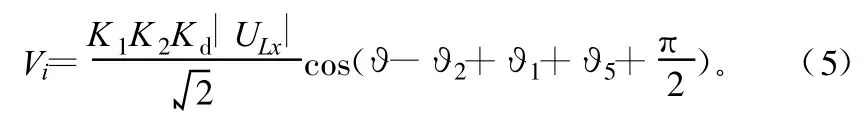
正交混频器反相输出端积分器输出信号为:

矢量调制器输出信号为:

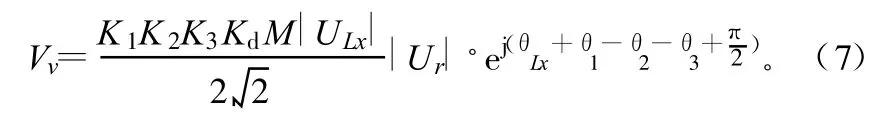
耦合器2输出端输出抵消以后的信号为:

则系统的抵消比ICR可表示为:

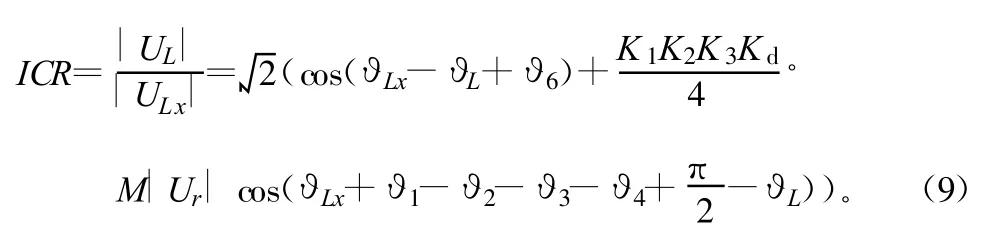
从式(9)中可以看出,系统要达到最佳的抵消效果即达到最大的抵消比需要满足:

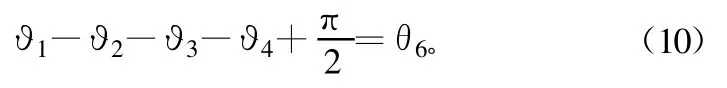
式(10)说明要达到最佳抵消效果,系统中耦合器1直通端口到正交混频器本振端口的电长度应该与耦合端口通过矢量调制器,耦合器2和误差放大器到达正交混频器射频输入端口的电长度相等。

式(9)和式(10)是图2描述的射频自适应干扰抵消系统工程设计的重要依据,特别是系统工作带宽较宽时,能否满足式(10)给出的条件成为系统设计成功的关键。

3 系统测试结果

基于图2描述的方案,设计实现了工作在225～400 MHz的自适应干扰抵消系统。系统实测结果如表1所示。从测试数据可以看出,抵消系统对连续波的平均抵消比接近50 dB,抵消时间小于1 ms。而且系统对于带宽小于2MHz的宽带信号也有不小于30 dB的抵消。

表1 射频自适应干扰抵消系统测试结果

4 问题分析与讨论

用作积分功能的低通滤波器会对抵消误差产生较大影响,在满足抵消时间和系统稳定性的条件下,通过减小电阻、增大电容的方式,可使系统更加接近理想积分器,使得系统抵消误差大大减小,从而增大系统抵消比。

在高抵消比的条件下,需要较大的环路增益,而增大误差放大器增益则是提高环路增益最有效的方法,但是这将在一定程度上影响系统稳定性,造成系统比较容易自激振荡,产生较大的杂散。在高增益的条件下解决系统稳定性的问题,需要做好放大器各级之间及放大器与正交混频器等系统中其他器件的匹配和隔离。也应该选用端口间隔离度足够大的正交混频器,这不仅能够保持系统的稳定性,而且能够使得系统获得较好的线性度,从而减小误差,增大抵消比。对于抵消时间的调整,除了调整环路带宽以外,足够大的本振驱动也能减小抵消时间,加快系统的收敛速度。

5 结束语

上述对于系统模型的分析结论适用于任何实现形式的基于LMS算法的自适应干扰或噪声抵消系统的性能分析,具有广泛的适用性。在此基础上设计完成的射频自适应干扰抵消系统,工作频段宽、抵消比大、抵消速度快,完全满足了收发隔离、同平台多电台同时工作等电磁兼容方面的需要。但是系统对于宽带干扰的抵消性能还有待提高,以适应不断发展的宽带通信的需要,也是目前系统改进的一个重要方向。

[1]顾 杰.空间自适应干扰抑制系统对抗研究[J].电子信息对抗技术,2006,21(2):23-26.

[2]曾茂生.提高电子战系统收发隔离的方法研究[J].舰船电子对抗,2008,32(1):54-55.

[3]田海林,王海平.机载电子干扰机自适应收发隔离技术研究及仿真[J].弹箭与制导学报,2006,26(4):405-407.

[4]刘连柱,金吉学.系统收发隔离解决方法探讨[J].电子对抗,2006,8(3):43-45.

[5]TOBIAS D.An Active Feedback Interference Cancellation Technique for Blocker Filtering in RF Receiver Front-Ends[J].IEEE Journal of Solid-State Circuits,2010,45(5):989-996.

[6]JIANG Yun-hao,ZHAO Zhi-hua.Influence of Different Gainsto AdaptiveInterferenceCancellation System[C].China:Electromagnetic Compatibility(APEMC),2010 Asia-Pacific Symposium on,2010:1394-1397.