基于扩展卡尔曼滤波的水下目标测量系统

李智生,余义德,杜寅峰,李 钊

(1.中国人民解放军91550部队,辽宁大连116023;2.中国人民解放军65547部队,辽宁海城114200;3.第二炮兵驻石家庄地区军事代表室,河北石家庄050002)

0 引言

水下目标运动测量系统用于精确测量目标航迹的大地坐标和目标相对大地的航速。由于目标声纳基阵波动和测量引起的误差,使得测得的目标位置围绕真值上下波动。为此,系统所测得数据仍是一种随机变量,若不对该数据近一步的处理,就无法得到满意的精度[1]。

研究应用扩展卡尔曼滤波方法对测量数据进行精度评估,推导了相应的滤波公式,建立了一种扩展卡尔曼滤波算法。通过系统的仿真结果表明该算法收敛速度和估计精度能够满足系统要求。

1 卡尔曼滤波公式的推导

卡尔曼滤波是以最小均方误差为准则的最优估计,是一种对动态系统进行数据处理的有效方法。用于目标跟踪定位的卡尔曼滤波器通常是一种典型的非线性滤波器,它具有下列矩阵方程[2,3]:

状态方程:

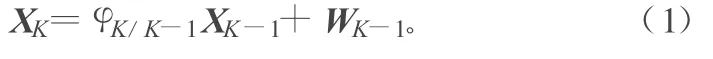
量测方程:

预报估计:

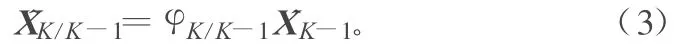
滤波估计:

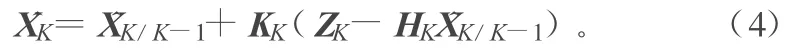
预报误差协方差阵:

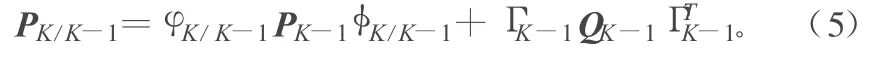
滤波误差协方差阵:

最佳增益矩阵:

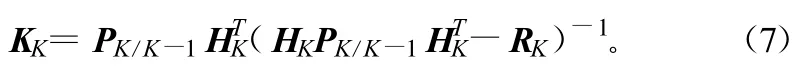
式中,φK/K-1为N×N状态转移矩阵;WK为动态噪声;VK为观测噪声,且WK与VK是互不相关的零均值白噪声序列;ΓK为N×N噪声转移矩阵,即对所有k,j,有EWK=0,EVK=0;ZK为N×1测量向量。

根据上述递推公式之后,如果已知K-1时刻的状态估计 ^XK-1及估计误差的协方差阵 PK-1,就可以根据K时刻的量测值ZK得到K时刻的估计^XK和相应的误差协方差矩阵PK。

2 卡尔曼滤波在系统中的应用

测量系统利用线缆拖曳加载GPS天线的移动通信平台,GPS天线能够实时获取移动通信平台坐标参数,同时移动通信平台上装载的水听器能够实时接收目标发出的声纳信号,通过计算声纳脉冲的时延时间和目标的方位信息,便可实时计算目标相对移动通信平台的相对距离和方位,从而可以准确推算目标的位置。

2.1 系统模型

建立恰当的数学模型是卡尔曼滤波模型的滤波成败的关键。一个好的数学模型既要反映目标的动态特征,又要足够简化,以保证计算简便和速度。这里针对目标的运动状态来建立相应的模型,目标在水下航行过程可基本视为匀速运动,且大体上按某个设定的深度航行。因此,把状态方程和量测方程都设置在直角坐标系中[4]。

在直角坐标系中,可用一个线性动态模型和一个非线性观测模型来建立目标的运动模型。在直角坐标系中,把移动通信平台O和目标都看作质点来处理,则系统的动态模型为:

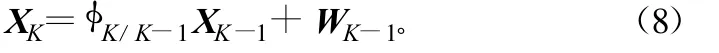
式中,状态向量X=(x,y,z,vx,vy,vz)T为目标相对于移动通信平台O的相对位置;v为相对目标速度。

考虑如下情形:移动通信平台相对静止不动,目标在水下某一平面作匀速直线运动,则在测量时间间隔内,通过移动通信平台O上的被动声纳设备可测得目标与移动通信平台的相对距离俯仰角和方位角的数据序列。设测量时噪声为高斯白噪声,因为移动通信平台静止,所以此时v为目标的绝对速度,其中vz为0,于是目标的状态向量为X=(x,y,z,vx,vy)T。

目标在tK时刻的位置可以表示为:

式中,C为未知参数。则目标的状态方程为:

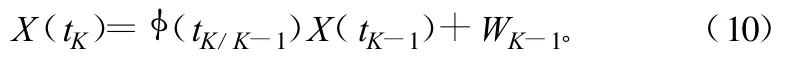
转移矩阵为:

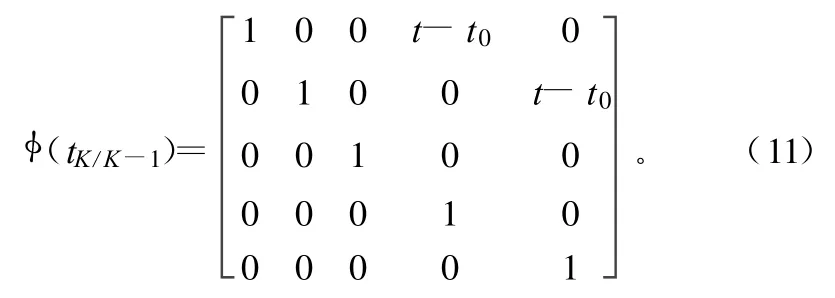
目标与移动通信平台之间距离的量测方程为:

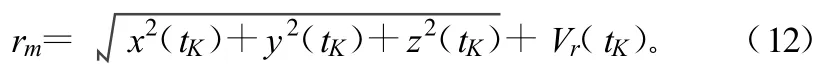
该距离是利用声纳脉冲的时延值计算得到的。

目标的俯仰角测量方程为:

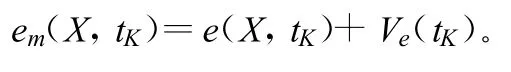
目标的方位角测量方程为:

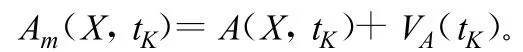
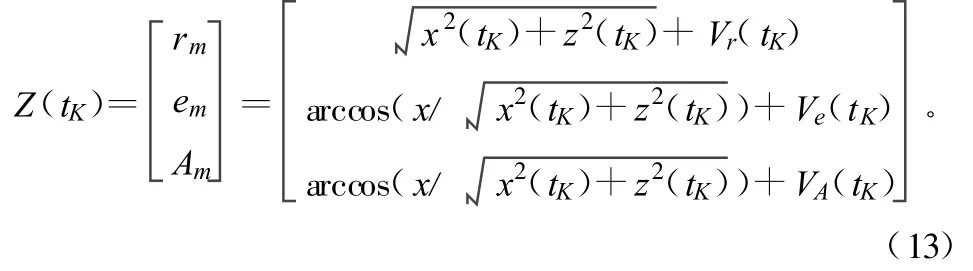
写成向量形式为:

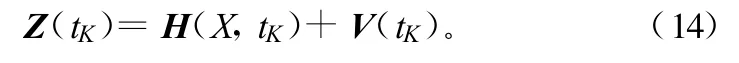
将量测方程中的观测矩阵H(tK)线性化,需要求其雅可比矩阵,即

至此,得出了目标的状态式(10)和量测方程式(14),根据式(3)～式(7),给出恰当的X(0/0)和P(0/0),以及测量误差方差,即可在线、实时地计算下去,并不断地得到目标运动要素的最小方差估计及估计误差方差。

2.2 滤波初值的设定

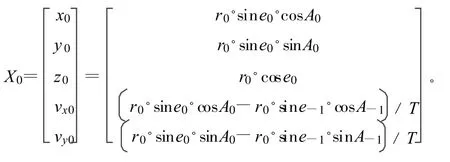
式中,T为信号周期,在本系统中,T=0.1 s,而误差协方差阵的定义为:

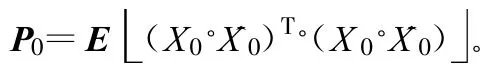
则状态估值初始协方差阵为:

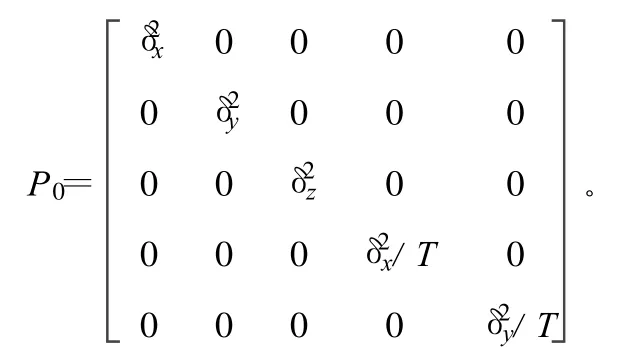
3 实例仿真

以移动通信平台为坐标参考点,在水深30 m处,水下航行器距离移动通信平台60 m处匀速直航靠近移动通信平台,航速为4 m/s,水下航行器相对移动通信平台的初始方位为45°,状态更新频率为0.1 Hz。假设测量噪声符合零均值、方差 δ2=3的高斯分布,则目标的初始状态为:X0=(21.21,21.21,51.96,1.4,1.4)。

利用r0,e0,A0的数据加噪声干扰,作为测量值,根据测量值,用本文的卡尔曼滤波方法计算所有时刻X=(x,y,z,vx,vy)T的估计值。目标真实航迹和经卡尔曼滤波后的估计轨迹,其中虚线表示滤波后的估计轨迹如图1所示。x方向位置的估计误差如图2所示。航速的轨迹误差如图3所示。从图1可知:滤波算法在第60个滤波周期开始收敛,且比较平稳。图2可以看出,整个航程内,x方向误差都在10 m以内,符合系统设计要求。由图3可知,航速估计在第10个周期内开始收敛,且误差在1 m内,能够满足系统要求。

图1 目标真实航迹和经卡尔曼滤波后的估计轨迹

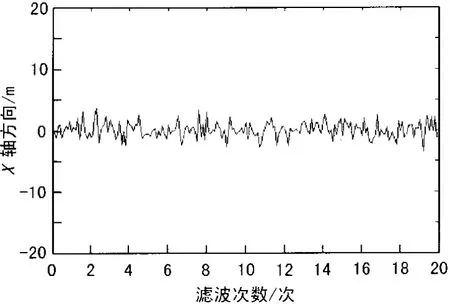
图2 x方向位置的估计误差

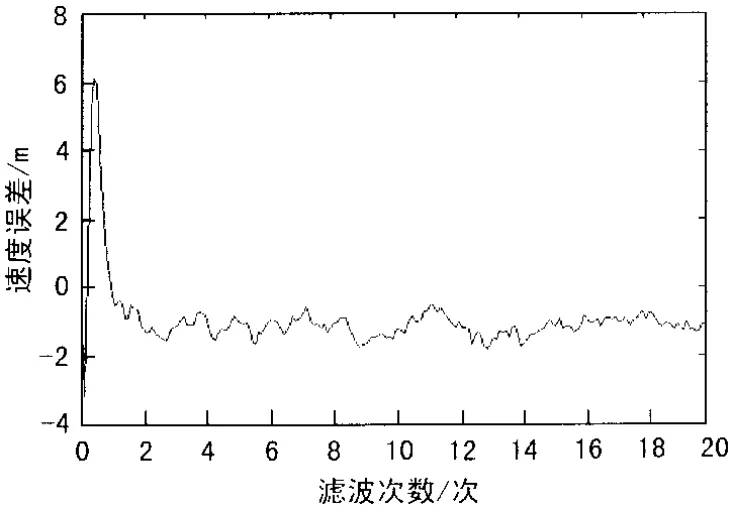
图3 航速的轨迹误差

4 结束语

对基于扩展卡尔曼滤波的水下目标航迹测量系统的滤波算法进行研究,建立了水下目标运动状态方程和测量方程,针对非线性测量方程,采用雅克比矩阵进行了线性化处理。仿真结果表明,该滤波算法有较快的收敛性和较好的估计精度,能够满足系统要求。该方法也可以扩展应用到其他工程领域。

[1]AIDALA V J.Kalman Filter Behavior in Bearings-only Tracking Applications[J].IEEE trans.Aerospace and Engineering Systems,1979,15(1):29-39.

[2]SONG T L,SPEYER J L.A Stochastic Analysis of a Modified Gain Extended Kalman Filter with Application to Estimation with Bearings-only Measurements[J].IEEE Trans.Automatic Control,1985,30(10):940-949.

[3]周 丰.基于卡尔曼滤波水下弹道测量系统研究[J].弹道学报,2004,16(3):66-69.

[4]刘 伟,王昌明,赵 辉.基于卡尔曼滤波水下近距目标运动分析[J].弹道学报,2008,20(4):28-31.