一种改进的GNSS多径抑制性能评估方法

张志新,蔚保国,邢兆栋

(河北省卫星导航技术与装备工程技术研究中心,河北石家庄050081)

0 引言

多径已经成为影响全球卫星导航定位系统(Global Navigation Satellite System,GNSS)精度的主要误差源,如何抑制多径成为研究热点。现在评估多径性能的方法主要是多径误差包络曲线[1]。

目前研究广泛的多径误差包络曲线是基于一种简单化的多径模型得来的。这种简单化多径模型是采用和接收信号相同的信号表达形式,与期望接收的卫星导航信号不同的地方是多径的衰落幅度、到达接收机的时间,在研究时,多径信号的幅度选择小于期待接收的卫星导航信号,到达时间长于所期待接收的信号。该模型下的多径误差包络曲线描述的是理想情况下存在一条几何多径所造成的接收机多径误差。该多径误差包络曲线可以分析不同调制方式信号的多径性能,但由于多径模型与环境因素无关,因此不能反映实际环境中多径信号的特性和多径对接收机产生的真实影响。

1 多径信号模型分析

在分析信号的抗多径性能时,使用的多径信号模型是非常简单化的多径模型。在理论研究中,一般采用的多径模型是和接收的卫星导航信号特征是相同的,唯一不同之处是信号衰减幅度和传播时间延迟。这种多径信号模型并未考虑到多径信号与环境的关系。

多径和环境是密切相关的,不同环境下的多径是不相同的,因为环境具有复杂性,因此多径也是很复杂的,根据学者的多年研究,得出多径信号具有随机信号的特点[2]。在路地移动服务 LMS(Land Mobile Satellite Services)信道模型[3]中,将卫星信号分为直视信号(Ligh of Sign,LOS)、近反射多径信号和远反射多径信号3种,而3种信号的分布特性各不相同。LOS信号的幅度分布在有阴影存在的情况下服从Rice分布或Rayleigh分布。近反射多径信号和远反射多径信号的数目服从Poisson分布,幅度服从Rayleigh分布。近反射多径信号的时间延迟服从指数分布:

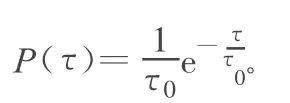
式中,τ0为不同环境下的典型时间延迟,远反射信号时间延迟服从均匀分布。

此模型具有随机特性,能够反映不同环境下的多径信号的随机特性。

以上多径模型是和实际环境最贴切的模型,也是最复杂的模型,分析其多径特性需要考虑到环境的因素,因此分析也比较复杂,因此为了便于分析,研究一种相对于随机信道模型的简化随机信道多径模型。

假定多径信号功率为P*(τ),其分布[4]为:

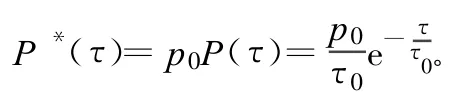
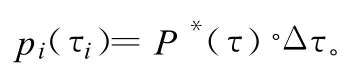
相对应多径信号幅度为:

2 多径误差包络曲线

环境相关的多径误差包络曲线根据以上2种多径模型可以分为复杂多径模型的多径误差包络曲线(对应于随机信道多径模型)、简单多径模型的多径误差包络曲线(对应简化随机信道多径模型)2种。这2种多径模型的多径误差包络曲线反映出多径与环境的关系,在分析不同调制方式信号的多径性能和多径抑制技术方面具有更好的指导意义。

复杂多径模型多径误差包络曲线是基于随机信道多径模型提出的。根据多径的随机性特点,其延迟分布是P1(τ),幅度分布是P2(τ),即

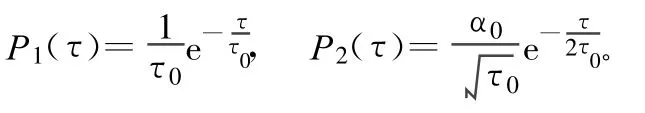
式中,α0为反射因子。联合以上分布可以得到多径信号的时延与幅度的联合分布:

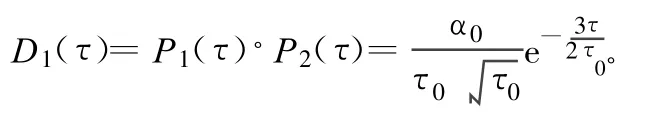
从而得到复杂多径模型多径误差包络曲线:

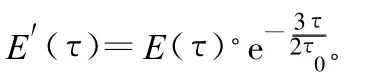
式中,E(τ)为常用的非常简化多径模型的多径误差包络曲线函数,其反映的是理想情况下的简化多径模型的多径性能。

简单多径模型多径误差包络曲线是基于简化随机信道模型的评估方法。假设α0对应于SMR(信号和多径幅度之比),则多径信号的时间延迟和幅度的联合分布为:

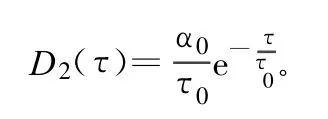
因此简单多径模型的多径误差包络为:

3 仿真比较分析

以GPS C/A码为例,地理环境选择为开阔地区、乡村、郊区和城市市区4种不同的环境,4种不同环境下典型的多径参数[7]为:在接收机仰角为25°时,开阔地区的 SMR(Signal-Multipath Ratio)为27.5 dB,典型时间延迟为26 m,乡村环境的SMR为13.5 dB,典型时间延迟为 57 m,郊区的SMR为20.5 dB,典型时间延迟为56 m,城市市区的SMR为6 dB,典型时间延迟为51 m。在4种环境下进行仿真(仿真参数设定相关器间隔d=0.1 chip),得到2种多径误差包络曲线[6]如图1和图2所示。

图1 多径误差包络曲线

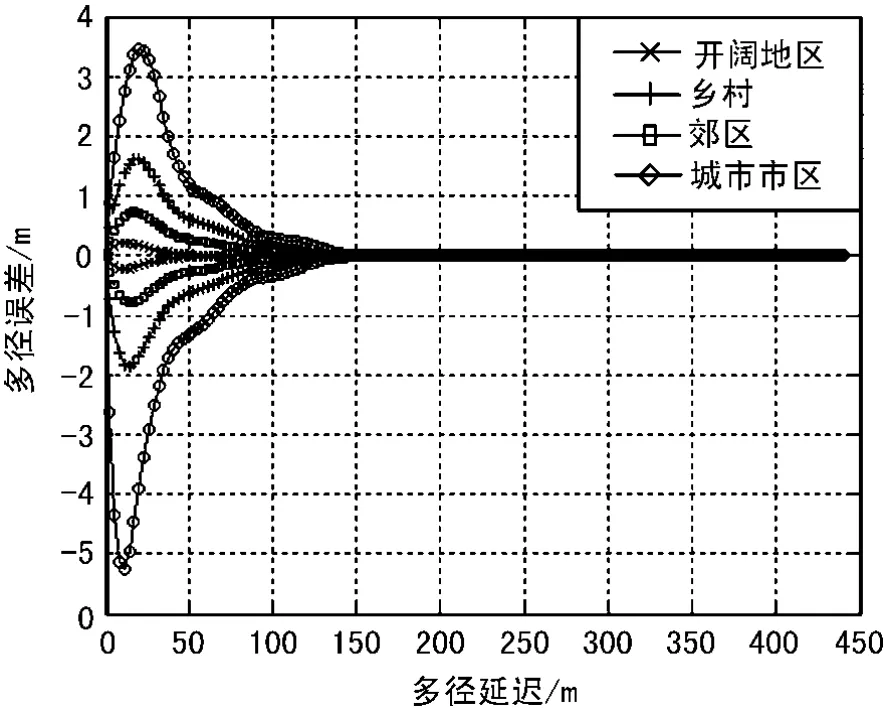
图2 复杂多径模型多径误差包络曲线

从图1和图2可以看出,GPS C/A码的多径抑制性能在多径误差包络曲线和复杂多径模型多径误差包络曲线2种评估情况下,存在很大的不同。4种环境下比较图1和图2,图2的多径误差包络的最大值均比图1多径误差包络的最大值小;多径对信号影响的持续时间,图2持续的时间比图1中多径影响持续时间短;在包络面积方面直观可见,图1的任何环境下的包络面积都比图2同样环境下的包络面积大的多,通过计算可以得出:图1中开阔地区、乡村、郊区、城市市区环境下分别可以抑制多径75%、75.5%、75.3%、76%,图2中4种环境下分别抑制多径85.5%、84.8%、84.9%、85.1%。

同样以GPS C/A码为例,在开阔地区、郊区、乡村、城市4种环境下进行仿真,仿真条件设定为相关器间隔d=0.1 chip,仿真结果如图3所示。

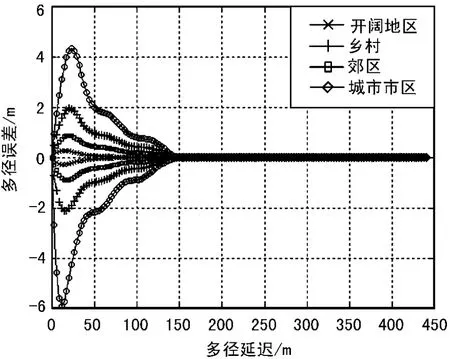
图3 简单多径模型多径误差包络曲线

比较图2和图3,图3的最大值略大于图2,多径持影响续时间略比图2长,包络面积比图2略大。图3中4种环境下分别可以抑制多径85.2%、84.2%、84.2%、84.5%。图 2和图3虽然存在差别,图3可以反映出多径与环境的关系与对信号的影响,在分析信号多径抑制时,为分析方便,可以采用简化随机信道多径模型对应的简单多径误差包络曲线进行信号性能的评估。

4 结束语

基于简单多径模型提出与环境相关的多径模型进行分析,并分析了与环境相关的多径误差包络曲线。该曲线在一定程度上反映了实际多径环境下多径对接收机的影响。环境相关的多径误差包络曲线为分析实际环境中多径对接收机的实际影响提供评估参考意义,为合理计算环境/接收机联合的多径误差提供必要性。

[1]PATZOLD M.Mobile Fading Channels[M].北京:电子工业出版社,2009.

[2]BRAASCH M.Multipath Effects,In:GPS Positioning System Theory and Applications[J].Progress in Astronautics and Aeronautics American Institute of Aeoronautics and Astronautics,1996,163(1):547-568.

[3]KELLY J M.Characterization of the Effects of High Multipath Phase Rates in GPS[J].GPS Solutions,2003,7(1):5-15.