运行速度计算方法比较及验证

林亚萍 陈 飞 陈春红

以运行速度为基础的线形设计方法在国外得到了广泛的运用。运行速度设计法由于在提高公路设计安全性方面具有重大意义，已经引起了我国交通主管部门和专家学者的关注。

1 运行速度简介

1.1 运行速度的引入

近40年，随着汽车制造业的发展，汽车的行驶速度与“设计速度”有了很大差别。事故率和破坏严重性的相应增加暴露了“设计速度法”的固有缺陷。因此，越来越多的西方国家考虑并实行运行速度设计法。我国亦在JTG B01-2003公路工程技术标准、《新理念公路设计指南》(2005版)及JTG/T B05-2004公路项目安全性评价指南(简称《指南》)中引入了运行速度的概念，并建议在速度变化路段、爬坡车道、超高等受限制路段进行运行速度检验[1-3]。

1.2 运行速度确定方法

已建公路的运行速度可通过实测得到;但在新建公路项目的设计阶段是无法以观测的方法得到运行速度的，而是推算路段运行速度，进而以此为基础，对所设计公路的各项技术指标进行评价。《指南》中介绍了两种计算运行速度的方法:依据数学模型进行速度预测(简称“模型法”);依据图表所示读取路段运行速度(简称“图表法”)。

2 运行速度试算与实测

2.1 试算线形简介

取沪宁高速公路南京连接线为例。该段城市快速路起于中山门，终于绕城公路。道路采用一级公路标准设计，设计速度80 km/h。运行速度分上行和下行两个行驶方向，此处确定从沪宁高速公路下来至中山门为正向行驶方向。由于篇幅所限，本文选取其中一段作为试算路段(如图1所示)，进行正向行驶方向上的运行速度计算，即图1中A点至S点。

本文按已实行运行速度设计法国家的确定原则，将缓和曲线路段视为平曲线的组成部分，统归为同一路段加以考虑。

2.2 “模型法”试算演示

2.2.1 路段划分

以“模型法”中的划分原则进行路段划分。路段1:从A点至D点，曲线半径为830 m。

路段2:从D点至G点，曲线半径为983.963 m。

路段3:从G点至I点，曲线半径为1100 m，视为直线段，路段长度为761.588 m。

路段4:从I点至K点，曲线半径为967.620 m。

路段5:从K点至L点，为直线段，路段长度为450.163 m。路段6:从L点至O点，曲线半径为600 m。

路段7:从O点至P点，为直线段，路段长度为202.136 m。

路段8:从P点至S点，曲线半径为700 m。

2.2.2 初始运行速度V0

《指南》中提出预测路段的初始运行速度V0可通过调查点的现场实测，或按表B(1).0.2-1估算得到。此处结合具体状况确定，本试验路段正向行驶车辆大都是从沪宁高速公路下来，起始路段之前的地形比较平坦，线形指标比较高，故在此取V=90 km/h为初始速度。

2.2.3 各路段的运行速度

1)路段1。根据表1(《指南》中表B(1).0.2-3)所列平曲线上的速度预测模型，选用入口直线—曲线公式推算曲线中部运行速度为:

Vmiddle= －24.212+0.834 ×90+5.729ln830≈89 km/h。

图1 路段平面线形

表1 平曲线上的小客车运行速度预测模型

此为路段1运行速度。选用出口曲线—曲线公式，推算曲线终点位置D点的运行速度为:

2)路段2。选用入口曲线—曲线公式推算曲线中部运行速度为:

此为路段2运行速度。选用出口曲线—直线公式，推算曲线终点位置G点的运行速度为:

3)路段3。根据《指南》中直线段上期望车速计算公式Vs=及表2(《指南》中表B(1).0.2-2)所列值，选用加速度值a0=0.18 m/s2，得出此路段终点位置I点的运行速度为:

表2 平直路段上期望运行速度和推荐加速度值

其他路段的运行速度值计算过程类似，不再赘述，计算结果见表3。

表3 各路段运行速度计算值 km/h

2.2.4 纵坡影响

由于试算路段全线纵坡均小于3%，根据《指南》的规定，其对运行速度的修正为0。

2.3 “图表法”试算演示

2.3.1 路段划分

以“图表法”中的划分原则进行路段划分。

路段1:从A点至L点，视为直线段，路段长度为3643.602 m。

路段2:从L点至O点，曲线半径为600 m，自成一个路段，依据表4(《指南》中表B(2).0.1-1)第二列及第三列所列数值，路段运行速度为110 km/h(为估算值，在测试数据范围以外)[1]。

路段3:从O点至S点，视为直线段，路段长度为677.392 m。

2.3.2 初始运行速度V0

A点驶入速度仍为90 km/h。

表4 路段上小客车的运行速度(节选)

2.3.3 各路段运行速度

1)路段1。计算L点的运行速度，查阅图2(《指南》中图B(2).0.1-1)，已知车速为90 km/h，直线段长约3644 m。由于图中没有相对应长度直线的曲线图，且直线段较长，则推算小客车将在直线段上先作加速行驶，直至其期望速度值120 km/h，而后保持匀速行驶，直至驶出直线段。因此确定路段1终点位置L点运行速度为120 km/h。

图2 直线段小客车的运行速度

2)路段2。计算O点(即路段2终点位置)的运行车速时，查阅图3(《指南》中图B(2).0.1-2)，并沿着曲线半径为600 m的直线向上移，直至与代表车速为110 km/h的曲线相交，然后平移至“离开弯道的速度”轴，读出O点驶离车速为108 km/h。

图3 曲线段小客车的运行速度

3)路段3。计算S点(即路段3终点位置)的运行速度，查阅图2，已知车速为108 km/h，直线段长约677 m，则到达直线终端S点时的运行速度仍约为108 km/h。

2.3.4 纵坡影响

由于路段全线纵坡均小于3%，根据《指南》的规定，其对运行速度的修正为0。

2.4 运行速度实测

2.4.1 测速方法

本文采用国产LDR巡逻式测速雷达进行观测。观测断面的选择主要考虑平面线形变化。观测数量的选择，主要是保证观测结果的可靠性，为此本文在每个观测断面上所观测的车辆数约为70 辆[6，7]。

2.4.2 观测速度

本文对每个断面上随机抽测的70个数据利用数理统计软件SPSS进行数理统计分析，从而得到每个观测断面上85%的车速，并依此作为该观测断面的运行速度，如图4所示。

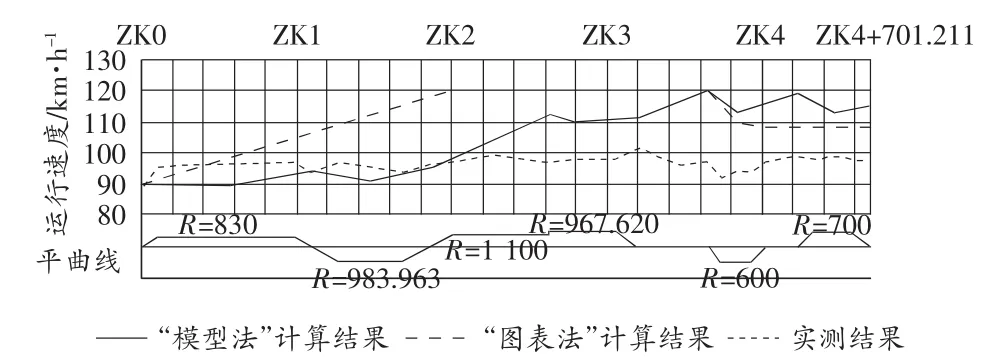
图4 运行速度值比较图

2.5 小结

2.5.1 “模型法”与“图表法”

从试算过程可看出:“模型法”更为可行、合理;“图表法”推算过程简单、直观，读图时却易产生误差;从结果看，就小半径曲线运行速度计算时，两者的计算结果较接近;“图表法”计算过程中，就设计指标较高的公路而言(如该一级公路)，由于较长路段内曲线半径均因大于临界半径值600 m而归为直线段考虑，造成因直线段长度过长，在计算中无据可依，所以可操作性不强，且计算结果粗糙。

2.5.2 试算与实测比较

如图4所示，相较“图表法”“模型法”计算结果较为接近实测值，却在某些路段上存在较大误差，这可能与以下因素有关:

1)模型没充分考虑驾驶员主观期望;

2)与临界值和接近临界值的曲线、短直线段处理方法有关;

3)实测速度值由于受各种因素影响存在误差;

4)样本的代表性，预测路线的特殊性，对预测结果有影响;

5)“图表法”采用澳大利亚运行速度计算法，与我国交通条件有差异。

3 有待进一步研究的问题

3.1 关于临界值和接近临界值的问题

在“模型法”中，对半径为临界值(1000 m)的圆曲线划归没有明确规定。同时“模型法”中有个短直线临界长度值200 m，“图表法”中有个临界半径值600 m，虽然后两者划归有规定，但都有个共同问题，即接近临界值的曲线半径或直线长度的处理。对临界值和接近临界值设计指标的线形按不同方式处理，结果存在较大差异，因此，应在理论基础支持，大量实测数据统计分析或试算验证后，进一步探讨这种情况的处理方法。

3.2 模型的优化及适用性问题

由于运行速度的影响因素繁多，预测模型在建立过程中对这些因素的考虑一般都较理想化，而仅考虑主要因素，且模型的建立受样本特殊性的影响，所以预测的运行速度势必与实际车速存在误差。所以如何建立综合考虑各种影响因素，且适用我国各区域各等级公路的运行速度预测模型，有待进一步研究。

4 结语

国内就运行速度预测模型及运行速度设计法进行了大量的研究工作，并有了一定成果。但理论基础尚需完善，适用于我国公路特点的相关参数及预测模型还需继续研究论证，以期提出适合我国国情的运行速度设计法。

[1]JTG B01-2003，公路工程技术标准[S].

[2]JTG/T B05-2004，公路项目安全性评价指南[S].

[3]中华人民共和国交通部公路司.新理念公路设计指南(2005版)[M].北京:人民交通出版社，2005.

[4]JTJ 011-94，公路路线设计规范[S].

[5]陈胜营，汪亚干，张剑飞.公路设计指南[M].北京:人民交通出版社，2000.

[6]钟小明，荣 建，刘小明，等.高速公路弯坡路段小客车自由流运行速度模型研究[J].公路交通科技，2004，21(12):84-88.

[7]周荣贵，孙家凤，吴万阳，等.高速公路纵坡坡度与运行速度的关系[J].公路交通科技，2003，20(4):34-37.