基于不同几何模型的感应式磁声成像声源重建仿真

马虹霞 刘志朋 张顺起 殷 涛

(中国医学科学院 北京协和医学院 生物医学工程研究所，天津 300192)

引言

生物电阻抗成像技术［1－3］是近年发展起来的新型功能成像技术，它根据人体组织在不同生理和病理状态下具有不同的电阻(导)率，通过给人体施加安全驱动电流(电压)，在体外测量响应电压(电流)信号，以重建人体内部的电阻(导)率分布和变化的图像。生物电阻抗成像对组织电阻(导)率的变化具有较高的检测灵敏度和对比度，对疾病的早期诊断具有较明显的优势，但空间分辨率较低的弱点限制了其在临床上的深入应用。为提高空间分辨率改善重建图像的质量，He等于2005年提出了一种新的组织功能成像技术—感应式磁声成像［4－5］(MAT-MI)。感应式磁声成像兼具电阻抗成像高对比度和超声成像高空间分辨率的优点，其基本原理是将目标物体置于静态磁场中，施加磁脉冲激励在目标物体中感应出涡电流，涡电流与静磁场作用产生洛伦兹力，带电粒子受到洛伦兹力产生声振动，由声探头检测声信号，通过图像重建得到由声信号携带的组织电导率分布与变化信息。

近年来感应式磁声成像作为一种新型功能成像技术备受关注，目前已有该方面的相关报道［6－15］，但是大多数研究都是建立电导率突变的规则模型并且假设激励磁场空间分布均匀。由于生物组织结构复杂，电磁场正问题中很难得到感应涡流的解析解，并且组织电导率分布并非严格跃变，而是存在一定的过渡带。因此，本研究从不规则的几何模型出发，建立了具有一定尺寸的圆形单线圈以及正方体、偏心球、椭球和电导率连续分布的球模型，应用有限元分析软件 Comsol 3.5a，计算了具有不同电导率模型中的感应涡流，利用 Matlab软件工具根据有限元分析的数据，仿真计算了模型的声源分布及逆问题重建所需的空间声压序列，应用时间反演方法重建了能够反映不同电导率边界的声源图像信息。实际应用中，由于客观条件的限制，声探头扫描范围有限，很难得到完备的测量数据，因此，本文最后还定性分析了探测器检测范围的有限性对重建声源图像的影响。

1 理论方程

感应式磁声成像是一种多物理场耦合的新型功能成像方法，涉及到电磁学、力学和声学知识，研究MAT-MI可以分为正、逆问题两个方面，正问题已知样本电导率分布求解声源及声信号，逆问题是已知声信号通过相应的重建算法求解声源进而得到样本的电导率。

1.1 正问题

感应式磁声成像产生的声信号满足如下波动方程［4］

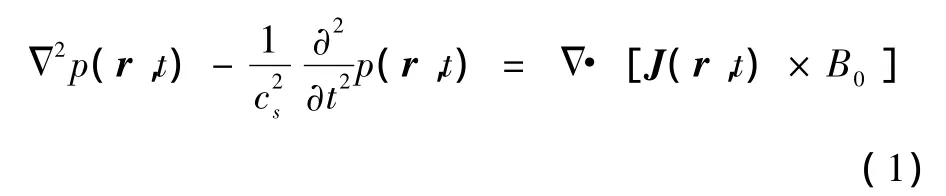
式中，cs是声在组织中传播的速度，p(r，t)是产生的声波，J(r，t)是感应涡流密度，r为被检组织内一点，Δ·(J(r，t)×B0)是声振源。对于波动方程右侧的声振源可通过电磁场理论获得，经典麦克斯韦方程组为

本构关系为

式(2c)表明磁通密度B是无散的，可表示成矢量磁位A的旋度，即有

将式(6)代入(2a)，有

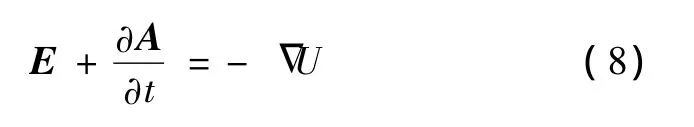
亦即

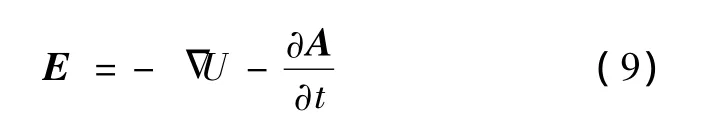
在准静态情况下，位移电流相对传导电流可以忽略，将式(3)、(5)、(6)和式(9)代入式(2b)得到

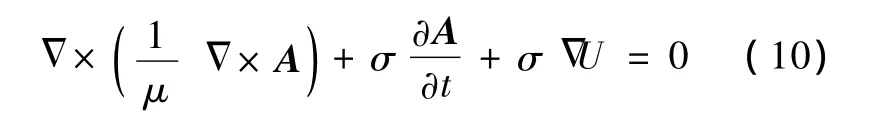
由于样本内无外部电流源，并且生物电流远小于感应涡电流，根据电流连续性定理，有 Δ·J=0，即

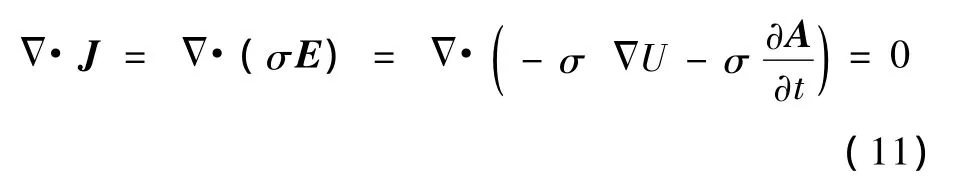
因此，式(10)和式(11)构成求解目标物体中感应涡流的控制方程。当激励磁场脉宽足够窄时，通过格林函数法求波动方程(1)得到声压的表达式为［4］

式中，rd为传声器检测面上一点，Ω是声传感器检测面。通过有限元法求解感应涡流后，由式(12)便可获得MAT-MI产生的声信号，再利用此声压信号进行逆问题声源图像的重构。

1.2 逆问题

假设激励脉宽足够窄时，感应涡流可近似为J(r，t)=J(r)δ(t)，在时间域(－ ∞ ，0+)上对波动方程两边进行积分得到= Δ·(J×B0)，由声场中的时间反演法可以得到声源的重建公式为［4］

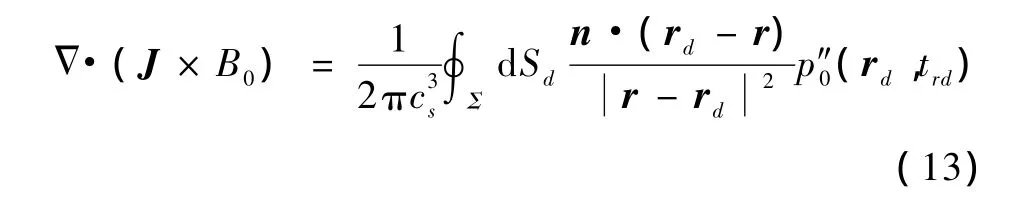
式中，Σ是传声器检测面，r是被检测组织内的一点，n是Σ平面上rd处的单位矢量。

2 仿真方法

考虑实际情况中生物组织结构和电导率相对复杂，本研究从不规则的几何模型出发，分别建立了圆形单线圈激励下的偏心球、正方体、椭球及电导率沿径向呈余弦连续分布的球模型。在直角坐标系 x，y，z中，线圈平面平行 xoy，位于 z=0.1 m处。线圈半径R=0.1 m，线圈截面半径r=0.002 5 m，激励磁场脉宽为2 μs。静态磁场沿着 z方向均匀分布，仿真模型参数如表1所示。

表1 模型参数Tab.1 Model parameters

建立数学模型后，应用有限元分析软件Comsol 3.5a对模型求解域进行离散剖分，施加电磁场边界条件，采用伽辽金加权余量有限元方法建立方程组，求解方程组得到模型中的感应涡流。利用有限元分析结果，叠加空间均匀分布的静态磁场，进一步得到洛伦兹力的散度即声振动源，应用Matlab软件工具进行模拟声场的计算和声源重建工作。对声场的仿真，假设组织的声学特性均匀，声波在传播路径上没有散射和衰减，由式(12)求解得到模拟声场。本研究在仿真过程中把空间固定位置处的声压随着时间的变化，都相应地转化为声压随传播距离的变化进行计算，此处传播距离实际为声速与时间的乘积。同时假设声探测器在检测断面上以原点为中心呈环形均匀离散分布，用来检测不同位置接收的声压信号，最后应用时间反演式(13)进行声源图像的重建仿真。由于实际进行成像时，很难检测到所有位置处的声压信号，因此本研究最后还进行了有限角度扫描下的声源重建仿真，分析了检测范围的有限性对重建声源图像的影响。

3 结果与分析

3.1 不同模型声源分布

通过对不同模型的仿真，选取z=0平面显示仿真结果。图1为原始电导率在z=0平面分布，(a)～(d)分别代表偏心球、正方体、椭球、连续球模型，后续内容中字母与图的对应关系与此处相同。图2为不同模型声源在z=0平面分布，对于电导率非连续分布的偏心球、正方体、椭球、连续球模型，在电导率跃变的边界，感应涡流较大，受到的洛伦兹力较大，相应的声振动源也大，声源的平面分布能够明显地区分模型的边界。从图3的曲线中也可以看出，与电导率相同的内部声源相比，边界声源要大很多，因此，在这种强对比情况下，声源几乎仅能反映模型的基本几何轮廓。对于电导率呈余弦分布的连续同心球模型，由于电导率呈缓慢地连续变化，从z=0平面声源沿x轴的分布曲线可以看出，声源没有出现类似于前面3种模型边界有较大跳变的情况，变化相对平缓，仿体组织边界区分不明显。生物体不同组织的电导率实际上也存在一定过渡带，并不是严格跃变的，分析连续电导率模型对后期建立更加真实的组织模型有一定指导意义。

3.2 检测声压随距离的变化

图1 原始电导率分布。(a)偏心球;(b)正方体;(c)椭球;(d)连续球Fig.1 Target conductivity distribution.(a)eccentric sphere;(b)cube;(c)ellipsoid;(d)continuous sphere

图2 声源在z=0平面分布。(a)偏心球;(b)正方体;(c)椭球;(d)连续球Fig.2 Acoustic source distribution in z=0 plane.(a)eccentric sphere;(b)cube;(c)ellipsoid;(d)continuous sphere

将位于检测面上x轴固定点处的声探头接收的声信号随着时间的变化曲线转化为声压与距离的关系，如图4所示，横坐标的距离代表着声速与对应时间的乘积。图5为探测器接收的声信号是以探测器位置P为原点，以R为半径关于声源的弧线l积分，对于电导率非连续分布的偏心球、正方体和椭球模型，从声压信号分布曲线可以看出，声压信号幅值发生较大变化的位置对应着模型电导率变化的边界。以偏心球为例，声压曲线出现了4个尖峰，中间的两个尖峰之间的距离对应着内层球的直径，外边两个尖峰的间距对应着外层球的直径，第一个和第二个尖峰的间距对应着内外层球边界的距离。对于电导率呈余弦连续分布的球模型，声源变化缓慢，因此，探测器接收的声压信号没有出现较大的突变，变化也较为平缓。

3.3 声源重建

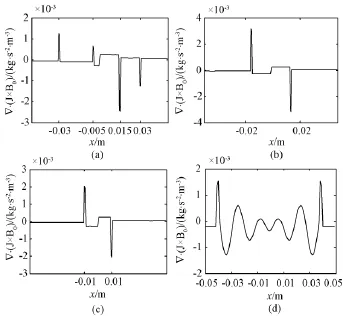
图3 声源在z=0平面沿x轴分布。(a)偏心球;(b)正方体;(c)椭球;(d)连续球Fig.3 Acoustic source distribution along x axis in z=0 plane.(a)eccentric sphere;(b)cube;(c)ellipsoid;(d)continuous sphere

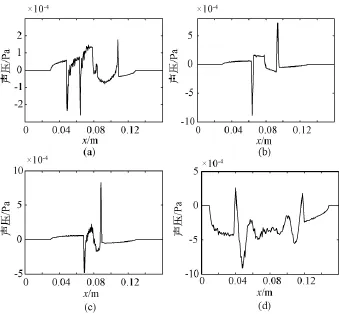
图4 x轴正方向一个声探头检测的声信号。(a)偏心球;(b)正方体;(c)椭球;(d)连续球Fig.4 Pressure distribution with one detector located in x forward direction.(a)eccentric sphere;(b)cube;(c)ellipsoid;(d)continuous sphere

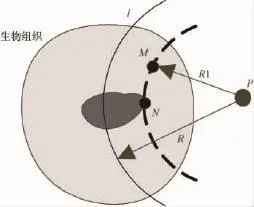
图5 投影示意图Fig.5 The projection diagram

由声场中的时间反演方法即式(13)进行声源重建得到的图像如图6所示。对电导率非连续分布模型，由于声压信号幅值的较大变化对应着电导率变化的边界，根据重建理论公式，反投影后边界声源相对内部声源大，使得内外两层球重建声源区分不够明显，重构的声源图像基本显示了物体的边界轮廓。对于电导率呈连续分布的球模型，声压信号变化平缓，反投影后的重建声源平面图不仅再现了模型的几何形状，同时还体现了声源缓慢变化的特点。对于不连续模型，可以预先滤除幅值较大的边界信号，通过内外层图像的反差来显示边界轮廓;而对电导率连续分布的模型，不存在跃变现象，可以通过增加采样点获得较好的重构效果。由理论公式(13)可知时间反演法的实质是投影数据沿着弧线的直接反投影重建算法，声源图像的像素值是所有反投影数据在该位置处的叠加，如图5所示，声源M和N到探测器P的距离相等，当把声信号反投影到非边界声源M时，由于声压信号叠加了具有较大幅值的边界声源N，使得反投影后M和N点得到了一个相同的投影数据叠加项，从而导致了重建图像声源的模糊效果，后期可以通过先修正后反投影的滤波反投影重建方法改善图像质量。

图6 重建声源在z=0平面分布。(a)偏心球;(b)正方体;(c)椭球;(d)连续球Fig.6 Reconstruction acoustic source distribution in z=0 plane.(a)eccentric sphere;(b)cube;(c)ellipsoid;(d)continuous sphere

3.4 探测器检测范围对重建图像的影响

声振动源较好反映了模型的几何结构，以重建模型基本轮廓为目的，还分析了探测器检测范围的有限性对重建图像的影响。图7是探测器以坐标原点为中心，均匀分布在圆周检测断面(0，π/2)范围内得到的重建图像，可以看出，由于扫描角度有限，重建模型边界有些也完全失真。分析声源重建式(13)，得知声压二阶导数前面相乘了一个比例因子，当声源位于探测器的法线方向时，比重最大，偏离法线方向，比重较小。因此，对于有限角度扫描的情况，能有效重建的位置取决于比例因子和探测器的扫描范围。在环形扫描模式下，两个测量位置的角度差为π时，投影值呈反相关系，对重建声源是等效的，因此，在图6中真实再现边界轮廓的范围还包括角度差为π的边界点，该处法线方向也覆盖了(0，π/2)范围内的声探测器。

图7 不完全数据重建声源在z=0平面分布。(a)偏心球;(b)正方体;(c)椭球;(d)连续球Fig.7 Reconstruction acoustic source distribution in z=0 plane with incomplete data.(a)eccentric sphere;(b)cube;(c)ellipsoid;(d)continuous sphere

4 讨论和结论

本研究从不规则的简单几何模型出发，建立了偏心球、正方体、椭球和电导率连续分布的球模型，应用有限元分析方法对模型中感应涡流进行仿真，采用Matlab软件工具求解声压来模拟逆问题中的声压数据，通过时间反演法重建了不同模型的声源图像，同时还重建了有限角度扫描下的声源图像。从仿真结果可知，不同参数的几何模型，探测器接收的声信号差异较大，为获得高质量的重构图像，对于不连续模型，可以预先滤除边界跃变来提高内外两层球的声源对比度;而对电导率连续分布的模型，不存在跃变现象，可以通过增加采样点获得较好的重构效果。应用有限元和时间反演法能够重构声源图像，但本研究重建的图像存在明显的弧线伪迹，这与采用的直接重建算法有关，为了减少或消除伪迹对图像质量的影响，需要进一步寻求更高效的算法。实际情况中很难得到完备的投影数据，有限角度扫描仿真结果表明，直接采用本研究的重建算法，检测范围的有限性会使重建图像失真，因此也有必要探索新的算法来完善更为接近实际成像条件下的图像质量。生物组织的电导率分布并非严格跃变，研究电导率连续分布的球模型对磁声成像的实际应用提供了较好的理论基础，但是需要进一步建立更为真实的生物组织电导率连续分布模型。由于目前只是定性分析了声源图像的重建工作，后期对于感应式磁声电导率成像还需要深入地进行定量地探索，从而重建出能够反映生物组织电特性的图像。

［1］安源，任超世.电阻抗断层功能成像技术的发展［J］.第四军医大学学报，2001，22(1):90－92.

［2］董秀珍.生物电阻抗成像研究的现状与挑战［J］.中国生物医学工程学报，2008，27(5):641－643，649.

［3］Bayford RH.Bioimpedance tomography［J］.Annu Rev Biomed Eng，2006，8:63－91.

［4］Xu Yuan，He Bin.Magnetoacoustic tomography with magnetic induction［J］.Phys Med Biol，2005，50:5175 －5187.

［5］Li Xu，Xu Yuan，He Bin.Magnetoacoustic tomography with magnetic induction for imaging electrical impedance of biological tissue［J］.Appl Phys，2006，99:066112.

［6］Xia Rongmin，Li Xu，He Bin.Magnetoacoustic tomographic imaging of electrical impedance with magnetic induction ［J］.Applied Physics Letters，2007，91:083903.

［7］Li Xu，Xu Yuan，He Bin.Imaging Electrical impedance from acoustic measurements by means of magnetoacoustic tomography with magnetic induction(MAT-MI)［J］.IEEE Trans Biomed Eng，2007，54(2):323－330.

［8］Ma Qingyu，He Bin.Investigation on magnetoacoustic signal generation with magnetic induction and its application to electrical conductivity reconstruction ［J］. Phys Med Biol，2007，52:5085－5099.

［9］张媛.磁感应磁声成像的声源产生机制［J］.湖州师范学院学报，2009，31(1):70－75.

［10］李珣，Li X，朱善安，等.基于时间反演方法的三维磁感应磁声成像电导率重建［J］.中国生物医学工程学报，2009，28(1):48－52.

［11］贺文静，刘国强，张洋，等.感应式磁声成像声场正问题研究(一)—基于声压速度耦合方程的声场模拟方法［J］.现代科学仪器，2010，(1):9－13.

［12］刘国强，贺文静，夏慧，等.感应式磁声成像声场正问题研究(二)—基于位移方程的声场模拟方法［J］.现代科学仪器，2010，(1):14－16，23.

［13］刘国强，贺文静，夏慧，等.感应式磁声成像声场正问题研究(三)—基于弱形式处理洛伦兹力散度声源的声场模拟方法［J］.现代科学仪器，2010，(1):17－20.

［14］许国辉，刘志朋，李经宇，等.感应式磁声成像正问题数学模型及仿真［J］.中国生物医学工程学报，2009，28(4):481－484，489.

［15］李经宇，殷涛，刘志朋，等.基于磁声耦合效应的电导率图像重建研究［J］.生物医学工程学杂志，2010，27(2):416－420.