应用于头部损伤生物力学研究的三维有限元模型发展概况

赵 玮 阮世捷 李海岩

(天津科技大学损伤生物力学与车辆安全工程中心，天津 300222)

引言

交通损伤成为威胁人类安全的主要社会因素之一。头部损伤因其较高的致命性，已成为最严重的交通损伤。据统计，全球15%的交通事故发生在中国，每年十万人的死亡相当于每天有三百人。随着汽车保有量的逐渐增加，未来几年中国的交通损伤存在着有增无减的趋势。行人、自行车、机动车之间的相互碰撞不可避免地频繁出现，由此引发的头部损伤必然会大大增加。因此，研究、探讨、理解头部损伤中的生物力学问题，研究头部损伤在交通事故中的损伤机理，对于制定相应的防护措施和降低伤害的发生率具有非常重要的意义［1－2］。

目前，研究头部生物力学响应的主要手段包括物理模型试验［3－5］、动物模型试验［6－18］、尸体模型试验［19－22］。尽管物理试验成本较低，在某种程度上可以观察到结构受到载荷时的物理现象，但是物理模型在材料的选用及其生物逼真度方面仍然具有一定的局限性。另外，物理模型毕竟不是生物模型，不能观察到生物体的生理病理学变化;尽管动物模型可以观察到由于承受载荷引起的病理生理学变化和组织破坏，但是，就输入与响应的因果关系而言，从动物试验所得到的数据直接通过外推法换算到人体［12］，在统计学意义上、数学意义上和试验技术上显示出一定的局限性。另外，研究者们现在也只是通过量化的方法来确定动物脑部与人体脑部承受载荷时响应的不同;虽然尸体单个样本的特征不能代表全部样本，但是其响应趋势能在一定程度上说明问题。尽管尸体可以提供与活人相同的几何结构和解剖学特征，但是尸体试验却不能观测样本由于受到载荷，尤其是加速度载荷，而引起的生理病理学变化和组织破坏，这也显示出了尸体试验具有一定程度的局限性。

由于物理试验、动物实验和尸体试验存在着上述局限性，随着计算机技术的不断发展，有限元模型逐渐成为了研究头部损伤生物力学的重要工具。文中将从应用于头部损伤生物力学研究的有限元模型构建、验证有效性以及参数化研究等方面对相关文献进行综述。

1 三维有限元模型的研究进展

在过去的40年中，研究者构建出了许多版本的有限元模型。Hardy和 Marcal于1971年构建了第一个具有真实几何形状的人体头部有限元模型，该模型被用于做静态仿真［23］。1975年 Ward和Thompson构建了一个接近真实脑部结构的有限元模型用来模拟尸体头部试验。在该模型中，脑部由189个八节点实体单元构成，硬膜、大脑镰和小脑幕由80个四节点壳单元构成，颅骨被视作刚体，脑脊液为线弹性材料，其弹性模量与泊松比分别为31.5 MPa和0.48，脑组织为弹性材料，其弹性模量和泊松比分别为 650 kPa 和 0.489［24］。

Shugar于1977年构建了一个用于进行碰撞仿真的模型。该模型的颅骨与脑组织之间用一层实体单元来表示蛛网膜下空间，最后通过与充满水的物理模型在相同载荷条件下的压力值对比来验证模型的有效性，研究表明，在相同的载荷条件下，有限元计算得到的压力值是物理模型压力值的10倍左右［25］。

1980年Hosey和Liu构建了一个由637个实体单元和149个壳单元构成的头部有限元模型，其研究目的在于模拟碰撞处对侧的空穴现象并与Nahum尸体头部碰撞试验的颅内压数据作对比验证了有效性。该模型的颅骨选用线弹性材料，其弹性模量和泊松比分别为4.46 GPa和0.21，脑脊液选用线弹性材料，其弹性模量和泊松比分别为66.7 kPa和0.499脑组织的材料属性同脑脊液，膜结构选用线弹性材料，其弹性模量和泊松比分别为31.5 MPa和0.45［26］。

Dimasi于1991年构建了一个三维头部有限元模型用来模拟加速度为165～302 g时有阻尼的与无阻尼的头部撞击。该模型共有500个单元，颅骨选用线弹性材料，其弹性模量为2.4 GPa，脑组织选用粘弹性材料，其短效剪切模量、长效剪切模量、延迟系数和体积模量分别为34.5 kPa、17.2 kPa、100 s－1和68.95 kPa，大脑镰与小脑幕均选用线弹性材料，其弹性模量为 6.89 MPa［27］。

1992年，Mendis构建了两个有限元模型用以分析当头部受到旋转加速度时，脑组织应力与应变并且与Gennarelli和Thibault在灵长类动物试验［28］中所测得的与轴索损伤严重程度有关的脑组织应变作比较。随后，这些仿真的结果通过外推法换算到人头部，该模型的脑组织选用超弹性材料，该超弹性材料的本构方程［29］为

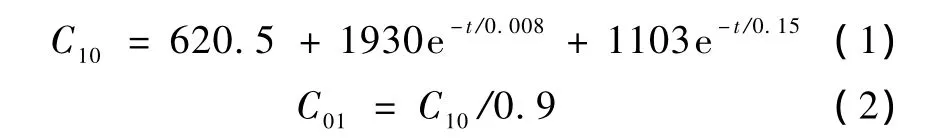
式中，C10与C01分别为Mooney-Rivlin刚度系数。

另外，在1977年到1993年之间还有一些版本的有限元模型，例如，1982年 Ward的［30］，1982年Khalil 和 Viano 的［31］，1993 年 Sauren 和Claessens 的［32］。

随着计算机技术的飞速发展，研究者们构建出越来越复杂的有限元模型并为研究由于碰撞而产生的脑损伤提供有利的信息。

1.1 WSU(Wayne State University)Model I

1994年，Ruan等构建了一个结构较为详细的有限元模型，如图1所示，该模型为第50百分位头型，总共6 080个节点和7 351个单元，其中包括头皮864个单元、颅骨2 800个单元、脑1 760个单元、脑脊液864个单元、硬脑膜896个单元和大脑镰135个单元，脑组织选用粘弹性材料，总质量3.077 kg，其中脑组织质量 1.25 kg。该模型重构了 1977年Nahum的尸体头部撞击试验［19］，其颅内压力与试验吻合良好。除了验证模型的有效性，Ruan等还在此基础上进行一系列的参数化研究，结果表明，模型受到枕骨处撞击时，颅内对撞侧压力较其受到前额撞击时的高。随着颅骨弹性模量的增加，颅内撞击侧压力减小，对撞侧压力升高。随着脑脊液体积模量的增加，颅内撞击侧压力升高，对撞侧压力减小［33］。

2007年，Ruan等对现有的头部损伤判断准则适用性和可用性进行了新探索［34］。该研究分别对不同尺寸的头部有限元模型在相同加速度情况下的生物力学响应进行研究，结果表明，用HIC值来衡量直接撞击情况下头部损伤的可能性具有一定的科学性和可靠性;头型的大小、头部质量的大小对头部受损伤的可能性的判断有较大影响，不应用同样的HIC值来衡量所有人头部受损伤的可能性，对质量(或尺寸)较大的头型应用低于平均的HIC值，对质量(或尺寸)较小的头型则可用高于平均的HIC值。

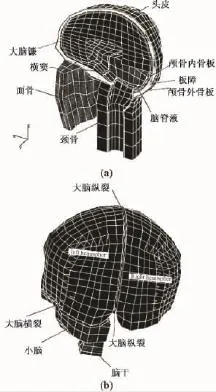
图1 韦恩州立大学模型 I［19］。(a)头部有限元模型;(b)颅脑左右半球有限元模型Fig.1 WSU model I［19］.(a)finite element of human head;(b)right and left hemisphere of human head

1.2 WSUBIM(Brain Injury Model)

1995年Zhou等在Ruan等模型的基础上进行改进构建了一个具有详细颅内结构的脑损伤模型，如图2所示。该模型为第50百分位头型，其结构包括头皮、颅骨、硬脑膜、大脑镰、小脑幕、软脑膜、脑脊液、静脉窦、脑室、区分灰、白质的大脑、小脑、脑干和桥静脉，总共17 656个节点，22 995个单元，总质量为 4.37 kg，其中脑组织质量为 1.41 kg。与Ruan的头部有限元模型相比，由于该模型区分了脑组织的灰、白质，因此能够更精确地利用几何形状和本构关系模拟不均匀的脑组织特征。由于模型构建了脑室和桥静脉，则可以估计硬膜下血肿的发生，另外还细化了脑组织部分的网格。同 Ruan的模型一样，该模型也与Nahum尸体头部撞击试验进行了对比来验证模型的有效性［19］，但是由于模型计算所得的对撞侧压力较试验值高10%，因此该模型被认为是部分有效。随后，该模型还用来研究头部受到矢状面内旋转加速度时的生物力学响应。结果表明，撞击侧和对撞侧的损伤可能是由于颅内压力引起的，而胼胝体和脑干的损伤可能是由于切应变引起的。胼胝体膝处的切应力可以认为是预测弥漫性轴索损伤的指标。桥静脉的响应也与动物试验中硬膜下血肿的发现吻合良好。对于桥静脉拉伸应变的估计表明，在前额受到撞击以后，脑组织的回弹阶段存在着潜在的桥静脉断裂危险。这是第一次用有限元模型模拟桥静脉，并通过这些桥静脉来研究硬膜下血肿的损伤机理［35］。

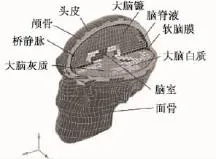
图2 韦恩州立大学脑损伤模型［35］Fig.2 WSU brain injury model［35］

1.3 WSU Final Version

2001年，Zhang等为了研究头部的高强度直接撞击和间接撞击，构建了一个更完善的头部有限元模型，如图3所示。该模型是基于先前的WSU模型经过修改细化网格构建而成的，其尺寸属于第50百分位，其中包括头皮、颅骨内、外骨板、板障、硬脑膜、大脑镰、小脑幕、软脑膜、矢状窦、横窦、脑脊液、区分大脑白质与灰质的大脑半球、小脑、脑干、侧脑室、第三脑室、桥静脉以及包括下颌骨、上颌骨、颧骨和鼻骨在内的面骨，总共281 800个节点和314 500个单元，总质量为4.5 kg，脑组织的材料属性为粘弹性，面部的密质骨与松质骨为弹塑性材料［36］。此模型已经重构出了53例体育运动事故，其中包括发生脑震荡的22例。

Zhang等还提出一种新的验证头部有限元模型有效性的方法，即，与行人碰撞的交通事故损伤数据作对比［37］。研究结果表明，该模型可以用来模拟真实情况下行人的头部碰撞，另外，在一般情况下，还可以通过最大主应变来预测弥漫性轴索损伤;利用该模型还可以通过仿真来检验韦恩曲线，当HIC值为1 000时，对应的最大主应变大约为0.2。

1.4 ULP(Université Louis Pasteur)模型

图3 韦恩州立大学最终版模型［37］Fig.3 Final version of WSU model［37］

Kang和Willinger于1997年构建了 ULP模型，如图4所示。该模型包括头皮、颅骨的内、外骨板、大脑镰、小脑幕、脑脊液、大脑、小脑以及脑干。为了估计颅骨的骨折，颅骨选用弹性脆性材料。脑组织为粘弹性材料，脑脊液选用弹性材料，头皮、面骨、大脑镰和小脑幕全都选用均匀的各向同性材料。该 ULP模型共包含13 208个单元，总量为4.7 kg［39］。

该模型通过与 Nahum尸体头部撞击试验［19］、Trosseille尸体撞击试验［20］和 Yoganandan的颅骨断裂试验［21］的对比来验证有效性［38］。与 Nahum 试验［21］相比，仿真所得的头部加速度最大值比试验所得的约小20%，颅内压力曲线与试验所得曲线吻合良好。然而，与 Trosseille试验［20］相比，颅内压力曲线与试验所得曲线存在着一定差异。与Yoganandan的试验［21］相比，通过有限元仿真得到的失效力—位移曲线在试验所得范围之内，从而证明了该模型的有效性［39］。另外，该模型还被用来与Hybrid III假人连接进行假人跌落仿真和重构摩托车交通事故中的头部撞击［39］。

1.5 TUE(Eindhoven University of Technology)模型

1997年，Claessens等构建了一个包括颅骨、脑、面骨和颅内膜结构的头部有限元模型，如图5所示。其几何形状由CT图像提取，利用“投影”方法划分脑组织网格，颅骨是由脑组织表面的网格拉伸而成，模型共计1 756个六面体单元和2 257个节点，模型所有结构均使用均匀的各向同性线弹性材料。但是其初始尺寸是第95百分位的，将其缩小到第50百分位以后，通过模态分析和与Nahum尸体头部撞击试验进行对比验证有效性［19］。验证结果表明，尽管颅内压力尤其是撞击对侧的负压力，较试验值高，但就其趋势而言，能在一定程度上说明模型具有有效性。然而该模型的仿真结果与试验结果的差异还不能通过特定的模型说明［40］。

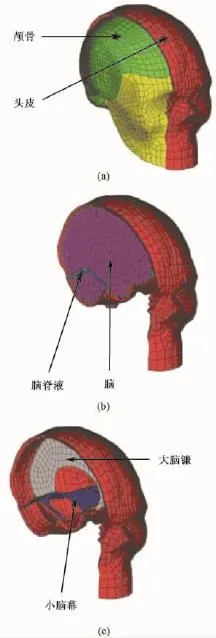
图4 路易斯巴斯德大学模型［39］。(a)颅骨;(b)脑组织;(c)颅内被膜Fig.4 ULP model［39］.(a)skull;(b)brain tissue;(3)intracranial membrane

2002年，Brands等对 Claessens版本的 TUE模型进行了改进，共计14 092个六面体单元，其解剖学结构包括颅骨、被膜结构和脑脊液、脑组织三个部分。该模型被用来研究在受到前后方向的旋转时，非线性材料对脑组织相应的影响。结果表明，非线性材料的选用可以使偏应变增加将近21%，使应力减小11%;颅内压力与非线性材料的选用无关，压力梯度完全取决于模型在承受载荷过程中是否动量守恒而与脑组织的本构模型无关［41］。

1.6 KTH(Kungliga Tekniska Högskolan)模型

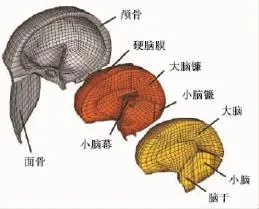
图5 埃因霍温科技大学模型［40］Fig.5 TUE Model［40］

2002年，Kleiven等人构建如图6所示的第50百分位成人头部有限元模型［42］，包括头皮、颅骨、脑、被膜、脑脊液和11对侧矢状面桥静脉。另外，模型中还构建了简化的颈部结构，包括从脑干到脊髓的部分、硬膜、椎骨以及周围的皮肉组织。颅骨的内、外骨板、板障、面骨、头皮、大脑、小脑、脊髓、硬脑膜、小脑幕和大脑镰，模型总共18 400个单元。为了应对较大的弹性变形，模型的中枢神经系统采用Mooney-Rivlin本构方程［43］，另外，通过引入与粘性应力线性相关的弹性应力，利用粘弹性性质来考虑耗散作用。在仿真中，该模型的颅骨与脑组织之间分别被设置了不同的接触面来模拟脑组织相对于颅骨的移动。结果表明，在低强度撞击情况下，颅骨与脑之间接触的定义不会对二者之间的运动产生显著影响。研究中使用了一系列的剪切刚度值，但是，颅—脑的相对运动只对脑组织材料属性非常敏感。侧面撞击时颅—脑的相对运动程度较前额撞击和枕骨撞击时的小。为了准确预测头部受撞击时的局部脑组织响应，脑组织应使用较小的剪切刚度值。

该模型还通过缩放方法被缩小到第5百分位和放大到第95百分位尺寸，进行不同尺寸之间脑组织响应的研究［44］。结果表明，在相同的加速度载荷下，脑组织的等效应力范围从质量最小头部的6.3 kPa到质量最大头部的16.3 kPa。在使用填充材料模拟头部碰撞时，头部HIC值的最大值2 433出现在质量为2.4 kg的头部，最小值1 376出现在质量为5.98 kg的头部。HIC值不能预测这种与头部质量有关的颅内应力，在制定新的头部损伤准则时应考虑头部尺寸。

1.7 UCD(University College Dublin)模型

Horgan和 Gilchrist于2003年构建了一个新型第50百分位三维头部有限元模型，如图7所示，用来模拟行人碰撞事故［45］，并与 Nahum试验进行对比验证了有效性［19］，与此同时还进行了一系列参数化研究，例如，不同密度的网格对模型响应的影响，颅骨使用壳单元对模型响应的影响和脑组织材料属性对模型响应的影响。研究结果表明，神经组织的短效剪切模量对模型撞击侧颅内压力和Von Mises应力的影响最大。若将脑脊液与颅骨之间定义耦合结点，则脑脊液的体积模量对对撞侧的压力有显著影响。

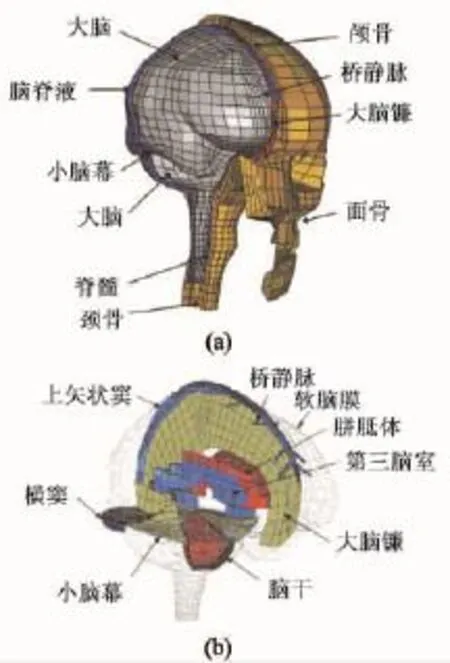
图6 瑞典皇家工学院模型［42］。(a)颅骨及脑组织;(b)被膜结构及脑室Fig.6 KTH model［42］. (a)skull and brain tissue;(b)intracranial membrane and ventricles

为了研究模型材料的本构属性、模型的几何形状和脑组织的形状对头部碰撞损伤机理的影响，Horgan和Gilchrist于2004年对UCD模型进行了改进，并与一系列的尸体试验进行了对比验证有效性［20，22，46］。该研究构建了 6 个有限元模型，分别为(1)基准模型;(2)在基准模型的基础上区分脑组织的灰、白质的模型;(3)脑脊液沿着厚度方向被构建为三层单元的模型;(4)在颅骨与脑之间设置可以相对滑动接触面的模型;(5)用投影方法构建的模型，仍然区分脑组织的灰、白质;(6)经过拓扑修型后的模型。结果表明，该六组模型与Trosseille试验进行对比［20］，颅内压力都有一定程度上的差异，区分灰、白质的模型与试验结果最接近，定义滑动接触面模型的颅内压力与试验结果差别较大，这可能是由于计算接触时使用了惩罚接触方程，经过拓扑修型后的模型也与试验结果有差别，可能是由于头部形状以及前后长度等微小的差异所导致。当六组模型与Hardy试验进行对比时［22］，对基准模型进行改进并不会使基准模型具有更好的预测能力。区分灰、白质就意味着更多的单元需要更全面的解剖学材料属性，由于构建了脑室，则能够观察其周围边角处的应力集中。

图7 都柏林大学模型［45］。(a)脑与颅骨;(b)脑脊液与颅骨Fig.7 UCD model［45］.(a)brain and skull;(b)CSF and skull

1.8 湖南大学 HBM(Human Body Model)头部模型

2008年，许伟等基于美国人三维解剖学图像数据构建了第50百分位头部有限元模型，如图8所示。HBM头部模型描述了主要的解剖学结构，包括头皮、颅骨、硬脑膜、脑脊液、软脑膜、大脑、小脑、脑室、脑干、大脑镰和小脑幕等组织结构，模型共计66 624个节点，49 607个实体单元和11 514个壳单元组成，质量为4.4 kg。HBM模型中定义硬脑膜紧贴在脑颅的内表面，而软脑膜附着在脑表面。通过tied-contact接触定义对这种附着特性进行模拟，使用滑动接触来模拟脑脊液层和硬脑膜之间的相对运动。为了减少模型的复杂程度，脑室与脑使用共结点。该模型通过与Nahum试验［21］和 Trosseille试验［22］对比验证有效性，除了 Nahum试验仿真得到的前额压力略高之外，其它响应都与试验数据基本吻合［47－48］。

1.9 TUST(Tianjin University of Science and Technology)模型

2006年，芦俊鹏和何培基于中国人CT数据分别构建了第50百分位TUST颅脑有限元模型，如图9所示，模型共计33 726个节点，40 861个单元，该模型的仿真结果通过与 Nahum尸体试验［19］对比，验证了模型的有效性，随后并进行了颅脑的正碰与侧碰的生物力学响应分析［51－52］。

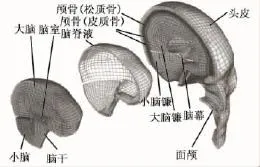
图8 湖南大学HBM(Human Body Model)头部模型［47－48］Fig.8 Hunan University head model of human body［47－48］

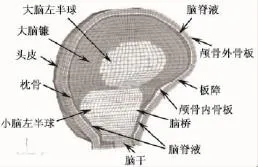
图9 天津科技大学面颅模型［51－52］Fig.9 TUST cacial cranium model［51－52］

2007年，李霞等基于中国人 CT数据构建了TUST面颅有限元模型［53－54］，如图 10 所示，该模型包括1 916个节点，1 552个单元，并且基于Nahum的面骨创伤试验［55］验证了有效性。

图10 天津科技大学颅脑模型［53－54］Fig.10 TUST craniocerebral model［53－54］

2009年，裴永生等基于上述 TUST模型进行改进，构建了新型的头部有限元模型，如图11所示，模型包括颅骨、面骨、大脑、小脑、脑干和大脑镰，单元类型为20节点二阶六面体单元，总共46 919个单元，53 436个节点，并进行头部的正面撞击与侧面撞击研究［49］。

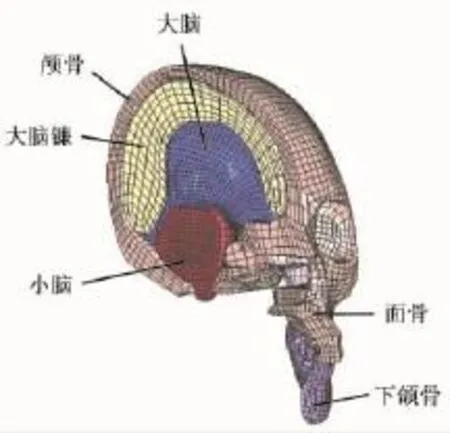
图11 天津科技大学头部有限元模型［49］Fig.11 TUST head finite element model［49］

上述近代头部有限元模型总结如表1和表2所示。

2 展望

尽管有限元模型经过十几年的发展已经取得了一定的进展，但是至今仍没有完善的有限元模型用来重构人体头部的撞击。

根据已有的科研成果和实际工程需要，本课题未来的研究趋向将有以下几个方面

1)我国头部有限元的生物力学仿真尚处于起步阶段，研究中所应用的几何模型大多是从欧美人种的数据中得到的，其尺寸是否适合中国人尺寸分布需要科学论证。

表1 近代有限元模型的数据来源、结构、材料属性、边界条件及验证方法Tab.1 Data source，structures，material properties，boundary conditions and validation methods of modern finite element models

表2 模型应用及其局限性与不足Tab.2 Applications，limitations and shortcomings of modern finite element models

2)现有的头部有限元模型基本都是基于国外第50百分位的人体解剖学数据构建而成，而且若想研究其它百分位头部的响应，还需要通过缩放的方法得到［50］，其科学性和可靠性需要通过构建真实尺寸的模型进行验证。

3)先前有限元模型的面部结构基本都是被简化的，若要提高模型的生物逼真度，则还需要在面部结构上进行改进。

4)进一步完善模型的结构，优化模型网格质量。

5)为了得到更精确的结果，在构建头部模型之后，需继续构建相应百分位的颈部有限元模型。

6)进一步探讨组织材料的各向异性、不均匀性、非线性。

7)进行更多的动物试验和尸体试验来为有限元模型提供能够验证有效性的数据，以及研究其损伤机理，确定其损伤阈值。

通过这些改进，具有更高生物逼真度的有限元模型的仿真准确度将大幅度提高，通过改变模型材料参数、边界条件及在不同部位施加不同类型载荷，可用来模拟不同受力状态下各个组织的动力学响应过程，从而取代其它昂贵试验。

［1］芦俊鹏.颅脑有限元模型的构建和锤碰撞颅脑左侧的计算模拟及分析［D］.天津:天津科技大学，2006.

［2］裴永生.人体头部损伤生物力学建模及其碰撞分析［D］.天津:天津科技大学，2009.

［3］Ishikawa R，Kato K，Kubo M.Finite element analysis and experimental study on mechanism of brain injury using brain model［C］//Dhawan AP.Annual International Conference of the IEEE Engine. New York:Institute ofElectricaland Electronics Engineers，2006:1327－1330.

［4］Takahashi T，Kato K，Ishikawa R.3-D finite element analysis and experimental study on brain injury mechanism［C］//Dittmar A. AnnualInternationalConference ofthe IEEE Engineering in Medicine and Biology Society.Lyon:Institute of Electrical and Electronics Engineers，2007:3613－3616.

［5］Miyazaki Y，Tachiya H，Anata K.Measurement of pressure responses in a physical model of a human head with high shape fidelity based on CT/MRI data［J］.International Journal of Modern Physics B，2008，22(9):1718－1723.

［6］Denny-Brown D，Russell WR.Experimental cerebral concussion［J］.Journal of Physiology，1940，53(1):153 －224.

［7］Denny-Brown D. Cerebralconcussion ［J］. Physiological Reviews，1945，25(2):296－325.

［8］Foda MA，Marmarou A.A new animal model of diffuse brain injury in rats.Part II.Morphological characterization ［J］.Journal of Neurosurgery，1944，80(2):301－313.

［9］Marmarou A，Shima K.Comparative studies of edema produced by fluid percussion injury with lateral and central modes of injury in cats［J］.Advances in Neurology，1990，52:233－300.

［10］Gennarelli TA，Adams JH，Graham DI.Acceleration induced head injury in the monkey.I.The model，its mechanical and physiological correlates［J］.Acta Neuropathologica，1981，7:23－25.

［11］Ommaya AK，Hirsch AE，Flamm ES.Cerebral concussion in the monkey:an experimental model［J］.Science，1966，153(732):211－212.

［12］Ommaya AK. Scaling ofexperimentaldata on cerebral concussion in sub-human primates to concussion threshold for man［C］//Proceedings of 11thStapp Car Crash Conference.Anaheim:Society of Automotive Engineers，1967:73－80.

［13］Ommaya AK， FischFJ， MahoneRM etal.Comparative tolerances for cerebral concussion by head impact and whiplash injury in primates［C］//InternationalAutomobile Safety Conference.Brussels:Society of Automotive Engineers，1970:808－817.

［14］Ommaya AK， Corrao P，Letcher FS.Head injury in the chimpanzee.Part 1:Biodynamics of traumatic unconsciousness［J］.Journal of Neurosurgery，1973，39:167 －177.

［15］Hodgson VR，Thomas LM，Khalil TB.The role of impact location in reversible cerebral concussion［C］//Proceedings of 27thStapp Car Crash Conference.Pennsylvania:Society of Automotive Engineers，1983:225 －240.

［16］Gennarelli TA，Thibault LE，Adams J et al.Diffuse axonal injury and traumatic coma in the primate ［J］.Annals of Neurology，1982，12:564－574.

［17］Gennarelli TA， ThibaultLE， TomeiG etal. Directional dependence of axonal brain injury due to centroidal and noncentroidal acceleration［C］//Proceedings of 31stStapp Car Crash Conference. New Orleans:Society ofAutomotive Engineers，1987:49 －53.

［18］Ono K，Kikuchi A，Nakamura M.Human head tolerance to sagittal impact reliable estimation deduced from experimental head injury using sub-human primates and human cadaver skulls［C］//Proceedings of 24thStapp CarCrash Conference.Pennsylvania:Society of Automotive Engineers，1980:101－160.

［19］Nahum AM，Smith R，Ward CC.Intracranial pressure dynamics during head impact［C］.//Proceedings of 21stStapp Car Crash Conference.Pennsylvania:Society of Automotive Engineers，1977:339－366.

［20］Trosseille X，Tarriére C，Lavaste F.Development of a F.E.M.of the human head according to a specific test protocol［C］//Proceedings the 36thCar Crash Conference.Seattle:Society of Automotive Engineers，1992:235– 253.

［21］Yoganandan N. Biomechanics ofskullfracture ［C］//International symposium on head injury research.Washington D C:Society of Automotive Engineers，1994:659 －668.

［22］Hardy WN，Foster CD，Mason MJ.Investigation of head injury mechanisms using neutral density technology and high-Speed biplanar X-ray［J］.Stapp Car Crash Journal，2001，45:337 －368.

［23］Hardy CH，Marcal PV.Elastic analysis of a skull［R］.0671437，1971.

［24］Ward CC，Thompson RB.The development of a detailed finite element brain model［C］//Proceedings of 19thStapp Car Crash Conference.Pennsylvania:Society of Automotive Engineers，1975:641－674.

［25］Shugar TA，Katona MC.Development of finite element head injury model［J］. JournalofAmerican Society ofCivil Engineering，1975，101:233－239.

［26］Hosey RR，Liu YK.A homeomorphic finite element model of impact head and neck injury［C］//Proceedings of International Conferenceon FiniteElementsin Biomechanics. Tucson:Applied Science Publishers，1980:851 －870.

［27］Dimasi F，Marcus J，Eppinger R.3D anatomic brain model for relating cortical strains to automobile crash loading［C］//Proceedingsofthe International TechnicalConference on Experimental Safety Vehicles.Washington:National Highway Traffic Safety Administration，1991:916－923.

［28］Gennarelli AT，Thibault EL.Acceleration damage to the brain［C］//Proceedingsofthe Advisory Group forAerospace Research and Development. New York:ElsevierScience Publishers，1982:1－9.

［29］Mendis K.Finite element modeling of the brain to establish diffuse axonal injury criteria［D］.Ohio:Ohio State University，1992.

［30］Ward CC.Finite element models of the head and their use in brain injury research［C］//Proceedings of 26thStapp Car Crash Conference.AnnArbor:SocietyofAutomotiveEngineers，1982:71－85.

［31］Khalil TB，Viano DC.Critical issues in finite element modeling of head impact［C］//Proceedings of 26thStapp Car Crash Conference.AnnArbor:SocietyofAutomotiveEngineers，1982:87－102.

［32］Sauren AAHJ，Claessens MHA.Finite element head modeling of head impact:the second decade［C］//Proceedings of the international IRCOBI conference on the biomechanics of impact.Eindhoven:International Research Council on the Biomechanics of Injury，1993:241－251.

［33］Ruan JS，Khalil TB，King AI.Dynamic response of the human head by impact by three-dimensional finite element analysis［J］.Journal of Biomechanical Engineering，1994，116:44 －50.

［34］Ruan JS，Li Haiyan，Wang Xuekui.A new exploration of the applicability of the head injury criterion［J］.Chinese Journal of Biomedical Engineering，2007，24(6):1373－1377.

［35］Zhou Chun，Khalil TB，King AI.A new model comparing impact responses of the homogeneous and inhomogeneous human brain［C］//Proceedings of 39thStapp Car Crash Conference.Pennsylvania:Society of Automotive Engineers，1995:121－137.

［36］Zhang Liying， YangKH， DwarampudiR.etal.Recent advances in brain injury research:a new human head model development and validation［C］//Proceedings of 45thStapp Car Crash Conference. San Antonio:Society of Automotive Engineers，2001:375－400.

［37］Dokko Y，Anderson RWG，Zhang Liying.Validation of the human head FE model against pedestrian accidents and its tentative application to the examination of the existing tolerance curve［C］//18thInternational Technical Conference on the Enhanced Safety of Vehicles.Nagoya:National Highway Traffic Safety Administration，2003:NO.322.

［38］Willinger R，Kang HS，Diaw B.Three-dimensional human head finite-element model validation against two experimental impacts［J］.Annals of Biomedical Engineering，1999，27(3):403 －410.

［39］Kang HS，Willinger R，Diaw BM.Validation of a 3d anatomic human head model and replication of head impact in motorcycle accident by finite element modeling［C］//Proceedings of 41stStapp Car Crash Conference.Lake Buena Vista:Society of Automotive Engineers，1997:329 －338.

［40］Claessens MHA.Finite element modeling of the human head under impact conditions［D］.Eindhoven:Eindhoven University of Technology，1997.

［41］Brands DWA，Bovendeerd PHM.On the potential importance of non-linear viscoelastic material modelling for numerical prediction of brain tissue response:test and application［J］.Stapp Car Crash Journal，2002，46:103－121.

［42］Kleiven S，Hardy WN.Correlation of an FE model of the Human Head with Experiments on Localized Motion of the Brain-Consequences for Injury Prediction［C］//Proceedings of 46thStapp Car Crash Conference. Ponte Vedra:Society of Automotive Engineers，2002:123 －144.

［43］Mendis KK， StalnakerRL， AdvaniSH. A constitutive relationship for large deformation finite element modelling of brain tissue［J］.Journal of Biomechanical Engineering，1995，117(3):279－285.

［44］Kleiven S，Von Holst H.Consequences of head size following trauma to the human head［J］.Journal of Biomechanics，2002，35(2):153－160.

［45］Horgan TJ，Gilchrist MD.The creation of three-dimensional finite element models for simulating head impact biomechanics［J］.International Journal of Crashworthiness，2003，8(4):353－366.

［46］Horgan TJ，Gilchrist MD.Influence of FE model variability in predicting brain motion and intracranial pressure changes in head impact simulations ［J］. International Journal of Crashworthiness，2004，9(4):401－418.

［47］许伟，杨济匡.研究颅脑交通伤的有限元模型的建立及验证［J］.生物医学工程学杂志，2008，25(3):557－561.

［48］许伟，杨济匡.用于交通伤评估的头部有限元模型的虚拟试验验证［J］.汽车工程，2008，30(2):151－155.

［49］裴永生.人体头部损伤生物力学建模及其碰撞分析［D］.天津:天津科技大学，2009.

［50］Meijer R，Wisgerhof R.Scaling head-neck response data and derivation of 5thpercentile female side-impact dummy head-neck response requirements in NBDL test conditions ［J］.International Journal of Crashworthiness，2009，14(3):233 －243.

［51］芦俊鹏.颅脑有限元模型的构建和锤碰撞颅脑左侧的计算机模拟及分析［D］.天津:天津科技大学，2006.

［52］何培.三维人体颅脑有限元模型和颅脑正面碰撞分析［D］.天津:天津科技大学，2006.

［53］李霞，阮世捷，李海岩.人体面骨三维有限元模型重构及碰撞分析［J］.微计算机信息，2007，34(23):277－278.

［54］李霞.基于有限元法的人体头部损伤的研究［D］.天津:天津科技大学，2007.

［55］Nahum AM. The prediction of maxillofacialtrauma ［J］.American Academy of Ophthalmology and Otolaryngology.1976，84(5):932－933.