疑似脑死患者脑电信号的动态近似熵分析

杨 琨 曹建庭，2，3* 王如彬 朱惠莉

1(华东理工大学认知神经动力学研究所，上海 200237)

2(日本埼玉工业大学大学院工学研究科，日本埼玉县深谷市 396-0293)

3(日本理化研究所脑科学研究中心.日本埼玉县和光市 351-0198)

4(华东医院呼吸科，上海 200040)

引言

脑死亡，是指人的全脑和脑干功能完全的、不可逆转的丧失。脑死亡是人生命的终结，所以对脑死亡判定的研究具有重要的意义。在1968年的第22届世界医学大会上，美国哈佛医学院脑死亡定义审查特别委员会提出，将“脑功能完全不可逆地丧失”作为新的死亡标准，并制定了世界上第一个脑死亡判定标准:“1.深度昏迷;2.自主呼吸停止;3.脑干反射消失;4.脑电消失或平坦(2 μV以下)”［1－2］。尽管不同国家对脑死亡的判定标准略有不同，如日本的判定标准除了上述4项外还增加了瞳孔散大的项目，但是一些基本的判定项目是一致的［3］。

现有的脑死判定程序比较耗时，而且存在一定的风险。例如，在实施“有无自主呼吸”的检查时，需要拔去患者的呼吸器，由此而导致患者死亡的例子也曾经发生过［4］。还有，“确认平坦脑电”的检查一般至少需要12 h，个别也有超过200 h才能确认的。在此，引入一种更为简单有效的方法，即利用脑电预测系统对患者进行脑死亡预判定。在预判定过程中，对还具有脑电节律的患者可中止判定程序并返回对其进行治疗，对未提取出脑电节律的患者仍可以按现有的脑死判定程序进行判定。引入脑电预测系统的最大优点在于可避免脑死亡的误判，并且能减轻医生和患者的负担［5－6］。

复杂度是用来衡量时间序列随机性程度的一个指标。如果一个序列的复杂度高，那么这个序列的随机程度也较高。常见的复杂度指标包括伦伯尔－齐夫定义的 CLZ复杂度、近似熵(approximate entropy，ApEn)、C0复杂度等。作为一个随机性复杂度，近似熵描述的是一个时间序列在模式上的自相似程度，被应用于分析睡眠脑电等研究中。例如，对正常人睁眼、闭眼、浅睡、深睡等4种状态脑电的近似熵研究显示，人在深睡时没有意识，大脑的活动相对不是很“复杂”，其复杂度很低;而在清醒时，大脑接收大量外界的信息，其近似熵比闭眼时的要大［7－9］。

在对疑似脑死患者进行脑死亡判定的研究中，首先对所有患者的脑电信号进行独立成分分析(ICA)［5］，把其结果与医生通过临床诊断患者的结果进行对照，发现无论从数据分析的角度还是从临床判定的角度，对脑死者的判定结果是一致的。虽然独立成分分析具有较强的去噪和成分提取的功能，但对于未提取到脑电节律的部分患者的判定缺乏严谨，所以又引入能量指标［10］和复杂度指标，对疑似脑死患者的脑电信号进行分析。在复杂度方面，首先运用了近似熵(ApEn 法)、C0复杂度［11－12］、NSSE 法［13］、DFA 法［14－15］4 种不同的复杂度，对采集到的部分患者的脑电数据进行处理，经过概率验证(P值验证等)后，从宏观上得出了昏迷患者和脑死亡者的两类脑电确实具有特征差异的结论［6］。随着采集的脑电数据量的增加，对所有35例患者、共计61次脑电数据进行近似熵分析，进一步确认和衡量脑死者和昏迷患者脑电随机性程度的差异［16］。

通过对所有被测脑电信号的静态近似熵的分析，虽然从宏观上得到了昏迷患者与脑死者两类脑电信号的差异，但是在微观方面，静态近似熵值仅是一个值，不能实时反映疑似脑死患者状态的变化。本研究引入动态近似熵，从而在微观方面能反映脑电信号的近似熵变化，也能观察到疑似脑死患者生命体征的变化。引入动态近似熵分析法后，发现个别疑似脑死患者脑电信号的分析结果和期望值有一定偏差，其原因在于抢救室里各种仪器设备对脑电记录存在干扰。为减弱噪声的影响，引入小波分析法先对脑电信号进行去噪前处理，然后再进行动态近似熵分析。

1 动态近似熵

静态近似熵分析法被用于反映一个时间序列在模式上的自相似程度，即当维数变化时序列中产生新模式的可能性大小。ApEn越大，产生新模式的机会越大，因而序列越复杂［8］。静态近似熵分析只是对其中的某段数据求值，不能反映整个测量时间段近似熵的变化过程。在此，引入一个时间变量t，对现有的静态近似熵分析法在时间轴上进行扩展，从而得到动态近似熵。

对于一个时间长度为T的时间序列s(t)，定义其动态近似熵为 ApEn(m，r，t)，其中 m为矢量维数，r为阈值，即选定的相似容限，t为时间。引入一个宽度为t′的时间窗口，窗口沿着时间轴 t不断移动，进入窗口的时间序列可表示为

式中:t=0，…，T－t′;N为时间窗口对应的序列长度，见图1。

在序列 Xt中，按照顺序构造两个 m维矢量Vt(i)和 vt(j)，则有

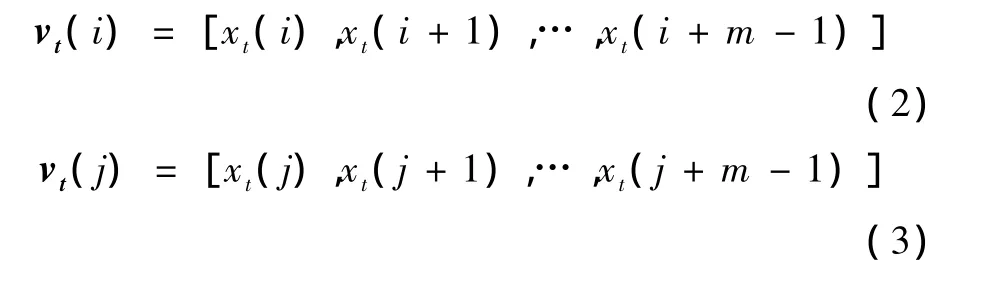
式中，i，j≤N － m+1。

D［vt(i)，vt(j)］表示矢量 vt(i)和 vt(j)之间的距离，则有

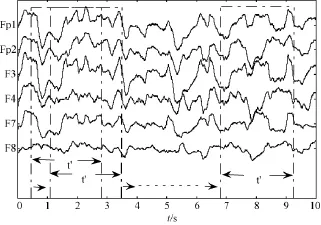
图1 动态近似熵的窗口移动Fig.1 The diagram of dynamic ApEn

对于给定阈值 r及矢量 vt(i)，当 j≤N－m+1时，计算出与vt(i)的距离小于r的矢量vt(j)个数，则Cm

i(r，t)表示对于所有 j≤N－m+1时的矢量，vt(j)与vt(i)距离小于r的概率，有

对于每个 m+1，重复上述步骤，得到 φm+1(r，t)，则动态近似熵为

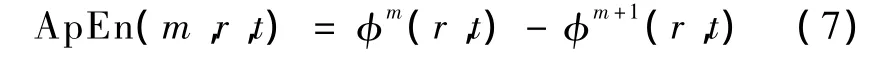
在一般情况下，时间序列取100～5 000点即可，m=2，r取时间序列标准差的 0.1 ～0.2 倍［7－8］。由于近似熵是把随机性作为对复杂型的度量，即衡量一个时间序列的随机性程度，因此对于随机序列和正弦波来说，正弦波的随机性要小于随机序列。具体到疑似脑死患者脑电信号的分析中，由于昏迷患者还有脑活动，测得的脑电信号是具有一定周期性的脑电节律与噪声的叠加，其近似熵较小;而脑死者的脑电信号是各种干扰源产生的噪声总和，其近似熵应该较大。根据这个原理，可以利用近似熵分析法来识别是否脑死。

2 小波分析

采用小波分析法对信号去噪，其本质在于小波变换对信号和噪声的瞬时特性表现不一样。本研究所使用的脑电数据是从重症监护室中获得的，采集到的脑电受到外部各种干扰源的影响。对于一个含噪声e(t)的原始信号f(t)，其基本模型可以表示为

式中，e(t)为噪声，σ称为噪声强度。

在最简单的情况下，可以假设e(t)为高斯白噪声，且 σ=1。小波法去噪的目的，就是要抑制e(t)以恢复s(t)。

2.1 小波变换

小波变换的基本思想是用一簇函数表示或逼近待分析信号或函数。这一簇函数被称为小波函数系，是由基小波或母小波的函数通过平移和伸缩而构成的一组正交基［17－18］。将待分析信号在小波函数系上做分解，即可得到一维连续小波变换，有

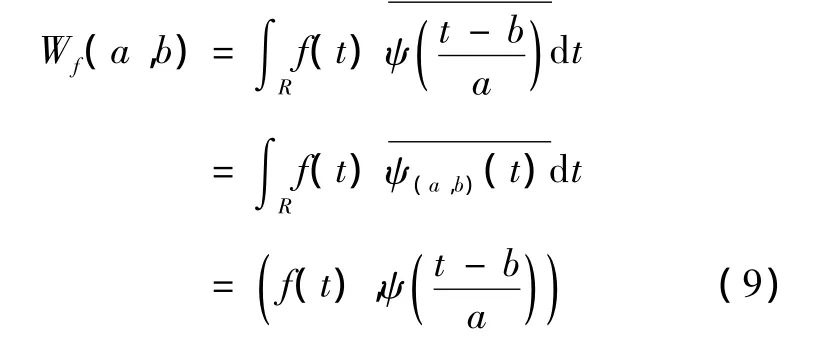
式中:a，b∈R，R为实数域，a被称为伸缩因子(又称尺度因子)且 a≠0，b为平移因子;ψ(a，b)(t)表示由基小波生成的小波函数系表示小波函数系的共轭。Wf(a，b)为待分析信号f(t)在固定小波函数ψ(a，b)(t)上的分量，表达了 f(t)与该小波函数的相似程度。

在实际应用中，为了方便计算机处理，尺度因子和平移因子需要进行离散化处理，则离散的小波变换可表示为

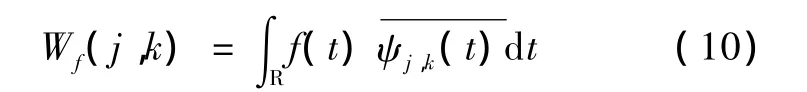
式中:j，k是将 a，b离散化后的参数，R为实数域，ψj，k(t)为离散小波函数，时间t仍为连续变量。

2.2 小波去噪方法

利用小波变化进行去噪的方法有很多，本研究利用阈值法去噪，即对含噪信号f(t)作离散小波变换，所得到的小波系数一部分是与信号对应的小波系数，另一部分是与噪声对应的小波系数，具有不同的统计特性，通常信号的系数值要大于噪声的系数值。需要找到一个合适的阈值λ，将绝对值小于阈值的小波系数舍弃，将绝对值大于阈值的小波系数保留或收缩，得到小波系数的估计值;根据这个估计值进行信号重构，从而得到去噪后的信号［19－20］。

3 患者脑电数据采集和分析计算流程

研究所用到的脑电数据全部是从医院的重症监护室里测得的，所使用的脑电仪是便携式NEUROSCAN ESI-32系统。在这个系统中，一共有7个电极被放在昏迷患者的前额，分别是 Fp1，Fp2，F3，F4，F7，F8 和地极，A1，A2 作为参考电极放在耳朵上，见图2。脑电信号的采样频率是1 000 Hz，电极阻抗低于8 000 Ω［5］。

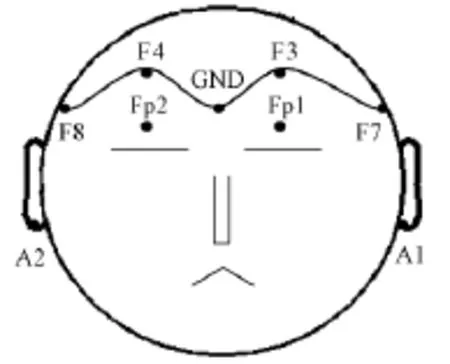
图2 电极安放系统［14］Fig.2 The electrode layout［14］

在2004年6月 ～2006年3月期间，共采集了35名患者的脑电信号。这些患者包括19名昏迷患者和16名脑死者，年龄从17～85岁不等。根据这些患者的健康状况，记录了不同的脑电数据。图3是两例疑似脑死患者的脑电信号。

加入小波前处理的动态近似熵算法流程如下，其中N为时间窗口 t＇对应的序列长度，r为阈值，维数m初值为2，nt为时间窗口的起始点，wname为选择的小波函数，lev为小波分解层数。

步骤1:读取脑电信号 data，设置初值 N，r，m，nt，wname，lev。

步骤2:由 wname，lev，对脑电信号 data采用小波分析法去噪，得到去噪后的信号datalb。

步骤3:从datalb中提取起始值为nt，长度为N的时间序列datnew。

步骤4:给定初值 i=1，sum=0。

步骤 5:由 i，得到 xi=datnew(i:i－ m+1)。

步骤6:由每个不大于N－m+1的j值得到xj=datnew(j:j－m+1)，计算出 D(xi，xj)≤r的个数 n，c=n/(N － m+1)，sum=sum+logc。

步骤 7:i=i+1，若 i≤N － m+1，重复步骤 5、6，直到 i>N －m+1，则 φm=sum/(N －m+1)。

步骤8:m=m+1时，重复步骤4～步骤7，得到φm+1，则 apen=φm－φm+1。

步骤9:移动窗口，使 nt=nt+N，重复步骤3～步骤8，得到一系列apen，并作图。

4 数据分析结果

4.1 昏迷患者和脑死者的动态近似熵分析

图3 脑电预测系统所测的疑似脑死患者的脑电信号。(a)患者A的脑电信号;(b)患者B的脑电信号Fig.3 The EEG recordings of two patients.(a)the EEG recording of patient A;(b)the EEG recording of patient B

对所测得的35例患者、共计61次脑电信号进行动态近似熵分析，发现一部分脑电信号的近似熵较小，在0附近较小的范围内变化，如图4(a)所示的患者A动态近似熵的分析结果;另一部分脑电信号的近似熵值较大，在1附近较小的范围内变化，如图4(b)所示的患者B动态近似熵的分析结果。根据近似熵的定义，较小的近似熵值说明脑电信号中存在周期性的脑电节律，即患者还有脑活动，处于昏迷状态;而较大的近似熵值说明脑电信号中存在随机性的噪声，患者可能为脑死者。将这些数据分析的结果同医生对患者病状的诊断进行对照，发现用动态近似熵分析法的结果和医生的判定是一致的。

图4 利用动态近似熵对患者的脑电信号进行分析的结果。(a)对患者A的脑电信号的分析结果;(b)对患者B的脑电信号的分析结果Fig.4 Dynamic ApEn results for two patients.(a)Dynamic ApEn results for patient A;(b)Dynamic ApEn results for patient B

采集的脑电信号还包括了一例体征状态改变(即由昏迷变为脑死状态)患者的脑电信号。2005年10月18日，患者意识不明、瞳孔散大，但有微弱的对光反射，处于深昏迷状态;10月19日，患者状况恶化，各种脑干反射均消失，被医生判定为脑死亡。在患者昏迷状态以及被判定为脑死状态时，对其的脑电信号进行了多次测量，利用文中第1节提出的动态近似熵进行分析，得到如图5所示的结果。图5左侧的近似熵值较小，在整个过程中，总在0附近较小的范围内变化;而图5右侧的近似熵值较大，大部分时间都在1附近较小的范围内变化。根据近似熵的定义，图5左侧的脑电信号存在周期性脑电节律，患者处在昏迷状态。而图5右侧的脑电信号存在随机噪声，患者可能处于脑死状态。可见，笔者对数据分析的结果同医生的临床判定结论是一致的。包括上述结果，35个病例中的31个病例只需利用开发的动态复杂度便可得到类似的识别结果。

4.2 与小波分析结合的动态近似熵分析

虽然从图4和图5中可以看出，不管是处于不同状态的不同患者，还是体征状态改变的同一患者，处于昏迷状态时的近似熵总是在0附近的较小范围内变化，而处于脑死状态时的近似熵则在1附近的较小范围内变化。但是，在图5中，脑死状态的脑电信号在300 s处的动态近似熵忽然降低，和左侧昏迷状态的动态近似熵相差不大。如果仅对300 s前后的这段脑电信号进行传统的动态近似熵分析，对患者状态的判定会出现失误。为了避免误判，在对所测的脑电信号实施动态近似熵分析之前，使用小波分析法去除由测量环境中仪器设备产生的高频周期噪声。图6是采用小波分析法滤波后，昏迷患者A和脑死亡者B的动态近似熵比较。对比图4和图6可以看出，噪声干扰较小时，对脑电信号的动态近似熵的分析结果影响不大。

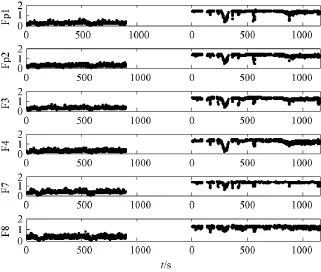
图5 利用动态近似熵对患者C的脑电信号进行分析的结果Fig.5 Dynamic ApEn results for patient C

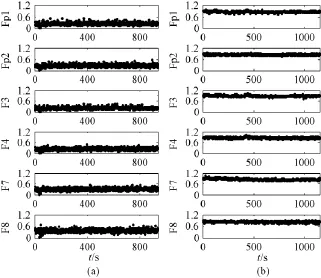
图6 利用小波分析法和动态近似熵对患者的脑电信号进行分析的结果。(a)利用小波分析法和动态近似熵对患者A的脑电信号的分析结果;(b)利用小波分析法和动态近似熵对患者B的脑电信号的分析结果Fig.6 Dynamic ApEn with a wavelet denosing technique for two patients.(a)Dynamic ApEn with a wavelet denosing technique for patient A;(b)Dynamic ApEn with a wavelet denosing technique for patient B

用小波法去噪后，对昏迷变为脑死状态的患者脑电信号进行动态近似熵比较，见图7。对比图5和图7，在300 s处，采用小波分析法去噪后，高频周期噪声的影响降低，脑死状态脑电信号的近似熵总在1附近变化。包括上述结果在内，35个病例中的4个病例在利用小波分析与动态近似熵结合的方法后，其识别效果更好。因此，在进行动态近似熵分析之前，对测得的数据进行小波去噪前处理是非常必要的。

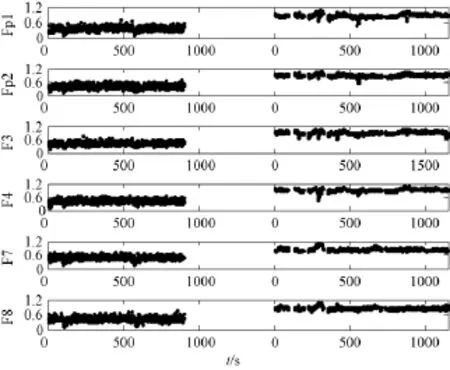
图7 利用小波分析法和动态近似熵对患者C的脑电信号进行分析的结果Fig.7 Dynamic ApEn with a wavelet denosing technique for patient C

为了进一步分析图5中患者的脑死状态脑电信号在第300 s前后的噪声成分，对导联Fp1上这段长约103 s的信号采用小波分析法去噪，滤除的噪声如图8(a)所示;对噪声进行傅里叶变换，得出其频谱图，如图8(b)所示。从图8(b)中可以看出，被滤除的噪声带有很强的150 Hz的成分，而这一成分的干扰主要是来自外部设备的电源干扰。

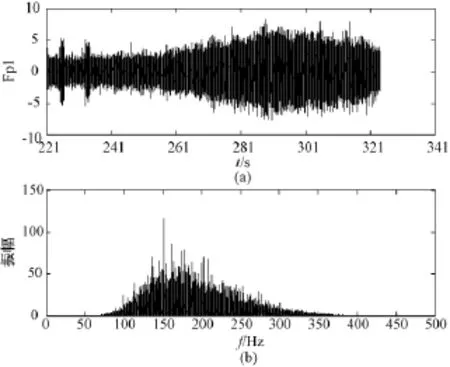
图8 患者C在脑死状态300s前后滤除的噪声。(a)滤除的噪声;(b)对噪声进行傅立叶变换的结果Fig.8 The interfering noise in patient C’s EEG data around the 300th second.(a)the interfering noise;(b)Fourier transformation of the interfering noise

5 结论

在本研究中，首先在静态近似熵分析法中引入时间参量，并把它扩展成动态近似熵分析法，用来识别昏迷患者与脑死者的脑电信号，以及观察患者病状的变化过程。由于脑电信号中存在由仪器设备产生的高频周期噪声，所以首先采用小波分析法对脑电信号进行去噪前处理，然后再对去噪后的脑电信号进行动态近似熵分析。在整个测量和分析过程中，昏迷患者的近似熵小于脑死者的近似熵，昏迷患者的近似熵在接近于0的很小范围内变化，而脑死者的近似熵则在1附近的很小范围内变化。共对35例患者进行了数据分析和识别，得出的结论与医生的临床判定是完全一致的。今后的研究重点是高噪声下脑死亡数据的分析与识别。

［1］Ad hoc committee of the Harvard medical school to examine the definition of brain death.A definition of irreversible coma［J］.JAMA，1968，205(6):337－340.

［2］陈忠华.脑死亡:现代死亡学［M］.北京:科学出版社，2004.

［3］Wijdicks EFM.Brain death worldwide:accepted fact but no global consensus in diagnostic criteria ［J］.Neurology，2002，58:20－25.

［4］Marks SJ，Zisfein J.Apneic oxygenation in apnea tests for brain death:a controlled trial［J］.Archives of Neurology，1990，47(10):1066－1068.

［5］Cao Jianting.Analysis of the quasi-brain-death EEG data based on a robust ICA approach ［J］.Lecture Notes in Computer Science，2006，10:1240－1247.

［6］Cao Jianting，Chen Zhe.Advanced EEG signal processing in brain death diagnosis［M］//Signal Processing Techniques for Knowledge Extraction and Information Fusion.Berlin:Springer，2008:275－298.

［7］Pincus SM.Approximate entropy(ApEn)as a measure of system complexity［J］.Proc Natl Acad Sci USA，1991，88:110－117.

［8］顾凡及，梁培基.神经信息处理［M］.北京:北京工业大学出版社，2007.

［9］张泾周，马颖颖，李婷，等.基于复杂性测度的睡眠脑电分期处理方法研究［J］.中国生物医学工程学报，2009，28(3):367－371.

［10］Shi Qiwei，Yang Juhong，Cao Jianting，et al.EMD based power spectral pattern analysis forquasi-brain-death EEG ［J］.Emerging Intelligent Computing Technology and Applications.With Aspects of Artificial Intelligence，2009，5755:814－823.

［11］Gu Fanji，Meng Xin，Shen Enhua，et al.Can we measure consciousness with EEG complexities?［J］International Journal of Bifurcation and Chaos，2003，13:733－742.

［12］Chen Fang，Xu Jinghua，Gu Fanji，et al.Dynamic process of information transmission complexity in human brains［J］.Biol Cybern，2000，83:355－366.

［13］RobertsSJ， Penny W， Rezek L. Temporaland spatial complexity measures for EEG-based brain-computer interfacing［J］.Medical and Biological Engineering and Computing，1998，37(1):93－99.

［14］Peng CK，Buldyrev SV，Havlin S，et al.Mosaic organization of DNA nucleotides［J］.Phys Rev E，1994，49:1685 －1689.

［15］Little M，McSharry P，Moroz I，et al.Nonlinear，biophysicallyinformed speech pathology detection［C］//Proceedings of ICASSP’06.New York:IEEE Publishers，2006:1080 －1083.

［16］Yang Kun，Shi Qiwei，Cao Jianting，et al.Analyzing EEG of quasi-brain-death based on approximate entropy measures［C］// Advances in Cognitive Neurodynomics. Berlin:Springer，2009(in press)

［17］徐晨，赵瑞珍，干小兵.小波分析·应用算法［M］.北京:科学出版社，2004.

［18］高志，余啸海.Matlab小波分析工具箱原理与应用［M］.北京:国防工业出版社，2004.

［19］吴镇扬.数字信号处理的原理与实现［M］.南京:东南大学出版社，2001.

［20］张翀，余红英.基于小波分析的心电信号降噪研究［J］.山西大学学报(自然科学版)，2008，31(S2):57 －62.