典型藏式古建木构梁柱连接转动性能试验研究

杨 娜，闫会春，2

（1．北京交通大学 土木建筑工程学院，北京100044；2．北京金港机场建设有限责任公司，北京100071）

藏式古建筑的历史意义、宗教意义、艺术价值一直是世人关注的热点。不少藏式建筑建造年代久远，其内部结构已经存在大量的残损现象，进行结构性能的评估以采取合理保护措施显得尤为重要。与汉式古建筑相比，藏式古建筑在结构构造上具有鲜明的特色，通过构件间的垂直叠压实现节点连接功能，并辅以暗销来定位，并不采用复杂的榫卯和斗拱。已有的汉式古建筑的研究成果不能直接应用于藏式古建筑，因此开展针对藏式古建木构的结构性能研究必要且急迫。

当前对于古建木结构的研究，主要着眼于汉式木结构整体及节点连接的静动力性能［1－3］，简化结构计算模型［3］。通过试验研究［5－6］等对典型构件进行性能分析，特 别 地 对 榫 卯［7－8］、斗 拱［9－11］的 动 力 特 性及其耗能减震机理作了较为丰富且深入的研究。已有的研究成果对汉式古建木构节点连接的力学行为的解释和描述，为古建筑的加固维修和保护提供了依据。与此同时，对于藏式古建筑的研究一直集中在建筑风格、装饰艺术及宗教意义方面。拉萨古艺建筑美术研究所阿旺罗丹等［12］对藏式建筑的类型进行了概括，从结构组成、建筑材料、装饰艺术及施工工艺等多个角度对藏式建筑的特点进行了详细探讨。陈耀东［13］从历史、文化的角度详细阐述了藏族建筑体系的形成和发展，全面讨论了藏式建筑文化和建筑技术成就。以上研究对建筑材料、空间布局、类别及细部构造等进行了总结，少数从受力的角度对结构残损状况、破坏原因等进行了分析，但缺乏对梁、柱、连接等典型构件的结构静、动力性能分析。

该文针对典型藏式古建木构梁柱连接进行结构静力分析，通过静力试验提取了弯矩－转角曲线模型，分析了相关因素对节点初始转动刚度的影响规律，反复荷载作用下刚度退化规律，并对组成节点的各构件进行了宏观受力状态分析。

1 试验概况

试验选取在藏式古建筑中普遍应用的梁柱连接节点作为研究对象。该类节点从下往上依次由柱、斗、垫木、弓木、梁构成，各构件垂直叠压，采用暗销连接，梁端结合处采用燕尾榫增强联系，构造见图1所示。

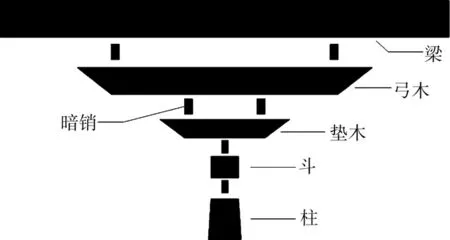
图1 节点构造

1．1 试件设计

对于藏式建筑而言，建筑模数没有定式，节点各构件的截面和长度通常随房间变化，但垫木的尺寸通常变化不大。试验中仅考虑当梁的截面和跨度确定时，弓木长度、暗销位置对于节点转动刚度的影响，设计6个试件进行静力试验，试件编号及参数变化见表1。

表1 试件编号及参数变化

不考虑柱身的扭转及弯曲，试件无柱，以SJ1为标准试件，其尺寸见表2，各试件暗销布置见图2。

图2 各试件暗销布置

表2 SJ1各构件尺寸

1．2 材性试验

藏式古建筑木构体系用材主要是藏青杨，维修时替换木材主要为松木，试验试件采用樟子松加工。试验所用木材的材性试验在中国林业科学研究院木工所力学实验室进行，取样数量和尺寸按中国标准《木材物理力学性能实验方法》执行。

材性试验主要进行了5个指标的测试，包括：含水率、气干密度、顺纹抗压强度、顺纹抗拉强度、抗弯弹性模量。其余材性指标参照文献［14］规定进行推导获得。

按照文献［14］的推荐原则，对材性试验结果进行处理，获得试验木材各项性能如表3所示。表3中X、Y、Z代表木材L（纵向）、R（径向）、T（弦向）3个方向。将材性试验的结果与文献［14］的结果进行对比可知，试验所用木材为典型樟子松。

1．3 试验装置及加载制度

藏式古建筑属密梁平顶式结构，其构架示意图如图3所示。楼盖系统由椽子、占棍及楼面组成，楼面采用传统的阿嘎土夯制而成，密度较大，且椽子与梁连接紧密，因此楼盖系统对梁的转动有一定的约束作用。同时上下层柱对齐，传递竖向集中力，经过现场实测［12］某典型藏式古建筑中柱顶传递的集中力为60～100 k N。

表3 樟子松材性参数

图3 藏式建筑构架组成

选取下层节点分析其荷载及约束情况：1）不考虑柱身的扭转和弯曲变形，不设置柱子，同时不考虑结构平面外变形，则斗底为固定约束；2）梁在柱顶是不连续的，为分析一侧梁与柱的相对转动能力，固定非加载梁，并认为其在加载过程中转动很小；3）分析及试验中不设置楼盖系统，即忽略了上层柱础与梁间的柔性约束作用，故上层柱集中力取较小值60 k N。简化过程见图4。

图4 试验模型荷载及约束简化过程

试验中设置一钢板压在梁间榫卯相连处，用于模拟柱础，同时也可体现楼盖系统对梁转动的约束作用，通过数值模拟计算知，当板长超过500 mm后，约束作用基本保持不变，故试验中采用长约600 mm，厚度为20 mm，宽度为150 mm的板。实际结构中，2梁连接处竖向位移很小，故试验中设置千斤顶既能模拟柱间传递的集中力，又能保证梁连接处的竖向位移。

按上述荷载及约束简化，试验装置如图5所示。加载装置为一固定于实验室反力架的手动液压千斤顶（千斤顶1），其最大压荷载为300 k N；非加载梁端部固定，斗底固定；梁间榫卯相连处采用千斤顶2压一钢板，试验过程中先施加千斤顶2，出力大小固定在60 kN。

图5 试验装置

试验加载（千斤顶1出力）分为预加载和正式加载2个阶段，加载制度见图6。

其中Ti，1为第i次加载初始时刻，Ti，2为第i次加载结束时刻，T i，3为第i次卸载初始时刻，Ti，4为第i次卸载结束时刻，Ti，2与Ti，3间隔表示加载至破坏荷载后持续时间，试验中为10 min；T i，4与T i＋1，1间隔表示第i次卸载完成后持时时间，试验中为10 min。各试件加载制度如表4所示，表中i表示首次加载，j表示最后一次加载。

图6 加载制度

试验中屈服状态和极限状态的界定：由于节点并无明显屈服点，随相对转角加大，其承受弯矩也逐渐增大，因此，定义在梁柱相对转角明显加大而弯矩增长较为平缓时为屈服状态；节点的构造特点决定了梁梁榫卯间可发生滑移和转动，直到脱卯才会导致破坏，此时为极限状态。实际试验中，由于上部钢板约束作用，不可能发生脱卯，故极限状态定义为梁端位移过大，持续卸载，无法继续施加荷载，同时斗发生劈裂破坏。为考察试件在卸载之后的回弹能力，试验中对部分试件进行了多次加卸载。

表4 各试件加载制度

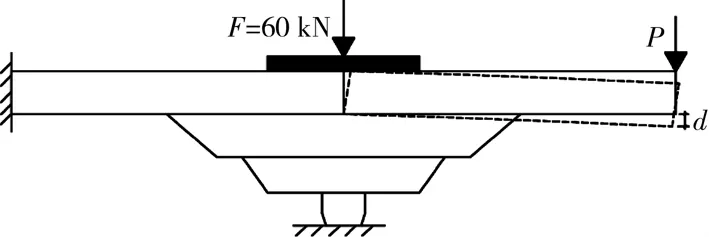
图7 梁端位移

1．4 测试内容及测点布置

为分析节点的转动性能需要测量的物理量为：施加的荷载、加载点位移、梁端连接处的转动情况、弓木及梁的受弯情况。应变片用于考察截面的应变发展情况，位移计、倾角计用于测量节点的位移。6个试件的测点布置完全相同，图8为SJ1的测点布置示意图，其中S表示应变片，括号内为前后对称布置的应变片，共12个；G表示倾角计，共1个；D表示位移计，共1个。

图8 SJ1测点布置

2 典型试验过程及现象

加载制度如1．3节所述，Ti，1—Ti＋1，1为典型试验过程。其余阶段的过程、现象都与此相同。试验过程及现象描述如表5所示。试验现象见图9。

表5 典型试验过程与现象

图9 试验现象图片

3 试验结果及分析

3．1 节点弯矩－转角曲线

试验中试件的荷载及约束简化示意图如图10所示。假定加载过程中梁、弓木及垫木的相对转动一致，不考虑非加载梁的转动，可用梁端部截面AB的转角θ来代替梁柱相对转角，对应的弯矩为M＝PL。根据试验采集的数据，可获得每个试件的节点弯矩－转角曲线，如图11所示。图中Ki表示节点的初始转动刚度（弹性阶段刚度），Kp表示塑性刚度，θy表示节点达到屈服状态（定义见1．3节）的转角，θu表示节点达到极限状态（定义见1．3节）的转角。根据Origin曲线拟合可以得到以上4个参数的试验结果，如表6、表7所示。其中，Ki求解一般舍弃前2个采集量，原因在于由木材干缩及试件加工造成榫卯连接非常紧，初始加载时主要克服各个连接件间的摩擦，在稍微松动后，采集到的转角值才能反映出节点自身的转动性能。

图10 荷载及约束简化

图11 节点弯矩－转角曲线

由试验结果可知：各试件的弯矩－转角曲线都表现出较强的双线性曲线性质，节点的弯矩－转角曲线模型可用双线性模型表示（图12），其表达式如下：

其中，Ki、Kp、θy、θu与弓木长度、暗销位置等因素有关。

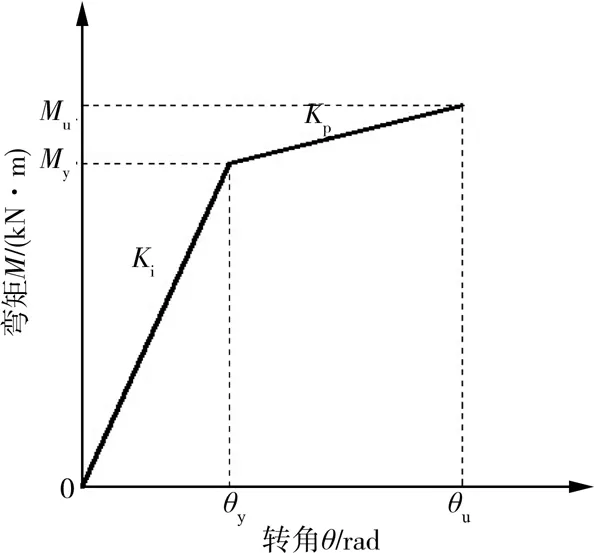
图12 节点转动模型

表6 试验结果统计

表7 各试件刚度值

3．2 弓木长度的影响

SJ1、SJ2、SJ3的区别在于改变了弓木长度，弓木与梁长之比分别为0．7、0．8、0．9。根据试验结果（表6、表7）可以得出弓木长度对于节点转动性能的影响。

由表6、7可知，随弓木长度加大，节点初始转动刚度增大，极限承载力增大，位移角延性系数稍变小，在2．34～2．80之间，节点的塑性转角θy、θu保持一致，塑性转角可取为0．045 rad，极限转角可取为0．118 rad（均值）。3个试件的初始转动刚度关系如图13所示，随弓木长度的增大，节点初始转动刚度几乎呈线性增大趋势，且塑性刚度均为初始刚度的1／3左右。综上可知，弓木长度的增加能够有效提高节点抗转动的能力，提高节点转动刚度，但对节点的延性几乎无影响。

3．3 暗销位置的影响

SJ4、SJ5、SJ6与SJ1相比改变了暗销的位置，将它们的试验结果进行比较，可得到暗销位置对于节点转动性能的影响。

图13 弓木长度的影响

比较SJ1、SJ4、SJ5的试验结果，可以得到弓木－梁暗销位置内移对于节点转动性能的影响。由图14可知，弓木－梁间暗销内移后，节点的初始转动刚度下降，且内移距离越多下降越大。由表6可知，SJ4、SJ5的承载能力显著下降，但延性系数提高，均为4．0。

比较SJ1、SJ6结果可知，垫木－弓木间暗销内移后，节点的初始转动刚度下降。结合SJ4结果，暗销内移距离都是100 mm的情况下，垫木－弓木间暗销引起的节点初始刚度下降更大。但SJ6的承载能力及塑性转角等都有所增加。

图14 暗销位置的影响

3．4 刚度退化

考虑木结构的恢复能力，在试验过程中，除SJ1之外，其余试件均采用多次加载，考察节点在反复荷载作用下的刚度退化规律，及残余变形的累积过程。以SJ3为例进行分析，SJ3以梁端位移d（图7所示）作为控制量，共进行了7次加卸载。试验结果统计如表8所示。

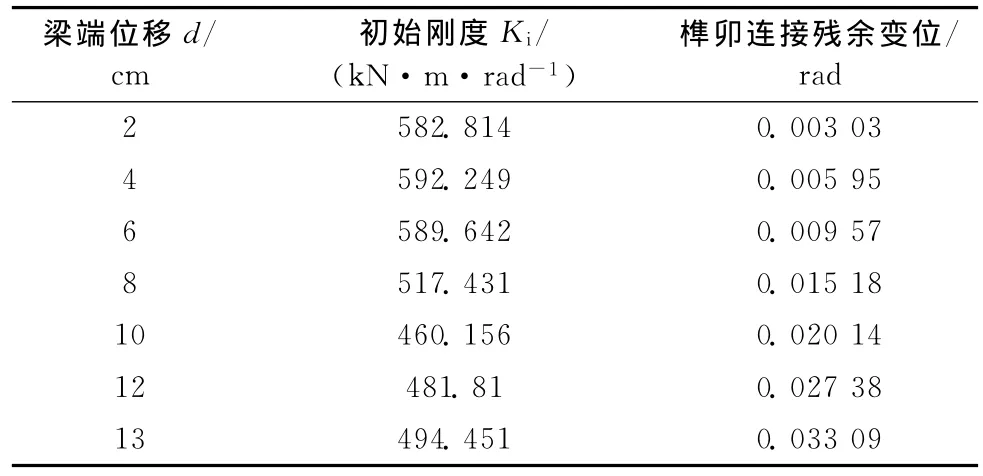
表8 SJ3各次加卸载刚度值及残余变位

结果表明梁端位移d对节点初始转动刚度及残余变位有很大影响，随d加大，初始刚度退化（图15）。d≤6 cm时，初始刚度值趋于稳定，可取为588．235 k N·m／rad（均值）；d≥10 cm后，初始刚度值趋于稳定，可取为478．806 k N·m／rad（均值），即d＝6 cm是初始转动刚度发生明显退化的转折点。

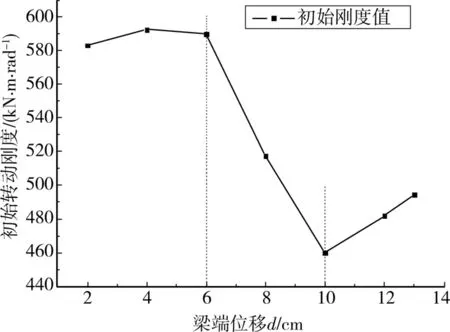
图15 初始转动刚度退化

随梁端位移加大，每次卸载后榫卯连接处的残余转角逐渐加大。d＜6 cm时，残余转角很小，整个结构表现出良好的变形能力及回弹能力，d≥6 cm后，残余转角明显增大，整个结构塑性变形增大（图16）。

图16 残余转角累积

分析上述结果可知，在反复荷载作用下，随塑性变形发展，节点初始转动刚度退化，并有明显的跃迁现象。当荷载值小于临界荷载P1（如d＝6 cm）时，结构处在弹性变形阶段，卸载后几乎无塑性变形，节点的初始转动刚度几乎无退化；当荷载值大于临界荷载P1（如d＝6 cm）时，结构塑性变形迅速增加，节点初始转动刚度退化明显；荷载继续增加至临界荷载P2（如d＝10 cm）后，塑性变形已充分发展，节点初始转动刚度值退化不明显，甚至有稍微反弹现象。

3．5 节点区各构件受力状态

如前所述，在试验过程中，梁、弓木、垫木表现出明显的受弯形态，且均为上侧受拉下侧受压。在加载过程中，垫木与斗接触位置发生压入现象，斗在接触部位为横纹承压，这是整个节点区塑性变形的主要来源。通过对拆卸后构件观察发现，暗销存在较明显的剪切变形，主要承受剪力作用。

总结节点区各个构件的受力状态如表9所示。在试验中，屈服状态和极限状态的界定以梁柱间转角为依据（定义见1．3节），除斗发生了劈裂破坏外，其余试件基本都处在弹性受力阶段。

表9 节点区各构件受力状态

4 结论

选取典型藏式古建筑节点作为结构原型，改变弓木长度、暗销位置进行了6个试件的静力试验研究，得到典型藏式古建筑梁柱节点的转动性能相关结论如下：

1）节点的弯矩－转角曲线可采用双线性模型表示。

2）随弓木长度加大，节点初始转动刚度增大，极限承载力也变大。

3）暗销内移会影响节点的转动能力，弓木－梁间暗销内移后，节点转动刚度变小；垫木－弓木间暗销内移后，节点转动刚度变小；相同条件下，弓木－梁间暗销内移对于节点转动刚度的影响小于垫木－弓木间暗销内移带来的影响。

4）在反复荷载作用下，随塑性变形发展，节点初始转动刚度退化，并有明显的跃迁现象。在临界荷载P1之前，刚度退化不明显，超过此荷载值，刚度有较大退化，达到临界荷载P2后，刚度退化不明显，甚至有稍微反弹现象。

5）组成节点的各构件受力状态为：梁、弓木、垫木受弯，均为上侧受拉下侧受压；斗为横纹承压构件，产生较大塑性变形；暗销起抗剪作用。

［1］徐其文，汤小平，索安勇．中国古典建筑木结构特性的分析研究［J］．淮海工学院学报，2002，11（4）：64－67．XU QI－WEN，TANG XIAO－PING，SUO AN－YONG．A study on the structural characteristics of ancient chinesetimber architectures［J］．Journal of Huaihai Institute of Technology，2002，11（4）：64－67．

［2］仓盛，竺润祥，任茶仙，等．榫卯连接的古木结构动力分析［J］．宁波大学学报：理工版，2004，17（3）：332－335．CANG SHENG，ZHU RUN－XIANG，REN CHAXIAN，et al．Dynamic analysis of ancient wood structures with mortise and tenon connection［J］．Journal of Ningbo University：Natural Science ＆Engineering Edition，2004，17（3）：332－335．

［3］KING W S，YEN J Y，YEN Y N．Joint characteristics of traditional Chinese wooden frames［J］．Engrg．Struct．1996，18（8）：635－644．

［4］BULLEIT W M，SANDBERG L B，DREWEKM W，et al．Behavior and modeling of wood－pegged timber frames［J］．Struct．Engrg．，ASCE，1999，125（1）：3－9．

［5］方东平，俞茂宏，宫本裕，等．木结构古建筑结构特性的实验研究［J］．工程力学，2000，17（2）：75－83．FANG DONG－PING，YU MAO－HONG，MIYAMOTO Y， et al． Experimental studies on structural characteristics of ancient timber architectures［J］．Engineering Mechanics，2000，17（2）：75－83．

［6］高大峰，赵鸿铁，薛建阳．中国木结构古建筑的结构及其抗震性能研究［M］．北京：科学出版社，2009．

［7］SEO J M，CHOI I K，LEE J R．Static and cyclic behavior of wooden frames with tension joints under lateral load［J］．Struct．Engrg．ASEC，1999，125（3）：344－349．

［8］SANDBERG L B，BULLEIT W M，REID E H．Strength and stiffness of oak pegs in traditional timber－frame joints［J］．Struct．Engrg．，ASCE．2000，126（6）：717－723．

［9］津和佑子，藤田香织，金惠园．传统木结构建筑构件的动力荷载试验（第一部分）微动测定与自由振动试验［C］／／日本建筑学会．日本建筑学会大会学术讲演论文集．2004：23－24．

［10］金惠园，藤田香织，津和佑子．传统木结构建筑构件的动力荷载试验 （第二部分）荷载变形关系与变形特征［C］／／日本建筑学会．日本建筑学会大会学术讲演论文集．2004：25－26．

［11］藤田香织，金惠园，津和佑子．传统木结构建筑构件的动力荷载试验（第三部分）恢复力特性与刚度的讨论［C］／／日本建筑学会．日本建筑学会大会学术讲演论文集．2004，：27－28．

［12］阿旺罗丹．西藏藏式建筑总揽［M］．成都：四川美术出版社，2007．

［13］陈耀东．中国藏族建筑［M］．北京：中国建筑工业出版社，2007．

［14］木结构设计手册编辑委员会．木结构设计手册［M］．3版．北京：中国建筑工业出版社，2005．