渗透水压下岩体多裂纹相互作用的计算

杨 慧，江学良，曹 平

（1．中南林业科技大学 土木工程与力学学院，长沙410004；2．湖南城市学院 土木工程学院，湖南 益阳 413000；3．中南大学 资源与安全工程学院，长沙410083）

地下岩体常以多裂纹的面貌出现，由于裂纹尖端应力分布的奇异性，容易引发裂纹尖端材料局部失效而导致宏观破坏，岩石断裂力学的研究主要集中在对均质材料中特殊单一裂纹或者规律性分布裂纹断裂力学行为的探讨，进而对复杂多裂纹岩体的力学行为进行研究。多裂纹相互作用分析，作为岩体材料细观破损分析的关健问题，近几十年来获得了广泛的关注，发展了多种分析方法［1－10］。基于应力叠加技术，Kachanov提出了一种计算多裂纹相互作用下应力强度因子的简单方法，并进一步用来估算多裂纹体等效弹性 参 数 及 分 析 裂 纹 体 的 应 力、应 变 场［6－7］。Li等［10］，李银平［11］，H．Qing［12］等对 Kachanov法提出了改进，提高了计算精度。Basista［8］、李银平［13］等将该方法推广到压缩荷载下准脆性物体中多个压剪裂纹相互作用的问题。实际工程中的岩体赋存于一定的地应力和地下水压力环境中，地下水与岩体相互作用。处于渗透压下的多裂隙岩体，其力学行为将发生改变。地应力在裂隙面的法向分量一半使结构面受到压缩并使深埋岩体中的裂隙闭合，而地下水压力作用于裂隙面的法向，力图使裂隙面张开。无渗透水压时裂纹尖端的应力为压应力，在渗透水压下可能转化为拉应力，裂纹尖端的复杂应力状态直接影响着裂纹尖端的应力强度因子值。关于渗透压下的岩桥贯通规律，学者已作了一些理论及试验研究［14－16］，但对于应力场和渗透压共同作用下岩体中多裂纹相互作用的研究甚少。

本文根据断裂力学理论，建立无限大板含多裂纹的力学模型，根据叠加原理，推导远场应力和裂隙水压力共同作用下的多裂纹应力强度因子，并在此基础上研究渗透水压下多裂纹的相互作用，为渗透压条件下的多裂隙岩体断裂失稳的研究提供初步理论依据。

1 水－岩力学作用下多裂纹应力强度因子计算

考虑裂隙渗透水压的情况如图1所示，无限平面x－o－y内 含 有N条 裂 纹，裂 纹 长 度 为2ai（i＝1，…，N），与x轴的夹角为αi（i＝1，…，N），受远场双轴压应力σ∞＝－（σ1∞，σ3∞），裂隙水渗透压力为pw，垂直于裂纹表面。

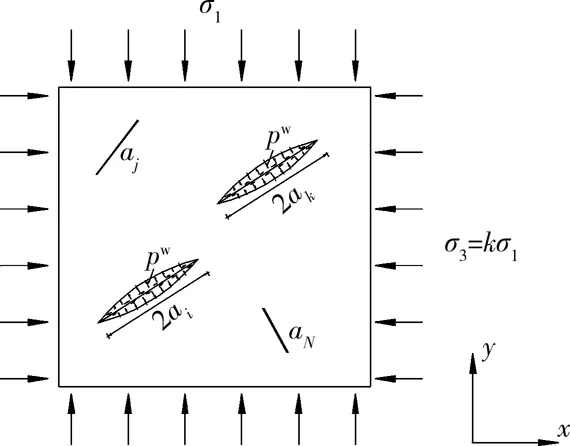
图1 渗透水压下多裂纹计算模型

对任意裂纹i，根据任意斜面上应力分量变换关系，可知作用于裂纹面上的法向及切向应力分别为［16］

1）裂纹未闭合情况：

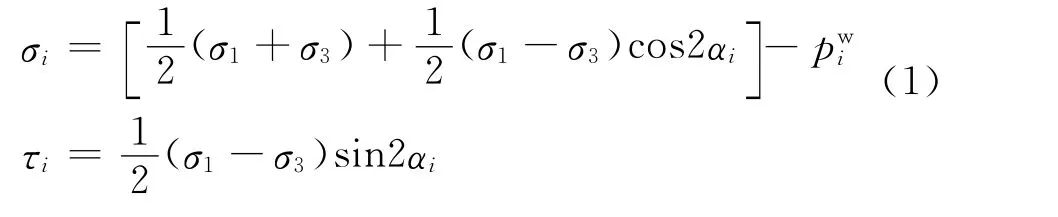
2）裂纹闭合情况：

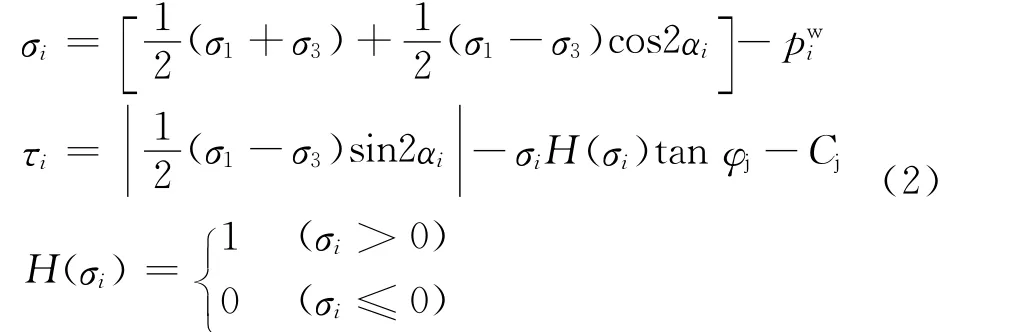
其中，tanφj为摩擦系数，Cj为内聚力。

将此问题分解为N个子问题，每个子问题中只含有一条裂纹，而无穷远处应力为零，每条裂纹面上受法向及切向应力作用，是初始面力和由于其他N－1条裂纹的存在而引起的附加面力两者之和。如图2所示，例如：第k裂纹面上所受的法向及切向应力为p k（sk）和qk（sk）。该问题又可以分解为N个子问题，每个子问题中只有一条单裂纹，且裂纹表面应力情况未知，例如：单独考虑第k裂纹，其裂纹面上的应力为Pk（sk）和Qk（sk）。

图2 多裂纹叠加示意图

根据叠加原理，得到Fredholm积分方程［5］

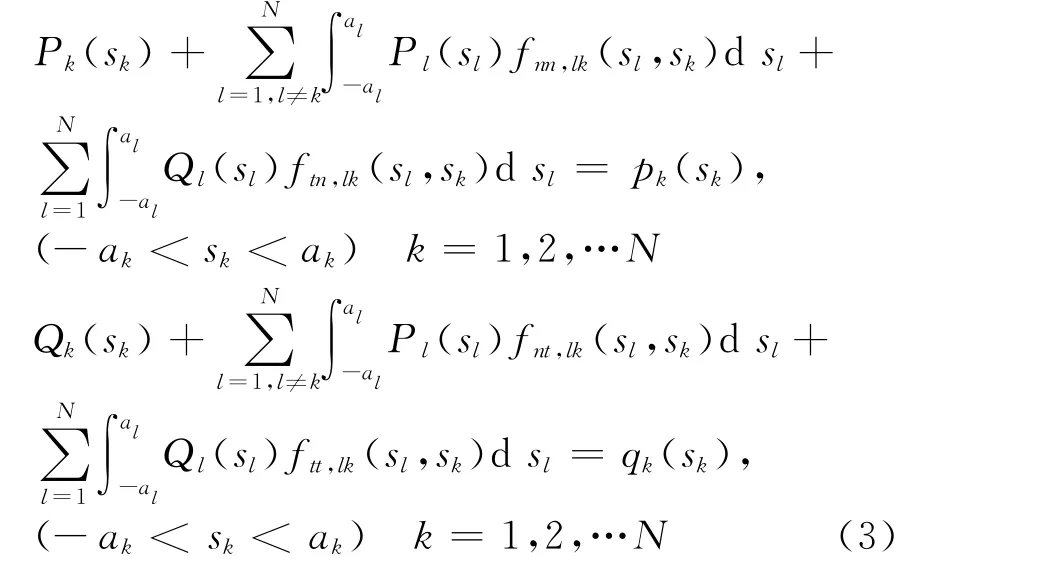
式中，f nn，f nt，f tn，f tt为相互作用系数，表达式见附录A。假设Fredholm积分方程在离散点M处能获得满意的计算结果，则由式（3）即可得到N条裂纹的2×N×M个方程，再利用Chebyshev数值迭代规则即可得到

通过分析，将边界条件带入式（1）、（2），即可以通过MATLAB编程计算得出Pk，Qk，从而由下式得到水－岩力学作用下各裂纹尖端的应力强度因子

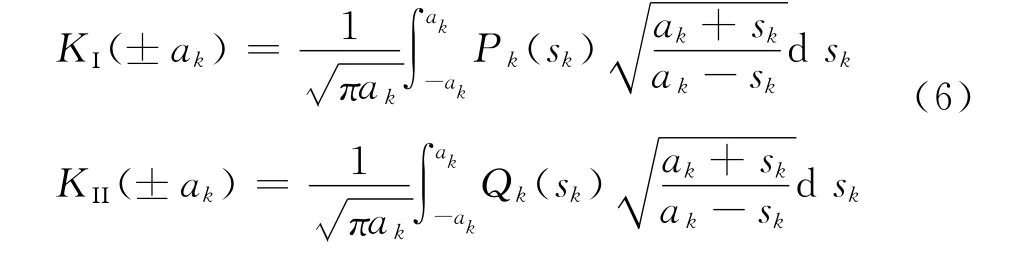
2 算例分析

2．1 2条裂纹算例分析

无限板中含2条裂纹，取2a＝20 mm，裂纹之间垂直距离2d＝2 mm，平行距离2b＝4 mm，取σ1＝10 MPa，σ3＝4 MPa，裂隙水压力p＝2 MPa，如图3所示。

图3 2条裂纹计算模型

根据式（3）得到各裂纹的相关方程并代入式（4）得

求解以上方程组即可求得2条裂纹相互影响下的P1（si），Q1（si），P2（ti），Q2（ti），代入式（6），计算得到不同裂纹倾角下裂纹尖端各点的应力强度因子值。如果不考虑裂纹之间的相互影响，根据断裂力学理论，将式（1）代入下式，即可得到任一裂尖端应力强度因子为

将虑裂纹间相互影响计算得到的结果与上式进行对比，得到无量纲应力强度因子值，见图4。

图4 2条裂纹F1A，F1B…，F2D值

2．2 3条裂纹算例分析

无限板中含3条裂纹，取2a＝20 mm，①②裂纹间2b＝10 mm，①③裂纹间2d＝4 mm，取σ1＝10 MPa，σ3＝4 MPa，裂隙水压力p＝2 MPa，如图5所示。根据式（3）得到各裂纹的相关方程并代入式（4）得

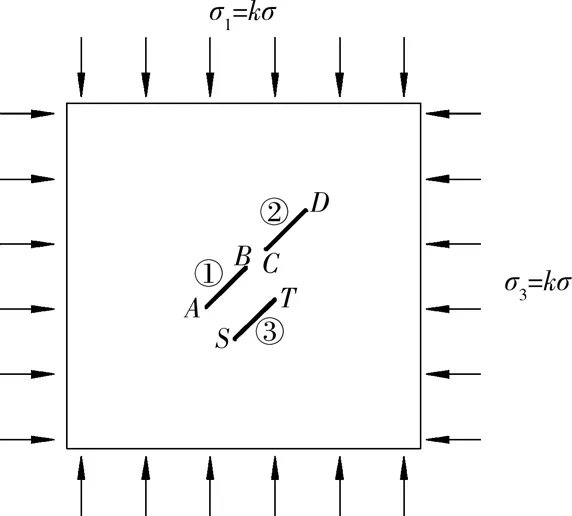
图5 3条裂纹计算模型

求解以上方程组即可求得3条裂纹相互影响下的P1（si），Q1（si），P2（ti），Q2（ti），P3（ki），Q3（ki），代入式（6），计算得到不同裂纹倾角下裂纹尖端各点的应力强度因子值。将虑裂纹间相互影响计算得到的结果与式（9）进行对比，得到无量纲应力强度因子值，见图6。

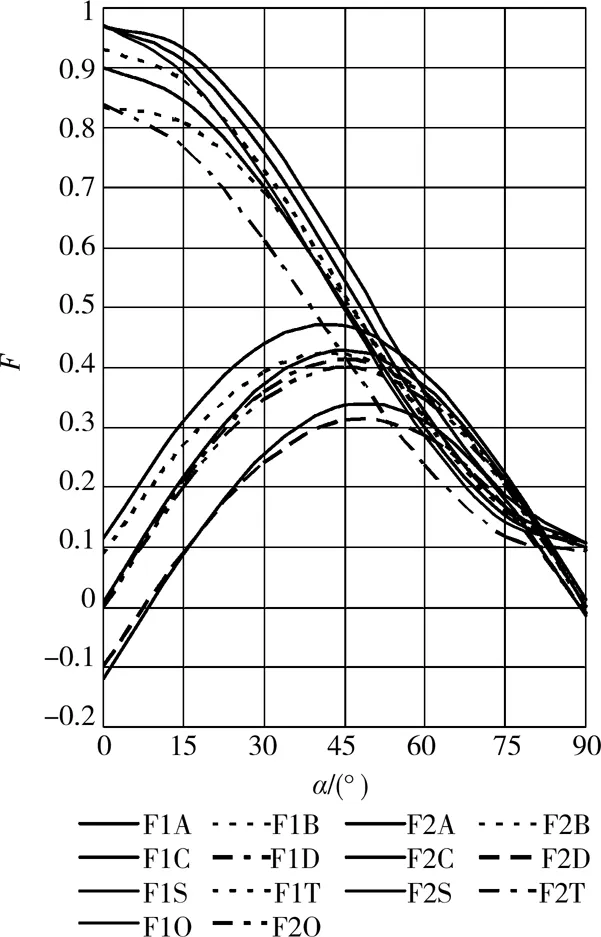
图6 3条裂纹F1A，F1B…，F2T值

图中F各值如下式：

由图4、图6可知，多裂纹的相互作用对裂纹尖端处的应力场影响较大，根据裂纹的相对几何位置和裂纹倾角变化，进行不同叠加后的应力场可产生2种效应，应力强度影响加强区与应力强度影响减弱区，当相邻裂纹尖端处于加强区时，该裂纹的应力强度因子将会变大，反之则变小。

3 渗透压下多裂纹相互作用分析

计算模型见图3，按裂纹渗透水压p＝0、2、4、6、8、10 MPa；裂纹间垂直距离2d＝2 mm，水平距离2b＝0、2、4、6、8、10 mm共36种情况进行计算，得出了各种情况下裂纹尖端的应力强度因子，如图7—8所示。

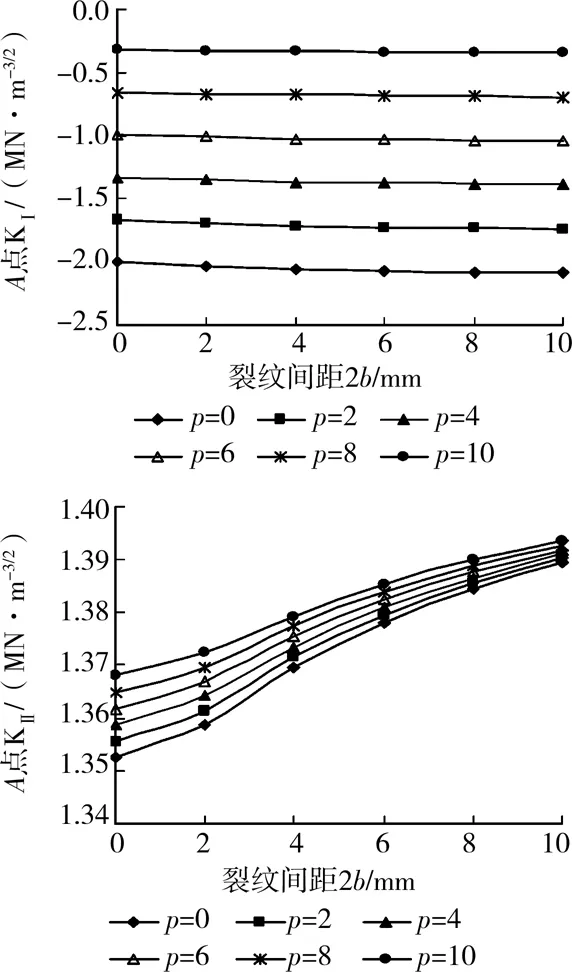
图7 裂纹1尖端A点KI、KII值

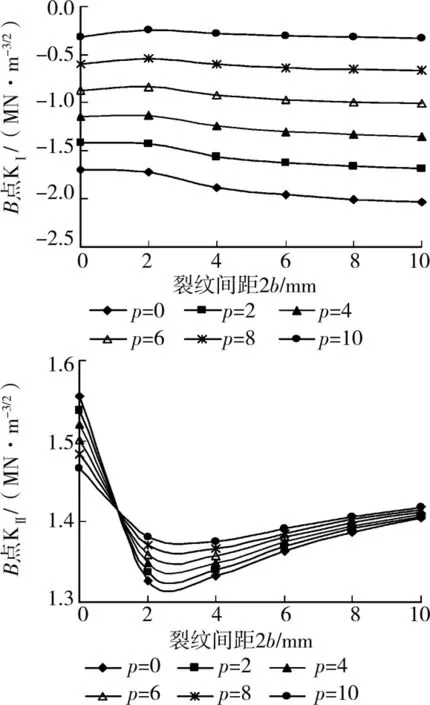
图8 裂纹1尖端B点K I、K II值

从上图可知，各条裂纹尖端KI随着渗透压的增大而增加，即使－KI逐渐减小，这说明裂隙水压力抵消了一部分正应力。裂纹外端部A点的KII有相同的变化趋势，而内端部B点KII的变化还受到相邻裂纹尖端应力场的影响，随着裂纹水平间距的增大出现先减小后增大的规律，但最终都趋于一个定值，该值为考虑单一裂纹计算所得到的KII。

对于闭合裂纹，其端部I型应力强度因子恒为零，由裂纹上下表面间摩擦力的存在影响了裂纹面的相对滑动，从而影响应力强度因子KII，见图9。从图中可知，2条裂纹尖端的应力强度因子变化趋势相同，都随摩擦系数的增大而减小。

图9 摩擦系数对K II的影响

4 结 论

1）岩体中的裂隙大都成组出现，每一个裂纹都被其他裂隙所包围，这些都会影响裂纹尖端附近的应力状态。多裂纹的相互作用对裂纹尖端处的应力场影响较大，根据裂纹的相对几何位置和裂纹倾角变化，进行不同叠加后的应力场可产生2种效应，应力强度影响加强区与应力强度影响减弱区，当相邻裂纹尖端处于加强区时，该裂纹的应力强度因子将会变大，反之则变小。

2）渗透水压的存在，大大的改变了裂隙尖端的应力强度因子，各条裂纹尖端KI随着渗透压的增大而增加（使－KI逐渐减小），这说明裂隙水压力抵消了一部分正应力。

3）不同间距的平行裂纹相互影响所产生的应力强度因子的变化趋势是完全一致的，且随着裂纹间距离的加大，计算所得出的应力强度因子值都趋于一个定值，该值为没有裂纹影响时的应力强度因子值。考虑裂纹间的相互作用与裂纹间的相对距离有关，当裂纹间距＞裂纹长度时，可以忽略裂纹相互作用对裂纹尖端应力场的影响。

［1］CHEN Y Z．Multiple crack problems of antiplane elasticity in infinite body［J］．Engineering Fracture Mechanics，1984（20）：767－775．

［2］CHEN Y Z．Solutions of multiple crack problems of a circular plate or an infinite plate containing a circular hole by using Fredholm integral equation approach［J］．International Journal of Fracture，1984（25）：155－168．

［3］LAM K Y，PHUA S P．Multiple crack interaction and its effect on stress intensity factor［J］．Engineering Fracture Mechanics，1991（40）：585－591．

［4］CHEN Y Z．A survey of new integral equations in plane elasticity crack problem ［J］． Engineering Fracture Mechanics，1995（51）：97－134．

［5］MARK KACHANOV．A simple technique of stress analysis in elastic solids with many cracks［J］．International Journal of Fracture，1985（28）：R11－R19．

［6］MARK KACHANOV．Elastic solids with many cracks：a simple method of analysis［J］．International Journal of Solids and Structure，1987（23）：23－43．

［7］LARISSA GORBATIKH， MARK KACHANOV． A simple technique for constructing the full stress and displacement fields in elastic plates with multiple cracks［J］．Engineering Fracture Mechanics，2000（66）：51－63．

［8］BASISTA M，GROSS D．A note on crack interactions under compression ［J］．International Journal of Fracture，2000（102）：L67－L72．

［9］MARK KACHANOV．On the problems of crack interactions and crack coalescence［J］．International Journal of Fracture，2003（120）：537－543．

［10］LI Y P，THAM L G，WANG Y H，et al．A modified Kachanov method for analysis of solids with multiple cracks［J］．Engineering Fracture Mechanics，2003（70）：1115－1129．

［11］李银平，杨春和．近置多裂纹相互作用的渐进分析方法［J］．力学学报，2005，37（5）：600－605．LI YIN－PING， YANG CHUN－HE． Asymptotic analysis of interaction of closely－spaced cracks［J］．Chinese Journal of Theoretical and Applied Mechanics，2005，37（5）：600－605．

［12］QING H，YANG W．Characterization of strongly interacted multiple cracks in an infinite plate［J］．Theoretical and Applied Fracture Mechanics，2006，（46）：209－216．

［13］李银平，王元汉，肖四喜．岩石类材料中压剪裂纹的相互作用分析［J］．岩石力学与工程学报，2003，22（4）：552－555．LI YIN－PING， WANG YUAN－HAN， XIAO SI－XI．Interaction of frictional cracks in rock－like materials［J］．Chinese Journal of Rock Mechanics and Engineering，2003，22（4）：552－555．

［14］赵延林，曹平，林杭，等．渗透压作用下压剪岩石裂纹流变断裂贯通机制及破坏准则探讨［J］．岩土工程学报，2008，30（4）：511－517．ZHAO YAN－LIN，CAO PING，LIN HANG，et al．Rheologic fracture mechanism and failure criterion of rock cracks under compressive－shear load with seepage pressure ［J］．Chinese Journal of Geotechnical Engineering，2008，30（4）：511－517．

［15］赵延林，曹平，文有道，等．渗透压作用下压剪岩石裂纹损伤断裂机制研究［J］．中南大学学报：自然科学版，2008，39（4）：838－845．ZHAO YAN－LIN，CAO PING，WEN YOU－DAO，et al．Damage fracture failure mechanism of compressive－shear rock cracks under seepage pressure［J］．J．Cent．South Univ：Science and Technology，2008，39（4）：838－845．

［16］MUSKHELISHVILI．数学弹性力学的几个基本问题［M］．赵惠元．译．北京：科学出版社，1958．

附录A 裂纹相互作用系数和相互作用因子

如图Al所示，无限大平板内有一条长为2a的裂纹AB，坐标原点取于裂纹中点，x轴与裂纹重合，在裂纹附近考虑一虚拟裂纹CD，与x轴的夹角为α，分析虚拟裂纹CD上任意一点的应力情况。

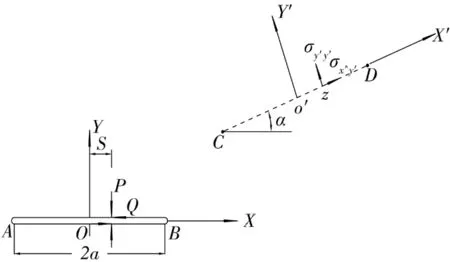
图A1 虚拟裂纹计算

式（3）、式（4）中相互作用系数和相互作用因子可以由弹性力学基本解求得如下［A1，A2］：

参考文献：

［A 1］CHEN Y Z．Multiple crack problems of antiplane elasticity in infinite body［J］．Engineering Fracture Mechanics，1984（20）：767－775．

［A 2］MUSKHELISHVILI．数学弹性力学的几个基本问题［M］．赵惠元．译．北京：科学出版社，1958．