轴向荷载对横向受荷桩承载性状影响的参数分析

梁发云，陈海兵，宋 著

（同济大学a．岩土及地下工程教育部重点试验室；b．同济大学 地下建筑与工程系，上海200092）

在桥梁、高层建筑以及海洋工程中，桩基础通常承受轴向与横向荷载的共同作用。常规桩基设计方法中，一般是将2种受力情况分别计算，然后基于小变形假定直接进行应力叠加［1］。然而，当作用在桩上的轴向荷载较大时，桩的弹性挠曲变形和轴向荷载之间的相互作用影响不容忽视，也即轴向与横向荷载之间产生了明显的耦合效应［2］。对此，横山幸满［3］曾指出：同时承受轴力和水平力作用的桩，严格的来说，应力叠加原理是不适用的。

轴向与横向荷载共同作用下的桩基问题引起了一些学者的关注，多数研究表明［2－5］，轴向荷载对横向受荷桩的作用会使桩身弯矩增加或增大桩的侧向变形，主要区别是对于轴向荷载影响程度的分析结论有所不同。但是也有研究认为轴向荷载对桩基水平承载特性的影响与土性有关［6］或者对桩的侧向变形和内力几乎没有影响［7］。

Zhang等［5］系统地回顾了相关研究文献，指出关于轴向与横向荷载共同作用的试验研究［8－10］多是基于轴向荷载较小的前提下进行的（轴向荷载通常小于桩顶承台的重量），难以清晰地揭示出轴向荷载对横向受荷桩承载性状的影响机理。特别是当桩顶作用的轴向荷载比较大时，如何正确评估轴向荷载对横向受荷桩承载特性的影响非常重要。

本文基于弹性地基梁法，建立轴向与横向荷载作用下的桩基挠曲微分方程，采用有限单元法进行求解，通过参数分析研究轴向荷载对横向受荷桩承载特性的影响，以期为工程设计提供参考。

1 分析方法

对于轴向荷载作用下的横向受荷桩，横向荷载使桩身产生弯矩和挠曲变形的同时，由于桩身挠曲变形的出现，轴向荷载也可能会对桩身的内力和变形产生明显影响，因此，有必要考虑轴向荷载的作用效应。此时桩身的受力情况如图1所示，图中N、H和M分别为作用于桩顶的轴向荷载、横向荷载以及弯矩，p（x，z）为直接作用在桩身上的外荷载，q（x，z）是由外荷载作用产生桩身变形引起桩侧土产生的连续分布的地基反力。

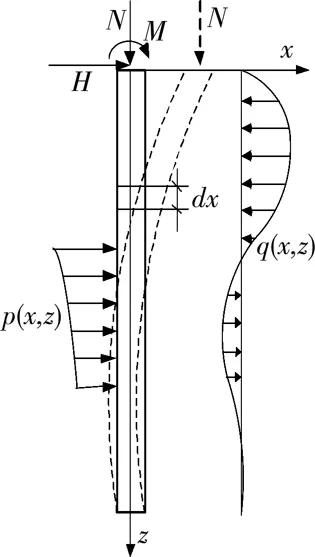
图1 桩身受力示意

将桩视作弹性地基梁，通过桩身微元受力分析，建立轴向与横向荷载共同作用下的桩单元挠曲微分

方程如式（1）。

其中：N（z）为桩在z深度处承受的轴力。

dH／dz＝q（x，z）－p（x，z），桩侧土抗力q（x，z）可以由地基系数的Cz根据式（2）确定。

利用梁的弯矩与位移之间的微分关系（3），代入式（1）可推导出桩的挠曲微分方程如式（4），其中，EI为桩身抗弯刚度。

将桩离散成长度为l的桩单元，采用如图2的坐标系，得到轴向与横向荷载的平衡桩单元微分方程如式（5）。对轴向荷载作用下的横向受荷桩进行分析，可采用Galerkin法对式（5）进行求解。

图2 桩单元

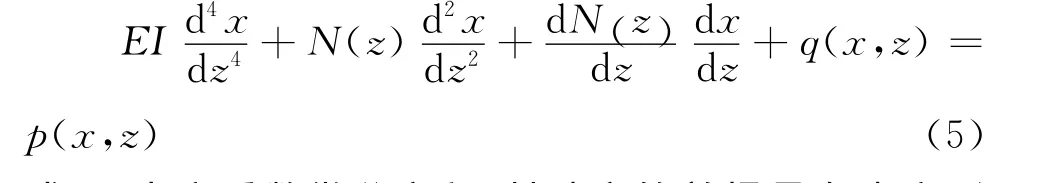
式（5）为变系数微分方程，其建立的前提是在小变形假设的基础上，因此对第3项的二阶微分是可以忽略的［3］。事实上，若离散后的梁单元足够小，可认为单个单元的N（z）相等，记为N。式（6）即为经典的基于梁柱原理的桩身单元微分表达形式：

横向荷载作用下梁单元刚度矩阵［K p］e的集成总体刚度矩阵［K p］，轴向荷载作用下梁单元的刚度矩阵［K N］e集成总体刚度矩阵［K N］，地基刚度单元矩阵［Ks］e集合成总刚度矩阵［Ks］。

式（6）离散后可写成如下的矩阵形式：

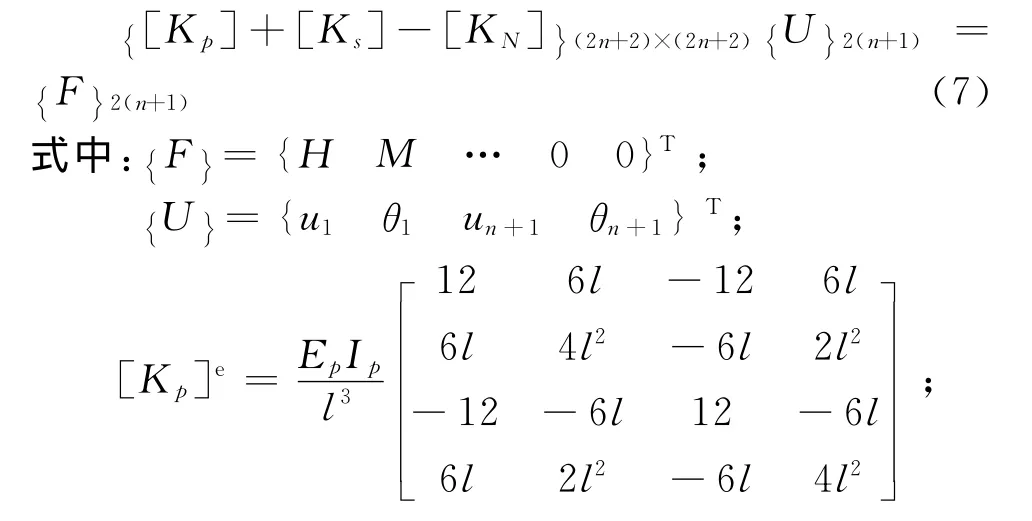
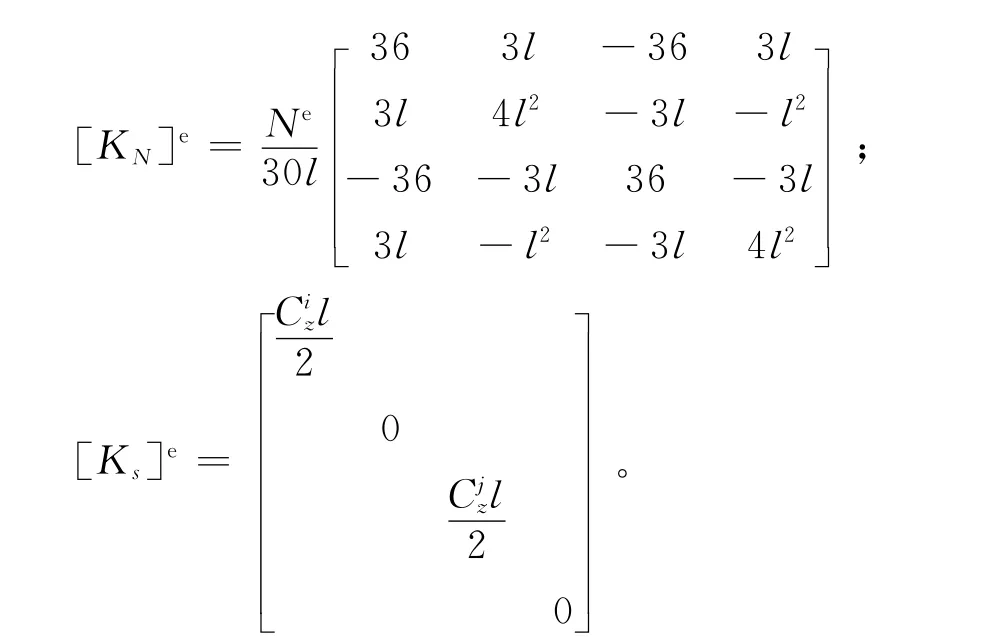
其中，n为分段数，Cz i表示深度z i处的地基系数，Ne为梁单元的轴向压力。除了特别说明，本文将N e统一视为桩顶荷载进行处理，在第3．4节说明此处理方法的合理性。

2 算例验证

为说明计算方法的实用性，将采用Cz地基系数为常数的假设进行计算，由地基系数分布形式带来的影响将在第3．3节中讨论。在计算中将地基作为连续弹性体确定地基系数的方法［3］，可采用 Vesic［11］提出的方法来确定Cz，该方法的特点是可将地基系数与土体的变形参数和土的泊松比联系起来，即：

式中，Es和υs分别为土的弹性模量和泊松比，其他参数定义同上。

算例1：本文方法与Poulos ＆Davis的弹性理论法［12］对比如图3所示，计算时桩长与直径比为L／d＝25，桩的柔度系数为K R＝Ep I p／（Es L4），土的泊松比为0．5，桩顶自由。桩顶作用有水平力或弯矩时的桩身弯矩分布曲线分别如图3（a）和图3（b）所示，对于桩身刚度较大的桩，本文解答与Poulos＆Davis分析结论是一致的，而对于桩身刚度较小的桩，本文方法的桩身弯矩要略大一些。

算例2：以文献［13］的有限元算例进行对比分析，桩长66 m，桩身弹性模量为28 000 MPa，桩径为1 m，土的弹性模量为50 MPa，泊松比为0．35，桩顶水平力400 k N，轴向荷载为3 000 k N。桩端持力层与桩周土相同。本文方法得到的单桩弯矩如图4所示，与有限元计算结果基本吻合，产生偏差主要是由于2种方法所采用的土体本构模型不同所致，文献［13］在有限元计算时土体采用的是弹塑性本构模型。

3 参数分析

本节将对轴向荷载作用下横向受荷桩进行参数分析，算例中的桩顶均为自由，桩身全部埋入土中。

图3 与Poulos ＆Davis计算结果弯矩对比图

图4 单桩弯矩对比图

3．1 轴向荷载的影响

Broms ＆Hansbo认为当轴向荷载小于屈曲临界荷载的10%时，轴向荷载对侧向挠曲一般只有很小的影响［14］。而对于软粘土，桩的临界荷载较低，有必要分析轴向荷载大于屈曲临界荷载10%的情况。为方便研究轴向荷载的影响，本文采用直桩挠曲荷载Ncr作为基准来分析轴向荷载的影响，Ncr可按式（9）确定［14］。

取桩长与直径比L／d＝25，土的泊松比υs＝0．25，桩土弹性比E p／Es＝1 000，桩顶作用的水平力和轴力分别为H＝πGsd2＝12．7%Ncr和N＝0、0．5H、H、2H、3H，桩身的弯矩和变形情况如图5所示，Gs为土体剪切模量。

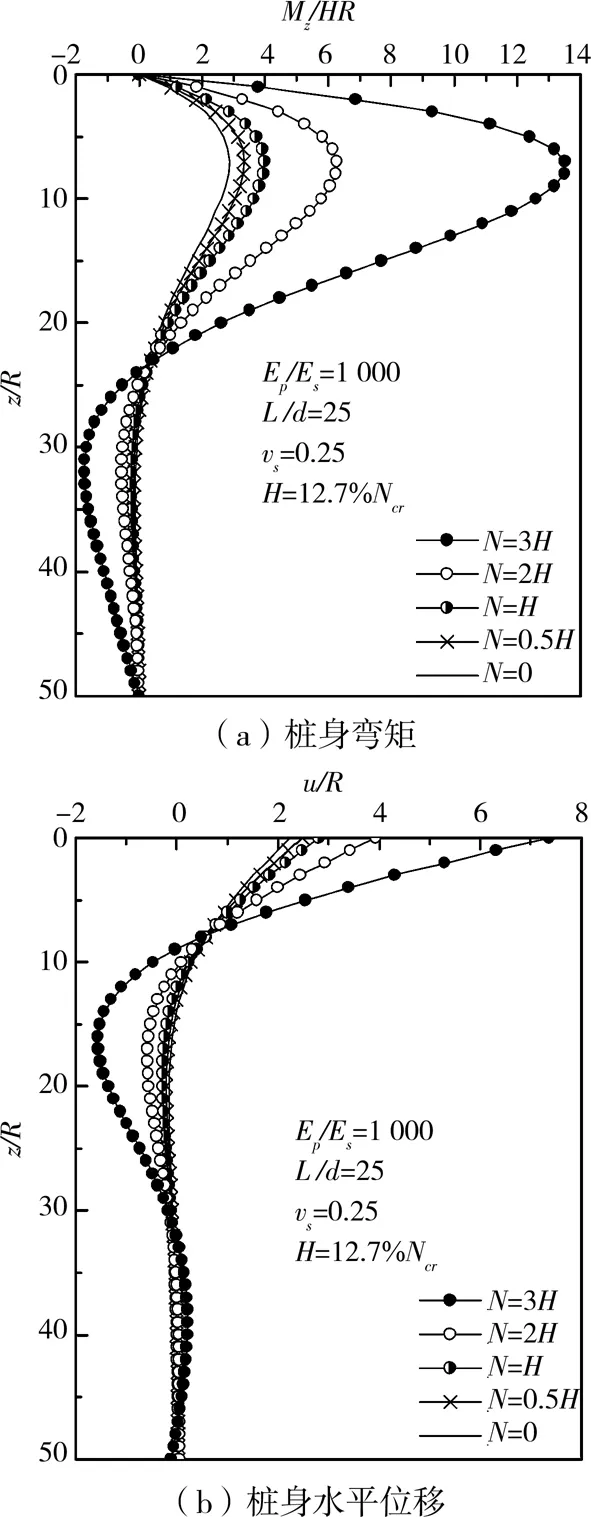
图5 不同轴向力作用下的水平桩

从图5中可看出，轴向荷载对桩身弯矩和侧向挠曲的影响主要在上部z／R＝0～20，水平桩最大弯矩发生在地面线以下z／R＝5～10范围，桩顶水平位移增加很快。当N＝0．5H，即6．35%Ncr时，最大弯矩增加16．6%，桩顶位移增加10．8%；当N＝H，即12．7%Ncr时，最大弯矩增加39．0%，桩顶位移增加25．1%。

随着N／H比值继续增加，桩身弯矩和挠曲增幅将快速增加，N／H越大，轴力对桩身弯矩越加显著。因此，在一定范围内，随着N／H比值的增加，桩身上部的内力和侧向挠曲增幅影响显著。轴向与横向荷载作用下的桩基内力和变形实际上是与两类荷载的大小密切相关，其主要原因是轴向荷载引起的桩基横向变形是非线性的。

3．2 桩土弹性模量比的影响

取桩长与直径比L／d＝25，土的泊松比υs＝0．25，桩土弹性比Ep／Es＝100、500、1 000、5 000、20 000，图6是在水平力H＝12．7%Ncr和轴力N＝H作用下，桩身的弯矩和变形受桩土弹性比的影响情况。

从图6中可看出，除Ep／Es＝100外，随着Ep／Es的增加，受轴向压力的影响，水平桩最大弯矩点逐渐下移，发生在地面线以下z／R＝5～15的距离内，桩顶位移减小。轴向荷载对桩身弯矩和侧向挠曲的影响主要在上部z／R＝0～25，当Ep／Es越大时，桩身上部弯矩增幅越大，而桩侧向挠曲变形趋于平缓。

图6 Ep／Es下水平力和轴力作用桩

3．3 地基系数的影响

地基系数为常量的假设对于非均质土可能会带来较大的偏差，本节主要分析地基系数的影响。取桩端土的弹性模量Esb＝1／4 000Ep，按式（8）计算桩底地基系数。计算结果如图7所示：1）表示地基系数为常数；2）表示地基系数为线性变化；3）取桩顶地表土的模量Es0／Esb＝1／3，得到的地基系数为梯形分布；4）取沿深度方向地基模量按Esb·（z／L）0．3分布，地基系数随深度呈抛物线变化。取水平荷载H＝12．7%Ncr进行计算，土的泊松比为0．35，L／d＝25。

图7 地基系数分布形式

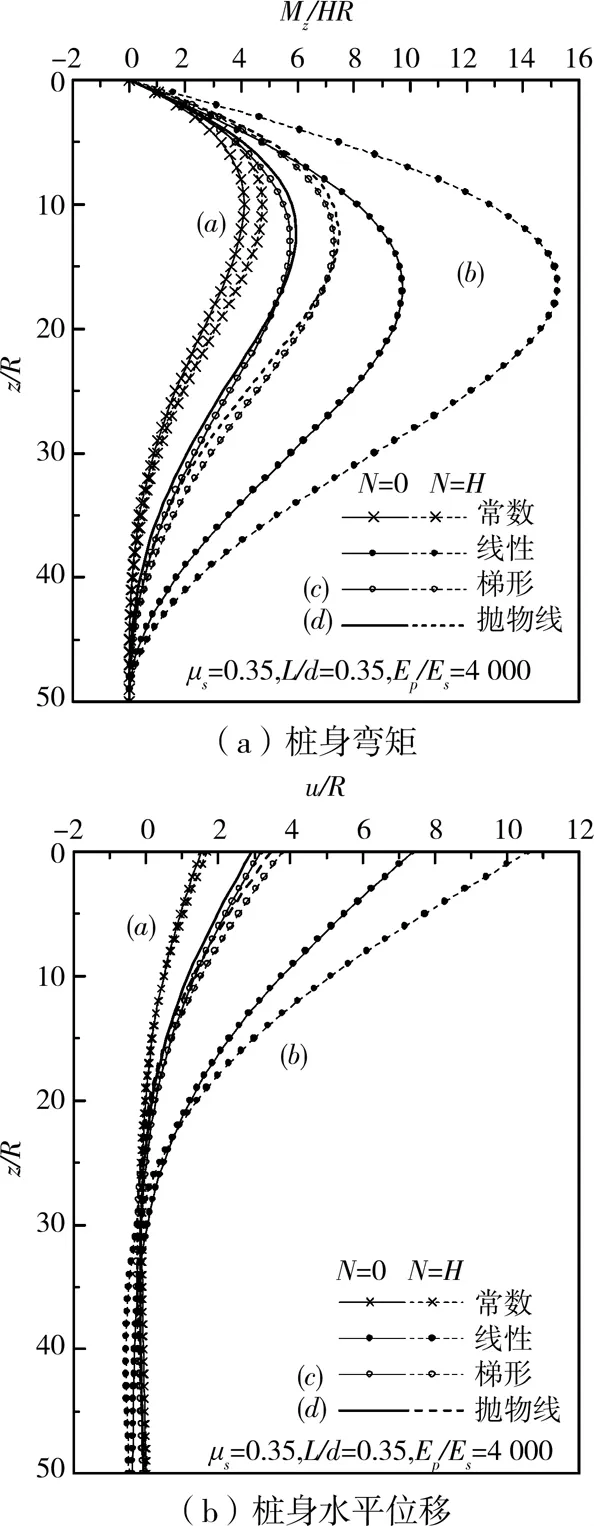
图8 地基系数下水平力和轴力作用桩

图8表明桩端地基系数相等时，上部地基系数的分布形状对于受轴向与横向荷载作用的桩基承载性状影响是不同的。其中，地基系数呈线性增加时，轴向荷载对水平载荷桩的影响是最大的，桩身最大弯矩值增加62．1%，桩身的最大弯矩位置明显下降，桩顶位移也显著增加；地基系数为常数时，影响是最小的，桩身最大弯矩值增加15．7%；地基系数呈梯形和抛物线形模式，计算得到桩身弯矩和位移大于地基系数为常数的情况，但小于地基系数呈线性增加的情况，桩身最大弯矩值分别增加27．5%和25．6%。

3．4 桩身轴力沿深度变化的影响

考虑桩自重及桩侧土的摩阻力的影响，轴力沿深度是减小的。但在工程设计中，通常假定横向受荷桩上作用的桩身轴力沿深度的分布是不变的。上文分析表明桩的最大弯矩通常是发生浅部，桩身轴力在此范围内衰减较小，而横向荷载对于桩的深部影响则较小。因此，当桩顶轴力较小时，将桩身轴力假定为常量是合理的。但是对于桩顶作用荷载较大时，桩身的轴力变化可能就不容忽视了。

为进一步分析此情况下的影响，图9给出了不同轴力水平下桩身轴力变化对桩身弯矩和变形的影响，其中轴身轴力变化是采用了Poulos弹性理论单桩计算方法，将桩身离散后得到各段单元的压力Ne，近似得到了沿桩身的轴力分布特性［12］。

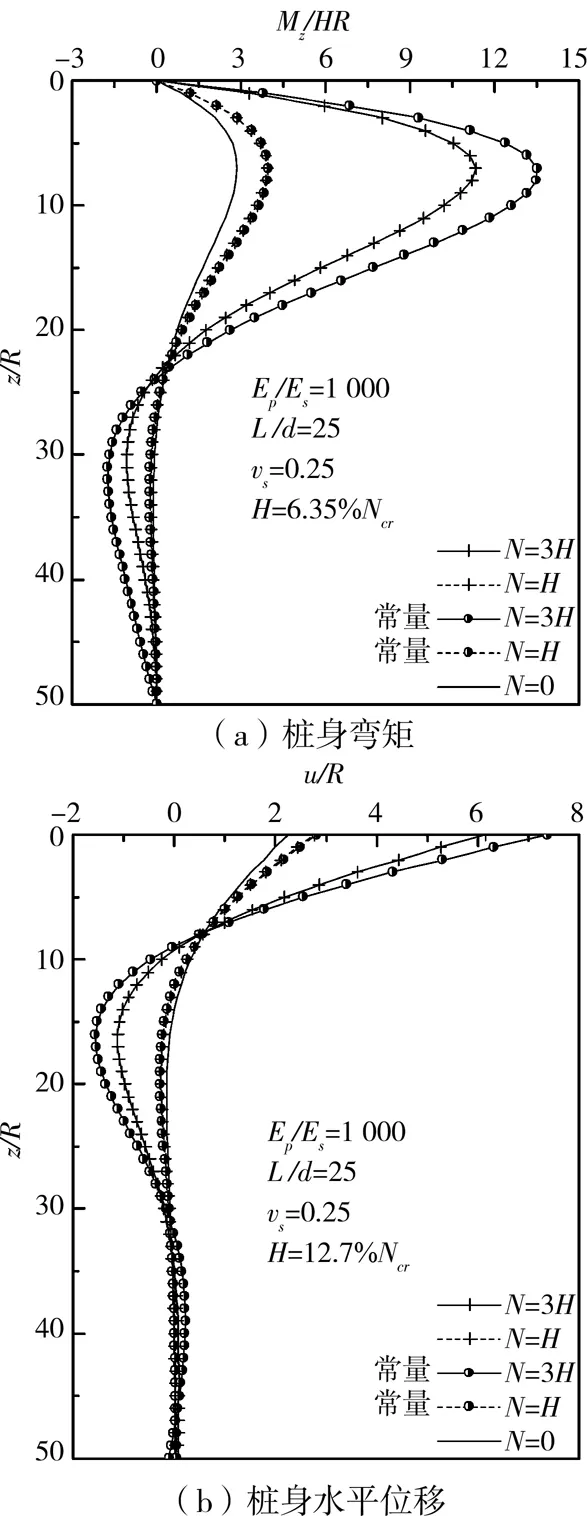
图9 轴力变化的对水平桩影响

图9的对比结果表明，轴力为常量的假定对桩身弯矩产生的影响在N／H较小时是可以忽略的，N／H较大时的影响则较为明显。但需要注意的是，此时桩基要承受轴向荷载可能已超过其极限承载力值。

4 结语

由于轴向荷载引起的桩基横向变形是非线性的，因而轴向荷载和水平向荷载共同作用下的桩基内力和变形实际上是与两类荷载的大小密切联系在一起的。一般地，基于桩的挠曲微分方程分析轴向荷载和横向荷载共同作用下的桩基问题，需要重视轴向荷载很大的情况。特别地，轴向荷载的存在对于柔性桩上部的内力和侧向挠曲影响比较显著，而对其深部的影响相对较小。

该文计算方法受到地基系数的分布形状的影响，地基系数呈线性增加时，轴向荷载对横向受荷桩的影响是最大的；而地基系数为常数时，其影响是最小的。除了在桩发生屈曲情况外，沿桩身方向轴向荷载的变化对水平桩的挠曲和弯矩的影响通常比较小。因而，轴向力作为常量的假设一般是可以满足工程实际要求的。

［1］肖世伟．轴向力对横向受力桩的影响［J］．西南交通大学学报，1990（4）：58－62．XIAO SHI－WEI．Effect of axial force on laterally－loaded piles［J］．Journal of Southwest Jiaotong University，1990（4）：58－62．

［2］赵明华．轴向和横向荷载同时作用下的桩基计算［J］．湖南大学学报，1987，14（2）：68－81．ZHAO MING－HUA．The calculation of piles under simultaneous axial and lateral loading［J］．Journal of Hu’nan University，1987，14（2）：68－81．

［3］横山幸满．桩结构物的计算方法和计算实例［M］．唐业清，吴庆荪．译．北京：中国铁道出版社，1984．

［4］POULOS H G．Analysis of pile groups subjected to vertical and horizontal loads［J］．Australian Geomechanics Journal，1974，4（1）：26－32．

［5］ZHANG L M，MCVAY M C，HAN S J，et al．Effects of dead loads on the lateral response of battered pile groups［J］．Canadian Geotechnical Journal，2002，39（3）：561－575．

［6］KARTHIGEYAN S， RAMAKRISHNA VVGST，RAJAGOPAL K．Numerical investigation of the effect of vertical load on the lateral response of piles［J］．Journal of Geotechnical and Geoenvironmental Engineering，2007，133（5）：512－521．

［7］ANAGNOSTOPOULOS C， GEORGIADIS M．Interaction of axial and lateral pile responses［J］．Journal of Geotechnical Engineering Division，ASCE，1993，119（4）：793－798．

［8］FEAGIN L．Lateral load tests on groups of battered and vertical piles［C］／／Philadelphia：the 56th Annual Conference American Society for Testing and Materials Special Technical Publication （ASTM STP），1953，154：12－20．

［9］KIM J B，BRUNGRABER R J．Full－scale lateral load tests of pile groups［J］．Journal of Geotechnical Engineering，ASCE，1976，102（1）：87－105．

［10］ROLLINS K M，PETERSON K T，WEAVER T J．Lateral load behaviour of full－scale pile groups in clay［J］．Journal of Geotechnical and Geoenvironmental Engineering，ASCE，1998，124（6）：468－478．

［11］VESIC A S．Bending of beams resting on isotropic elastic solids［J］．Journal of Soil Mechanics and Foundation Engineering，ASCE，1961，87（2）：35－53．

［12］POULOS H G，DAVIS E H．Pile Foundation Analysis and Design［M］．New York：John Wiley and Sons，1980．

［13］尹武先，姚文娟，程泽坤．轴－横向荷载作用下超长桩数值模拟［J］．水利水运工程学报，2009，7（2）：15－20．YIN WU－XIAN， YAO WEN－JUAN， CHENG ZEKUN．Numerical investigation on interaction of axial and lateral response for super－long pile［J］．Hydroscience and Engineering，2009，7（2）：15－20．

［14］BRAND E W，BRENNER RP．Soft Clay Engineering［M］．New York：Elsevier Scientific Pub．Co．1981．