新型钢框架梁柱节点滞回性能试验研究及有限元分析

何小辉，武振宇，张 扬，成 博

(1.哈尔滨工业大学 土木工程学院，哈尔滨150090；2.中国建筑设计研究院，北京100044)

钢框架梁柱节点作为结构的关键部位，起着传递结构构件(梁、柱)内力和协调结构变形的作用。在1994年美国Northridge地震和1995年日本Kobe地震中，以往被认为具有变形能力的梁柱焊接刚性节点发生了焊缝脆性破坏[1－2]，这引起了人们对焊接刚性节点延性性能的怀疑并激发了节点的改进研究，如美国的SAC项目。已有研究表明：通过改进焊接工艺、补强措施(加腋或盖板)和削弱措施(RBS)都可以实现焊接节点塑性铰外移至梁端截面，从而满足地震下的变形需求。然而梁截面塑性铰及其滞回耗能却不能减轻震后修复难度和费用。因此，采用角钢栓接的半刚性节点又被再次广泛关注，这类节点利用角钢既作抗力元件又作耗能元件，从而可以避免主体结构构件(梁、柱)发生塑性损伤，且其良好变形能力已为国内外试验证实[3－4]并建立了各种半刚性节点分析模型和试验节点数据库[5]。

基于现有角钢节点，利用螺杆对其进行改善，构造了一种新型钢框架梁柱耗能节点。通过节点的滞回性能试验和有限元分析，研究了不同延性的螺杆对节点性能的影响，对节点的受力机理、变形模式、弯矩－转角特性、力学性能(刚度、承载力、延性)和耗能能力进行了分析。最后，对该节点的优缺点进行评述，提出了进一步改进和深入研究的建议。

1 新型梁柱节点滞回性能试验

1.1 试件、加载装置及其加载方案

基于有效控制节点损伤部位(或塑性变形)仅限于连接件(角钢和螺杆)的设计思想和节点单调加载有限元分析，文中设计了3种共6个节点试验(图1)。如图1所示，梁和柱均为焊接H形钢，钢材为Q235B，截面为：HW200×200×10×12和 HW250×250×10×14，梁长lb＝0.6m，柱高lc＝0.97m。柱节点域设置了与梁翼缘等厚的横向加劲肋。焊接在梁翼缘上用于连接螺杆的连接板，其厚度与柱翼缘等厚，并设置加劲板(与梁腹板等厚)。与连接板相对应的梁截面设置了横向加劲肋，以有效约束梁翼缘的变形。为保证梁与柱具有充分可靠的接触，将梁端截面铣平。连接角钢为轧制角钢∟50×50×4，长度为70mm。采用10.9级M12的高强螺栓将角钢与柱、梁连在一起，并采用扭矩扳手对其施加规范[6]规定的60kN预拉力。这样制成的2个节点为ANGLE＿1和 ANGLE＿2。在此基础上，分别安置A3螺杆和A45螺杆就得到节点A3＿1、A3＿2和节点A45＿1、A45＿2。A3和A45螺杆分别由A3圆钢(热轧态)和45号圆钢(冷拔态)加工而成。螺杆工作段直径为6mm，长度为115mm(按0.03rad相对转角下具有设计可利用应变约6%考虑)，并采用8.8级M10的螺母进行连接。为了保证螺杆不出现拉、压空载及由此引起的受荷冲击、滑移现象，采用双侧螺母锚固方式；同时采用双螺母对顶拧紧的防松方法避免出现连接螺母松动、滑移现象。试验前假定螺杆处于零内力状态，本文通过粘贴在螺杆表面的应变片监测安装内力，并采用合理的施拧顺序达到既控制螺杆内力(应变片读数为±10με)又保证双螺母对顶拧紧且夹紧连接板或柱翼缘。

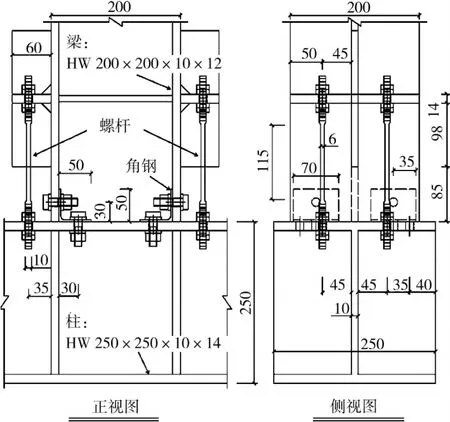
图1 试验节点详图

试验加载装置如图2所示，试件安置在L形反力架上。柱横卧，通过两端销轴与反力架上的支座连接。采用梁端加载方式，试验荷载P为拉压千斤顶施加的水平荷载，并通过力传感器输出。在梁端加载部位布置LVDT－1(差动变压器式位移传感器)以获取加载点的水平位移；在梁、柱交界处梁翼缘厚度的中点布置竖向LVDT－2～5(2、4位于右侧，3、5位于左侧)，测量梁端的张开间隙(亦可反映梁与柱的相对转角)；同时在距离柱翼缘外表面16mm处的梁翼缘中点布置水平LVDT－6，以监测梁端沿柱翼缘表面的滑移；另外，在柱两端铰接处布置YHD－7、8位移计以监测支座滑动。图2中还给出了螺杆编号示意图(螺杆编号与角钢编号相同)。图3给出了峰值点螺杆屈曲波峰矢高测量示意图，采用钢尺对所选螺杆(其屈曲位于梁柱节点平面内)单波屈曲的两个反弯点(位于螺杆工作段与螺纹段的过渡弧位置)和波峰点间的距离进行测量。

参照JGJ 101—96[7]和 CEES[8]，加载方案采用荷载－位移双控制方法；同时参考 AISC－341：SAC／BD－97／02[9]，以梁端侧移角θ0＝0.004 2rad作为“屈服后”循环位移增量步长。因此，试验加载方案具体为：1)根据有限元分析确定实验屈服荷载Fy，屈服前按力控制，分4级(每级为0.25Fy)，各循环1圈，且第4级荷载加载至名义屈服位移Δy＝0.004 2×lb＝2.5mm；2)屈服后按位移控制，位移增量为Δy，各循环3圈，直至8Δy或出现承载力下降；3)之后位移增量仍为Δy，各循环2圈，直至12Δy或发生角钢断裂。控制位移采用梁加载端LVDT－1所测位移。

图2 试验装置

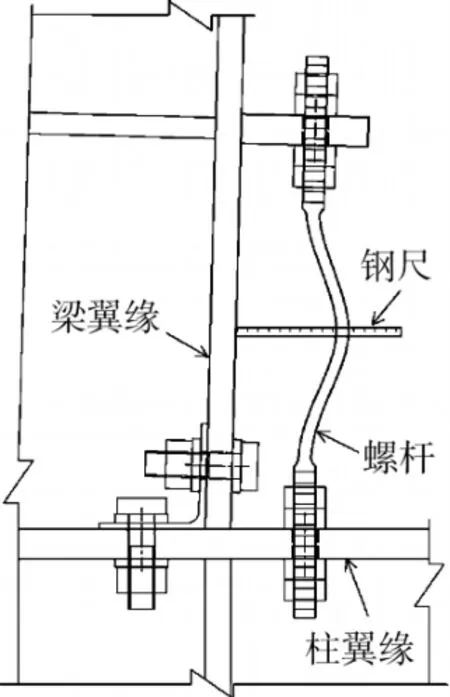
图3 峰值点屈曲波峰矢高测量示意

1.2 试件材性

为了更准确地预测和模拟节点性能，按照《金属材料室温拉伸实验方法》[10]对试验节点的各部件进行了材料拉伸实验，采用引伸计测量试件应变。由表1中数值可以发现：1)钢板均满足规范《碳素结构钢(GB／T 700—2006)》的性能要求；2)角钢因其生产工艺造成纵、横向的力学性能差异较大，主要体现在屈服强度和断后伸长率指标；3)A3钢杆具有可靠的延性，而A45钢杆断后伸长率较小，变形能力差，但极限强度很高。

表1 试验节点材性参数

1.3 试验现象及结果分析

1.3.1 试验现象 ANGLE节点的刚度和承载力只由内角钢提供，其延性取决于角钢的疲劳性能。循环加载过程中，受拉角钢塑性变形明显，受拉一侧梁翼缘脱离柱翼缘表面，且其间隙随梁端位移幅值的增大而增大；当梁端水平位移恢复至平衡位置(位移零点)时，梁端两侧翼缘均脱离柱翼缘表面(见图4(a))，该间隙亦随位移幅值的增大而增大；角钢裂缝主要出现在角钢根部倒角两侧边缘(见图4(b))；与柱翼缘相连的角钢肢，其螺栓孔附近的塑性变形较大，且在靠近角钢根部倒角一侧分布有沿螺栓孔径向的裂纹。由此可见，受拉角钢将形成3个塑性铰区域。根据观察，节点转动中心随作用荷载方向变化而在梁上、下翼缘，在峰值荷载时刻，可以认为节点转动中心位于梁上、下翼缘厚度的中点。

图4 试验节点变形示意图

A3和A45节点是在ANGLE节点基础上添加了钢螺杆，从而提高节点的刚度和承载力。循环加载过程中，梁翼缘两侧的螺杆将分别受压和受拉，受压一侧螺杆将发生单波弯曲屈曲(见图4(c)，对应某级循环荷载下的平衡位置时刻)，其最大屈曲波峰矢高大约可达20mm(A3)或12mm(A45)，但在节点弹性阶段(节点相对转角小于0.002rad)均未出现明显螺杆弯曲，其应变读数均未达到屈服应变且压杆应变读数稳定；在同一级位移荷载下，已经发生屈曲的螺杆不会在反向荷载作用下被完全拉直，也即反向荷载作用下受拉一侧螺杆不能充分发挥其潜在的抗拉能力，直接导致同级荷载下第2、3圈循环的连接承载力出现较大幅度下降；梁、柱间的相对变形仍旧以梁端与柱翼缘表面的间隙张开－闭合为特征；螺杆断裂并退出工作是逐步发生的(A3和A45螺杆分别始于8Δy和4Δy)，且断裂位置多在螺杆屈曲的上、下反弯点(也即圆角根部)(见图4(d))，少数在屈曲波峰位置。

ANGLE节点最终因角钢变形过大、裂缝贯穿而宣告节点破坏，A3和A45节点则因螺杆断裂而导致承载力大幅下降，剩余承载力仅为极限承载力的1／4～1／2，可以认为节点失效。

1.3.2 节点试验数据处理及结果分析 图5(a)—(d)给出了ANGLE、A3和A45节点的弯矩－相对转角滞回曲线及其骨架曲线。节点弯矩M由梁端反力P与梁长lb相乘而得，节点相对转角按θr＝((d3＋d5)／2－(d2＋d4)／2)／(db－tfb)计算，其中d2～d5为LVDT－2～LVDT－5测得的位移，db为梁截面高度，tfb为梁翼缘厚度。表2给出了试验节点的部分结果，表中数值为正负向平均值。

图5 试验节点弯矩－相对转角滞回曲线及骨架曲线

表2 试验节点结果汇总

由图5及表2中数据可以发现：1)3种节点的初始弹性刚度平均值为：ANGLE(9.7)＜ A3(19.3)≈A45(18.5)，可见添加螺杆提高了节点刚度近1倍，而A3和A45节点具有相近的刚度值，因所用螺杆均为相同截面积的钢螺杆；2)3种节点的承载力差别非常明显，添加螺杆可以提高节点承载力，且螺杆强度越高，承载力提高幅度越大；3)ANGLE节点可以满足EC8[12]规定的DCH(高延性级)节点转动变形θp＝0.035rad的要求，A3节点则满足DCM(中等延性级)0.025rad的要求，而A45节点则属于EC8中的DCL(低延性级)类。由此可见，3种节点的转动能力相差非常大，螺杆连接因螺杆疲劳断裂而偏小(特别是A45节点)。影响螺杆疲劳断裂的因素主要有：1)与螺杆的设计可利用应变较大有关(θr＝0.03rad对应的螺杆应变约为0.03×229／115＝0.059 7≈6%)，导致螺杆的抗疲劳断裂性能较差；2)与螺杆自身的延性性能有关，冷拔45号圆钢具有高强低延性特点，而A3圆钢具有较好的延性性能；3)与螺杆加工质量有关，文中螺杆采用车削方式加工，而在螺杆两头的圆弧倒角部位存在明显的打刀刮痕，且其直径相对于螺杆中部偏小，这就造成螺杆断裂不同步，且断裂部位以螺杆两头为主(每个节点仅1根螺杆在中部发生断裂)；4)与螺杆自身初始弯曲及装配后螺杆倾斜度有关，该因素的影响相对较小，因所用螺杆具有较好的平直度，且即便是理想无缺陷螺杆也必定处于偏心受压，且偏心程度随θr的增大而增大；5)与螺杆弯曲屈曲有关，屈曲螺杆将在3处(2个反弯点和波峰点)产生塑性应力和应变集中，从而加大该部位的应力或应变变化幅值，使螺杆的疲劳性能恶化，因此若能采取措施抑制螺杆屈曲，将有利于改善螺杆疲劳性能，进而改善节点性能。

由试验滞回曲线不难看出，3种节点具有相似的力学行为。图6所示为ANGLE＿2滞回曲线的1.5圈，根据该图对节点塑性加载下的受力过程进行描述：1)AB为卸载段，首先主要发生原受拉角钢弹性恢复，随着原受压一侧梁翼缘与柱翼缘间的挤压应力减小，原受压一侧角钢将发生弹性恢复并使梁外推，促使梁翼缘与柱翼缘脱离，节点转动中心也将逐渐向另一侧转移，因此AB段存在一个刚度转折点(对应梁翼缘与柱翼缘脱离或失压)；2)BC为“间隙”加载段，“间隙”是指梁端两侧翼缘均与柱翼缘脱离，该阶段以低刚度(约149kN·m／rad)为特征，捏缩滞回曲线，将使角钢的拉、压角色互换，节点转动中心最终移向另一侧。其刚度低是由于两侧角钢同步串联作用(刚度减半)、角钢塑性和转动中心偏移等因素综合引起的；3)CD为“闭合”加载段，“闭合”是指梁原受拉一侧翼缘与柱翼缘表面接触并产生挤压应力，该阶段刚度(约376kN·m／rad)明显增大，主要是由于两侧角钢转为同步并联作用(以受拉角钢为主)，且转动中心固定在梁、柱翼缘接触位置。在接近峰值荷载附近出现明显的刚度转折，这是角钢塑性及裂缝向周边进一步扩展引起的。后续加载则是对上述3个过程的重现与往复，并伴随有同级荷载的强度退化和跨级荷载的强化现象。这里还需要指出：1)BC段随加载幅值增加而延长；2)随着角钢塑性损伤的累积和裂缝的不断扩展，2个加载过程的刚度都将逐渐减小，且减小速率呈增长趋势，CD段甚至趋于消失。A3、A45节点具有相似的受力特点(螺杆与角钢是并联作用的)，只需对受拉螺杆强化和受压螺杆屈曲加以考虑即可。但受压螺杆屈曲将导致更大程度的曲线捏缩现象。

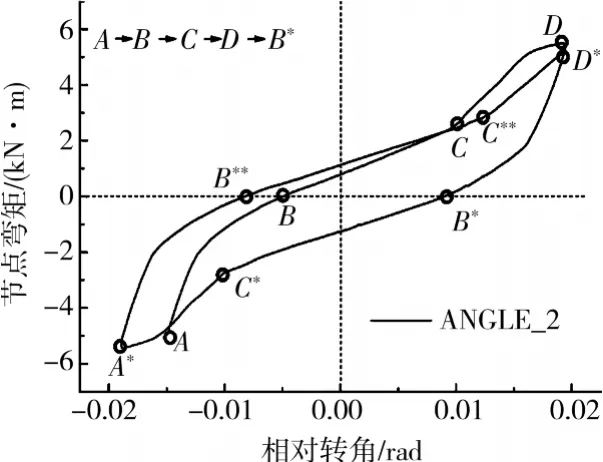
图6 节点受力作用机理示意

下面结合图5—6分析一下节点的强度、刚度退化现象：1)所有节点因角钢塑性损伤和螺杆屈曲而出现同一级荷载下的循环强度退化，并趋于稳定(即退化幅度急剧减小)；2)所有节点塑性加载阶段的滞回曲线(与骨架曲线的平台段对应)均有明显捏缩，具有二阶段加载特性，且捏缩平台段随角钢塑性变形和螺杆屈曲变形的增大而延长；3)ANGLE节点的角钢在5Δy(θr≈0.018rad)就出现了裂纹，但节点仍具有一定的强化能力，直至超过θr≈0.03rad才出现强度退化(角钢裂缝已扩展较长)；4)塑性加载范围内A3和A45节点的承载力强化较小，尤其是正向骨架曲线近乎水平线，这主要是由于受拉区螺杆和角钢的材料强化被受压区螺杆的弯曲屈曲弱化抵消了；5)A45节点在螺杆尚未断裂前就出现了承载力退化，且有明显的循环内退化，这主要是由于高强钢材变形能力较差(有限变形下就会进入类似于材料单调拉伸曲线的下降段)和螺杆的低周疲劳损伤。

图7为部分试验节点的累积能量耗散值EdT(滞回曲线包围面积的累加，kN·mrad)随加载循环圈数n的变化曲线，其中A3、A45节点不考虑螺杆断裂后的能量耗散值。由图中曲线可以发现，随n增大，EdT逐渐加速增大；由于螺杆塑性变形对节点耗能的贡献，A3、A45节点在相同循环圈数下的EdT明显大于ANGLE节点；曲线A45与A3在n＝9相交。这主要是由于高强钢杆对节点相对转角的限制作用(螺杆强度越高，相同θr所需的外部荷载就越大，从而梁、柱构件的弹性变形更大，所需的梁端侧移也越大)和塑性区的节点承载力强化较小(故梁、柱构件弹性变形对梁端侧移的贡献相对稳定，从而θr占梁端侧移角的比例将随n增大而逐步增大)，从而造成小位移下(n＜9)即使A45节点承载力远大于A3节点，A45节点的EdT仍小于A3节点，和大位移下(n＞9)A45节点的EdT反超A3节点的现象。图8为部分试验节点的单圈能量耗散系数E[7]。由图8曲线可以看出，塑性区同级荷载下螺杆连接具有更高的E值；同级荷载下第1圈的E值明显高于第2、3圈，另外还需剔除弹性阶段的数据点，故采用n＞5且各级荷载下第2、3圈的E值来观察其变化趋势：EANGLE随循环位移幅值增加呈线性增长，变化范围为0.35～1.31；EA3则基本维持稳定，变化范围为0.96～1.20；EA45也随循环位移幅值增加而增长，变化范围为0.55～0.87。综上所述，A3节点具有更好的耗能能力。

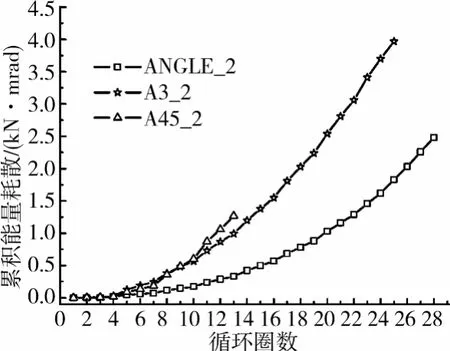
图7 节点累积能量耗散曲线

图8 试验节点单圈能量耗散系数

2 试验节点有限元分析

2.1 节点有限元模型介绍

采用大型通用非线性有限元软件ANSYS 8.1对试验节点进行模拟分析，综合考虑了材料、几何和接触非线性[13]。按照试验节点实际尺寸建立有限元模型，如图9所示。其中梁、柱、角钢、螺栓和螺杆均采用三维实体单元SOLID45；采用摩擦接触单元CONTA173和TARGE170考虑了各部件间(角钢、梁、柱、螺栓和螺杆)的相互作用，摩擦系数取0.3；高强螺栓预拉力通过预张拉单元PRETS179施加。有限元模型的边界条件与试验节点一样，对柱两端及梁端施加铰接约束(其中梁端只约束垂直于梁轴线的水平位移)。本文在单元划分时，对关键部位(如应力梯度大的部位、角钢、螺栓孔周边及螺杆等)采用较小的网格尺寸。考虑到模型和边界条件的对称性，沿梁、柱腹板中面取1／2模型进行分析，以节约计算时间。另外，模型考虑了角钢肢垂直度偏差δa对试验节点的装配影响，δa取0.2mm和2mm(后者为实测平均值)2种情况，相应有限元算例分别记为：xxx＿femb和xxx＿fem，其中xxx代表ANGLE、A3和A45。参照试验加载方案，有限元计算分2步：1)施加高强螺栓预拉力，且先施加柱翼缘螺栓再施加梁翼缘螺栓；2)施加梁端循环位移荷载，位移序列与试验一致(并用位移取代屈服前的力控制)。

计算模型采用多线性随动强化的钢材本构模型，Von Mises屈服准则及相关流动法则，并根据实测材性确定相关参数，其中角钢模拟时采用横向性能。鉴于角钢和螺杆的应变较大，采用真应力－应变关系替换工程应力－应变关系。另外，10.9级高强螺栓和8.8级高强螺母则参照规范GB 3098.1确定其屈服强度分别为940MPa和640MPa，极限强度分别为1 040MPa和800MPa。所有板材和角钢的泊松比取为0.28，钢杆和高强螺栓的泊松比取为0.3。如图10所示，图(a)对应有明显屈服平台的材料(钢板、A3钢杆)，图(b)对应无明显屈服强度的材料(角钢、A45钢杆和高强螺栓及螺母)。

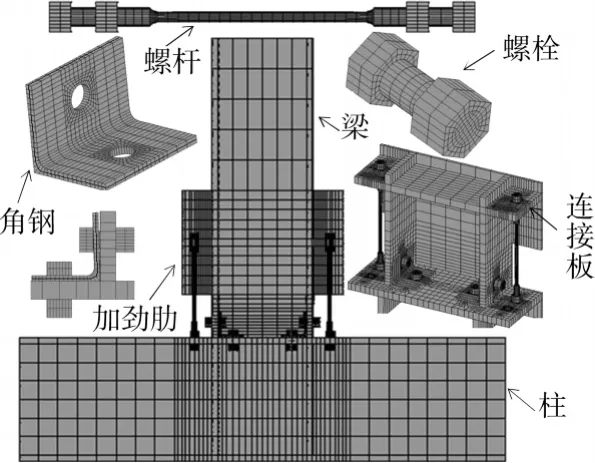
图9 试验节点有限元模型

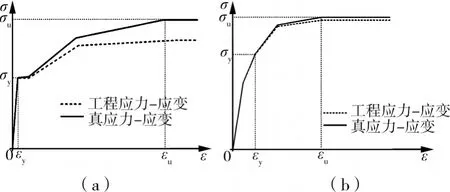
图10 材性模型示意图

2.2 节点有限元计算结果分析

由于文中节点有限元模型不能考虑塑性累积损伤和裂缝开展，承载力将因材料强化而不断增长，因此最大计算位移分别取为：试验ANGLE节点出现强度退化和A3、A45节点出现螺杆断裂对应的梁端侧移。

图11给出了有限元计算所得的节点弯矩－相对转角滞回曲线及骨架曲线，并给出了相应节点的试验曲线以作对比。表3给出了部分节点性能参数，其中屈服弯矩和屈服相对转角的取值方法与表2一样，极限弯矩是指有限元计算所得的最大承载力。由图11和表3可以得到以下几点结论：1)当对具有角钢肢垂直度偏差的连接角钢施加高强螺栓预拉力时，梁翼缘角钢肢发生变形并夹紧梁翼缘，从而提高节点刚度。一旦角钢因受拉而发展一定的塑性变形，这种预应力刚化效应就会消失。因此，角钢垂直度偏差对节点在小变形下的性能影响较大，δa＝2mm的节点初始弹性刚度约为δa＝0.2mm的4倍(ANGLE)或2.5倍(A3、A45)，且具有非线性伪弹性特性，但承载力仅略微偏大，屈服相对转角则小2～3m／rad不等；2)考虑δa影响的计算滞回曲线和骨架曲线与试验曲线吻合较好，屈服相对转角、屈服弯矩和极限弯矩的平均值均略有偏大，且ANGLE＿fem节点的曲线捏缩程度较试验偏小；3)文中计算滞回曲线均能体现出强度的同级弱化和跨级强化以及刚度退化特性，但是试验节点的同级强度退化随位移幅值增大而加大，而计算节点则反之；4)有限元计算所得初始弹性刚度均明显小于试验节点测试结果，其原因有2方面：1)计算模型的完备性及准确性，首先本文节点模型没有考虑梁自重、梁端加载装置的重量及竖向弹性约束对梁柱界面间隙张开的抑制作用，其次有限元接触分析无法避免一定的接触容许穿透值；2)试验测试的准确性，首先试验加载控制位移(也即计算控制位移)不是梁柱界面间隙位移，其次加载控制位移存在少量滑移现象，导致计算位移取值偏大，再则试验过程中位移计固定不动，没能考虑转动变形的影响。鉴于节点非线性较强和初始弹性刚度难于准确测试，AISC－360[14]提出采用割线刚度Ks＝Ms／θs来描述正常使用荷载下的连接反应。

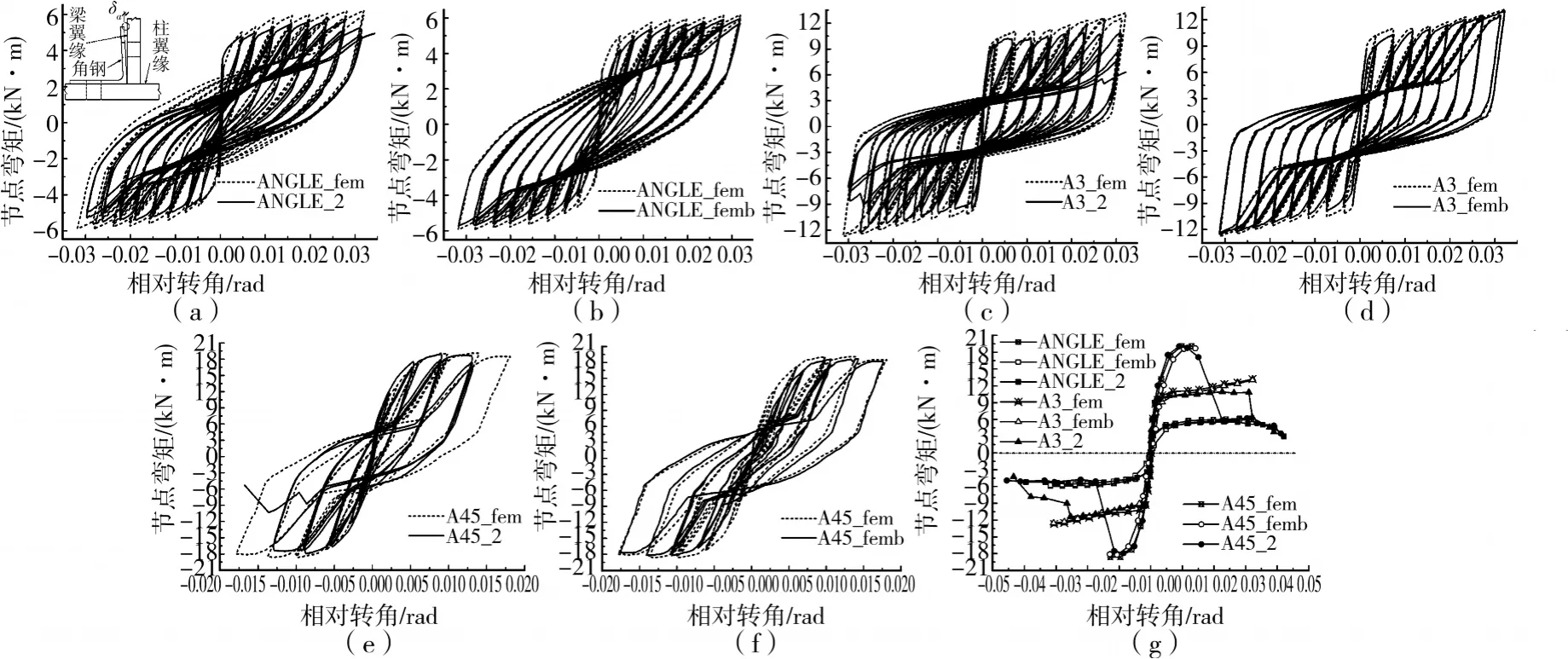
图11 节点弯矩－相对转角滞回曲线及骨架曲线

表3 有限元计算结果汇总

图12为xxx＿fem计算节点的变形图和角钢、螺杆应力云图，其中图12(a)与图4试验节点的变形模式相同，即梁端位移零点时刻，梁端两侧翼缘均脱离柱翼缘表面，角钢塑性变形明显，两侧螺杆均呈弯曲状态。图12(b)为ANGLE节点角钢应力云图，其塑性应力分布区域与试验角钢的裂缝观察是一致的，对受拉角钢形成3个塑性铰给予了验证。图12(c)为A3节点在7Δy第3圈峰值时刻的螺杆Mises应力云图，压杆屈曲明显，在两个反弯点和波峰点的外侧(即受拉一侧)具有最大应力，约达540MPa(远高于材料屈服强度，略小于抗拉强度)；而拉杆最大应力约为480MPa，在杆弯曲屈曲的内侧(即受压一侧)具有较大的应力，且应力沿杆长和截面分布不均匀，这与试验中观察到的同级荷载第2、3圈循环的受拉螺杆不能被完全拉直的现象一致(但试验更为明显)。另外，试验节点的螺杆单波屈曲方向具有很强的随机性，取决于螺杆自身缺陷和安装误差等因素；而计算节点的螺杆屈曲方向则取决于计算误差(源于材料、几何、接触非线性及网格规划)引入的数值缺陷，从而导致两侧无初始缺陷的螺杆产生不同方向的屈曲模式。

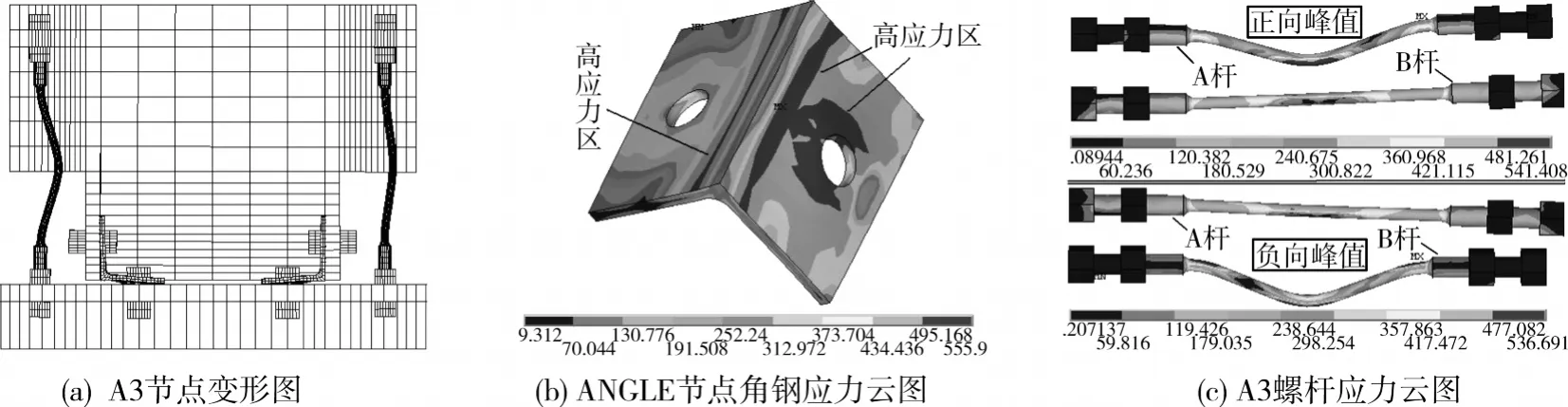
图12 计算节点变形图及应力云图

综上所述，采用本文节点有限元模型xxx＿fem可以较好地模拟试验节点的滞回性能，反映节点的变形模式。同时也表明：对于薄柔角钢应该考虑角钢垂直度偏差引起的节点刚化效应，才能更准确的模拟节点在小变形下的力学行为。

3 结论

通过6个节点的模型试验和有限元分析，对所提出的新型钢框架梁柱耗能节点的力学性能和耗能能力进行了研究。主要结论如下：

1)ANGLE节点与传统的顶底角钢节点一样，具有很好的延性性能；角钢的变形模式、裂缝分布及有限元应力云图证明受拉角钢将形成3个塑性铰。

2)角钢垂直度偏差将使角钢连接产生预应力刚化效应，提高节点初始弹性刚度，且使节点在小变形下具有非线性伪弹性特性。

3)螺杆连接可以提高节点刚度和承载力，其提高幅度取决于所用螺杆截面积大小、材料强度和螺杆的节点弯矩力臂大小；然而，所用螺杆的抗疲劳断裂能力严重影响着节点延性，影响其疲劳性能的因素有：螺杆设计可利用应变大小、螺杆材料延性、螺杆屈曲、螺杆加工质量及安装误差等。

4)ANGLE、A3和A45节点的滞回曲线具有相似性，具有明显的捏缩现象，这主要是由于梁柱界面的间隙张开－闭合特性、角钢塑性和螺杆屈曲引起的。

5)采用良好延性螺杆的A3节点具有更好的耗能能力，即具有更大的能量耗散值和具有较大且稳定的单圈能量耗散系数。

6)试验节点因角钢塑性损伤、裂缝扩展和螺杆屈曲及疲劳损伤而出现性能退化。

7)节点有限元模型可以较好地模拟节点在出现明显强度退化或螺杆断裂前的滞回性能和变形模式，为进一步的变参数有限元分析提供了试验和理论基础。

由此可见，文中提出的螺杆连接节点具有如下优点：1)较之角钢节点，提高了节点刚度、承载力和耗能能力，增加了节点冗余度，实现多重耗能，结构安全可靠度增大；2)节点受力清晰，传力路径明确，且螺杆材料利用充分；3)通过角钢和螺杆的尺寸参数调节可以满足节点的不同设计需求；4)无现场焊接，制作安装方便，易于保证施工质量；5)震后节点受损部件易于修复(只需替换角钢、螺杆)。然而，本文分析亦透露出现有节点的不足：1)滞回曲线捏缩大(捏缩程度大于角钢节点)；2)螺杆疲劳断裂过早，降低了节点转动能力；3)螺杆连接因螺杆断裂而失效，呈脆性破坏特征。对于第2、3点，可以通过采用延性性能更好的螺杆和减小螺杆的设计可利用应变值(如文献[15]建议取防屈曲支撑工作段设计应变εb≤3%)，提高螺杆的疲劳性能，避免设计地震或强震下出现螺杆断裂；至于滞回曲线的捏缩问题则可以从多个方面着手，如采用抑制螺杆屈曲的约束套管[16]或消除滞回滑移的摩擦楔形块－弹簧装置[17]、设置PT杆[18]使梁端翼缘与柱翼缘提早接触，但各种措施对节点性能的改善效果和对螺杆疲劳性能的影响有待进一步研究和试验验证。

另外，本文试验节点为模型节点，节点刚度和承载力均较小，因此有必要开展大尺寸或足尺节点试验研究和有限元分析，对与角钢、螺杆相连的部件和节点细部构造予以充分考虑和合理设计，确保设计节点能够达到实际工程节点的性能要求。

[1]NAKASHIMA M，INOUE K，TADA M.Classification of damage to steel buildings observed in the 1995Hyogoken－Nanbu earthquake[J].Engineering Structures，1998，20(4－6)：271－281.

[2]CHARLES W.ROEDER.Connection performance for Seismic design of steel moment frames[J].J.Struct Eng，2002，128(4)：517－525.

[3]ATOROD AZIZINAMINI，JAMES B，RADZIMINSKI.Static and cyclic performance of semirigid steel beam－tocolumn connections[J].J.Struct Eng，1989，115(12)：2979－2999.

[4]王新武，李和平，蒋沧如.梁柱角钢连接节点的滞回性能实验研究[J].华中科技大学学报：自然科学版，2003，31(8)：13－15.WANG XIN－WU，LI HE－PING，JIANG CANG－RU.Hysteretic behavior of angles beam－column connections[J].J.Huazhong Univ.of Sci.＆ Tech：Nature Science Edition，2003，31(8)：13－15.

[5]陈惠发.钢框架稳定设计[M].周绥平.译.上海：世界图书出版公司，1999.

[6]JGJ 82－91钢结构高强螺栓连接的设计、施工及验收规程[S].

[7]JGJ 101－96建筑抗震实验方法规程[S].

[8]ECCS：Recommended Testing Procedure for Assessing the Behaviour of Structural Steel Elements under Cyclic Loads[S].First Edition 1986.

[9]ANSI／AISC 341－05Seismic Provisions for Structural Steel Buildings[S].Chicago，2005.

[10]GB／T 228—2002金属材料室温拉伸试验方法[S].

[11]GB 50152—92混凝土结构试验方法标准[S].

[12]PrEN 1998－1：Design of Structures for Earthquake Resistance：General Rules，Seismic Actions and Rules for Buildings[S].2003.

[13]ANSYS Inc.Theory Reference[M].ANSYS Documentation，Release 8.1.

[14]ANSI／AISC 360－05：Specification for Structural Steel Buildings[S].Chicago，2005.

[15]程光煜，叶列平，崔鸿超.防屈曲耗能钢支撑设计方法的研究[J].建筑结构学报，2008，29(1)：40－48.CHENG GUANG－YU，YE LIE－PING，CUI HONGCHAO.Study on the design method of bucklingrestrained brace[J].Journal of Building Structures，2008，29(1)：40－48.

[16]MARRIOTT D J，PAMPANIN S，PALERMO A，et al.Shake－table testing of hybrid post－tensioned precast wall systems with alternative dissipating solutions[C]／／The 14th World Conference on Earthquake Engineering，October 12－17，2008，Beijing，China.

[17]TAKAO TAKAMATSU，HIROYUKI TAMAI.Nonslip－type restoring force characteristics of an exposedtype column base[J].J.Constr Steel res，2005，61：942－961.

[18]CONSTANTIN CHRISTOPOULOS，ANDRE FILIATRAULT，CHIA－MING UANG，et al.Posttensioned energy dissipating connections for moment－resisting steel frames[J].J.Struct eng，2002，128(9)：1111－1120.