钢筋混凝土柱非线性特性的分析方法

张 勤，贡金鑫，姜凤娇，2，朱绩超，3

(1.大连理工大学 建设工程学部，辽宁 大连116024；2.大连海洋大学，辽宁 大连116023；3.大连交通大学，辽宁 大连116028)

在轴向和水平荷载作用下，钢筋混凝土柱的总侧向变形由弯曲变形、剪切变形和柱底部的纵筋滑移变形组成[1－2]。对于弯曲变形，可通过截面分析得到的弯矩－曲率关系及塑性铰模型计算；而对于其他两种变形，尤其是剪切变形的计算则相对复杂得多，国内外对此进行的研究也不多。文献[3－5]分别采用不同的分析方法来建立包含剪切影响的柱荷载－变形关系，但这些方法的分析过程均非常复杂且存在着大量的迭代计算，在实际工程应用中存在着一定的局限性。为此，根据钢筋混凝土柱的受力特点，提出一种简化的荷载－变形曲线和卸载刚度计算方法，即首先按传统的弯曲截面分析和塑性铰模型确定柱的荷载－弯曲变形曲线，再通过对柱试验结果的统计分析，给出考虑柱剪切和纵筋滑移变形综合影响的修正系数，进而得到柱荷载－变形的全曲线；同时通过对试验结果的分析，给出卸载刚度与柱初始刚度的关系。最后采用该文提出的模型，以一单自由度体系为例进行poshover分析，研究了剪跨比、轴压比等参数(反映剪力的影响)对柱地震变形反应的影响。

1 弯曲荷载－变形曲线计算

主要研究弯曲破坏和弯剪破坏柱。在实际工程中，柱的剪力和弯矩总是同时存在的，所以弯曲破坏也只是以弯曲作用为主，剪力起的作用小，可以忽略，但难以取得忽略剪力的界限。在分析中，所有柱均以弯剪破坏看待，弯曲起主要作用时考虑剪切修正的系数小，剪切作用明显时修正的系数大。

1.1 材料本构关系

1)钢筋应力－应变关系采用 Esmaeily ＆ Xiao[6]的三线段强化模型，并认为钢筋受压时的本构关系与受拉时相同。

2)保护层混凝土采用 Marder等[7]的应力－应变模型；核心混凝土采用Saatcioglu－Razvi约束混凝土模型[8－9]。

1.2 弯曲荷载－变形曲线计算

柱顶弯曲变形Δf与塑性铰区域曲率φ的关系为[10]：

式中，φ为柱塑性铰区的转动曲率；φy为构件的屈服曲率，对应于截面最外侧纵向受拉钢筋首次屈服时的曲率；lp为塑性铰长度，按 Priestley ＆ Park[11]的模型计算：

式中，fy为纵筋屈服强度；d为纵筋直径，H为柱高。

考虑P－Δ效应的影响，柱的水平荷载按下式计算：

式中，P为柱所受的初始轴向压力；Δf为柱顶的弯曲变形。

2 弯剪荷载－变形曲线计算

2.1 基本方法

钢筋混凝土柱的总侧向变形由弯曲变形、剪切变形和滑移变形组成。对于弯剪破坏的柱，总侧向变形中的剪切变形分量所占的比例较大，特别是在混凝土开裂和纵筋屈服后，总的特征是，混凝土开裂后剪切变形加大，接近或超过按弯曲变形计算的值，纵筋屈服后承载力降低，明显小于按弯曲计算的值，如图1所示。本文分析采用的方法是，纵筋屈服前修正按弯曲理论计算的变形，纵筋屈服后修正按弯曲理论计算的承载力，即

纵筋屈服前的水平位移和荷载为：

纵筋屈服后的水平位移和荷载为：ΔT＝kΔ(χ)·

式中，kΔ(χ)为纵筋屈服前剪切、滑移变形的修正系数；Ff为变形为ΔT时按弯曲理论计算的柱的水平荷载；(kFμΔ)为纵筋屈服后考虑剪切及滑移影响的荷载修正系数。

图1 计算曲线与试验曲线比较

2.2 纵筋屈服前变形的修正

纵筋屈服前可认为柱处于弹性反应阶段，该阶段的总侧向变形ΔT和弯曲变形Δf之间的关系可采用系数kΔ(χ)来修正。系数kΔ(χ)考虑了剪切及滑移变形的影响并与反映柱基本特征的参数χ有关，可通过柱实际屈服位移Δty和计算的屈服位移Δfy之间的关系来建立，即：

式中，Δfy为按弯曲理论计算的柱屈服位移，对应于截面最外侧纵向受拉钢筋首次屈服时的位移，按式(1)计算；Δry为柱实际屈服位移，对应于弯矩为My时试验骨架曲线上的实测位移(My为按弯曲理论计算的屈服弯矩，对应于截面最外侧纵向受拉钢筋首次屈服时的弯矩，由截面分析得到)，Δry的计算过程如图1所示；kΔ(χ)，是关于参数χ的函数。

从PEER结构抗震性能试验数据库[12]中选取了34根钢筋混凝土柱试件进行分析，可得：

式中，λ为柱剪跨比；n为柱轴压比；ρs、fy分别为纵筋配筋率和屈服强度。屈服位移比值(Δry／Δfy)与参数χ的关系如图2所示。ΔTy／Δry的平均值为1.007；标准差为0.187。

图2 屈服位移比(Δry／Δfy)与参数χ的关系

2.3 纵筋屈服后承载力的修正

纵筋屈服后柱进入弹塑性反应阶段，通过建立柱水平荷载Ff的修正系数kFμ()Δ来考虑剪切及滑移的影响，即以式(4)修正后的荷载－变形曲线为基础，在相同的变形下，柱的水平荷载按下式计算：

式中：FTf为变形为ΔTf＝ΔT时考虑剪切及滑移影响计算的柱的水平荷载；kFμ()Δ根据试验结果确定为相同变形下柱的实际水平荷载与按弯曲理论计算的水平荷载之比，与柱的相对位移系数μΔ(μΔ定义为柱屈服后的位移ΔT与实际屈服位移Δry的比值)有关。

通过对纵筋屈服后柱试验骨架曲线与所计算的荷载－变形曲线的比较，得到各试验柱荷载修正系数kF(μΔ) 与相对位移系数μΔ的关系(图3)：

式中，ψ为试验确定的系数，与影响柱剪切及滑移变形的因素有关，经对34个柱试件的分析，可按下式计算：

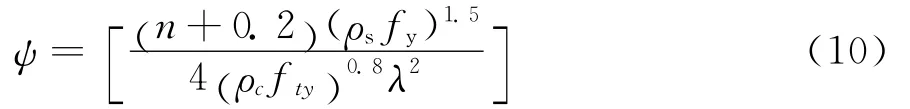
式中，fty为箍筋屈服强度。

图3 荷载修正系数kF(μΔ )与相对位移系数μΔ的关系

2.4 与试验结果的比较

试验柱荷载－变形曲线的计算结果及试验结果如图4所示。曲线1是按弯曲理论计算的荷载－弯曲变形曲线；曲线2是在曲线1基础上采用式(4)和式(5)修正后的荷载－变形曲线。由图4中的比较可知，修正后的曲线(曲线2)能较好反映柱的真实受力特性，与试验得到的骨架曲线总体吻合较好，曲线趋势基本一致。需要说明的是，图4中试件Sezen－No.1和试件Sezen－No.4的截面及各种参数基本是相同的，但二者滞回曲线的包络线相差很大，其中有很多随机因素起作用，所以准确确定包含剪切影响的构件荷载－变形特性事实上是比较困难的。

3 柱等效阻尼比计算

按能力谱方法计算结构地震下水平变形时，等效粘滞阻尼可由下式表示：

式中，ζeq为等效粘滞阻尼；ζ为结构固有的粘滞阻尼，ζ＝0.05；ζeff为滞回阻尼经计算得到的等效粘滞阻尼。

ζeff按下式计算：

图4 柱荷载－变形曲线计算结果与试验结果比较

式中，Ahs为图5中dcfgba所围的面积；Ase为最大应变能，等于图5中三角形Odh所围面积。

图5 确定等效阻尼比的滞回环

式中，ki为柱初始侧向刚度，定义为屈服点处的割线刚度；μΔ为柱侧向位移为Δd时的相对位移系数。卸载刚度ku与柱相对位移延性系数μΔ的关系如图6所示。

通过对柱试件滞回曲线的分析，卸载刚度ku可按下式计算：

图6 卸载刚度ku与柱相对位移系数μΔ的关系

图7 滞回曲线的割线刚度ke和再加载刚度kr的比较

图7为柱试验滞回曲线在不同位移反应时的割线刚度ke和反向加载刚度kr计算结果的比较，通过对二者关系的回归分析，比例系数为0.987 9，可认为滞回曲线的反向加载刚度kr与割线刚度ke相等，即：

式中，Δd为柱的侧向反应位移，Fd为与Δd对应的侧向荷载。

根据图5并联合式(11)～式(14)，得到钢筋混凝土柱等效阻尼比ζeq的计算公式如下：

4 柱抗震拟静力分析实例

4.1 抗震性能分析

图8所示为钢筋混凝土单自由度体系，上部结构的集中质量M＝105kg。柱截面尺寸为650mm×650mm；混凝土等级为C45，轴心抗压强度设计值为21.2MPa，纵筋屈服强度设计值为360MPa，极限强度为500MPa；横向钢筋屈服强度设计值为300MPa；混凝土保护层厚度为30mm；初始轴向压力为1 000kN。柱截面形式及配筋如图9所示。结构所在位置的场地类别为Ⅲ类，设计地震分组为第2组，抗震设防烈度为8度，采用罕遇地震烈度。

图8 柱计算模型

图9 柱截面形式及配筋示意图

假定柱高H＝3 250mm，在集中质量处施加水平力对柱进行推覆，该方法得到的荷载－变形曲线如图10所示。图中A点为柱的屈服点，屈服位移为0.025 58m，屈服剪力为289 543.2N；D点为假定的柱最大位移反应点。

图10 柱荷载－变形曲线

图11 A－D坐标系中的目标位移

采用中国《建筑抗震设计规范》[13](GB 50011—2010)中的地震加速度反应谱进行分析，图11示出了A－D坐标系中求得的目标位移。假定柱弹塑性层间位移角限值为1／30，而分析得到的柱层间位移角值θ＝0.097 51／3.25≈1／33.3，小于规定的限值，因而满足罕遇地震作用下8度设防的抗震要求。

4.2 抗震性能影响因素分析

下面以上述算例中的柱为“基准柱”，变化某一参数，研究其他参数对目标位移的影响。

4.2.1 剪跨比 由图12(a)可以看出，柱的水平刚度和承载力均随剪跨比的减小而提高，而延性则不断下降，说明柱由延性较好的弯曲破坏逐渐转为脆性的剪切破坏。由图12(b)可以看出，剪跨比越大，最大位移反应越大。

4.2.2 轴压比 由图13(a)可看出，随轴压比不断增大，柱荷载－变形曲线先上升后下降。由13(b)图可看出，当轴压比较小时(n＜0.2)，柱在给定地震作用下的最大位移反应随轴压比的增大而增大，表明柱在给定地震作用下的反应不断增强；轴压比继续增加(n＞0.2)，由于柱的延性降低以及荷载－变形曲线在塑性阶段下降明显，使得柱能力曲线始终位于该地震反应需求曲线之下，因而无法求得给定地震作用下的最大位移反应，即柱不能抵御该地震作用。

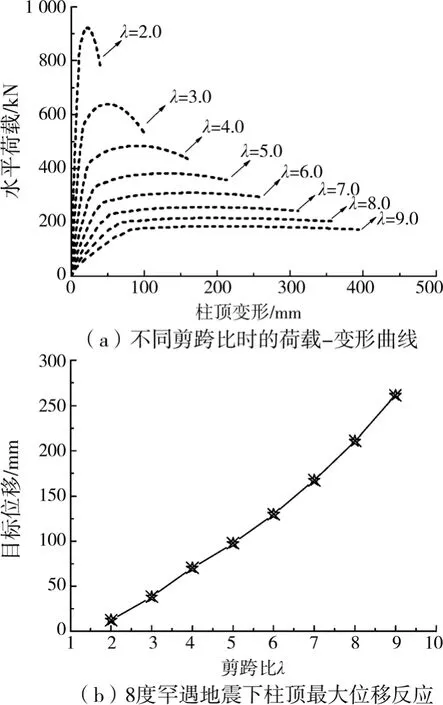
图12 剪跨比对柱抗震性能的影响

图13 轴压比对柱抗震性能的影响

4.2.3 纵筋配筋率 由图14(a)可看出，随纵筋配筋率的增加，柱的水平刚度及承载力均相应提高；进入塑性变形阶段后的荷载－变形曲线先上升后下降，并表现出较好的延性。由图14(b)可以看出，配筋率越大，柱的最大位移反应越小。

图14 纵筋配筋率对柱抗震性能的影响

4.2.4 配箍率 由图15(a)可以看出，随配箍率增加，柱的水平承载力不断提高，提高幅度呈递减趋势；而柱的屈服荷载和初始水平刚度受配箍率影响不大。柱进入塑性变形阶段后，由于剪力作用越来越明显，配箍率较小的柱的荷载－变形曲线下降迅速，且延性较差。由图15(b)中曲线的变化趋势可看出，配箍率越大，柱的最大位移反应越小，表明柱的抵御地震作用的能力越强；当配箍率增大到一定程度后，柱的地震位移反应趋于稳定，这一变化趋势与纵筋配筋率的影响相同，但地震位移反应的变化幅度与纵筋配筋率影响相比要小得多。

图15 配箍率对柱抗震性能的影响

5 结语

以钢筋混凝土偏心受压柱的弯曲特性计算为基础，结合已有的试验数据，提出了1种计算弯剪荷载－变形曲线的方法，用该方法可确定构件的“能力曲线”，并给出了弯剪构件卸载刚度与初始刚度的关系。采用该文的模型对一单自由度钢筋混凝土体系的变形性能进行Pushover分析，并分析了相关参数对柱抗震性能的影响。分析表明，剪跨比越小，柱的延性越差，进入塑性阶段的承载力下降越迅速，在地震作用下易发生剪切破坏，但剪跨比过大会降低柱的水平承载力和刚度，也会导致柱在地震作用下的变形反应超过抗震规范规定的限值；轴压比越大，柱的延性越差，柱在地震作用下的变形反应越大，不利于柱抗震，但适当增加轴压比可提高柱的水平承载力和刚度；提高纵筋配筋率和配箍率可明显改善柱的抗震性能。

[1]SETZLER E J.Modeling the Behavior of Lightly Reinforced Concrete Columns Subjected to Lateral Loads[D].Columbus：Ohio State University，2005.

[2]SEZEN H.Shear deformation model for reinforced concrete columns[J].Structural Engineering and Mechanics，2008，28(1)：39－52.

[3]SETZLER E J，SEZEN H.Model for the lateral behavior of reinforced concrete columns including shear deformations[J].Earthquake Spectra，2008，24(2)：493－511.

[4]MOSTAFAEI H，KABEYASAWA T.Axial－Shearflexure interaction approach for reinforced concrete columns[J].ACI Structural Journal，2007，104(2)：218－226.

[5]魏巍巍.钢筋混凝土结构基于修正压力场理论的承载力和变形研究[D].大连：大连理工大学，2011.

[6]ESMAEILY－GH A，XIAO Y.Seismic Behavior of Bridge Columns Ssubjected to Various Loading Patterns[R].California： Pacific Earthquake Engineering Research Center，University of California，Berkeley，2002.

[7]MANDER J B，PRIESTLEY M J N，PARK R.Theoretical stress－strain model for confined concrete.Journal of Structural Engineering，1988，114(8)：1804－1825.

[8]SAATCIOGLU M，RAZVI S R.Strength and ductility of confined concrete[J].ASCE Journal of Structural Engineering，1992，118(6)：1590－1607.

[9]YALCIN C，SAATCIOGLU M.Inelastic analysis of reinforced concrete columns [J].Computers and Structures，2000，77：539－555.

[10]赵国藩.高等钢筋混凝土结构学[M].北京：中国电力出版社，1999.

[11]PRIETLEY M J N，PARK R.Strength and ductility of concrete bridge columns under seismic loading[J].ACI Structural Journal，1987，84(8)：61－76.

[12]BERRY M，PARRISH M，EBERHARD M.PEER Structural Performance Database User's Manual(Version 1.0)[R].Berkeley：University of California，Berkeley，2004.

[13]中华人民共和国建设部.GB 50011—2010建筑抗震设计规范[S].北京：中国建筑工业出版社，2010.