长期循环荷载下饱和软黏土安定性模型

姚兆明，陈晓霞

（1．安徽理工大学 土木建筑学院，安徽 淮南232001；2．牛煤矿山建设集团有限责任公司，合肥230000；3．安阳工学院 土木建筑工程学院，河南 安阳455000）

为解释土体在长期往复荷载作用下复杂的变形机理，许多研究者在大量的室内及现场试验基础上提出许多累积变形的有效预测方法，如显式模型、套叠屈服面模型和边界面模型等。显式模型是计算地基承受长期循环荷载下变形简单实用的方法，常用的显式模型参数确定具有较大的随意性，没有明确的力学机理，计算误差较大，难以推广应用，如Li和Selig［1］、Chai等［2］，基于第一次塑性累积变形的显式模型主要参数具有明确意义且确定方便［3－4］，但显式模型计算的塑性变形随循环次数的增大一直增大，这不符合在小动应力比循环加载条件下，饱和软黏土的变形具有安定性的特点［5］。

套叠屈服面模型、边界面模型［6－7］可考虑土体复杂的循环变形特性，较为真实的反映土体变形特征，模拟效果较好，但由于采用传统的小步长积分方法，需要准确模拟每一个循环加载过程，这对于高达百万次以上往复加载计算显然是无法实现的。鉴于高频动荷载每一次循环加载产生的塑性应变相对于总应变很小及传统动态模型计算长期循环加载的实际运用上不足，一些研究者提出了基于安定性理论来计算循环加载过程中应变的累积变化规律。

Suiker［8］，Suiker和 de Borst［9］基于安定性理论并通过参考 Lemaitre和 Chaboche［10］、Peerlings等［11］和 Allou1等［12］模型中只考虑循环加载最大塑性变形包络线、计算时可采用较大的积分步长的特点提出道渣双硬化形式的安定性本构模型。张宏博等［13－14］基于经典弹塑性理论框架及结构安定理论，考虑了砂土材料的双屈服面及剪胀性特征，提出了适用于长期循环荷载作用下粉细砂累积变形计算的安定性本构模型。由于安定性模型可任意选取积分步长，能显著提高计算效率，因此非常适于实际工程的有限元计算，具有很高的应用价值［15－16］。但目前还没有一个适用于饱和软黏土大数目循环加载的累积变形计算的本构模型。

本文在构建饱和软黏土固结不排水三轴剪切总应力模型基础上，考虑软黏土在长期小动应力比循环荷载作用下具有安定性特点，结合过应力模型及安定性理论提出计算饱和软黏土长期循环荷载下轴向塑性累积应变安定性本构模型。安定性模型能合理描述饱和软黏土的循环荷载下的变形特性能，可采用任意积分步长且只考虑最大塑性变形包络线，适用于大数目循环加载的累积变形计算及承受长期循环荷载地基的有限元计算。

1 饱和软黏土循环加载安定性模型

1．1 饱和软黏土循环加载安定性理论

安定性理论较早时期一直被用来描述金属或结构在循环荷载作用下的变形特性，根据不同动应力水平，其变形特性包括4种不同响应：纯弹性、弹性安定、塑性安定及刺轮破坏，如图1。安定状态指当荷载在某个给定的范围内变化时，物体内局部区域将发生有限的塑性变形，并形成了有利的残余应力分布，在此之后，无论荷载如何变化，结构始终在稳定的残余应力状态下表现出纯弹性性质。当荷载超过一定范围之后，结构将因塑性变形的累积或塑性能量的不断耗散而破坏［14］。

图1 循环荷载作用下安定性描述

不考虑饱和软黏土饱和软黏土循环加载过程中的水压力，则安定性模型屈服函数可采用：

式中：q为循环加载偏应力水平为塑性广义剪应变；H为屈服应力，对于单调加载或比例加载情况，饱和软黏土固结不排水剪切硬化特征可由塑性功或剪切塑性累积应变来表示，为了便于研究，采用累积塑性应变作为参考变量。

由于交通荷载引起的动应力水平较低，一般无需考虑材料的动力特性及黏弹性特征，因此，可将加载过程中相关的时间参数看成为加载次数，而非实际的物理时间。因循环加载过程中每次加载产生的塑性应变很小，因此可假定安定应力在一定加载次数ΔN内保持常数，则可得此加载次数内的塑性应变增量为Δpεs，ΔN＝ΔN·Δεps。结合式（1）得：

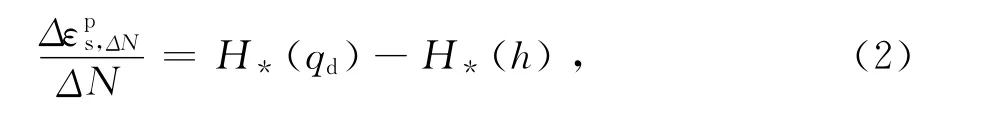
随着加载次数的增多，循环过程中塑性应变逐渐发生累积，安定应力水平也会随之逐渐提高。将式（2）对N取极限，并以h（εps）代替h得：

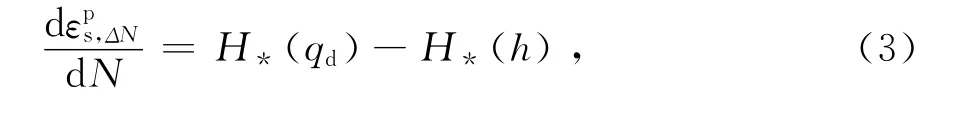
当动应力水平超过安定应力水平时，即当H＊（qd）－H＊（h（））大于0时，则将产生塑性应变。为了考虑这种关系，可将式（3）改为：

式中：＜＞为 麦考利符号。

式（4）可分别写成为（5）、（6）式：

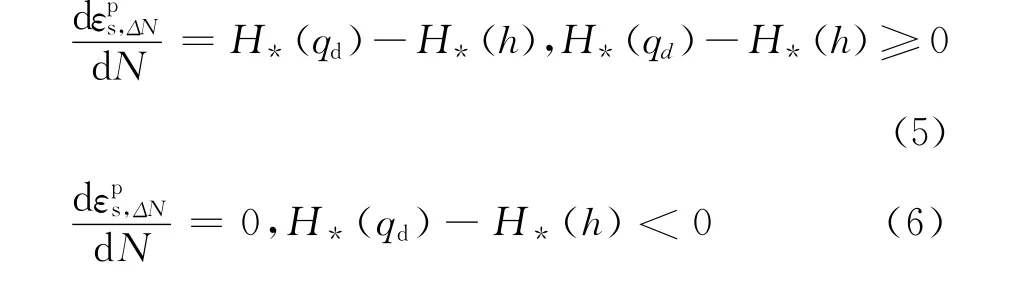
当实际应力水平超过屈服应力水平时，将会产生循环塑性变形累积，分析饱和软黏土循环加载轴向塑性累积应变结果并结合Perzyna过应力函数模型［17］，本文提出幂函数形式来描述循环荷载下饱和

式中，η、γ为模型参数，由－N曲线拟合得到，安定性应力h由饱和软黏土弹塑性模型确定。

1．2 饱和软黏土弹塑性模型

对于饱和软黏土，根据Prevost总应力模型［18］，屈服函数可表示为：

式中：q为偏应力，h为剪切屈服面的硬化参数，取塑性剪应变的函数，h＝h（）。为塑性力学中软黏土塑性累积应变率规律：定义的广义剪应变为应变偏张量，

相关流动法则采用相关联流动法，则有：

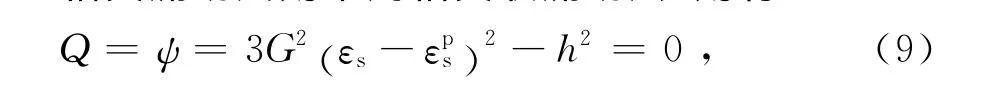
式中：G为弹性剪切模量，v泊松比，pc为初始平均有效固结压力，e为饱和软黏土固结后的孔隙比，k为弹性模量。

根据一致性条件及相关塑性流动法则得：

式中，A＝h2。

在固结不排水三轴剪切试验中，体应变为0，即ε1＋ε2＋ε3＝0，则有：εs＝ε1。即固结不排水试验中剪应变与轴向应变相等，从而得出偏应力与剪应变的增量本构关系为：

式（11）为采用Mises剪切屈服准则及相关联流动法则推导得出的固结不排水三轴条件下的应力应变本构关系。

根据饱和软黏土固结不排水剪切试验应力应变关系特点，硬化规律采用双曲线型式：

式中，qult为饱和软黏土固结不排水剪切强度，b、c为硬化规律参数，由饱和软黏土应力应变曲线关系拟合得到，pc为初始平均固结压力，pa为标准大气压力，pa＝100 k Pa。

软黏土固结不排水抗剪强度qult采用基于临界状态理论与边界面理论推导的公式来计算［15］：

式中，λ、κ分别为e－lnp空间中正常固结线和回弹线斜率，M为临界状态应力比，偏压固结下pc由初始固结压力和初始偏应力利用边界面方程计算得到［19］。

对于等向固结式（13）中α＝0，则等向固结饱和软黏土不排水抗剪强度为：

式中，p′c为初始平均固结应力。

1．3 饱和软黏土弹塑性模型验证

土样取自上海第4层淤泥质软黏土，取土深度为地下10～12 m。试样直径为39．1 mm，高为79 mm。试验在英国GDS多功能三轴仪中进行。试样物理指标为：w＝47．7%，γ＝17．8 k N／m3，Gs＝2．67，e0＝1．40，IP＝23．5。对上海第4层淤泥质软黏土分别进行σ′3c＝100、150、200 kPa偏压固结（K0＝0．7） 静力三轴固结不排水剪切试验。采用应变率为0．1 mm／min的应变控制加载方式。

饱和软黏土固结不排水临界状态比M参数由固结不排水剪切试验p′－q应力路径确定，见图2，M＝1．22。参数λ、κ分别取0．173、0．034，初始屈服面的轴线方向α＝0．625。图3为饱和软黏土固结不排水强度试验值与公式（13）、（14）计算得到的强度值，由图3可见，基于临界状态理论的饱和软黏土固结不排水计算公式能较好地计算饱和软黏土固结不排水强度值。

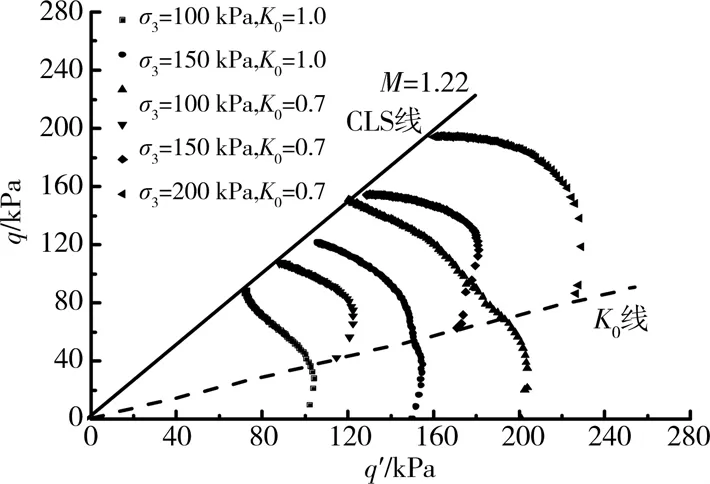
图2 固结不排水剪切应力路径

图3 固结不排水剪切强度试验值与计算值

图4中虚线和离散点分别为非等向固结不排水剪切试验应力应变模型计算曲线和试验值。由图4可见，本文的总应力模型能较好地模拟饱和软黏土固结不排水剪切试验结果。

图4 应力应变曲线

2 饱和软黏土循环荷载安定性模型验证

饱和软黏土固结不排水循环三轴试验在英国GDS多功能三轴仪中进行，分别进行σ′3c＝100 kPa、150 kPa、200 kPa偏压固结动应力比为0．06、0．1、0．2的循环加载试验，动应力比ηd定义为为动应力峰值。加载波形选用半正弦波形，加载次数均为6 000次，加载频率为1 Hz。

饱和软黏土固结不排水循环加载轴向塑性累积应变试验值见图5，图5中点表示不同循环应力比下的试验数据。对比图5中轴向循环塑性累积应变试验曲线可见，相同围压相同动应力比循环加载下，等向固结的轴向循环塑性累积应变明显大于偏压固结的轴向循环塑性累积应变，可见固结形式对轴向循环塑性累积应变影响显著。同时，在相同动应力比循环加载条件下轴向循环塑性累积应变随围压增大而增大。

安定性模型计算积分步数ΔN＝10。η、γ由Δεp1－N曲线拟合得到，b、c由本文建立的总应力模型模拟饱和软黏土固结不排水剪切试验应力应变关系得到。模型参数见表1。安定性模型计算曲线与试验曲线对比见图5，图中虚线表示模型计算结果。

表1 安定性模型参数

图5 循环累积塑性变形与循环次数关系曲线

由图5可看出轴向累积塑性应变数值模拟结果与实验结果接近，同时当循环达到一定次数时，轴向塑性累积应变达到安定值。可见，安定性模型能较好地预测饱和软黏土不排水条件循环荷载作用下轴向塑性累积应变的发展趋势，同时也能反映小动应力比循环加载下饱和软黏土轴向塑性累积应变具有安定性的特点。安定性模型计算采用计算步长为10次循环，则6 000次循环加载相当于仅进行了600次计算，大大提高了计算效率。

3 结论

1）基于过应力形式考虑最大塑性变形包络线的安定性模型可采用任意积分步长，因此具有很高的计算效率。对需进行长达数百万次循环加载有限元计算，可简化为几百次或者更少的计算次数，从而将能大大减少计算时间。

2）对于小动应力比循环加载，由于无需考虑饱和软黏土的动力特性征，从而使安定性模型用到的参数少且获取也较为方便，方便于实际工程运用。

交通荷载作用下，路基土体单元的主应力大小和方向均将发生连续变化，进一步完善主应力大小和方向连续变化的试验，进而建立更为真实反映实际应力路径的安定性模型将是以后研究的主要方向。

［1］LI D，SELIG E T．Cumulative plastic deformation for fine－grained subgrade soils［J］．Journal of Geotechnical Engineering，1996，122（12）：1006－1013．

［2］CHAI J C，MIURA N．Traffic－load induced permanent deformation of road on soft subsoil［J］．Journal of Geotechnical and Geoenvironmental Engineering，2002，128（11）：907－916．

［3］PARR G B．Some aspects of the behaviour of London clay under repeated loading［D］．UK：University of Nottingham，1972．

［4］黄茂松，李进军，李兴照．饱和软黏土的不排水循环累积变形特性［J］．岩土工程学报，2006，28（7）：891－895．HUANG MAO－SONG，LI JIN－JUN，LI XING－ZHAO．Cumulative deformation behavior of soft clay in cyclic undrained tests［J］．Chinese Journal of Geotechnical Engineering，2006，28（7）：891－895．

［5］HAMADOUCHE M A，WEICHERT D．Application of shake－down theory to soil dynamics［J］． Mechanics Research Communications，1999，26（5）：565－574．

［6］MANZARI M T，DAFALIAS Y F A．Critical state two－surface plasticity model for sands ［J］．Geotechnique，1997，47（2）：255－272．

［7］MROZ Z，NORRIS V A，ZIENKIEWICZ O C．An anisotropic hardening model for soils and its application to cyclic loading［J］．International Journal for Numerical and Analytical Methods in Geomechanics，1978，2（3）：203－221．

［8］SUIKER A S J．The mechanical behavior of ballasted railway tracks［D］．University of Delft，Delft，The Netherlands，2002．

［9］SUIKER A S J，DE BORST R．A numerical model for the cyclic deterioration of railway tracks ［J］．International Journal for Numerical Methods In Engineering，2003，57：441－470．

［10］LEMAITRE J，CHABOCHE J L．Mechanics of Solid Materials ［M ］． Cambridge University Press，Cambridge，1990．

［11］PEELINGS R H J，BREKELMANS W A M，DE BORST R，et al．Gradient－enhanced damage modeling of high－cycle fatigue［J］．Int．J．Num．Meth．Engng．2000，49：1547－1569．

［12］ALLOUL F，CHAZALLON C，HORNYCH P．A numerical model for flexible pavements rut depth evolution with time［J］．Int．J．Numer．Anal．Meth．Geomech．2007，31：1－22．

［13］张宏博，黄茂松，宋修广．循环荷载作用下粉细砂累积变形的等效黏塑性本构模型［J］．水利学报，2009，40（6）：651－658．ZHANG HONG－BO，HUANG MAO－SONG，SONG XIU－GUANG．Equivalent viscoplastic model for cumulative deformation of sandy silt under long－term cyclic loading［J］．Shuili Xuebao，2009，40（6）：651－658．

［14］张宏博．长期往复荷载作用下无黏性材料累积变形研究［D］．上海：同济大学，2006．

［15］HABIBALLAH T，CHAZALLON C．An elastoplastic model based on the shakedown concept for flexible pavements unbound granular materials［J］．International Journal for Numerical and Analytical Methods in Geomechanics，2005，29：577－596．

［16］GE Y N．Cyclic constitutive modeling of granular materials［D］．The University of Colorado，Boulder，2003．

［17］PERZYNA P．Fundamental problems in visco－plasticity［J］．Record in Advanced Applied Mechanic，1966，9：243－377．

［18］PREVOST J H．Mathematical modeling of monotonic and cyclic undrained clay behaviour［J］．International Journal for Numerical and Analytical Methods in Geomechanics，1977，1（2）：195－216．

［19］刘明，黄茂松，柳艳华．车振荷载引起的软土越江隧道长期沉降分析［J］．岩土工程学报，2009，31（11）：1703－1709．LIU MING，HUANG MAO－SONG，LIU YAN－HUA．Analysis for long－term settlement of tunnel across river induced by vehicle operation［J］．Chinese Journal of Geotechnical Engineering，2009，31（11）：1703－1709．