稳态加速度模拟试验设备：离心机设计（10）

贾普照

（北京卫星环境工程研究所，北京 100094）

本篇对离心机进行一般性理论探讨和结构设计分析，提出总体设计计算方法及总体构造与部件结构的设计建议，是离心机设计的核心部分。

本篇对离心机设计所作的分析与归纳均属首次，因此也是一次尝试，对离心机设计如果能起到提纲挈领、抛砖引玉作用，笔者就感到很欣慰了。

本篇不准备深入探讨离心机复合环境问题，包括与振动台复合及多轴载人离心机运动复合等专题性较强的内容。

本篇所提供的内容主要是作为离心机主机的一般设计计算方法，重点在于其独特的总体设计与主机机械结构部分，即其非标准设计部分；至于电气、液压、监测、控制以及机械零部件的具体设计计算，读者可从专业书籍和手册获得相应计算方法；汇电环、旋转接头、制动器、标准减速器、电动机及其驱动系统、液压传动系统、监测控制元器件等等也可获得商品供应。

在总体设计中，气动功率计算含有一定的实验与经验成分，各家有各家处理之道；总体布局与部件结构更是纷繁杂陈、琳琅满目，本文既不可能穷尽所有结构，也不会予以划一。做法是：针对不同设计理念，根据手头资料尽量展示、充分介绍，首先使资料集中呈现出来；期冀在资讯通达基础上，逐渐摸索出某种规律性的东西，因为规律本身就反映了一种认知；在阐述和分析过程中，也会直接或间接地表达笔者体会或解决办法，以供读者参考；同时，也留存了一些供读者探索与创新的空间。

为了系统观察所讨论的主题，在总体与部件结构分析时，会将有关资料予以不同的归纳与组合，不可避免地与“中篇（上）”部分内容特别是部分图片有所重复，但其担当角色各有侧重，好处是使读者在单独阅读某一章节时，能形成一个完整体系，同时免去前后翻阅之苦。

第6章 离心机力学分析及特性分析

目 录

引言

6.1 单轴转动离心机

6.1.1 单轴离心机运动学

6.1.2 单轴离心机动力学

6.2 双轴转动离心机

6.2.1 双轴离心机运动学

6.2.2 双轴离心机动态过程

6.2.2.1 双轴载人离心机的启动

6.2.2.2 座舱滚转与重力加速度

6.2.2.3 座舱滚转与切向加速度

6.2.2.4 座舱滚转与科氏加速度

6.3 三轴转动离心机

6.3.1 三轴离心机的启动

6.3.1.1 从静止启动

6.3.1.2 从1G启动

6.3.2 座舱俯仰运动

6.3.2.1 座舱俯仰运动方程

6.3.2.2 座舱俯仰角速度及角加速度

6.3.2.3 座舱俯仰过程的运动学描述

6.3.3 座舱运动与科氏加速度

6.4 离心机附加振动台

6.4.1 附加单向振动

6.4.2 附加双向振动

6.4.3 振动台对离心机的影响

6.5 离心机力学分析小结

6.6 离心机基本特性

6.6.1 离心机加速度场的不均匀性

6.6.1.1 加速度数值的不均匀性

6.6.1.2 径向加速度的辐射性

6.6.2 离心机试验的固有误差

6.6.2.1 法向加速度梯度误差

6.6.2.2 侧向加速度梯度误差

6.6.3 离心机试验的力学本质

引言

离心机是一个高速旋转的大型机械设备，当旋转同时再复合直线或其他圆周运动时，结构和分析将变得比较复杂。但不管如何复杂，其基础平台都是单自由度转动运动形式，因此我们将从基本运动形式和基础架构说起。

一般航空航天物体离心机只围绕主轴进行单自由度转动，此类离心机可称为单轴转动离心机；载人离心机则至少需具备可甩动的单轴舱，与大多数土工离心机需具有摆动式吊篮一样，呈双轴转动形态，可称为双轴转动离心机；挂有两轴常平架的载人离心机，则为三轴转动离心机；动态飞行模拟器至少有三条轴、甚至是四轴转动的形态。

在各种转动形态中，有的在吊篮或座舱内还附加了单向振动台或双向振动台等直线位移装置，呈多自由度复合运动形式。但迄今为止，从数量上说，还是单轴转动和双轴自由甩动吊篮（或座舱）的离心机最多，它们附加振动台以后，通常也不把振动位移考虑在内。因此，对单轴离心机进行基本运动分析，大致可了解绝大多数离心机的情况，同时也是研究复合转动运动的基础。

对于三轴以上的运动复合，尤其当考察点偏离几何中心，具有偏重或附加长冲程直线运动的情况，需要专题进行分析研究，本文将不涉及。

本章利用基本力学和数学分析工具，通过举例分析，重点讨论离心机典型的各种运动形式及其复合运动的简化模型，目的只是在于建立各种离心机运动的基本力学关系，探讨各类运动形态下，在力学意义上对试件、受试者及对离心机的影响等概念性问题，以便增强对离心机的整体认识与把握，熟悉离心机各运动关系间相互影响的轻重缓急与主要方面，提供进行离心机概念设计和方案设计时的基本思维与方法。如果读者对复杂离心机的运动学和动力学感兴趣，需要进行详细计算时，可利用现代设计方法与仿真计算工具再行解决。

离心机大部分的主轴都具有内孔，以供通电、通水、通气等线缆与管道穿过，结构比较粗壮，具有很好的刚性。因此，包括高加速度土工离心机在内，其最高转速也远低于其主轴临界速度。如果支撑系统也设计良好，转子系统具有足够刚性情况下，离心机在作运动分析时可以假定：

· 主轴系统为刚性转动铰，可不考虑转轴挠度及其支撑变形；

· 转子整体的变形量与其半径相比甚小，可忽略转子的变形。

因此，

· 对离心机运动学和动力学进行宏观基本分析时，可将其简化为刚体定轴转动问题；

· 而对离心机结构强度、刚度等进行微观分析时，则应按实际结构进行之。

6.1 单轴转动离心机

围绕主轴进行匀速或匀加速旋转的单轴转动状态是离心机最基本的运动状态，适用于固定吊篮物体离心机和忽略吊篮甩动过程的土工离心机，以及挂有无动力源自然甩动的单轴舱载人离心机，它们估计占有离心机总数的九成以上。

物体离心机包括土工离心机。由于限制启动的切向加速度，启动过程比较缓慢，而且吊篮在低加速度条件下很快就接近甩平，因此，这些离心机在概念设计阶段，连匀加速运动都毋庸考虑，只需为启动留有适当驱动余量，直接考察其极限状态即最高稳态运动状态即可。

只有载人离心机和动态飞行模拟器，由于其最大法向加速度和切向加速度数值比较接近，都在10g左右这样一个低数量级，试验对象又是十分重要和敏感的“人体”，才会考虑座舱甩动和切向加速度等动态因素，甚至还可能计及1g重力加速度，特别是其方向的影响。

总之，对于单轴转动离心机的研究，可以概括绝大多数离心机，也是研究一切离心机的基础。它可以利用理论力学刚体定轴转动的所有分析方法，其原理并不复杂。

6.1.1 单轴离心机运动学

作为离心机设计基础—单轴转动离心机，可采用标量法进行计算，见图6-1。

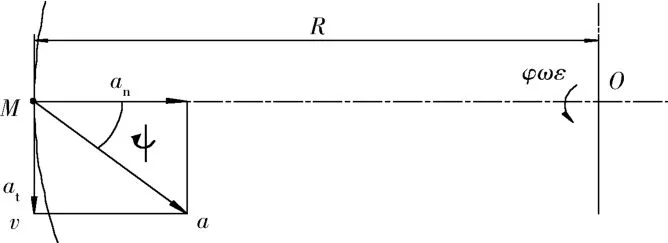
图6 -1 典型的单轴转动离心机之运动Fig.6-1 A typical single-axis rotating centrifuge

根据图6-1所示，O为离心机主轴，对离心机转子上任意点M，可建立单轴离心机运动方程（或称为主轴运动方程）如下：

对式(6-1)连续求导，可逐步得到主轴转动角速度ω（rad/s）和主轴转动角加速度ε（rad/s2）为

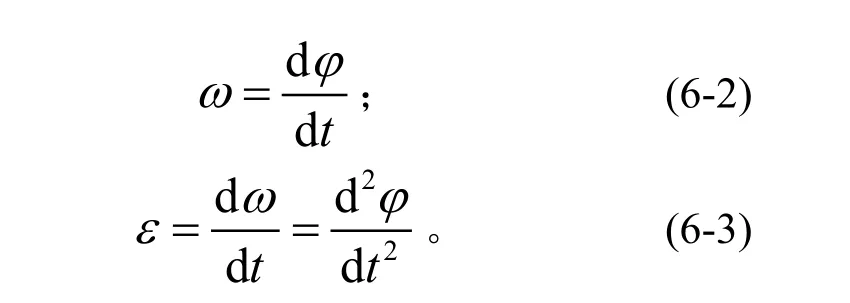
或另表达为

当ε为常数，即匀加速转动情况下，分别设φ0、ω0为t=0时的初始转角和角速度，由理论力学得

工程计算中通常以每分钟转数n（r/min）表示角速度时，它与ω（rad/s）的关系为

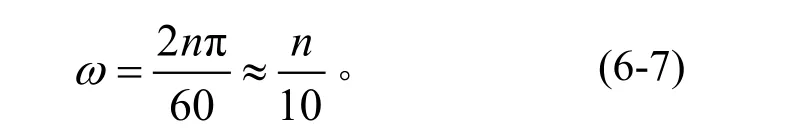
转子的角速度也就是它的转动圆频率或角频率。而转子运动周期T（s）则为

转子转动频率f（Hz）为

M点的转动线速度ν（m/s）为：

对上式求导，可得M点切向加速度（反映速度大小的变化快慢）为

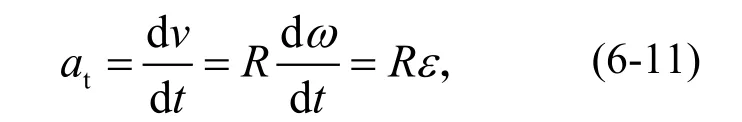
式中at的单位为m/s2。

转换公式后，得到ε（rad/s2）为

M点法向加速度（反映速度方向的变化快慢）为

式中an的单位为m/s2。

公式(6-13)经转换后，得到ω（rad/s）为

M点合成加速度为

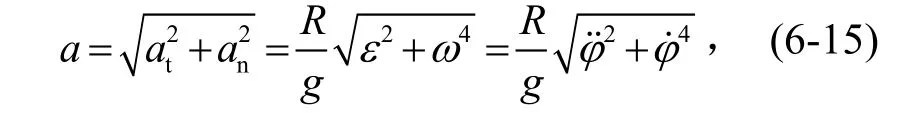
合成加速度a与半径OM的夹角ψ之正切为

在三维状态下，当离心机的合成加速度计入重力加速度时（参见图6-2），变为下式：

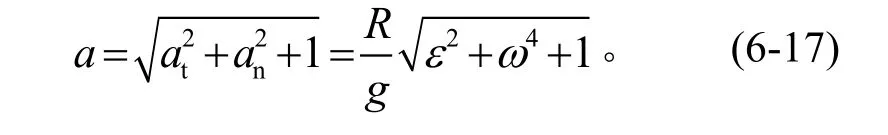
图6 -2 单轴离心机计入重力加速度的合成加速度Fig.6-2 The composite acceleration including the gravity acceleration of a single axle centrifuge

作为载人离心机和动态飞行模拟器，精确计算时可按公式(6-17)进行；对于物体离心机和土工离心机，一般按公式(6-13)或公式(6-15)直接计算向心加速度或合成加速度即可。

工程上，当已知离心机每分钟转数为n（r/min）时，法向加速度式(6-13)可转换为

关于各运动参数的方向，统一说明如下：

1）图6-2表示一系列正向和加速状态的关系：即转轴z轴向上为正，从上往下看当φ、ω、ε逆时针方向时为正（按右手规则，拇指指正向，四指自然弯曲方向为正），相应at、a、v也是正向。

2）而法向加速度an永远指向转轴中心，称之为向心加速度。

3）转动线速度永远与主轴角速度同向。当角加速度与角速度同向时，切向加速度与线速度同向，转子加速；反之减速。

6.1.2 单轴离心机动力学

相对于质点动力学基本方程，单轴离心机的质点动力学方程可表达为

在式(6-19)和式(6-20)中：Fn为法向力或离心力，N；Ft为切向力，N；m为质量，kg。

对于单轴离心机，重点是关注其法向加速度的动力学问题，它乃离心机最主要的应用价值所在。其一般物理概念为：安装于离心机上质量为 1 kg的物体，当物体旋转到法向加速度100g时，所引起的离心惯性力将使其质量力扩大100倍，相当于将1g重力场内的物体放置在100g惯性力场内，其“重量”增加了100倍一样，量纲换算如下：

相对于定轴转动动力学，当不计风阻时，可得到单轴离心机的转动微分方程为

式中：Mz为对z轴（主轴）的力矩，N·m；Jz为对z轴（主轴）的转动惯量，kg·m2；ε为角加速度，rad/s2。

由此可见，转轴力矩等于对转轴的转动惯量与角加速度的乘积（相当于直线运动时的F=ma），或转轴力矩与其角加速度成正比。

同样，我们也可得出以下一些主要表达式。

离心机转子的动能为式中T为转子动能，J 。

常用量纲换算为 1 J=1 N·m=1 kg·m2/s2。

离心机的转动功率为：

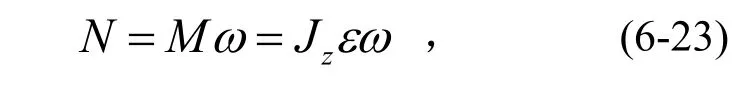
式中N的单位为W。

可见：离心机转动功率等于其力矩与角速度的乘积（相当于直线运动时P=Fv），或表示为：转动功率与角速度和角加速度的乘积成正比。

常用量纲换算为

1 W= 1 J/s=1 N·m/s=1 kg·m2/s3。当计入离心机风阻时，且已知无限空间内典型的迎风阻力为

式中：Ffz为风阻，N；C为转动体正面空气阻力系数；ρ为空气密度，ρ=1.185 kg/m3；S为转动体迎风面积，m2；v为转动体运动速度，m/s。

由式(6-24)可得到由于风阻产生的力矩为

因此，当计入风阻时的单轴离心机，其转动微分方程式变为

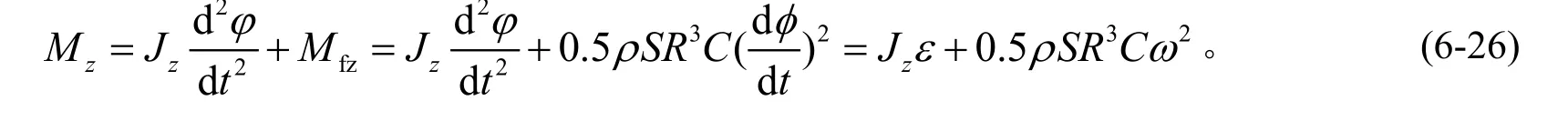
实际上，离心机处于有限空间内，如果计入气团速度，气动阻力将会减小，详细计算与分析可见第7章。

6.2 双轴转动离心机

所谓双轴转动离心机即除离心机主轴外，转臂端部增加了一根悬挂吊篮或座舱的转动轴，使吊篮或座舱随着离心机转动，靠着离心力可以自由甩动的离心机，主要指带摆动吊篮的土工离心机和单轴舱载人离心机。

双轴离心机稳态运行时的运动学分析与单轴离心机基本相同，只不过将旋转半径理解为包含吊篮或座舱甩动半径在内而已；双轴离心机动态过程主要发生在启、制动和模拟随机曲线的过程中，其中启动过程更为严酷，下面将以启动过程为例加以说明。

作为稳态加速度模拟试验设备——离心机的正常运转，当然应该以“稳”为主，因此在物体离心机和土工离心机相关试验标准中，特意规定了切向加速度的限制要求；而载人离心机恰恰相反，需要其快速启、制动以便可以进行机动飞行时的动态模拟，因此，离心机的动态分析主要针对的就是载人离心机。

单轴离心机原理简单，但双轴离心机及多轴离心机的运动分析将越来越复杂，会涉及非线性或高次高阶微分方程，有的方程不一定有解析解或简单解，就是有解也不易说明问题。为此，本节将采用MATLAB软件来图解方程或采用简算方法进行分析说明，尽量形象明确地（虽不是精确地）进行阐述。

6.2.1 双轴离心机运动学

双轴离心机运动学的分析，除与单轴离心机具有共同之处外，即主轴运动学分析外，只需补充座舱的甩动与离心机主轴间的运动关系即可。

本节分析虽然也适用于具有摆动吊篮的土工离心机，但土工离心机并不需要研究吊篮甩动过程，因此，研究重点从此已经转向载人离心机。所以，按照相应习惯，将采用重力“G”代替重力加速度“g”来表述“超重”概念。

双轴载人离心机实际上就是指单轴舱载人离心机；三轴载人离心机也就是双轴舱载人离心机。

图6-3为单轴舱载人离心机的甩动过程示意图。

图6 -3 单轴舱载人离心机自由甩动过程分析Fig.6-3 Analysis of single-axis cabin free swinging

为了有效利用离心力实现自主甩动，座舱总质心M与其摆动轴O-O'间必须有适当的偏置量r；静止状态下，座舱必然会自然下垂，甩动半径与铅垂线夹角θ=0°；这时，离心机原始转动半径R0刚好等于转臂的有效长度R'；当座舱甩起后，离心机转动半径逐渐在变长，其变化范围为：R=R'+rsinθ。

设主轴角速度和角加速度分别为ω和ε，座舱甩动角速度为ωg，根据受试者通常的原始座位，可称之为滚转角速度，质心M点的法向惯性加速度为anI，与重力加速度g的合成加速度为a。

从图中，可建立起座舱甩动的运动方程如下：

对这个非线性方程求解，不如采用举例观察图形来得直观。

设某离心机转臂有效长度为R'=7.5 m，座舱质心偏置量r=0.5 m，利用MATLAB软件可将式(6-27)绘成如下关系图（见图6-4）。

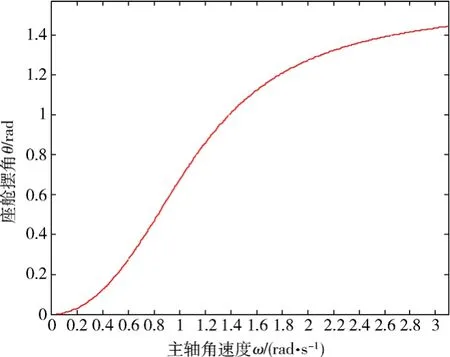
图6 -4 单轴舱载人离心机座舱摆角与主轴角速度关系Fig.6-4 Relationship between cabin tilt angle and main axle angular speed for single axle cabin centrifuge

讨论：

1）单轴舱载人离心机的座舱摆角与主轴角速度密切相关。

2）由图 6-4可见座舱摆动的规律：当离心机从静止开始启动时，一开始，座舱甩动得比较缓慢；之后，摆角则依直线增长；至某角速度以后，增长渐趋缓和，表明座舱已接近水平。因此，呈两头慢中间快的特点。

3）单轴舱载人离心机从静止或某一初始状态快速启动时，毋需 1 s，座舱就可基本甩平。在此期间，离心机旋转半径是变量，对于本例来说，半径最大变化率仅为0.5/7.5= 6.67%，意味着对径向加速度的影响也只不过是如此的比例。

4）单轴舱载人离心机受限于结构关系，座舱甩动过程中，径向加速度只与重力加速度进行合成，而数值数倍于重力加速度的切向加速度却无法参与进来；因此，加速度在数值的合成上，就已经包含了更大的误差，以后讨论会知道，其影响远远超过半径变化所引起的法向加速度误差。并且，切向加速度除数值较大以外，更重要的是方向性误差对受试者影响更为重要，而半径变化仅仅影响的只是法向加速度的些许量值而已。

5）因此，综合对受试者影响程度而言，笔者认为：一般情况下，单轴舱载人离心机进行运动学分析时，完全可以忽略半径变化这一因素，即可忽略座舱甩动过程对径向加速度的影响。

6.2.2 双轴离心机动态过程

预先说明：

1）动态过程的研究重点将放在启动过程，放在对启动加速度变化率与主轴运动参数间的关系分析上；

2）以下分析中，将忽略启动过程的半径变化量；

3）举例说明时，一律以半径R=8 m、g=9.81 m/s2、启动率为λ=6G/s的相应离心机为例。

6.2.2.1 双轴载人离心机的启动

设单轴舱载人离心机以加速度变化率λ启动。其初始合成加速度为a0、合成加速度a与加速度变化率λ的关系可表示为[1]

对于单轴舱载人离心机，限于结构原因无法计入其切向加速度，而合成加速度主要是由法向加速度和重力加速度二者所构成：

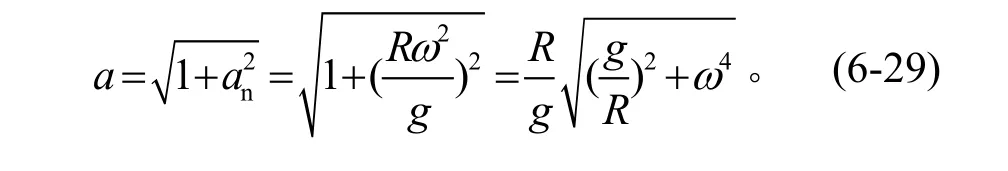
比较式(6-29)和式(6-28)，得到

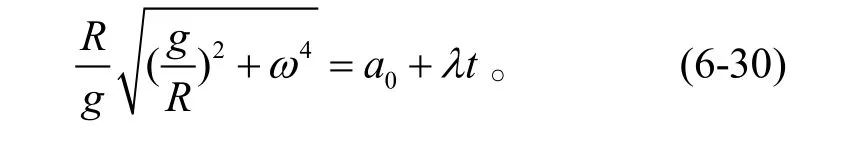
根据该式，当计入重力加速度时：

·初始合成加速度没有等于零的情况；

·当t=0，an=0，ω0=0时，初始合成加速度a0=1G，即等于重力加速度；当以λ=6G/s启动后，t=1 s时，合成加速度a=7G；

·当t=0，an=1G，ω0=ω0时，初始合成加速度a0=1.414 2G；当以λ=6G/s启动后，t=1s时，合成加速度a=7.414 2G；

·也就是说，这种情况下合成加速度始终以一个g为基础、为背景。

以下再通过举例进行具体分析。对于固定半径为8 m的单轴舱载人离心机，其合成加速度与主轴角速度的关系如图6-5所示。

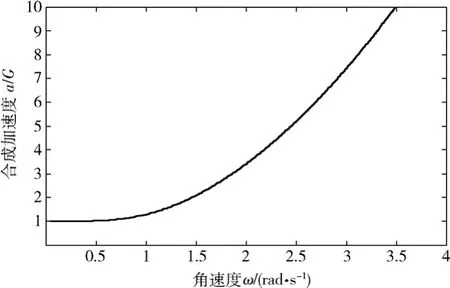
图6 -5 单轴舱载人离心机合成加速度与主轴角速度关系Fig.6-5 Single-axle cabin human centrifuge resultant acceleration versus main shaft angular speed

由图可见，随着主轴角速度增加，合成加速度以图示曲线增加，角速度为零时，合成加速度为1G。

对式(6-29)求导，得启动率表达式为

式(6-31)是一个高次二阶微分方程式。利用它求半径 8m单轴舱载人离心机从静止开始的启动过程中，启动率分别为λ=1～6G/s时，主轴角速度与角加速度的关系如图6-6所示。

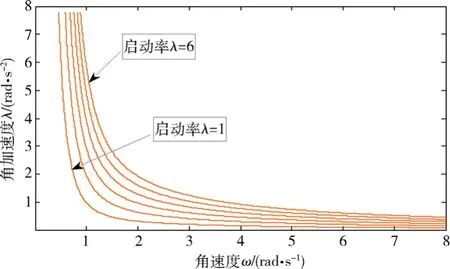
图6 -6 单轴舱载人离心机由静止启动时的主轴角速度与角加速度关系Fig.6-6 Relationship between angular velocity and angular acceleration of main axle for single-axle cabin human centrifuge startup

图6-6表明：当角速度较低时，角加速度呈开放状态。讨论：

1）单轴舱载人离心机由静止启动瞬间，当角速度为零时，需要非常大的角加速度，就是说，需要很大的驱动力矩来推动转子；

2）不论启动率大小，其规律基本一致；

3）说明，当单轴舱载人离心机以任一启动率启动情况下，一开始必然伴随着超大力矩需求，处理不当，引起冲击是完全有可能的；

4）启动后，角速度突然出现阶跃值；角速度一旦出现，角加速度迅即减小，之后呈缓慢增长趋势；

5）这就是关于载人离心机启动过程，需要建立的第一个必不可少的力学概念，即由静止直接启动离心机，需要非常大的驱动力矩。

既然如此，人们就想到从径向加速度1G启动的方法。此时，与重力加速度的合成加速度等于1.41G，按固定半径8 m计算时，其初始角速度为

图6-7表示的就是从1.41G启动的情况，即以ω0=1.107 4 rad/s启动。可见：

1）启动瞬间，角加速度已出现有限值，表明启动过程所需力矩大为减小，冲击缓和；

2）随着启动率变小，冲击愈趋减小；

3）角速度由零逐渐增加；

4）其余情况与前基本相同。

图6 -7 单轴舱载人离心机由1.41 G启动时的主轴角速度与角加速度关系Fig.6-7 Relationship between angular velocity and angular acceleration of main axle for single-axle cabin human centrifuge starting from 1.41 G

将式(6-31)转化为下式：

式(6-32)通过MATLAB数值求解，可得到单轴舱载人离心机从静止以λ=6G/s启动时的角位移与角速度的变化情况（参见图6-8）。

图6-8表明：在时刻为零、静止状态时，角速度已有一个跳跃。如前所述，即需要大的角加速度介入。

图6 -8 单轴舱载人离心机由静止启动的转角与角速度Fig.6-8 Single axle cabin human centrifuge’s rotational angle and angular velocity startup from rest

该曲线启动1 s附近时的具体数据如表6-1所示。

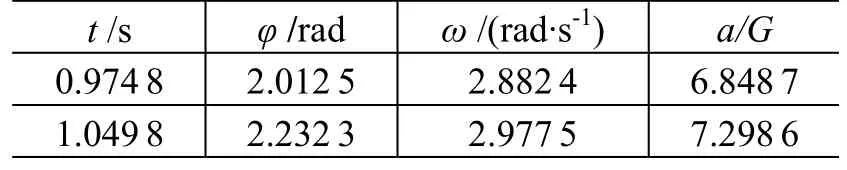
表6 -1 单轴离心机从静止启动1 s左右的数据Table 6-1 Single axle cabin human centrifuge’s start data about one second startup from the static

可见，1 s时的合成加速度当为7G。图6-9表示了由1.41G与由静止状态，均以λ=6G/s启动时的比较图。

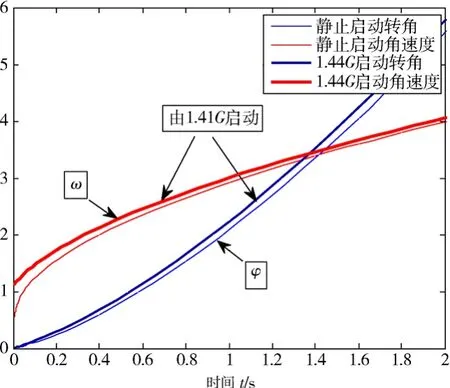
图6 -9 单轴舱载人离心机由静止和1.41 G启动比较Fig.6-9 Single axle cabin human centrifuge startup from rest and from 1.41 G

启动1 s左右时的数据如表6-2所示：

表6 -2 单轴离心机从静止启动1.41 G左右的数据Table 6-2 Single axle cabin human centrifuge’s start data about one second startup from 1.41 G

可见，1 s时的合成加速度约为7.41G。

讨论：

1）由1.41G启动，其初始角速度基本上已相当于静止启动时的平稳增长段，躲过了超高角加速度出现的极端情况，所需角加速度大为减少；

2）由1.41G启动，除启动瞬间角加速度有一点冲击之外，其余曲线段都比较平稳；

3）由1.41G启动，可消除机械传动系统的齿隙和静、动态摩擦状态转换时的非线性过程；

4）因此，从1.41G启动，无疑是载人离心机最好的启动方式。

（未完待续）

（Reference）

[1]Drone K C.Design study for an acceleration research device, AD 268621[R], 1961